16.2 ARITHMETIC OPERATIONS

First analyze the main arithmetic operations and generate the corresponding computation algorithms.

16.2.1 Addition of Positive Numbers

Given two positive floating-point numbers s₁.B^e1 and s₂.B^e2 their sum s.B^e is computed as follows.

Assume that e₁ is greater than or equal to e₂; then (alignment) the sum of s₁.B^e1 and s₂.B^e2 can be expressed in the form s.B^e, where

The value of s belongs to the interval

so that s could be greater than or equal to B. If it is the case, that is, if

then (normalization) substitute s by s/B, and e by e + 1, so that the value of s.B^e is the same as before, and the new value of s satisfies

The significands s₁ and s₂ of the operands are multiples of ulp. If e₁ is greater than e₂, the value of s could no longer be a multiple of ulp and some rounding function should be applied to s. Assume that

s′ and s″ being two successive multiples of ulp. Then the rounding function associates to s either s′ or s″, according to some rounding strategy. According to (16.9) and to the fact that 1 and B − ulp are multiples of ulp, it is obvious that

Nevertheless, if condition (16.8) does not hold, that is, if

s could belong to the interval

so that rounding(s) could be equal to B. A new normalization step would be necessary, that is, substitution of s = B by s = 1 and e by e + 1.

Algorithm 16.1 Sum of Positive Numbers

if e1>=e2 then e:=e1; s:=s1+(s2/B*(e1-e2));
else e:=e2; s:=(s1/B*(e2-e1))+s2; end if;
if s>=B then e:=e+1; s:=s/B; end if;
s:=round(s);
if s>=B then e:=e+1; s:=s/B; end if;

Examples 16.2 Assume that B = 10 and ulp = 10⁻⁴, so that the numbers are represented in the form s.10^e where 1 ≤ s ≤ 9.9999.

1. Compute z = (3.4375 × 10³) + (2.5491 × 10⁻¹):

2. Compute z = (9.4375 × 10³) + (8.6247 × 10²):

3. Compute z = (9.4375 × 10³) + (5.6247 × 10²):

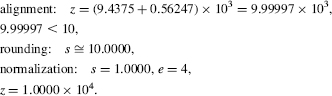
Comment 16.1 The addition of two positive numbers could produce an overflow, as the final value of e could be greater than e_max.

16.2.2 Difference of Positive Numbers

Given two positive floating-point numbers s₁.B^e1 and s₂.B^e2 their difference s.B^e is computed as follows:

Assume that e₁ is greater than or equal to e₂; then (alignment) the difference between s₁.B^e1 and s₂.B^e2 can be expressed in the form s.B^e, where

The value of s belongs to the interval

If s is negative, then it is substituted by –s and the sign of the final result will be modified accordingly. If s is equal to 0, an exception equal_zero could be raised. It remains to consider the case where

The value of s could be smaller than 1. In order to normalize the significand, a procedure

procedure leading_zeroes(s: in fixed_point; k: out natural)

must be executed: it counts the number of initial 0′s of the representation of s. In other words, it looks for the minimum exponent k such that s.B^k ≥ 1. Then s is substituted by s.B^k and e by e − k. Thus, the relation (16.10) holds, that is,

It remains to round (up or down) the significand and to normalize it if necessary.

Algorithm 16.2 Difference of Positive Numbers

if e1>=e2 then e:=e1; s:=s1-(s2/B**(e1-e2));
else e:=e2; s:=(s1/B**(e2-e1))-s2; end if;
if s<0 then s:=-s; sign:=1; end if;
leading_zeroes(s, k);
s:=s*(B**k); e:=e-k;
s:=round(s);
if s>=B then e:=e+1; s:=s/B; end if;

Examples 16.3 Assume again that B = 10 and ulp = 10⁻⁴, so that the numbers are represented in the form s.10^e where 1 ≤ s ≤ 9.9999. For computing the difference, the 10's complement system is used.

1. Compute z = (3.4518 × 10⁻¹) − (7.2471 × 10³):

2. Compute z = (1.0014 × 10³) − (9.9491 × 10²):

3. Compute z = (1.0714 × 10⁴) − (7.1403 × 10²):

Comment 16.2 The difference of two positive numbers could produce an underflow, as the final value of e could be smaller than e_min.

16.2.3 Addition and Subtraction

Given two floating-point numbers (−1)^sign1.s₁.B^e1 and (−1)^sign2.s₂.B^e2, and a control variable operation, an algorithm is defined for computing

TABLE 16.1

Once the significands have been aligned, the actual operation (addition or subtraction of the significands) depends on the values of operation, sign₁, and sign₂ (Table 16.1).

The following algorithm, based on Algorithms 16.1 and 16.2 as well as Table 16.1, computes z.

Algorithm 16.3 Addition and Subtraction

if e1>=e2 then e:=e1; s2:=s2/B**(e1-e2);
else e:=e2; s1:=s1/B**(e2-e1); end if;
sign:=sign1;
if operation xor sign1 xor sign2=0 then
  s:=s1+s2;
  if s>=B then e:=e+1; s:=s/B; end if;
  s:=round(s);
  if s>=B then e:=e+1; s:=s/B; end if;
else
  s:=s1-s2;
  if s<0 then s:=-s; sign:=1-sign; end if;
  leading_zeroes(s, k);
  s:=s*(B**k); e:=e-k;
  s:=round(s);
 if s>=B then e:=e+1; s:=s/B; end if;
end if;

As regards the hardware implementation, the following equivalent algorithm is better.

Algorithm 16.4 Addition and Subtraction, Second Version

if operation=1 then sign2:=1-sign2; end if;
if e1<e2 then swap(sign1, sign2); swap(s1, s2); swap (e1, e2);
end if;
e:=e1; s2:=s2/B**(e1-e2); sign:=sign1;
if sign xor sign2=0 then
 s:=s1+s2;
 if s>=B then e:=e+1; s:=s/B; end if;
else
 if (e1=e2) and (s1<s2) then swap(s1, s2); sign:=1-sign;
 end if;
 s:=s1-s2;
 leading_zeroes(s, k);
 s:=s*(B**k); e:=e-k;
end if;
s:=round(s);
if s>=B then e:=e+1; s:=s/B; end if;

16.2.4 Multiplication

Given two floating-point numbers (−1)^sign1.s₁.B^e1 and (−1)^sign2.s₂.B^e2, their product (−1)^sign.s.B^e is computed as follows:

The value of s belongs to the interval

and could be greater than or equal to B. If it is the case, that is, if

then (normalization) substitute s by s/B, and e by e + 1. The new value of s satisfies

(ulp < B so that 2 − ulp/B > 1).

It remains to round the significand and to normalize if necessary.

Algorithm 16.5 Multiplication

sign:=sign1 xor sign2; s:=s1*s2; e:=e1+e2;
if s>=B then e:=e+1; s:=s/B; end if;
s:=round(s);
if s>=B then e:=e+1; s:=s/B; end if;

Examples 16.4 Assume that B = 10 and ulp = 10⁻⁴, so that the numbers are represented in the form s.10^e, where 1 ≤ s ≤ 9.9999.

1. Compute z = (3.4382 × 10³)×(2.5471 × 10⁻¹):

2. Compute z = (9.4300 × 10³)×(8.6200 × 10²):

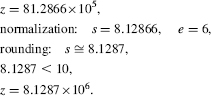
3. Compute z = (4.7619 × 10²)×(2.1000 × 10³):

Comment 16.3 The product of two real numbers could produce an overflow as the final value of e could be greater than e_max.

16.2.5 Division

Given two floating-point numbers (−1)^sign1.s₁.B^e1 and (−1)^sign2.s₂.B^e2 their quotient (−1)^sign.s.B^e is computed as follows:

The value of s belongs to the interval

and could be smaller than 1. If that is the case, that is if s = s₁/s₂ < 1, then

and

Then (normalization) substitute s by s.B, and e by e − 1. The new value of s satisfies

It remains to round the significand.

Algorithm 16.6 Division

sign:=sign1 xor sign2; s:=s1/s2; e:=e1 – e2;
if s<1 then e:=e–1; s:=s*B; end if;
s:=round(s);

Examples 16.5 Assume that B = 10 and ulp = 10⁻⁴, so that the numbers are represented in the form s.10^e, where 1 ≤ s ≤ 9.9999.

1. Compute z = (3.4375 × 10³)/(2.5491 × 10⁻¹):

2. Compute z = (2.5491 × 10⁻¹)/(3.4375 × 10³):

Comment 16.4 The quotient of two real numbers could produce an underflow, as the final value of e could be smaller than e_min.

16.2.6 Square Root

Given a positive floating-point number s₁.B^e1, its square root s.B^e is computed as follows:

In the first case (16.22),

In the second case (16.23),

and (normalization) s must be substituted by s.B and e by e – 1, so that

It remains to round the significand and to normalize if necessary.

Algorithm 16.7 Square Root

if (e1 mod 2)=1 then s1:=s1/B; e1:=e1+1; end if;
s:=square_root(s1); e:=e1/2;
if s<1 then e:=e-1; s:=s*B; end if;
s:=round(s);
if s>=B then e:=e+1; s:=s/B; end if;

Examples 16.6 Assume that B = 10 and ulp = 10⁻⁴, so that the numbers are represented in the form s.10^e, where 1 ≤ s ≤ 9.9999.

1. Compute z = (9.9491 × 10²)^1/2:

2. Compute z = (3.4518×10⁻¹)^1/2:

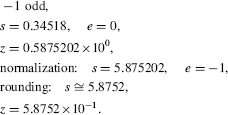
3. Compute z = (9.9999 × 10³)^1/2:

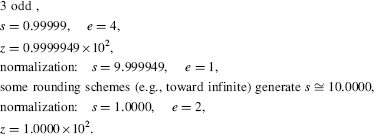
Comments 16.5 The square rooting of a real number could produce an underflow, as the final value of e could be smaller than e_min.