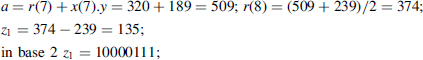8.1 OPERATIONS IN Z_m

Given a natural number m > 1, the set Z_m = {0, 1, … , m − 1} is a ring whose operations are defined modulo m (Chapter 2):

8.1.1 Addition

Given two natural numbers x and y belonging to the interval 0 ≤ x, y < m, compute z = (x + y) mod m. Taking into account that

z must be equal to either x + y or x + y − m. The corresponding algorithm is the following.

Algorithm 8.1 Modulo m Addition

z1:=x+y; z2:=z1 − m;
if z2>=0 then z:=z2; else z:=z1; end if;

Assume now that Bⁿ⁻¹ < m ≤ Bⁿ and that x and y are n-digit base-B numbers. Consider three cases:

So Algorithm 8.1 can be substituted by the following one where all operands have n digits.

Algorithm 8.2 Base B Modulo m Addition

z1:=(x+y) mod B**n; c1:=(x+y)/B**n;
z2:=(z1+B**n - m) mod B**n; c2:=(z1+B**n - m)/B**n;
if c1=0 and c2=0 then z:=z1; else z:=z2; end if;

Example 8.1 Assume that B = 10, n = 3, m = 750, so that Bⁿ − m = 250:

8.1.2 Subtraction

Given two natural numbers x and y belonging to the interval 0 ≤ x, y < m, compute z = (x − y) mod m. Taking into account that

z must be equal to either x − y or x − y + m. The corresponding algorithm is the following.

Algorithm 8.3 Modulo m Subtraction

z1:=x − y; z2:=z1+m;
if z1<0 then z:=z2; else z:=z1; end if;

If Bⁿ⁻¹ < m ≤ Bⁿ, and x and y are n-digit base-B numbers, consider two cases:

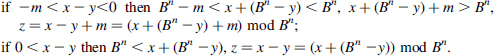
Algorithm 8.3 can be substituted by the following algorithm where all operands have n digits.

Algorithm 8.4 Base B Modulo m Subtraction

z1:=(x+B**n − y) mod B**n; c1:=(x+B**n − y)/B**n;
z2:=(z1+m) mod B**n;
if c1=1 then z:=z1; else z:=z2; end if;

Example 8.2 Assume that B = 10, n = 3, m = 750:

8.1.3 Multiplication

Given x and compute z = x.y mod m. Assume that x, y, and m are represented in base B and that m < Bⁿ (if m = Bⁿ the modulo m reduction is trivial).

8.1.3.1 Multiply and Reduce

The first algorithm consists of (1) multiplying x by y, obtaining a 2.n-digit intermediate result p, and (2) reducing p modulo m. The following multiplication and division procedures must have been defined:

procedure multiply (x, y: in digit_vector (0..n−1); z: out
digit_vector (0..2*n−1));

procedure divide (x: in digit_vector (0..2*n−1); y: in
digit_vector (0..n−1); q: out digit_vector (0..n−1); r:
out digit_vector (0..n−1));

Given two natural numbers x and y, the first procedure generates the product z = x.y, and the second one the quotient q and the remainder r such that x = q.y + r, with r < y. For that purpose any one of the multiplication (Chapter 5) and division (Chapter 6) algorithms can be used. The following algorithm is based on the property:

z = x.y mod m if, and only if, z < m and there exists a natural number q such that x.y = q.m + z.

Algorithm 8.5 Base B Modulo m Multiplication, Multiply and Reduce

multiply (x, y, p);
divide (p, m, q, z);

8.1.3.2 Modified Shift-and-Add Algorithm

An alternative solution consists of using Algorithm 5.1 and reducing modulo m in every step.

Algorithm 8.6 Modulo m Shift-and-Add Algorithm

p(n):=0;
for i in 0..n−1 loop
   p(n−1-i):=(p(n-i)*B+x(n−1-i)*y) mod m;
end loop;
z:=p(0);

Assume now that Bⁿ⁻¹ < m ≤ Bⁿ and that x and y are n-digit base-B numbers. Observe that

so that p(n − i).B + x(n − 1 − i).y is an (n + 2)-digit number and

where

is a 2-digit number. In order to execute Algorithm 8.6, two procedures must be defined: the first one computes x.B + a.y, where x and y are n-digit numbers and a is a digit:

procedure shift_and_add (x, y: in digit_vector (0..n−1); a: in
digit; z: out digit_vector(0..n+1));

the second one is a division procedure:

procedure divide (x: in digit_vector (0..n+1); y: in digit_
vector (0..n−1); q: out digit_vector (0..1); r: out
digit_vector (0..n−1));

Algorithm 8.6 can be substituted by the following algorithm where all operands have n digits:

Algorithm 8.7 Base-B Modulo m Shift-and-Add Algorithm

p(n):=0;
for i in 0..n−1 loop
   shift_and_add (p(n-i), y, x(n−1-i), z1);
   divide (z1, m, q, p(n−1-i));
end loop;
z:=p(0);

In base B = 2 the execution of the main operation of Algorithm 8.6, namely,

can be performed in a slightly different way. According to (8.2) and (8.3)

where q < 3, so that q is either 0, 1, or 2.

Algorithm 8.8

p1:=p(n-i)*2; p2:=p1+x(n-i−1)*y-m;
if p2<0 then p3:=p2+m; p(n−1-i):=p3;
else
  p3:=p2-m;
  if p3<0 then p(n−1-i):=p2; else p(n−1-i):=p3; end if;
end if;

Algorithm 8.8 can be simplified. On the one hand p2 and p3 cannot be simultaneously negative:

so that −m ≤ p2 < 2.m; if p2<0 then p3 = p2 + m ≥ − m + m = 0. On the other hand, instead of computing

the value of k = m − y can be precalculated (outside the main loop) so that p2 is equal to either p1 − m if x(n − i − 1) = 0 or p1 − k = p1 − m +y if x(n − i − 1) = 1. The modified algorithm is the following.

Algorithm 8.9 Base-2 Modulo m Shift-and-Add Algorithm

p(n):=0; k:=m-y;
for i in 0..n−1 loop
  if x(n-i-1)=0 then w:=m; else w:=k; end if;
  p1:=p(n-i)*2; p2:=p1-w;
  if p2<0 then p3:=p2+m; else p3:=p2-m; end if;
  if p3<0 then p(n−1-i):=p2; else p(n−1-i):=p3; end if;
end loop;
z:=p(0);

8.1.3.3 Montgomery Multiplication

In some cases the use of the Montgomery product concept ([MON1985]) allows one to reduce the computation complexity. Only the binary case (B=2) will be studied. The corresponding algorithm is based on the fact that, given three n-bit natural numbers x, y, and m, such that

it is relatively easy to find a natural number z < m such that

As m is an odd number, the greatest common divisor of 2ⁿ and m is 1, so that there exits a natural number, denoted 2⁻ⁿ, such that 2⁻ⁿ. 2ⁿ = 1 mod m, and the preceding relation can be written in the form

Relation (8.5) defines the Montgomery product of x by y. The following algorithm computes z.

Algorithm 8.10 Montgomery Product

r(0):=0;
for i in 1..n loop
   a:=r(i−1)+x(i−1)*y;
   r(i):=(a+a(0)*m)/2;
end loop;
if r(n)<m then z:=r(n);
else z:=r(n)-m; end if;

It is based on the following lemmas.

Lemma 8.1

Proof First observe that if m is odd (m(0)= 1) then at each step a + a(0).m is even:

Then the property is demonstrated by induction. At the first execution of the iteration,

At step number i,

Lemma 8.2

Proof The property is demonstrated by induction. At the first execution of the iteration,

At step number i,

A direct consequence of Lemmas 8.1 and 8.2 is that

so that z is either r(n) or r(n) − m.

Assume that the procedure Montgomery_product has been defined:

procedure Montgomery_product (x, y, m: in bit_vector
(0..n − 1); z: out bit_vector (0..n − 1));

and that the value of

has been previously computed. Then z = x.y mod m can be computed as follows:

Algorithm 8.11 Modular Product Based on the Montgomery Product

Montgomery_product (x, y, m, z1);
Montgomery_product (z1, exp_2n, m, z);

Example 8.3 n = 8, m = 239, x = 217, y = 189; in base 2, x = 11011001; exp_2n = 2¹⁶ mod 239 = 50.

First compute the Montgomery product of x and y:

then compute the Montgomery product of z₁ and exp_2n:

conclusion: 217 × 189 mod 239 = 144.

In the case of multioperand modular products an elegant presentation—not always an effective one—is based on the definition of a mapping T from Z_m into Z_m:

Use the following notation for representing the Montgomery product:

Then the following properties are evident:

∀ x and y in Z_m.

According to (8.11), the transformation T replaces the mod m product by the Montgomery product. The following algorithm computes the product

Algorithm 8.12 Multioperand Modular Product Based on the Montgomery Product

for i in 1..k loop Montgomery_product(x(i), exp_2n, m,
y(i)); end loop;
p(1):=y(1);
for i in 2..k loop Montgomery_product(p(i−1), y(i), m,
p(i)); end loop;
z:=Montgomery_product(p(k), 1, m, z);

The preceding algorithm includes 2.k Montgomery products, instead of k modular products if a classical multioperand product algorithm were used. Generally, the shorter computation time of the Montgomery product does not compensate the multiplication by 2 of the number of primitive operations. This drawback disappears if many operands are known to be identical, as is the case if an exponential function such as x^k is computed (Section 8.1.4).

8.1.3.4 Specific Ring

In the preceding algorithms m is a parameter whose value is any natural number greater than 1. For some particular values of m, specific algorithms can be defined. As an example, if m = B^k − c for some small c, the modulo m reduction is easier. Assume that x is a 2.n-digit number (the product of two n-digit numbers) and m = Bⁿ − c, with c Bⁿ. Then x can be decomposed in the form x = x₁.Bⁿ + x₀, with x₁ and x₀ smaller than Bⁿ, so that

where

So instead of reducing x modulo m, the first operation consists of computing x′, and then reducing x′. If x′ is still greater than Bⁿ, the same transformation can be performed, that is, and so on. Eventually a number z is obtained such that z < Bⁿ and x mod m = z mod m.

Algorithm 8.13 Modulo m Reduction

z:=x;
while z>=B**n loop
  z1:=z/B**n; z0:=z mod B**n; z:=z1*c+z0;
end loop;
z:=z mod m;

In base B = 2, with m ≥ 2ⁿ⁻¹, the last instruction is replaced by

if z >=m then z:=z−m; end if;

Example 8.4

B = 2, n = 8, m = 239, x = 217, y = 189;

In order to compute z = x.y mod 239, first compute p = x.y = 41013; then reduce p mod 239 = 2⁸ − 17:

Even more specific algorithms can be used.

Example 8.5 Assume again that B = 2, n = 8, m = 239 = 2⁸ − 17 and that x is a 2.n-bit number. The computation of x mod 239 can be performed as follows:

If x = 41013 then

8.1.4 Exponentiation

Given x and compute e = y^x mod m. Assume that x, y, and m are represented in base 2 and that m < 2ⁿ. Then

and e can be written in the form (a so-called Horner scheme)

The corresponding algorithm is the following.

Algorithm 8.14

e:=1;
for i in 1..n loop
   e:=(e*e) mod m;
   if x(n-i)=1 then e:=(e*y) mod m; end if;
end loop;

This algorithm includes a lot of mod m products. Nevertheless, all the operands are either 1, y, or a previously obtained value (e), so that an alternative solution is the use of the Montgomery product (Section 8.1.3.3, relations (8.7) to (8.11)). The computation is performed as follows:

1. Substitute the initial operands 1 and y by T(1) = 2ⁿ mod m and T(y) = MP(y, exp_2n).
2. Execute the main loop of Algorithm 8.14 substituting the mod m products by Montgomery products.
3. Compute T⁻¹(e) = MP(e, 1).

Assume that exp_n = 2ⁿ mod m and exp_2n = 2²ⁿ mod m have been previously computed. The following algorithm computes e = y^x mod m:

Algorithm 8.15

e_transformed:=exp_n;
Montgomery_product (y, exp_2n, m, y_transformed);
for i in 1..n loop
   Montgomery product (e_transformed, e_transformed, m,
   e_transformed);
   if x(n-i)=1 then
   Montgomery_product (e_transformed, y_transformed, m,
   e_transformed); end if;
end loop;
Montgomery_product (e_transformed, 1, m, z);