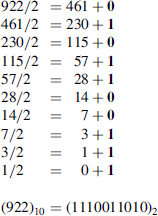7.1 BASE CONVERSION

Given the representation of a number in a specific system, conversion operations consist of finding the representation of this number in another system. Arithmetic algorithms deal with a diversity of systems such as base-B for naturals or signed systems for integers; the most common signed systems are sign-magnitude, B's complement, excess-k, or signed-digit systems such as Booth coding. Finally, special attention is paid to floating-point representations for computer applications. Redundant systems are also important in arithmetic operations, among others in multiplication (Booth algorithm, Chapter 5) or division (SRT, Chapter 6). Booth coding and redundant base-B coding are generally related to specific algorithms; the conversion techniques are therefore developed in the sections devoted to the respective algorithms. Floating-point conversion is reviewed in Chapter 16. The most classic problem to deal with is the base conversion for base-B unsigned representations: given a number by its representation in base B₁, find its corresponding representation in base B₂.

Let the base-B₁ (source system) representation of a natural number x be given by

weighted sum of powers of B. The problem at hand is to compute the base-B₂ (target system) representation of x

A first simple solution consists of computing (7.1) in the target system. Expression (7.1) may be written under the Hörner form (Chapter 5) as

then iteratively computed in base B₂. The following algorithm generates the value of x in base-B₂ from its base-B₁ representation (x_n−1, x_n−2, … , x₀):

acc:=0; for i in 0..n−1 loop acc:=acc*B1+x(n − 1 − i);
end loop; x:=acc;

In order to generate the base-B₂ representation of x, the preceding algorithm is executed in base B₂. The base-B₂ representation of acc.B₁ + x_n−1−i is generated by the following set of integer divisions:

where acc_i is the digit i of acc expressed in base B₂.

From the preceding system the following equality is deduced:

Choose the value of m in such a way that . In the last equality q_m = 0. The following algorithm executes the assignation acc:=acc.B₁ + x_n−1−i in base B₂:

q:=x(n−1−i);
for j in 0..m−1 loop q:=(acc(j)*B1+q)/B2;
  acc(j):=(acc(j)*B1+q) mod B2; end loop;

The complete conversion algorithm is then given as follows:

Algorithm 7.1 Base Conversion Algorithm

-acc:=0;
for j in 0..m-1 loop acc(j):=0; end loop;
for i in 0..n−1 loop
      --acc:=acc*B1+x(n−1−i);
      q:=x(n−1-i);
      for j in 0..m−1 loop q:=(acc(j)*B1+q)/B2;
        acc(j):=(acc(j)*B1+q) mod B2; end loop;
end loop;
--x:=acc;
for j in 0..m−1 loop x(j):=acc(j); end loop;

The basic computation primitive calculates

where

Examples 7.1

1. Compute the hexadecimal representation of the decimal number (9128)₁₀. Observing that 16³ < 10⁴ < 16⁴, one selects m = 4.
2. Compute the decimal representation of the hexadecimal number (23A8)₁₆. Observing that 10⁴ < 16⁴ < 10⁵, one should select m = 5; actually, m = 4 is sufficient for this particular case so m = 4 is selected to reduce the number of useful steps.

Problem 2 is the back-conversion of the result of problem 1; both examples are presented in parallel columns of the following table.

Decimal-to-binary and binary-to-decimal conversions may readily be handled by Algorithm 7.1. According to the prominent role of those particular cases in digital system implementations, special attention has been given to them in the literature. Basically three methods are more commonly described for decimal-to-binary conversion. The first one consists of subtracting from the successive remainders R the greatest power of 2 (2^p) inferior or equal to R. Successive exponents p identify the bit-1 positions of the desired binary expression. Step i of a nonrestoring version of this algorithm would add or subtract 2^(n−1−i) according to the sign of the preceding remainder: adding 2^(n−1−i) to a negative remainder and conversely. The second method consists of computing the remainders (parity) of the integer division by 2 of the successive decimal quotients, starting from the decimal number to be converted. The third method is the adaptation of Algorithm 7.1. At the implementation level, the complexity would depend on the form decimal digits are provided. Decimal numbers are generally assumed represented in BCD form (binary coded decimal, Chapter 3). Then algorithms are implemented as a sequence of binary operations. A close look at Example 7.2(3) shows that the first step of the third method (Algorithm 7.2) actually sets the leftmost decimal digit to BCD; so this step can be skipped if the decimal number to convert is already BCD coded. In this algorithm, the successive steps iteratively perform the multiplication of the intermediate result (stored in acc) by the base (10)₁₀ = (1010)₂, and then add the next (binary coded) decimal digit. Let us point out moreover that multiplying a number N by (1010)₂ can readily be implemented as 2.N + 8.N or 2.(N + 4.N), that is, a simple 1-shifted(N + 2-shiftedN) operation. Assuming m and n to be the number of digits of the decimal and binary representations, respectively, the time complexity (in number of steps) of the first two methods is n while the third one is m. The step complexity has to be evaluated in the context of the implementation resources. The BCD-to-binary conversion algorithm can be stated as follows.

Algorithm 7.2 BCD-to-Binary Conversion Algorithm

Examples 7.2 Convert in binary (922)₁₀

1. Nonrestoring 2^p subtracting.

   

2. Division-by-2.

   

3. Algorithm 7.2.

   

The most intuitive method to achieve a binary-to-decimal conversion is to compute the decimal representations of the relevant powers of 2, and then add them together. This corresponds to the decimal computation of the expression Σ_ix_i.2ⁱ. An algorithm consisting of computing the remainders of successive divisions by ten doesn't appear easy to implement. Algorithm 7.1 looks the most attractive as it still reduces to a straight application of the Hörner expansion (7.3). Assuming that a BCD representation is desired for the converted result, the binary-to-BCD algorithmic step performs the multiplication of the intermediate result (stored in acc) by the base 2 = (10)₂, and then adds the next bit. For this purpose, define a procedure to multiply a BCD number by 2 (BCDx2 procedure). Note that a shifted (multiplied by 2) 4-bit binary number can be coded in BCD form applying the following simple rules:

Observe that the x2 operation on a single BCD digit leaves y(i)₀ at 0; on a full BCD number y(i)₀ will assume the value of the carry (7.6) coming from the right neighbor digit; this carry will not propagate further. This feature allows a parallel digit processing in the BCDx2 procedure.

Steps i and i + 1 of the procedure BCDx_step are defined according to (7.6) to (7.7):

Step i

step i + 1

As quoted above, all the steps may be executed in parallel. The above equations define the procedure BCDx2_step computing the BCD expression of its BCD input multiplied by two:

procedure BCDx2_step (bcd(i): in bcd; 2bcd (i): out bcd)

Algorithm 7.3 describes the binary-to-BCD version of Algorithm 7.1.

Algorithm 7.3 Binary-to-BCD Conversion Algorithm

Example 7.3 Convert in BCD (1011101011101001)₂; n = 16

acc = 1011101011101001

Initial step

Step 1

Step 2

Step 3

Step 4

Step 5

Step 6

Step 7

Step 8

Step 9

Step 10

Step 11

Step 12

Step 13

Step 14

Step 15

(1011101011101001)₂ = (100 0111 1000 0100 1001)_BCD = (47849)₁₀

Comments 7.1 Algorithm 7.3 needs n steps to convert an n-bit binary number into BCD. This figure can go down by processing 2-bit, 3-bit, or 4-bit slices per step, that is, handling the binary vector as a base-4, octal, or hexadecimal number, respectively. Nevertheless, the step complexity will be significantly increased because the adding part is no longer carry-propagation free, as it is in the binary case: adding one unit to an even number (2bcd) never generates a carry.