4.3 INTEGERS

In the case of integer numbers, the addition and subtraction algorithms depend on the particular representation. Three nonredundant representation methods are considered in what follows: B's complement, sign-magnitude, and excess-E (Chapter 3).

4.3.1 B's Complement Addition

Given two n-digit B's complement integers x and y, and an initial carry c_in equal to 0 or 1, then z = x + y + c_in is an (n + 1)-digit B's complement integer. Assume that x and y are represented with n+1 digits. Then the natural numbers associated with x, y, and z are R(x) = x mod Bⁿ⁺¹, R(y) = y mod Bⁿ⁺¹, and R(z) = z mod Bⁿ⁺¹ (Definition 3.4), so that

Thus a straightforward addition algorithm consists in representing x and y with n+1 digits and adding the corresponding natural numbers, as well as the initial carry, modulo Bⁿ⁺¹ (that means without taking into account the output carry). In order to represent x and y with one additional digit, Comment 3.2 is taken into account. As before, the procedure natural_addition computes the sum of two natural numbers.

Algorithm 4.18 B's Complement Addition

if x(n-1)<B/2 then x(n):=0; else x(n):=B-1; end if;
if y(n-1)<B/2 then y(n):=0; else y(n):=B-1; end if;
natural_addition(n+1, c_in, x, y, not_used, z);

Example 4.1 Assume that B = 10, n = 4, c_in = 0, x = −2345, and y = −3674.. Both x and y are negative so that they are represented by R(x) = − 2345 + 10⁴ = 7655 and R(y) = −3674 + 10⁴ = 6326. First represent x and y with five digits: R(x) = 97655 and R(y) = 96326. Then add up R(x) and R(y) modulo 10⁵: (97655 + 96326) mod 10⁵ = 93981. As 9 ≥ B/2 = 5, the integer represented by 93981 is negative and equal to 93981 − 10⁵ = − 6019, that is, the sum of x and y.

4.3.2 B's Complement Sign Change

Given an n-digit B's complement integer x, the inverse z = −x of x is an (n + 1)-digit B's complement integer (actually the only case when − x cannot be represented with n digits is when x = −Bⁿ/2 and − x = Bⁿ/2; i.e., − x = − 0.Bⁿ + (B/2). Bⁿ⁻¹ + 0.Bⁿ⁻² +…+ 0.B⁰). The computation of the representation of −x is based on the following property.

Property 4.3 Given two m-digit base-B natural numbers a = a_m−1B^m−1 + a_m−2. B^m−2 +…+ a₀. B⁰ and b = (B − 1 − a_m−1). B^m−1 + (B − 1 − a_m−2).B^m−2 + … + (B − 1 − a₀).B⁰, then

Assume that x is represented with n + 1 digits, and define x′ as being the natural number deduced from R(x) by substituting every digit x_i by = B − 1 − x_i. Then, according to Property 4.3,

and

A straightforward inversion algorithm consists in representing x with n + 1 digits, complementing every digit to B − 1, then adding 1.

Algorithm 4.19 B's Complement Sign Change

if x(n-1)<B/2 then x(n):=0; else x(n):=B-1; end if;
for i in 0..n loop x′(i):=B-1-y(i); end loop;
natural_addition(n+1, 1, x′, 0, not_used, z);

Examples 4.2

1. Assume that B = 10, n = 4, x = 2345; x is nonnegative and is represented by R(x) = x = 2345. First represent x with five digits: R(x) = 02345. Then complement all digits to B − 1 = 9, and add 1: (97654 + 1) mod 10⁵ = 97655. The integer represented by 97655 is 97655 − 10⁵ = −2345, that is, − x.
2. If x = − 5000 then the four-digit representation of x is 5000 and its five-digit one is 95000. By complementing all digits and adding 1 the obtained result is (04999 + 1) mod 10⁵ = 05000, which is the representation of the nonnegative number 5000.
3. If x = 0 then the four-digit representation of x is 0000 and its five-digit one is 00000. By complementing all digits and adding 1 the obtained result is (99999 + 1) mod 10⁵ = 00000, which is the representation of the nonnegative number 0.

An alternative sign-change algorithm is based on the following observation: if x is represented under the form

where x_k > 0, then the representation of − x is

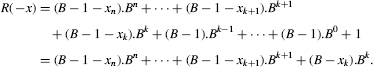
In the following algorithm, the binary variable first_non_zero, initially equal to 0, is set to 1 as soon as the first nonzero digit of x is encountered.

Algorithm 4.20 B's Complement Sign Change (Alternative Algorithm)

if x(n-1)<B/2 then x(n):=0; else x(n):=B-1; end if;
first_non_zero:=0;
for i in 0..n loop
  if first_non_zero=0 then
    if x(i)=0 then z(i):=0; else z(i):=B-x(i); first_non_zero
    :=1; end if;
  else z(i):=B-1-x(i);
  end if;
end loop;

4.3.3 B's Complement Subtraction

Given two n-digit B's complement integers x and y, and an input borrow b_in equal to 0 or 1, then z = x − y − b_in is an (n + 1)-digit B's complement integer. Assume that x and y are represented with n + 1 digits. Then the natural numbers associated with x, − y, and z are R(x) = x mod Bⁿ⁺¹, R(−y) = (y′ + 1) mod Bⁿ⁺¹ (relation (4.15)) and R(z) = z mod Bⁿ⁺¹, so that

Thus a straightforward subtraction algorithm consists in representing x and y with n + 1 digits, complementing the digits of y, and adding, modulo Bⁿ⁺¹, the corresponding natural numbers, as well as the inverted input borrow.

Algorithm 4.21 B's Complement Subtraction

if x(n-1)<B/2 then x(n):=0; else x(n):=B-1; end if;
if y(n-1)<B/2 then y(n):=0; else y(n):=B-1; end if;
for i in 0..n loop y′(i):=B-1-y(i); end loop;
c_in:=1-b_in;
natural_addition(n+1, x, y′, c_in, z, not_used);

Example 4.3 Assume that B = 10, n = 4, b_in = 1, x = − 2345, and y = 3674; x is negative and y nonnegative, so that they are represented by R(x)= − 2345 + 10⁴ = 7655 and R(y) = y = 3674. First represent x and y with five digits: R(x) = 97655 and R(y) = 03674. Then compute y′ = 96325, c_in = 1 − b_in = 0 and (R(x) + y′ + c_in) mod 10⁵ = (97655 + 96325) mod 10⁵ = 93980. The integer represented by 93980 is equal to 93980 − 10⁵ = −6020, that is, −2345−3674− 1.

4.3.4 B's Complement Overflow Detection

In some cases it may be necessary to know whether the result of an operation actually is an (n + 1)-digit number and not an n-digit one. A typical case is the arithmetic unit of a general-purpose computer: both the operands and the result are n-bit numbers, and an overflow flag is raised if the result does not fit within n bits. Assume that the previous algorithms (addition, inversion, and subtraction) are executed without extending the operands to n + 1 bits:

1. Consider the case of addition. An overflow can occur when both operands have the same sign. First observe that if x and y belong to the interval −Bⁿ/2 ≤ x, y < Bⁿ/2, then −Bⁿ ≤ x + y + c_in ≤ 2.(Bⁿ/2 − 1) + 1 = Bⁿ − 1; that is,

   

   So, if x and y are nonnegative, the sum x + y + c_in could be greater than or equal to Bⁿ/2. As R(x) = x and R(y) = y, then R(z) = (x + y + c_in) mod Bⁿ, and according to the previous hypothesis and to (4.16)

   

   that is,

   

   so that z(n) = 0 and z(n − 1) ≥ B/2.

   The conclusion is that the sum of two nonnegative numbers, plus an initial carry, generates an apparently negative number if only n digits are available (z(n − 1) ≥ B/2).

   If x and y are negative the sum x + y + c_in could be smaller than − Bⁿ/2. As R(x) = Bⁿ + x and R(y) = Bⁿ + y, then R(z) = (2.Bⁿ + x + y + c_in) mod Bⁿ, and according to the previous hypothesis and to (4.16)

   

   that is,

   

   so that

   

   The conclusion is that the sum of two negative numbers, plus an initial carry, generates an apparently nonnegative number if only n digits are available (z(n − 1) < B/2).

   To summarize, the overflow detection is carried out just looking at the sign digits of the operands and the result. Under Boolean form:

   

2. It has already been observed that, in the case of the sign-change operation, the only overflow situation is when x = − Bⁿ/2, namely, x(n − 1) = B− 1 and x(n − 2) = … = x(0) = 0. The inversion algorithm, with n digits, generates z = x. Once again it's just a matter of looking at the sign digits of both the operand and the result:

   

3. If a subtraction is performed, an overflow could occur if one operand is negative and the other one nonnegative. First observe that if x and y belong to the interval − Bⁿ/2 ≤ x, y < Bⁿ/2 then − 2.(Bⁿ/2) − 1 < x − y − b_in < 2.(Bⁿ/2), that is,

   

   If x ≥ 0 and y < 0 the difference x − y − b_in could be greater than or equal to Bⁿ/2. As R(x) = x, R(y) = Bⁿ + y, y′ + 1 = Bⁿ − R(y) = −y, R(z) = (R(x) + y′ + 1 − b_in) mod Bⁿ = (x − y − b_in) mod Bⁿ, then according to the previous hypothesis and to (4.19)

   

   so that z(n) = 0, z(n − 1) ≥ B/2.

The conclusion is that the difference between a nonnegative number and a negative one, minus an initial borrow, generates an apparently negative number if only n digits are used (z(n − 1) ≥ B/2).

If x < 0 and y ≥ 0 the difference x − y − b_in could be smaller than − Bⁿ/2. As R(x) = Bⁿ + x, R(y) = y, y′ + 1 = Bⁿ − R(y) = Bⁿ − y, R(z) = (R(x) + y′ + 1 − b_in) mod Bⁿ = (2.Bⁿ + x − y − b_in) mod Bⁿ, then according to the previous hypothesis and to (4.19)

so that z(n) = 1, z(n − 1) < B/2.

The conclusion is that the difference between a negative number and a nonnegative one, minus an initial borrow, generates an apparently nonnegative number if only n digits are used (z(n − 1) ≥ B/2).

As in the preceding cases the overflow detection is carried out just looking at the sign digits of the operands and the result. Under Boolean form:

Examples 4.4 (B = 10, n = 4)

1. Assume that c_in = 0, x = 2345, and y = 4674, and that the value of x + y + c_in is computed. Then R(x) = x = 2345 and R(y) = y = 4674, so that (R(x) + R(x) + c_in) mod 10000 = 7019, that is, the representation of the negative number − 2981.
2. Assume now that c_in = 0, x = − 4726, and y = − 2174, and that the value of x + y + c_in is computed. Then R(x) = 10000 − 4726 = 5274 and R(y) = 10000 − 2174 = 7826, so that (R(x) + R(x) + c_in) mod 10000 = 3100, that is, the representation of the nonnegative number 3100.
3. Compute the difference between x = 2345 and y = − 4726, with b_in = 0. The corresponding representations are R(x) = x = 2345 and R(y) = 10000 − 4726 = 5274, so that y′ = 4725 and (2345 + 4725 + 1) mod 10000 = 7071, that is, the representation of the negative number − 2929.

Comments 4.3 About the reduced B's complement representation (Comment 3.2):

1. The sign extension just consists in duplicating the sign digit.
2. If B = 2, there is no difference between the reduced and the nonreduced 2's complement representation.
3. If x and y are n-digit reduced B's complement numbers, then − Bⁿ⁻¹ ≤ x, y < Bⁿ⁻¹, so that

   

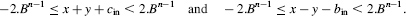
   If, furthermore, B > 2 and B is even, so that B ≥ 4, then 2.Bⁿ⁻¹ ≤ Bⁿ/2 and

   

   Thus both x + y + c_in and x − y − b_in are n-digit B's complement numbers. There is an overflow if the result is not a reduced B's complement number, that is, if the sign digit does not belong to {0, B − 1}. Actually the sign digit is equal to B−2 in the case of a negative overflow (result < − Bⁿ⁻¹) and to 1 in the case of a positive one (result ≥ Bⁿ⁻¹).

Examples 4.5 (B = 10, n = 3, 10's complement reduced form)

1. Assume that c_in = 0, x = 74, and y = 41, and that the value of x + y is computed. Then R(x) = x = 074 and R(y) = y = 041, so that (R(x) + R(x) + c_in) mod 1000 = 115, a number whose sign digit does not belong to {0, 9}.
2. Assume now that c_in = 0, x = − 74, and y = − 41, and that the value of x + y is computed. Then R(x) = 1000 − 74 = 926 and R(y) = 1000 − 41 = 959, so that (R(x) + R(x) + c_in) mod 1000 = 885, a number whose sign digit does not belong to {0, 9}—actually the representation in nonreduced form of 885 − 1000 = −115.
3. Compute the difference between x = 74 and y = − 41, with b_in = 0. The corresponding representations are R(x) = x = 074 and R(y) = 1000 − 41 = 959, so that y′ = 040 and (074 + 040 + 1) mod 1000 = 115, a number whose sign digit does not belong to {0, 9}—actually the representation in nonreduced form of 115.

4.3.5 Excess-E Addition and Subtraction

The addition and subtraction algorithms are based on the following properties.

Properties 4.4 Given two excess-E integers x and y, an initial binary carry c_in and an initial borrow b_in, then

Proof According to Definition 3.3, R(x) = x + E, R(y) = y + E, and R(x + y + c_in) = x + y + c_in + E, so

If x and y are two n-digit excess-E integers, and if z = x + y + c_in is also an n-digit excess-E integer, then a straightforward addition algorithm consists in representing x and y with n + 1 digits, adding them up with c_in and subtracting E. The result R(z) is an (n + 1)-digit natural number whose first digit is 0.

Assume that a procedure natural_subtraction has been defined:

procedure natural_subtraction (s: in natural; borrow: in bit;
x, y: in digit_vector(0..s-1); next_borrow: out bit; z: out
digit_vector(0..s-1);

The following algorithms compute z = x + y + c_in.

Algorithm 4.22 Excess-E Addition

x(n):=0; y(n):=0;
natural_addition(n+1, x, y, c_in, w, not_used);
natural_subtraction(n+1, w, E, 0, z, not_used);
if z(n)>0 then overflow:=true; end if;

Similar algorithms can be defined for computing z = x − y − b_in and z = − x:

Algorithm 4.23 Excess-E Subtraction

x(n):=0; y(n):=0;
natural_addition(n+1, x, E, 0, w, not_used);
natural_subtraction(n+1, w, y, b_in, z, not_used);
if z(n)>0 then overflow:=true; end if;

Algorithm 4.24 Excess-E Sign Change

x(n):=0;
E_by_2(0):=0;
for i in 1..n loop E_by_2(i):=E(i-1); end loop;
natural_subtraction(n+1, E_by_2, x, 0, z, not_used);
if z(n)>0 then overflow:=true; end if;

Examples 4.6 (B = 10, n = 4, excess 5000)

1. Assume that c_in = 0, x = 2345, and y = 1674, and that the value of x+ y+ c_in is computed. Then R(x) = 07345 and R(y) = 06674, so that R(x) + R(y) + c_in − 05000 = 09019, that is, the representation of 4019.
2. Assume now that c_in = 0, x = − 2345, and y = 1674, and that the value of x + y + c_in is computed. Then R(x) = 02655 and R(y) = 06674, so that R(x) + R(y) + c_in − 05000 = 4329, that is, the representation of −671.
3. Compute the sum of x = 2345 and y = 4726, with c_in = 0. The corresponding representations are R(x) = 07345 and R(y) = 09726, so that R(x) + R(y) + c_in − 05000 = 12071 and the overflow flag is raised.
4. Compute the difference between x = 2345 and y = 4726, with b_in = 0. The corresponding representations are R(x) = 07345 and R(y) = 09726, so that R(x) − R(y) − b_in + 05000 = 2619, that is, the representation of −2381.
5. Compute the difference between x = − 2345 and y = 4726, with b_in = 0. The corresponding representations are R(x) = 02655 and R(y) = 09726, so that R(x) − R(y) − b_in + 05000 = 97929 (modulo Bⁿ⁺¹ = 100000) and the overflow flag is raised.
6. Compute the inverse of x = − 5000. The corresponding representation is R(x) = 00000 so that − R(x) + 2 . 05000 = 10000 and the overflow flag is raised.

4.3.6 Sign–Magnitude Addition and Subtraction

Given two n-digit sign-magnitude integers x and y, then z = x + y + c_in is an (n + 1)-digit sign-magnitude integer. The following algorithm computes z.

Algorithm 4.25

if sign(x)=sign(y) then a:=abs(x)+abs(y); else a:=abs(x)-
abs(y);
end if;
if a<0 then sign(z):=sign(y); abs(z):=-a; else sign(z):=
sign(x); abs(z):=a; end if;

It is equivalent to the following algorithm (at the digit level).

Algorithm 4.26 Sign-Magnitude Addition

abs_x:=x(0..n-2)&0; abs_y:=y(0..n-2)&0;
if x(n-1)=y(n-1) then
  natural_addition(n, abs_x, abs_y, 0, a, not_used);
else
  for i in 0..n-1 loop abs_y′(i):=B-1-abs_y(i); end loop;
  natural_addition(n, abs_x, abs_y′, 1, a, not_used);
end if;
if a(n-1)=B-1 then
  z(n):=y(n-1);
  for i in 0..n-1 loop a′(i):=B-1-a(i); end loop;
  natural_addition(n, 0, a′, 1, z(0..n-1), not_used);
else
  z(n):=x(n-1); z(0..n-1):=a;
end if;

Example 4.7 (B = 10, n = 5). Assume that x = +2345 and y = − 7674. First express the absolute values with five digits: abs(x) = 02345 and abs(y) = 07674. As the signs are different, compute 02345 + 92325 + 1 = 94671. The first digit is equal to 9, indicating a negative value. The sign of the result is the same as the sign of y (−) and the absolute value of the result is 05328 + 1 = 05329. So the final result is −5329.

Comment 4.4 With algorithm 4.26, if sign(x) = 0, sign(y) = 1, and abs(x) = abs(y), the result is +0; if sign(x) = 1, sign(y) = 0, and abs(x) = abs(y), the result is − 0.

The subtraction x − y is equivalent to the addition x + minus_y where minus_y = − y, and the computation of minus_y is straightforward:

minus_y(n-1):=1-y(n-1); minus_y (0..n-2):=y(0..n-2);