Chapter 2
Chemical kinetics
Abstract
Chemical reaction types, reaction orders, and the law of mass action that describes the rates of reactions are presented. The Arrhenius rate constant expression and methods for analysis of rate constants, including transition state and recombination rate theories, are discussed as well as the effects of pressure and temperature. Chain reactions are introduced, and steady-state and partial equilibrium approximations are applied for their analysis. The mathematical formalism for large reaction mechanisms is illustrated through the development of the governing equations for coupled thermal and chemical reacting systems without mass diffusion. Finally, sensitivity and rate-of-production analyses are discussed for mechanism analysis as well as methods for mechanism reduction.
Keywords
Arrhenius rate constant; Chemical reactions; Partial equilibrium and steady-state assumptions; Pressure-dependent reactions; Rate-of-production analysis; Reaction rates; Sensitivity analysis; Transition state theory2.1. Introduction
Flames will propagate through only those chemical mixtures that are capable of reacting quickly enough to be considered explosive. Indeed, the expression “explosive” essentially specifies very rapid reaction. From the standpoint of combustion, the interest in chemical kinetic phenomena has generally focused on the conditions under which chemical systems undergo explosive reaction. Recently, however, great interest has developed in the rates and mechanisms of steady (nonexplosive) chemical reactions, since most of the known complex pollutants form in zones of steady, usually lower-temperature, reactions during, and even after, the combustion process. These essential features of chemical kinetics, which occur frequently in combustion phenomena, are reviewed in this chapter. For a more detailed understanding of any of these aspects and a thorough coverage of the subject, refer to any of the books on pure chemical kinetics, such as those listed in Refs [1,2].
2.2. Rates of Reactions and Their Temperature Dependence
All chemical reactions, whether of the hydrolysis, acid–base, or combustion type, take place at a definite rate and depend on the conditions of the system. The most important of these conditions are the concentration of the reactants, the temperature, radiation effects, and the presence of a catalyst or inhibitor. The rate of the reaction may be expressed in terms of the concentration of any of the reacting substances or of any reaction product; that is, the rate may be expressed as the rate of decrease of the concentration of a reactant or the rate of increase of a reaction product.
A stoichiometric relation describing a one-step chemical reaction of arbitrary complexity can be represented by the equation [3,4]
∑nj=1ν′jMj⇄∑nj=1ν″jMj
(2.1)
where ν′j
are the stoichiometric coefficients of the reactants, ν″j
are the stoichiometric coefficients of the products, M is an arbitrary specification of all chemical species, and n is the total number of species involved. If a species represented by Mj does not occur as a reactant or product, its νj equals zero. Consider, as an example, the recombination of H atoms in the presence of H atoms, that is, the reaction
are the stoichiometric coefficients of the reactants, ν″j are the stoichiometric coefficients of the products, M is an arbitrary specification of all chemical species, and n is the total number of species involved. If a species represented by Mj does not occur as a reactant or product, its νj equals zero. Consider, as an example, the recombination of H atoms in the presence of H atoms, that is, the reactionH+H+H→H2+H
n=2,M1=H,M2=H2;
v′1=3,v″1=1,v″2=1
The reason for following this complex notation will become apparent shortly. The law of mass action, which is confirmed experimentally, states that the rate of a chemical reaction, defined as RR, is proportional to the product of the concentrations of the reacting chemical species, where each concentration is raised to a power equal to the corresponding stoichiometric coefficient; that is,
RR∼∏nj=1(Mj)ν′j,RR=k∏nj=1(Mj)ν′j
(2.2)
where k is the proportionality constant called the specific reaction rate coefficient. From Eqn (2.2), the sum of ν′j(∑ν′j)
is also given the symbol n, which is called the overall order of the reaction; ν′j
itself is the order of the reaction with respect to species j. In an actual reacting system, the rate of change of the concentration of a given species i is given by
is also given the symbol n, which is called the overall order of the reaction; ν′j itself is the order of the reaction with respect to species j. In an actual reacting system, the rate of change of the concentration of a given species i is given byd(Mi)dt=[ν″i−ν′i]RR=[ν″i−ν′i]k∏nj=1(Mj)ν′j
(2.3)
since ν″i
moles of Mi are formed for every ν′i
moles of Mi consumed. For the previous example, then, d(H)/dt = −2k(H)3. The use of this complex representation prevents error in sign and eliminates confusion when stoichiometric coefficients are different from 1.
moles of Mi are formed for every ν′i moles of Mi consumed. For the previous example, then, d(H)/dt = −2k(H)3. The use of this complex representation prevents error in sign and eliminates confusion when stoichiometric coefficients are different from 1.In many systems, Mj can be formed not only from a single-step reaction such as that represented by Eqn (2.3), but also from many different such steps, leading to a rather complex formulation of the overall rate as described in Sections 2.3 and 2.8. However, for a single-step reaction such as Eqn (2.3), ∑ν′j
represents not only the overall order of the reaction but also the molecularity, which is defined as the number of molecules that interact in the reaction step. Generally the molecularity of most reactions of interest will be 2 or 3. For a complex reaction scheme, the concept of molecularity is not appropriate, and the overall order can take various values including fractional ones.
represents not only the overall order of the reaction but also the molecularity, which is defined as the number of molecules that interact in the reaction step. Generally the molecularity of most reactions of interest will be 2 or 3. For a complex reaction scheme, the concept of molecularity is not appropriate, and the overall order can take various values including fractional ones.The convention used throughout this book is that parentheses around a chemical symbol signify the concentration of that species in moles or mass per cubic centimeter. Also note that the molar concentration of a species Mj can be related to the mole fraction of that species through the ideal gas equation of state XjP = (Mj
)RT.
)RT.2.2.1. The Arrhenius Rate Expression
In most chemical reactions, the rates are dominated by collisions of two species that may have the capability to react. Thus, most simple reactions are second-order. Other reactions are dominated by a loose bond-breaking step and thus are first-order. Most of these latter type reactions fall in the class of decomposition processes. Isomerization reactions are also found to be first-order. According to Lindemann's theory [1,5] of first-order processes, first-order reactions occur as a result of a two-step process. This point will be discussed in a subsequent section.
An arbitrary second-order reaction may be written as
A+B→C+D
(2.4)
where a real example would be the reaction of oxygen atoms with nitrogen molecules:
O+N2→NO+N
For the arbitrary reaction (2.4), the rate expression takes the form
−RR=d(A)dt=−k(A)(B)=d(B)dt=−d(C)dt=−d(D)dt
(2.5)
Here, the term (ν″j−ν′j),
which is present in Eqn (2.3), is −1 for the rate expressions of species A and B and 1 for the rate expressions of species C and D. Specifying the reaction in this manner does not infer that every collision of the reactants A and B would lead to products or cause the disappearance of either reactant. Arrhenius [6] put forth a simple theory that accounts for this fact and gives a temperature dependence of k. According to Arrhenius, only molecules that possess energy greater than a certain amount, E, will react. Molecules acquire the additional energy necessary from collisions induced by the thermal condition that exists. These high-energy activated molecules lead to products. Arrhenius' postulate may be written as
which is present in Eqn (2.3), is −1 for the rate expressions of species A and B and 1 for the rate expressions of species C and D. Specifying the reaction in this manner does not infer that every collision of the reactants A and B would lead to products or cause the disappearance of either reactant. Arrhenius [6] put forth a simple theory that accounts for this fact and gives a temperature dependence of k. According to Arrhenius, only molecules that possess energy greater than a certain amount, E, will react. Molecules acquire the additional energy necessary from collisions induced by the thermal condition that exists. These high-energy activated molecules lead to products. Arrhenius' postulate may be written asRR=ZABexp(−E/RT)
(2.6)
where ZAB is the gas kinetic collision frequency and exp(−E/RT) is the Boltzmann factor. Kinetic theory shows that the Boltzmann factor gives the fraction of all collisions that have a translational kinetic energy along the internuclear axis greater than E.
Thus, the energy term in the Boltzmann factor may be considered as the size of the barrier along a potential energy surface for a system of reactants going to products, as shown schematically in Figure 2.1. The state of the reacting species at this activated energy can be regarded as some intermediate complex that leads to the products. This energy is referred to as the activation energy of the reaction and is generally given the symbol EA. In Figure 2.1, this energy is given the symbol Ef, to distinguish it from the condition in which the product species can revert to reactants by a backward reaction. The activation energy of this backward reaction is represented by Eb and is obviously much larger than Ef for the forward step.
Figure 2.1 shows an exothermic condition for reactants going to products. The relationship between the activation energy and the heat of reaction has been developed [2]. Generally, the more exothermic a reaction is, the smaller the activation energy. In complex systems, the energy release from one such reaction can sustain other, endothermic reactions, such as that represented in Figure. 2.1 for products reverting back to reactants. For example, once the reaction is initiated, acetylene will decompose to the elements in a monopropellant rocket in a sustained fashion because the energy release of the decomposition process is greater than the activation energy of the process. In contrast, a calculation of the decomposition of benzene shows the process to be exothermic, but the activation energy of the benzene decomposition process is so large that it will not sustain monopropellant decomposition. For this reason, acetylene is considered an unstable species and benzene a stable one.
Considering again Eqn (2.6) and referring to E as an activation energy, attention is focused on the collision rate ZAB, which from simple kinetic theory can be represented by
ZAB=(A)(B)σ2AB[8πkBT/μ]1/2
(2.7)
where σAB is the hard sphere collision diameter, kB is the Boltzmann constant, μ is the reduced mass [mAmB/(mA + mB)], and m is the mass of the species. ZAB may be written in the form
ZAB=Z′AB(A)(B)
(2.8)
where Z′AB=σ2AB[8πkBT/μ]1/2
. Thus, the Arrhenius form for the rate is
. Thus, the Arrhenius form for the rate isRR=Z′AB(A)(B)exp(−E/RT)
When one compares this with the reaction rate written from the law of mass action (Eqn (2.2)), one finds that
k=Z′ABexp(−E/RT)=Z″ABT1/2exp(−E/RT)
(2.9)
where Z″AB
is a constant, which is independent of the local thermodynamic state. Thus, the important conclusion is that the specific reaction rate constant k is dependent on temperature alone and is simply independent of concentration. Actually, when complex molecules are reacting, not every collision has the proper steric orientation for the specific reaction to take place. To include the steric probability, one writes k as
is a constant, which is independent of the local thermodynamic state. Thus, the important conclusion is that the specific reaction rate constant k is dependent on temperature alone and is simply independent of concentration. Actually, when complex molecules are reacting, not every collision has the proper steric orientation for the specific reaction to take place. To include the steric probability, one writes k ask=Z″ABT1/2[exp(−E/RT)]℘
(2.10)
where ℘ is a steric factor, which can be a very small number at times. Most generally, however, the Arrhenius form of the reaction rate constant is written as
k=constT1/2exp(−E/RT)=Aexp(−E/RT)
(2.11)
where the constant A takes into account the steric factor and the terms in the collision frequency other than the concentrations and is referred to as the kinetic pre-exponential A factor. The factor A as represented in Eqn (2.11) has a very mild T1/2 temperature dependence that is generally ignored when plotting data. The form of Eqn (2.11) holds well for many reactions, showing an increase in k with T that permits convenient straight-line correlations of data on ln k versus (1/T) plots. Data that correlate as a straight line on a ln k versus (1/T) plot are said to follow Arrhenius kinetics, and plots of the logarithm of rates or rate constants as a function of (1/T) are referred to as Arrhenius plots. The slopes of lines on these plots are equal to (−E/R); thus, the activation energy may be determined readily (see Figure 2.2). Low activation energy processes generally proceed faster than high activation energy processes at low temperatures and are much less temperature-sensitive. At high temperatures, high activation energy reactions can prevail because of this temperature sensitivity.
2.2.2. Transition State and Recombination Rate Theories
There are two classes of reactions for which Eqn (2.11) is not suitable. Recombination reactions and low activation energy free-radical reactions in which the temperature dependence in the pre-exponential term assumes more importance. In this low-activation, free-radical case the approach known as absolute or transition state theory of reaction rates develops a more appropriate correlation of reaction rate data with temperature. In this theory the reactants are assumed to be in equilibrium with an activated complex. One of the vibrational modes in the complex is considered loose and permits the complex to dissociate to products. Figure 2.1 is again an appropriate representation, where the reactants are in equilibrium with an activated complex, which is shown by the curve peak along the extent of the reaction coordinate. When the equilibrium constant for this situation is written in terms of partition functions and if the frequency of the loose vibration is allowed to approach zero, a rate constant can be derived in the following fashion.
The concentration of the activated complex may be calculated by statistical thermodynamics in terms of the reactant concentrations and an equilibrium constant [1,7]. If the reaction scheme is written as
A+BC⇄(ABC)#→AB+C
(2.12)
the equilibrium constant with respect to the reactants may be written as
K#=(ABC)#(A)(BC)
(2.13)
where the symbol # refers to the activated complex. As discussed in Chapter 1, since K# is expressed in terms of concentration, it is pressure-dependent. Statistical thermodynamics relates equilibrium constants to partition functions; thus, for the case in question, one finds [7]
K#=(QT)#(QT)A(QT)BCexp(−ERT)
(2.14)
where QT is the total partition function of each species in the reaction. QT can be considered separable into vibrational, rotational, and translation partition functions.
However, one of the terms in the vibrational partition function part of Q# is different in character from the rest because it corresponds to a very loose vibration that allows the complex to dissociate into products. The complete vibrational partition function for harmonic oscillators is written as
Qvib=∏i[1−exp(−hνi/kBT)]−1
(2.15)
where h is Planck's constant and νi is the vibrational frequency of the ith mode. For the loose vibration, one term of the complete vibrational partition function can be separated and its value employed when ν tends to zero,
limν→0[1−exp(−hν/kBT)]−1=(kBT/hν)
(2.16)
Thus,
{(ABC)#/[(A)(BC)]}={[(QT−1)#(kBT/hν)]/[(QT)A(QT)BC]}×exp(−E/RT)
(2.17)
which rearranges to
ν(ABC)#={[(A)(BC)(kBT/h)(QT−1)#]/[(QT)A(QT)BC]}×exp(−E/RT)
(2.18)
where (QT−1)# is the partition function of the activated complex evaluated for all vibrational frequencies except the loose one. The term v(ABC)# on the left-hand side of Eqn (2.18) is the frequency of the activated complex in the degree of freedom corresponding to its decomposition mode and is therefore the frequency of decomposition. Thus,
k=(kBT/h)[(QT−1)#/(QT)A(QT)BC]exp(−E/RT)
(2.19)
is the expression for the specific reaction rate as derived from transition state theory.
If species A is only a diatomic molecule, the reaction scheme can be represented by
A⇄A#→products
(2.20)
Thus, (QT−1)# goes to 1. There is only one bond in A, so
Qvib,A=[1−exp(−hνA/kBT)]−1
(2.21)
Then
k=(kBT/h)[1−exp(−hνA/kBT)]exp(−E/RT)
(2.22)
If νA of the stable molecule is large, which normally it is in decomposition systems, then the term in square brackets simply goes to 1 and
k=(kBT/h)exp(−E/RT)
(2.23)
Note that the term (kBT/h) gives a general order of the pre-exponential term for these dissociation processes.
Although the rate constant will increase monotonically with T for Arrhenius' collision theory, examination of Eqns (2.19) and (2.23) reveals that a nonmonotonic trend can be found [8] for the low activation energy processes represented by transition state theory. Thus, data that show curvature on an Arrhenius plot probably represent a reacting system in which an intermediate complex forms and in which the activation energy is low. As the results from Problem 1 of this chapter reveal, the term (kBT/h) and the Arrhenius pre-exponential term given by Eqn (2.8) are approximately the same and/or are about 1014 cm3 mol−1 s−1 at 1000 K. This agreement is true when there is little entropy change between the reactants and the transition state and is nearly true for most cases. Thus, one should generally expect pre-exponential values to fall in a range near 1013–1014 cm3 mol−1 s−1. When quantities far different from this range are reported, one should conclude that the representative expression is an empirical fit to some experimental data over a limited temperature range. The earliest representation of an important combustion reaction that showed curvature on an Arrhenius plot was for the CO + OH reaction as given in Ref. [8], which, by application of transition state theory, correlated a wide temperature range of experimental data. Since then, consideration of transition state theory has been given to many other reactions important to combustion [9].
The use of transition state theory as a convenient expression of rate data is obviously complex owing to the presence of the temperature-dependent partition functions. Most researchers working in the area of chemical kinetic modeling have found it necessary to adopt a uniform means of expressing the temperature variation of rate data and consequently have adopted a modified Arrhenius form:
k=ATnexp(−E/RT)
(2.24)
where the power of T accounts for all the pre-exponential temperature-dependent terms in Eqns (2.11), (2.19), and (2.23). Since most elementary binary reactions exhibit Arrhenius behavior over modest ranges of temperature, the temperature dependence can usually be incorporated with sufficient accuracy into the exponential alone; thus, for most data n = 0 is adequate, as will be noted for the extensive listing in the appendixes. However, for the large temperature ranges found in combustion, “non-Arrhenius” behavior of rate constants tends to be the rule rather than the exception, particularly for processes that have a small energy barrier. It should be noted that for these processes the pre-exponential factor that contains the ratio of partition functions (which are weak functions of temperature compared to an exponential) corresponds roughly to a Tn dependence with n in the ±1–2 range [10]. Indeed the values of n for the rate data expressions reported in the appendixes fall within this range. Generally, the values of n listed apply only over a limited range of temperatures, and they may be evaluated by the techniques of thermochemical kinetics [11].
The units for the reaction rate constant k when the reaction is of order n (different from the n power of T) will be [(conc)n−1 (time)]−1. Thus, for a first-order reaction the units of k are in reciprocal seconds (s−1), and for a second-order reaction process the units are in cubic centimeter per mole per second (cm3 mol−1 s−1). Thus, as shown in Appendix C, the most commonly used units for kinetic rates are cubic centimeter, mole, and kilojoules, where kilojoules are used for the activation energy.
Radical recombination is another class of reactions in which the Arrhenius expression will not hold. When simple radicals recombine to form a product, the energy liberated in the process is sufficiently great to cause the product to decompose into the original radicals. Ordinarily, a third body is necessary to remove this energy to complete the recombination. If the molecule formed in a recombination process has a large number of internal (generally vibrational) degrees of freedom, it can redistribute the energy of formation among these degrees, so a third body is not necessary. In some cases the recombination process can be stabilized if the formed molecule dissipates some energy radiatively (chemiluminescence) or collides with a surface and dissipates energy in this manner.
If one follows the early approach of Landau and Teller [12], who in dealing with vibrational relaxation developed an expression by averaging a transition probability based on the relative molecular velocity over the Maxwellian distribution, one can obtain the following expression for the recombination rate constant [7]:
k∼exp(C/T)1/3
(2.25)
where C is a positive constant that depends on the physical properties of the species of concern [7]. Thus, for radical recombination, the reaction rate constant decreases mildly with the temperature, as one would intuitively expect. In dealing with the recombination of radicals in nozzle flow, one should keep this mild temperature dependence in mind. Recall the example of H atom recombination given earlier. If one writes M as any (or all) third body in the system, the equation takes the form
H+H+M→H2+M
(2.26)
The rate of formation of H2 is third-order and given by
d(H2)/dt=k(H)2(M)
(2.27)
Thus, in expanding dissociated gases through a nozzle, the velocity increases and the temperature and pressure decrease. The rate constant for this process thus increases, but only slightly. The pressure affects the concentrations, and since the reaction is third-order, it enters the rate as a cubed term. In all, then, the rate of recombination in the high-velocity expanding region decreases owing to the pressure term. The point to be made is that third-body recombination reactions are mostly pressure-sensitive, generally favored at higher pressure, and rarely occur at very low pressures.
2.3. Simultaneous Interdependent Reactions
In complex reacting systems, such as those in combustion processes, a simple one-step rate expression will not suffice. Generally, one finds simultaneous, interdependent reactions or chain reactions.
The most frequently occurring simultaneous, interdependent reaction mechanism is the case in which the product, as its concentration is increased, begins to dissociate into the reactants. The classical example is the hydrogen iodine reaction:
H2+I2kf⇄kb2HI
(2.28)
The rate of formation of HI is then affected by two rate constants, kf and kb, and is written as
d(HI)/dt=2kf(H2)(I2)−2kb(HI)2
(2.29)
in which the numerical value 2 should be noted. At equilibrium, the rate of formation of HI is zero, and one finds that
2kf(H2)eq(I2)eq−2kb(HI)2eq=0
(2.30)
where the subscript eq designates the equilibrium concentrations. Thus,
kfkb=(HI)2eq(H2)eq(I2)eq≡Kc
(2.31)
that is, the forward and backward rate constants are related to the equilibrium constant K based on concentrations (Kc). The equilibrium constants are calculated from basic thermodynamic principles as discussed in Chapter 1 Section 1.3, and the relationship (kf/kb) = Kc holds for any reacting system. The calculation of the equilibrium constant is much more accurate than experimental measurements of specific reaction rate constants. Thus, given a measurement of a specific reaction rate constant, the reverse rate constant is determined from the relationship Kc ≡ (kf/kb). For the particular reaction in Eqn (2.31). Kc is not pressure-dependent, as there is a concentration squared in both the numerator and denominator. Indeed, Kc = (kf/kb) = Kp only when the concentration powers cancel.
With consideration of this equilibrium condition, the rate expression for the formation of HI becomes
d(HI)dt=2kf(H2)(I2)−2kfKc(HI)2
(2.32)
2.4. Chain Reactions
In most instances, two reacting molecules do not react directly as H2 and I2 do; rather one molecule dissociates first to form radicals. These radicals then initiate a chain of steps. Interestingly, this procedure occurs in the reaction of H2 with another halogen, bromine (Br2). Experimentally, Bodenstein [13] found that the rate of formation of HBr obeys the expression
d(HBr)dt=k′exp(H2)(Br2)1/21+k″exp[(HBr)/(Br2)]
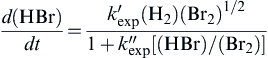(2.33)
This expression shows that HBr is inhibiting to its own formation.
Bodenstein explained this result by suggesting that the H2–Br2 reaction was chain in character and initiated by a radical (Br·) formed by the thermal dissociation of Br2. He proposed the following steps:
(i)M+Br2ki→2Br·+M}chaininitiatingstep(ii)Br·+H2kii→HBr+H·(iii)H·+Br2kiii→HBr+Br·(iv)H·+HBrkiv→H2+Br·}chaincarryingorpropagatingsteps(v)M+2Br·kv→Br2+M}chainterminatingstep
The Br2 bond energy is approximately 189 kJ/mol, and the H2 bond energy is approximately 427 kJ/mol. Consequently, except for very high temperatures, Br2 dissociation will be the initiating step. These dissociation steps follow Arrhenius kinetics and form a plot similar to that shown in Figure. 2.2. In Figure 2.3 two Arrhenius plots are shown, one for a high activation energy step and another for a low activation energy step. One can readily observe that for low temperature, the smaller EA step prevails.
Perhaps the most important of the various chain types is the chain step that is necessary to achieve nonthermal explosions. This chain step, called chain branching, is one in which two radicals are created for each radical consumed. Two typical chain branching steps that occur in the H2–O2 reaction system are
H·+O2→·OH+·O·
·O·+H2→·OH+H·
where the dot next to or over a species is the convention for designating a radical. Such branching will usually occur when the monoradical (such as H·) formed by breaking a single bond reacts with a species containing a double bond type structure (such as that in O2) or when a biradical (·O·) formed by breaking a double bond reacts with a saturated molecule (such as H2 or RH, where R is any organic radical). For an extensive discussion of chain reactions, refer to the monograph by Dainton [14].
As shown in the H2–Br2 example, radicals are produced by dissociation of a reactant in the initiation process. These types of dissociation reactions are highly endothermic and therefore quite slow. The activation energy of these processes would be in the range of 160–460 kJ/mol. Propagation reactions similar to reactions (ii)–(iv) in the H2–Br2 example are important because they determine the rate at which the chain continues. For most propagation reactions of importance in combustion, activation energies normally lie between 0 and 40 kJ/mol. Obviously, branching chain steps are a special case of propagating steps and, as mentioned, these are the steps that lead to explosion. Branching steps need not necessarily occur rapidly because of the multiplication effect; thus, their activation energies may be higher than those of the linear propagation reactions with which they compete [15].
Termination occurs when two radicals recombine; they need not be similar to those shown in the H2–Br2 case. Termination can also occur when a radical reacts with a molecule to give either a molecular species or a radical of lower activity that cannot propagate a chain. Since recombination processes are exothermic, the energy developed must be removed by another source, as discussed previously. The source can be another gaseous molecule M, as shown in the example, or a wall. For the gaseous case, a termolecular or third-order reaction is required; consequently, these reactions are slower than other types except at high pressures.
In writing chain mechanisms note that backward reactions are often written as an individual step; that is, reaction (iv) of the H2–Br2 scheme is the backward step of reaction (ii). The inverse of reaction (iii) proceeds very slowly; it is therefore not important in the system and is usually omitted for the H2–Br2 example.
From the five chain steps written for the H2–Br2 reaction, one can write an expression for the HBr formation rate:
d(HBr)dt=kii(Br)(H2)+kiii(H)(Br2)−kiv(H)(HBr)
(2.34)
In experimental systems, it is usually very difficult to measure the concentration of the radicals that are important intermediates. However, one would like to be able to relate the radical concentrations to other known or measurable quantities. It is possible to achieve this objective by the so-called steady-state approximation for the reaction's radical intermediates. The assumption is that the radicals form and react very rapidly, thereby approximating a steady-state concentration. Thus, one writes the equations for the rate of change of the radical concentration, then sets them equal to zero. For the H2–Br2 system, then, one has for (H) and (Br)
d(H)dt=kii(Br)(H2)−kiii(H)(Br2)−kiv(H)(HBr)≅0
(2.35)
d(Br)dt=2ki(Br2)(M)−kii(Br)(H2)+kiii(H)(Br2)+kiv(H)(HBr)−2kv(Br)2(M)≅0
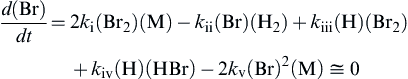(2.36)
Writing these two equations equal to zero does not imply that equilibrium conditions exist, as was the case for Eqn (2.30). It is also important to realize that the steady-state approximation does not imply that the rate of change of the radical concentration is necessarily zero, but rather that the rate terms for the expressions of radical formation and disappearance are much greater than the radical concentration rate term. That is, the sum of the positive terms and the sum of the negative terms on the right-hand side of the equality in Eqns (2.35) and (2.36) are, in absolute magnitude, very much greater than the term on the left of these equalities [4].
Thus in the H2–Br2 experiment it is assumed that steady-state concentrations of radicals are approached, and the concentrations for H and Br are found to be
(Br)=(ki/kv)1/2(Br2)1/2
(2.37)
(H)=kii(ki/kv)1/2(H2)(Br2)1/2kiii(Br2)+kiv(HBr)
(2.38)
By substituting these values in the rate expression for the formation of HBr (Eqn (2.34)), one obtains
d(HBr)dt=2kii(ki/kv)1/2(H2)(Br2)1/21+[kiv(HBr)/kiii(Br2)]
(2.39)
which is the exact form found experimentally (Eqn (2.33)). Thus,
k′exp=2kii(ki/kv)1/2,k″exp=kiv/kiii
Consequently, it is seen, from the measurement of the overall reaction rate and the steady-state approximation, that the values of the rate constants of the intermediate radical reactions can be determined without any measurement of radical concentrations. Values k′exp
and k″exp
evolve from the experimental measurements and the form of Eqn (2.33). Since (ki/kv) is the inverse of the equilibrium constant for Br2 dissociation and this value is known from thermodynamics, kii can be found from k′exp.
The value of kiv is found from kii and the equilibrium constant that represents reactions (ii) and (iv), as written in the H2–Br2 reaction scheme. From the experimental value of k″exp and the calculated value of kiv, the value kiii can be determined.
and k″exp evolve from the experimental measurements and the form of Eqn (2.33). Since (ki/kv) is the inverse of the equilibrium constant for Br2 dissociation and this value is known from thermodynamics, kii can be found from k′exp. The value of kiv is found from kii and the equilibrium constant that represents reactions (ii) and (iv), as written in the H2–Br2 reaction scheme. From the experimental value of k″exp and the calculated value of kiv, the value kiii can be determined.The steady-state approximation, found to be successful in application to this straight-chain process, can be applied to many other straight-chain processes, chain reactions with low degrees of branching, and other types of nonchain systems. Because the rates of the propagating steps greatly exceed those of the initiation and termination steps in most, if not practically all, of the straight-chain systems, the approximation always works well. However, the use of the approximation in the initiation or termination phase of a chain system, during which the radical concentrations are rapidly increasing or decreasing, can lead to substantial errors.
2.5. Pseudo-First-Order Reactions and the “Falloff” Range
As presented earlier, practically all reactions are initiated by bimolecular collisions; however, certain bimolecular reactions exhibit first-order kinetics. Whether a reaction is first- or second-order is particularly important in combustion because of the presence of large radicals that decompose into a stable species and a smaller radical (primarily the hydrogen atom). A prominent combustion example is the decay of a paraffinic radical to an olefin and an H atom. The order of such reactions, and hence the appropriate rate constant expression, can change with the pressure. Thus, the rate expression developed from one pressure and temperature range may not be applicable to another range. This question of order was first addressed by Lindemann [5], who proposed that first-order processes occur as a result of a two-step reaction sequence in which the reacting molecule is activated by collisional processes, after which the activated species decomposes to products. Similarly, the activated molecule could be deactivated by another collision before it decomposes. If A is considered the reactant molecule and M its nonreacting collision partner, the Lindemann scheme can be represented as follows:
A+Mkf⇄kbA∗+M
(2.40)
A∗kp→products
(2.41)
The rate of decay of species A is given by
d(A)dt=−kf(A)(M)+kb(A∗)(M)
(2.42)
and the rate of change of the activated species A∗ is given by
d(A∗)dt=kf(A)(M)−kb(A∗)(M)−kp(A∗)≅0
(2.43)
Applying the steady-state assumption to the activated species equation gives
(A∗)=kf(A)(M)kb(M)+kp
(2.44)
Substituting this value of (A∗) into Eqn (2.42), one obtains
−1(A)d(A)dt=kfkp(M)kb(M)+kp=kdiss
(2.45)
where kdiss is a function of the rate constants and the collision partner concentration—that is, a direct function of the total pressure if the effectiveness of all collision partners is considered the same. Owing to size, complexity, and the possibility of resonance energy exchange, the effectiveness of a collision partner (third body) can vary. Normally, collision effectiveness is not a concern, but for some reactions specific molecules may play an important role [16].
At high pressures, kb(M) >> kp and
kdiss,∞≡kfkpkb=Kkp
(2.46)
where kdiss,∞ becomes the high-pressure limit rate constant and K is the equilibrium constant (kf/kb). Thus at high pressures the decomposition process becomes overall first-order. At low pressure, kb(M) << kp as the concentrations drop and
kdiss,0≡kf(M)
(2.47)
where kdiss,0 is the low-pressure limit rate constant. The process is then second-order by Eqn (2.45), simplifying to −d(A)/dt = kf(M)(A). Note the presence of the concentration (A) in the manner in which Eqn (2.45) is written.
Many systems fall in a region of pressures (and temperatures) between the high- and low-pressure limits. This region is called the “falloff range,” and its importance to combustion problems has been very adequately discussed by Troe [17]. The question, then, is how to treat rate processes in the falloff range. Troe proposed that the falloff range between the two limiting rate constants be represented using a dimensionless pressure scale
(kdiss,0/kdiss,∞)=kb(M)/kp
(2.48)
in which one must realize that the units of kb and kp are different so that the right-hand side of Eqn (2.48) is dimensionless. Substituting Eqn (2.46) into Eqn (2.45), one obtains
kdisskdiss,∞=kb(M)kb(M)+kp=kb(M)/kp[kb(M)/kp]+1
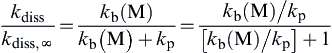(2.49)
or, from Eqn (2.48)
kdisskdiss,∞=kdiss,0/kdiss,∞1+(kdiss,0/kdiss,∞)
(2.50)
For a pressure (or concentration) in the center of the falloff range, (kdiss,0/kdiss,∞) = 1 and
kdiss=0.5kdiss,∞
(2.51)
Since it is possible to write the products designated in Eqn (2.41) as two species that could recombine, it is apparent that recombination reactions can exhibit pressure sensitivity; so an expression for the recombination rate constant similar to Eqn (2.50) can be developed [17].
The preceding discussion stresses the importance of properly handling rate expressions for thermal decomposition of polyatomic molecules, a condition that prevails in many hydrocarbon oxidation processes. For a detailed discussion on evaluation of low- and high-pressure rate constants, again refer to Ref. [17].
Another example in which a pseudo-first-order condition can arise in evaluating experimental data is the case in which one of the reactants (generally the oxidizer in a combustion system) is in large excess. Consider the arbitrary process
A+B→D
(2.52)
where (B) >> (A). The rate expression is
d(A)dt=−d(D)dt=−k(A)(B)
(2.53)
Since (B) >> (A), the concentration of B does not change appreciably and k(B) would appear as a constant. Then Eqn (2.53) becomes
d(A)dt=−d(D)dt=−k′(A)
(2.54)
where k′ = k(B). Equation (2.54) could represent experimental data because there is little dependence on variations in the concentration of the excess component B. The reaction, of course, appears overall first-order. One should keep in mind, however, that k′ contains a concentration and is pressure-dependent. This pseudo-first-order concept arises in many practical combustion systems that are very fuel-lean; that is, O2 is present in large excess.
2.6. The Partial Equilibrium Assumption
As will be discussed in the following chapter, most combustion systems entail oxidation mechanisms with numerous individual reaction steps. Under certain circumstances a group of reactions will proceed rapidly and reach a quasi-equilibrium state. Concurrently, one or more reactions may proceed slowly. If the rate or rate constant of this slow reaction is to be determined and if the reaction contains a species difficult to measure, it is possible through a partial equilibrium assumption to express the unknown concentrations in terms of other measurable quantities. Thus, the partial equilibrium assumption is very much like the steady-state approximation discussed earlier. The difference is that in the steady-state approximation one is concerned with a particular species and in the partial equilibrium assumption one is concerned with particular reactions. Essentially then, partial equilibrium comes about when forward and backward rates are very large, and the contribution that a particular species makes to a given slow reaction of concern can be compensated for by very small differences in the forward and backward rates of those reactions in partial equilibrium.
A specific example can illustrate the use of the partial equilibrium assumption. Consider, for instance, a complex reacting hydrocarbon in an oxidizing medium. By the measurement of the CO and CO2 concentrations, one wants to obtain an estimate of the rate constant of the reaction
CO+OH→CO2+H
(2.55)
The rate expression is
d(CO2)dt=−d(CO)dt=k(CO)(OH)
(2.56)
Then the question is how to estimate the rate constant k without a measurement of the OH concentration. If one assumes that equilibrium exists between the H2–O2 chain species, one can develop the following equilibrium reactions of formation from the complete reaction scheme:
12H2+12O2⇄OH,H2+12O2⇄H2O
K2C,f,OH=(OH)2eq(H2)eq(O2)eq,KC,f,H2O=(H2O)eq(H2)eq(O2)1/2eq
(2.57)
Solving the two latter expressions for (OH)eq and eliminating (H2)eq, one obtains
(OH)eq=(H2O)1/2(O2)1/4[K2C,f,OH/KC,f,H2O]1/2
(2.58)
d(CO2)dt=−d(CO)dt=k[K2C,f,OH/KC,f,H2O]1/2(CO)(H2O)1/2(O2)1/4
(2.59)
Thus, one observes that the rate expression can be written in terms of readily measurable stable species. One must, however, exercise care in applying this assumption. Equilibria do not always exist among the H2–O2 reactions in a hydrocarbon combustion system—indeed, there is a question if equilibrium exists during CO oxidation in a hydrocarbon system. Nevertheless, it is interesting to note the availability of experimental evidence that shows the rate of formation of CO2 to be one-fourth-order with respect to O2, one-half-order with respect to water, and first-order with respect to CO [18,19]. The partial equilibrium assumption is more appropriately applied to NO formation in flames, as will be explained in Chapter 8.
2.7. Pressure Effect in Fractional Conversion
In combustion problems, one is interested in the rate of energy conversion or utilization. Thus, it is more convenient to deal with the fractional change of a particular substance rather than the absolute concentration. If (A) is used to denote the concentrations in a chemical reacting system A → B of arbitrary order n, the rate expression is
d(A)dt=−k(A)n
(2.60)
Since (A) is a concentration, it may be written in terms of the total concentration of the system (M) (i.e., P = (M)RT) and the mole fraction XA, which in this instance is the number of moles of species A relative to the total number of moles of the system; that is,
XA=(A)/(M)
(2.61)
It follows that at constant pressure and temperature
(M)dXAdt=−k((M)XA)n
(2.62)
dXAdt=−kXnA(M)n−1
(2.63)
For a constant-temperature system, (M) ∼ P and
(dXA/dt)∼Pn−1
(2.64)
That is, the fractional change is proportional to the pressure raised to the reaction order minus one.
2.8. Chemical Kinetics of Large Reaction Mechanisms
For systems with large numbers of species and reactions, the dynamics of the reaction and the interactions between species can become quite complex. In order to analyze the reaction progress of species, various diagnostic techniques have been developed. Two of these techniques are reaction rate-of-production analysis and sensitivity analysis. A sensitivity analysis identifies the rate-limiting or rate-controlling reaction steps, while a rate-of-production analysis identifies the dominant reaction paths (i.e., those most responsible for forming or consuming a particular species).
First, as mentioned previously, for a system of reactions, Eqn (2.1) can be rewritten as
∑nj=1ν′jiMj⇄∑nj=1ν″jiMji,=1,…,m
(2.65)
where the index i refers to reactions 1 through m of the mechanism. Following Eqn (2.3), the net reaction rate for the ith reaction can then be expressed as
qi=kf,i∏nj=1(Mj)ν′ji−kb,i∏nj=1(Mj)ν″ji
(2.66)
From Eqn (2.3), the rate of change of concentration of a given species j resulting from both the forward and backward reactions of the ith reaction is given by
˙ωji=[ν″ji−ν′ji]qi=νjiqi
(2.67)
Given m reactions in the mechanism, the rate of change of concentration of the jth species resulting from all m reactions is given by
˙ωj=∑mi=1νjiqi
(2.68)
For a temporally reacting system at constant temperature, the coupled species equations are then
d(Mj)dt=˙ωjj=1,…,n
(2.69)
These equations are a set of nonlinear first-order ordinary differential equations that describe the evolution of the n species as a function of time starting from a set of initial conditions:
(Mj)t=0=(Mj)0j=1,…,n
(2.70)
Because the rates of reactions can be vastly different, the timescales of change of different species concentrations can vary significantly. As a consequence, the equations are said to be stiff and require specialized numerical integration routines for their solution [20]. Solution methods that decouple the timescales of the different species (e.g., to eliminate the fast processes if only the slow rate-limiting processes are of concern) have also been developed [21,22].
2.8.1. Sensitivity Analysis
The sensitivity analysis of a system of chemical reactions consists of the problem of determining the effect of uncertainties in parameters and initial conditions on the solution of a set of ordinary differential [23,24]. Sensitivity analysis procedures may be classified as deterministic or stochastic in nature. The interpretation of system sensitivities in terms of first-order elementary sensitivity coefficients is called a local sensitivity analysis and typifies the deterministic approach to sensitivity analysis. Here, the first-order elementary sensitivity coefficient is defined as the gradient,
∂(Mj)/∂αi
where (Mj) is the concentration of the jth species at time t and αi is the ith input parameter (e.g., rate constant), and the gradient is evaluated at a set of nominal parameter values ˉα
. Although the linear sensitivity coefficients ∂(Mj)/∂αi provide direct information on the effect of a small perturbation in each parameter about its nominal value on each concentration j, they do not necessarily indicate the effect of simultaneous, large variations in all parameters on each species concentration. An analysis that accounts for simultaneous parameter variations of arbitrary magnitude can be termed a global sensitivity analysis. This type of analysis produces coefficients that have a measure of sensitivity over the entire admissible range of parameter variation. Examples include the “brute force” method, where a single parameter value is changed and the time history of species profiles with and without the modification is compared. Other methods are the FAST method [25], Monte Carlo method [26], and Pattern method [27].
. Although the linear sensitivity coefficients ∂(Mj)/∂αi provide direct information on the effect of a small perturbation in each parameter about its nominal value on each concentration j, they do not necessarily indicate the effect of simultaneous, large variations in all parameters on each species concentration. An analysis that accounts for simultaneous parameter variations of arbitrary magnitude can be termed a global sensitivity analysis. This type of analysis produces coefficients that have a measure of sensitivity over the entire admissible range of parameter variation. Examples include the “brute force” method, where a single parameter value is changed and the time history of species profiles with and without the modification is compared. Other methods are the FAST method [25], Monte Carlo method [26], and Pattern method [27].The set of equations described by Eqn (2.69) can be rewritten to show the functional dependence of the right-hand side of the equation as
d(Mj)dt=fj[(Mj),ˉα]j=1,…,n
(2.71)
where fi is the usual nonlinear first-order, second-order, or third-order function of species concentrations. The parameter vector ˉα includes all physically definable input parameters of interest (e.g., rate constants, equilibrium constants, initial concentrations, etc.), all of which are treated as constant.
includes all physically definable input parameters of interest (e.g., rate constants, equilibrium constants, initial concentrations, etc.), all of which are treated as constant.For a local sensitivity analysis, Eqn (2.71) may be differentiated with respect to the parameters α to yield a set of linear coupled equations in terms of the elementary sensitivity coefficients, ∂(Mi)/∂αj.
∂∂t(∂(Mj)∂αi)=∂fj∂αi+∑ns=1∂fj∂(Ms)∂(Ms)∂αii=1,…,m
(2.72)
Since the quantities ∂fi/∂(Mj) are generally required during the solution of Eqn (2.71), the sensitivity equations are conveniently solved simultaneously with the species concentration equations. The initial conditions for Eqn (2.72) result from mathematical consideration versus physical consideration as with Eqn (2.71). Here, the initial condition [∂(Mj)/∂αi]t=0
is the zero vector, unless αi is the initial concentration of the jth species, in which case the initial condition is a vector whose components are all zero except the jth component, which has a value of unity. Various techniques have been developed to solve Eqn (2.72) [23,24].
is the zero vector, unless αi is the initial concentration of the jth species, in which case the initial condition is a vector whose components are all zero except the jth component, which has a value of unity. Various techniques have been developed to solve Eqn (2.72) [23,24].It is often convenient, for comparative analysis, to compute normalized sensitivity coefficients
αi(Mj)∂(Mj)∂αi=∂ln(Mj)∂lnαi
(2.73)
αi∂(Mj)∂αi=∂(Mj)∂lnαi
(2.74)
and thus remove any artificial variations to the magnitudes of (Mj) or αi. Thus, the interpretation of the first-order elementary sensitivities of Eqn (2.73) is simply the percentage change in a species concentration due to a percentage change in the parameter αi at a given time t. Since it is common for species concentrations to vary over many orders of magnitude during the course of a reaction, much of the variation in the normalized coefficients of Eqn (2.73) may result from the change in the species concentration. The response of a species concentration in absolute units due to a percentage change in αi as given in Eqn (2.74) is an alternative normalization procedure. For a reversible reaction, the forward and backward rate constants are related to the equilibrium constant. Thus, a summation of elementary sensitivity coefficients for the forward and backward rate constants of the same reaction is an indication of the importance of the net reaction in the mechanism, whereas the difference in the two sensitivity coefficients is an indicator of the importance of the equilibrium constant.
In addition to the linear sensitivity coefficients described above, various other types of sensitivity coefficients have been studied to probe underlying relationships between input and output parameters of chemical kinetic models. These include higher-order coefficients, Green's function coefficients, derived coefficients, feature coefficients, and principal components. Their descriptions and applications can be found in the literature [23,24,28,29].
2.8.2. Rate-of-Production Analysis
A rate-of-production analysis considers the percentage of the contributions of different reactions to the formation or consumption of a particular chemical species.
The normalized production contributions of a given reaction i to a particular species j are given by
Cpji=max(νji,0)qi∑mi=1max(νji,0)qi
(2.75)
The normalized destruction contribution is given by
Cdji=min(νji,0)qi∑mi=1min(νji,0)qi
(2.76)
The function max (x, y) implies the use of the maximum value between the two arguments x and y in the calculation. A similar definition applies to min (x, y). A local reaction flow analysis considers the formation and consumption of species locally; that is, at specific times in time-dependent problems or at specific locations in steady spatially dependent problems [30–32]. An integrated reaction flow analysis considers the overall formation or consumption during the combustion process [30,31]. Here, the results for homogeneous time-dependent systems are integrated over the whole time, while results from steady spatially dependent systems are integrated over the reaction zone. From such results, the construction of reaction flow diagrams may be developed to understand which reactions are most responsible for producing or consuming species during the reaction, that is, which are the fastest reactions among the mechanism.
2.8.3. Coupled Thermal and Chemical Reacting Systems
Since combustion processes generate significant sensible energy during reaction, the species conservation equations of Eqn (2.69) become coupled to the energy conservation equation through the first law of thermodynamics.
If the reaction system is treated as a closed system of fixed mass, only the species and energy equations need to be considered. Consider a system with total mass,
m=∑nj=1mj
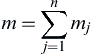(2.77)
where mj is the mass of the jth species. Overall mass conservation yields dm/dt = 0, and therefore the individual species are produced or consumed as given by
dmjdt=V˙ωjMWj
(2.78)
Since the total mass is constant, Eqn (2.78) can be written in terms of the mass fractions:
Yj=mjm=mj∑ns=1ms
(2.79)
Note that ΣYi = 1. The mole fraction is defined as
Xj=njn=nj∑ns=1ns
(2.80)
with ΣXi = 1 (and the n notation referring here to mole number versus reaction order or non-Arrhenius temperature exponent). Mass fractions can be related to mole fractions
Yj=XjMWjMW
(2.81)
where
MW=∑nj=1XjMWj=1∑nj=1(Yj/MWj)
(2.82)
Introducing the mass fraction into Eqn (2.78) yields
dYjdt=˙ωjMWjρj=1,…,n
(2.83)
where ρ = m/V. For a multicomponent gas, the mean mass density is defined by
ρ=∑nj=1(Mj)MWj
For an adiabatic constant-pressure system, the first law reduces to
dh=0
since h = e + Pυ, dh = de + Pdυ, and de = −Pdυ, where υ is the specific volume (V/m). For a mixture, the total enthalpy may be written as
h=∑nj=1Yjhj
(2.84)
and therefore
dhdt=∑nj=1(Yjdhjdt+hjdYjdt)
(2.85)
Assuming a perfect gas mixture,
dhj=cp,jdT
(2.86)
dhdt=∑nj=1Yjcp,jdTdt+∑nj=1hjdYjdt=0
(2.87)
Defining the mass-weighted specific heat of the mixture as
∑nj=1cp,jYj=cp
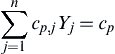(2.88)
and substituting Eqn (2.83) into Eqn (2.87) yields the system energy equation written in terms of the temperature
dTdt=−∑nj=1hj˙ωjMWjρcp
(2.89)
Equations (2.83) and (2.89) form a coupled set of equations, which describe the evolution of species and mixture temperature during the course of a chemical reaction.
The solution procedure to this equation is the same as described for the temporal isothermal species equations described above. In addition, the associated temperature sensitivity equation can be simply obtained by taking the derivative of Eqn (2.89) with respect to each of the input parameters to the model. The governing equations for similar types of homogeneous reaction systems can be developed for constant-volume systems, and stirred and plug flow reactors as described in Chapters 3 and 4 and elsewhere [32–38]. The solution to homogeneous systems described by Eqn (2.83) and Eqn (2.89) are often used to study reaction mechanisms in the absence of mass diffusion. These equations (or very similar ones) can approximate the chemical kinetics in flow reactor and shock tube experiments, which are frequently used for developing hydrocarbon combustion reaction mechanisms.
2.8.4. Mechanism Simplification
As noted in the previous sections, the solution of a chemical kinetics problem in which a large detailed mechanism is used to describe the reaction requires the solution of one species conservation equation for each species of the mechanism. For realistic fuels, the number of species could be very large (several hundred or more), and consequently, the use of such mechanisms in analyzing problems with one or more spatial dimensions can be quite costly in terms of computational time. Thus, methods to simplify detailed reaction mechanisms retaining only the essential features have been under investigation. Simplified mechanisms can also provide additional insight into the understanding of the chemistry by decreasing the complexities of a large detailed mechanism. Steady-state and partial equilibrium assumptions have been used to generate reduced mechanisms [39,40], and sensitivity analysis techniques have been used to generate skeletal mechanisms [24]. An eigenvalue analysis of the Jacobian associated with the differential equations of the system reveals information about the timescales of the chemical reaction and about species in steady state or reactions in partial equilibrium [41]. The eigenvalues can be used to separate the species with fast and slow timescales, and thus, the system may be simplified, for example, by eliminating the fast species by representing them as functions of the slow ones. Examples of such approaches to mechanism simplification are readily available and the reader is referred to the literature for more details [41–46].
Problems
(Those with an asterisk require a numerical solution and use of an appropriate software program—see Appendix I.)
1. For a temperature of 1000 K, calculate the pre-exponential factor in the specific reaction rate constant for (a) any simple bimolecular reaction and (b) any simple unimolecular decomposition reaction following transition state theory.
2. The decomposition of acetaldehyde is found to be overall first-order with respect to the acetaldehyde and to have an overall activation energy of 250 kJ/mol. Assume the following hypothetical sequence to be the chain decomposition mechanism of acetaldehyde:
(1)CH3CHOk1→0.5CH3˙CO+0.5˙CH3+0.5CO+0.5H2
(2)CH3˙COk2→˙CH3+CO
(3)˙CH3+CH3CHOk3→CH4+CH3˙CO
(4)˙CH3+CH3˙COk4→minorproducts
For these conditions,
a. List the type of chain reaction and the molecularity of each of the four reactions.
b. Show that these reaction steps would predict an overall reaction order of 1 with respect to the acetaldehyde.
c. Estimate the activation energy of reaction (2), if El = 335, E3 = 42, and E4 = 21 kJ/mol.
Hint: El is much larger than E2, E3, and E4.
3. Assume that the steady state of (Br) is formally equivalent to partial equilibrium for the bromine radical chain-initiating step and recalculate the form of Eqn (2.39) on this basis.
4. Many early investigators interested in determining the rate of decomposition of ozone performed their experiments in mixtures of ozone and oxygen. Their observations led them to write the following rate expression:
d(O3)/dt=kexp[(O3)2/(O2)]
The overall thermodynamic equation for ozone conversion to oxygen is
2O3→3O2
The inhibiting effect of the oxygen led many to expect that the decomposition followed the chain mechanism
O3+Mk1→O2+O+M
O+O2+Mk2→O3+M
O+O3k3→2O2
a. If the chain mechanisms postulated were correct and if k2 and k3 were nearly equal, would the initial mixture concentration of oxygen have been much less than or much greater than that of ozone?
b. What is the effective overall order of the experimental result under these conditions?
c. Given that kexp was determined as a function of temperature, which of the three elementary rate constants is determined? Why?
d. What type of additional experiment should be performed in order to determine all the elementary rate constants?
5. A strong normal shock wave is generated in a shock tube filled with dry air at standard temperature and pressure (STP). The oxygen and nitrogen behind the shock wave tend to react to form nitric oxide.
Calculate the mole fraction of nitric oxide that ultimately will form, assuming that the elevated temperature and pressure created by the shock are sustained indefinitely. Calculate the time in milliseconds after the passage of the shock for the attainment of 50% of the ultimate amount; this time may be termed the “chemical relaxation time” for the shock process. Calculate the corresponding “relaxation distance,” that is, the distance from the shock wave where 50% of the ultimate chemical change has occurred.
Use such reasonable approximations as: (1) Air consists solely of nitrogen and oxygen in exactly 4:1 volume ratio; (2) Other chemical “surface” reactions can be neglected because of the short times; (3) Ideal shock wave relations for pure air with constant specific heats may be used despite the formation of nitric oxide and the occurrence of high temperature.
Do the problem for two shock strengths, M = 6 and M = 7. The following data may be used:
a. At temperatures above 1250 K, the decomposition of pure nitric oxide is a homogeneous second-order reaction:
k=2.2×1014exp(−39,360K/T)(molcm3)−1s−1
See: Wise, H. and Frech, M. Fr, Journal of Chemical Physics, 20, 22 (1952) and 20, 1724 (1952).
b. The equilibrium constant for nitric oxide in equilibrium with nitrogen and oxygen is tabulated as follows:
| T°(K) | Kp |
| 1500 | 0.00323 |
| 1750 | 0.00912 |
| 2000 | 0.0198 |
| 2250 | 0.0364 |
| 2500 | 0.0590 |
| 2750 | 0.0876 |
See: Gaydon, A.G. and Wolfhard, H.G., “Flames: Their Structure, Radiation and Temperature,” Chapman and Hall, 1970, page 274.
6. Gaseous hydrazine decomposes in a flowing system releasing energy. The decomposition process follows first-order kinetics. The rate of change of the energy release is of concern. Will this rate increase, decrease, or remain the same with an increase in pressure?
7. Consider the hypothetical reaction
A+B→C+D
The reaction as shown is exothermic. Which has the larger activation energy, the exothermic forward reaction or its backward analog? Explain.
8. The activation energy for dissociation of gaseous HI to H2 and I2 (gas) is 185.5 kJ/mol. If the ΔHof,298
for HI is −5.65 kJ/mol, what is the Ea for the reaction H2 + I2 (gas) → HI (gas)?
for HI is −5.65 kJ/mol, what is the Ea for the reaction H2 + I2 (gas) → HI (gas)?9. From the data in Appendix C, determine the rate constant at 1000 K for the reaction
H2+OHkf→H2O+H
10. Consider a reacting mixture of hydrogen and oxygen. Knowing that the product water is formed through the chemical reaction of Problem 9, find an expression for the rate of formation of the water vapor assuming all the radicals to be partially equilibrated among a subset of reactions.
11. Consider the first-order decomposition of a substance A to products. At constant temperature, what is the half-life of the substance?
12. ∗A proposed mechanism for the reaction between H2 and Cl2 to form HCl is given below.
Cl2+M⇄Cl+Cl+M
H2+M⇄H+H+M
H+Cl2⇄HCl+Cl
Cl+H2⇄HCl+H
H+Cl+M⇄HCl+M
Calculate and plot the time-dependent species profiles for an initial mixture of 50% H2 and 50% Cl2 reacting at a constant temperature and pressure of 800 K and 1 atm, respectively. Consider a reaction time of 200 ms. Perform a sensitivity analysis and plot the sensitivity coefficients of the HCl concentration with respect to each of the rate constants. Rank order the importance of each reaction on the HCl concentration. Is the H atom concentration in steady state?
13. ∗High-temperature NO formation in air results from a thermal mechanism (see Chapter 8) described by the following two reactions:
N2+O⇄NO+N
N+O2⇄NO+O
Add to this mechanism the reaction for O2 dissociation
O2+M⇄O+O+M
and calculate the time history of NO formation at a constant temperature and pressure of 2500 K and 1 atm, respectively. Develop a mechanism that has separate reactions for the forward and backward directions. Obtain one of the rate constants for each reaction from Appendix C and evaluate the other using the thermodynamic data of Appendix A. Plot the species profiles of NO and O as a function of time, as well as the sensitivity coefficients of NO with respect to each of the mechanism rate constants. What is the approximate time required to achieve the NO equilibrium concentration? How does this time compare to residence times in flames or in combustion chambers?
..................Content has been hidden....................
You can't read the all page of ebook, please click here login for view all page.