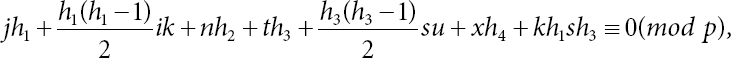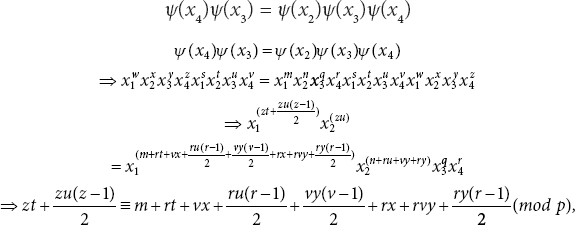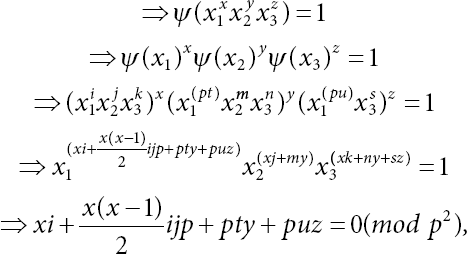20
Automorphisms of Some Non-Abelian p−Groups of Order p4
Muniya Sansanwal1⋆, Harsha Arora2 and Mahender Singh3
1Department of Mathematics, JJTU Jhunjhunu, Rajasthan, India
2Department of Mathematics, Govt. College for Women Hisar, Haryana, India
3Department of Mathematics, Om Sterling Global University, Hisar, Haryana, India
Abstract
This paper contains the number of automorphisms of several non-Abelian groups of order p4, p-odd prime are computed and GAP (Group Algorithm Programming) software has been used for the verification of a number of automorphisms.
Keywords: -p-groups, automorphism, semi-direct product
MSC subject classification 2000: 20D45, 20D60
20.1 Introduction
Let G be a p-group of order p4, p-odd prime and Aut(G) represent the group of all automorphisms of a given group G. There are many research papers in the literature related to the automorphisms of p-groups, for instance [1, 3, 4], etc. In [1], the automorphisms of groups of order p3 are computed along with the automorphisms of abelian groups of order p4. The present paper is an extension of the research work in [1]. In this paper, we will compute the automorphisms of groups of order p4. William Burnside [2] classified all groups having order p4. By using these classifications we derive the automorphisms of some groups having order p4. We divide the derived results into two parts. In these two parts, one part is dedicated to the categorization of all p−groups of order p4 and the other part is dedicated to investigating the number of automorphisms of several non-Abelian groups with order p4.
20.2 Categorization of p-Groups with Order p4
According to the categorization derived by Burnside [2], if p is an odd prime, then there will be 15 groups of order p4. Five of these are abelian and the rest are non-abelian, as given below.
Abelian Groups:

Non-Abelian Groups:

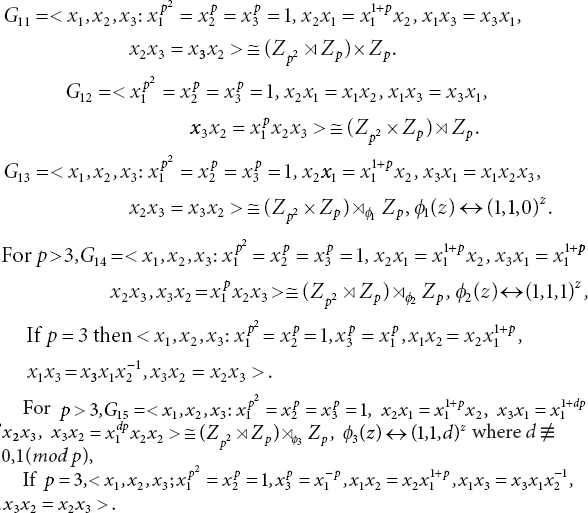
20.3 Number of Automorphisms of Some Non-Abelian Groups of Order p4
The automorphisms of five abelian groups, namely G1, G2, G3, G4, and G5, of order p4 are already computed in the paper [1]. In this paper, we compute the automorphisms of several non-abelian p−groups with order p4, namely G9, G10, and G11 denoted above.
20.3.1 Computation of Automorphisms of Group G9

We can deduce relations by using generator relations from the structure description of G9 and elementary calculations:

Now, we shall investigate the automorphism group ![]()
Let ![]() be defined by:
be defined by:

As ψ is automorphism, ψ should preserve the relation x2x1x3 = x3x1, that is
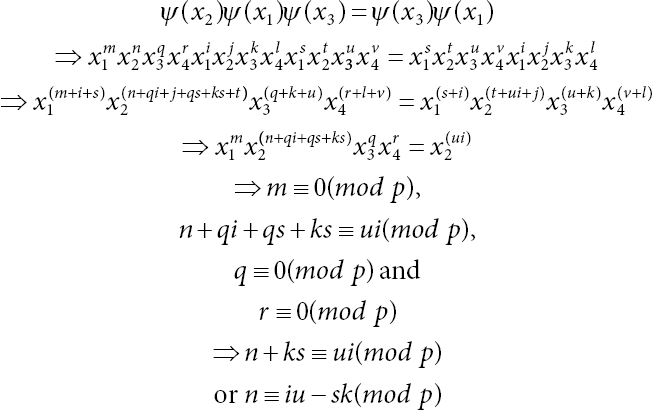
As n ≢ 0(mod p), because if n ≡ 0(mod p) then order of (ψ(x2)) ≠ p.
Also, x4x3 = x3x4 then ψ(x4)ψ(x3) = ψ(x3)ψ(x4)

Further, x1x4 = x4x1 implies ψ(x1)ψ(x4) = ψ(x4)ψ(x1)
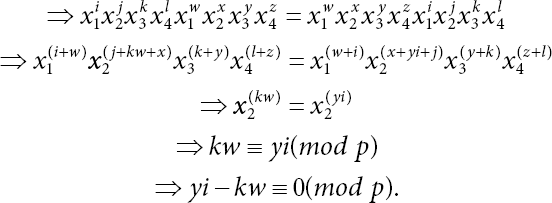
Now, ys − uw ≡ 0(mod p) and yi − kw ≡ 0(mod p) are two homogeneous equations with determinant iu − sk ≠ 0. Hence, these equations have only trivial solutions. ⇒ y = w ≡ 0(mod p).
Next, we check the kernel of ψ. Let ![]() be any element of
be any element of ![]() so that it is mapped to identity.
so that it is mapped to identity.
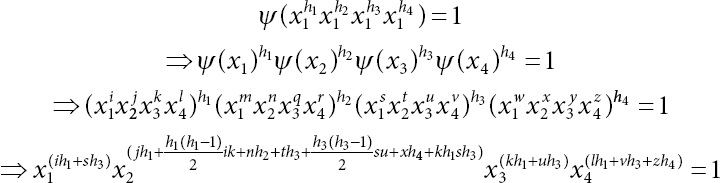
Equations (20.1) and (20.3) are the system of two homogeneous equations with iu − sk ≠ 0 determinant, which gives only a trivial solution. Hence, h1 = h3 = 0. From (20.4), we get
As
we get
Further, from (20.2) we get nh2 ≡ 0(mod p), but n ≢ 0(mod p) ⇒ h2 = 0. So, if ![]() and ψ(h) = 1, it must be that h = 1.
and ψ(h) = 1, it must be that h = 1.
Hence, the kernel is trivial and ψ is an automorphism with the constraints on the parameters already deduced. Now it is very easy to calculate the order of the automorphism group. We have p choices for all j, l, t, v, x, and p − 1 choices for z and i, u, s, and k will in some sense be equivalent to a matrix in GL(Fp), which gives (p2 −p)(p2 − 1) choices for the elements. Therefore, we have that ![]() is really defined as:
is really defined as:
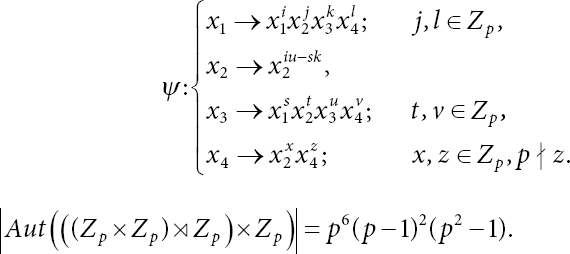
20.3.2 Computation of Automorphisms of Group G10

By using our relations from the structure of G10 and elementary calculations, we can deduce some useful relations:
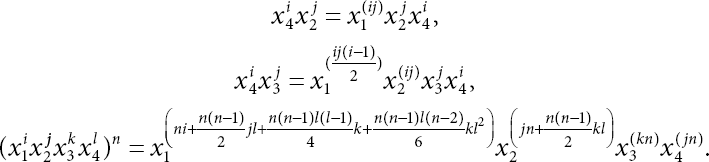
We begin our study of automorphism group ![]() by using the above relations.
by using the above relations.
Let ![]() be defined by:
be defined by:

Since ψ is an automorphism, ψ should preserve the relation x4x3 = x2x3x4, hence
using (20.7) and (20.8) in (20.5) and (20.6), we get
Also,
Using Equations (20.13) and (20.14) in (20.11) and (20.12), we get
Since j, k, l ≡ 0(mod p), therefore i ≢ 0(mod p) because if i ≡ 0(mod p), then Ord(x1) ≠ p. Further, from (20.15), i = zn ≢ 0(mod p), we have z ≢ 0(mod p) and n ≢ 0(mod p).
Next, we have x2x3 = x3x2

Now, n ≢ 0(mod p) gives v ≡ 0(mod p)
From (20.10), we can see zu ≡ n + vy(mod p), therefore zu ≡ n(mod p) or n ≡ zu(mod p).
Also, from (20.15) i ≡ zn(mod p), we get i ≡ zzu(mod p). Thus, we have
Further, as n ≡ zu(mod p) and n ≢ 0(mod p), therefore u ≢ 0 (mod p). Substituting the value of v in (20.9), we get ![]()
![]() Now, we shall find the constraints on the parameters for which ψ has a trivial kernel. Let
Now, we shall find the constraints on the parameters for which ψ has a trivial kernel. Let ![]()
From (20.20), we have h4 ≡ 0(mod p) for z ≢ 0(mod p) and from (20.19), we get uh3 ≡ 0(mod p). Since u ≢ 0(mod p), therefore h3 = 0. Further, from (20.18), we have nh2 ≡ 0(mod p). As n ≢ 0(mod p), we have h2 = 0. From (20.17), ih1 ≡ 0(mod p), but i ≢ 0(mod p), thus h1 = 0.
So, if ![]() and ψ(h) = 1, it must be that h = 1, hence the kernel is trivial and ψ is an automorphism with the constraints we have already deduced. Thus, for ψ to be an automorphism there are p choices for all s, t, w, x, y, and p − 1 choices for both u and z. Therefore, we have that
and ψ(h) = 1, it must be that h = 1, hence the kernel is trivial and ψ is an automorphism with the constraints we have already deduced. Thus, for ψ to be an automorphism there are p choices for all s, t, w, x, y, and p − 1 choices for both u and z. Therefore, we have that ![]() is really defined as:
is really defined as:
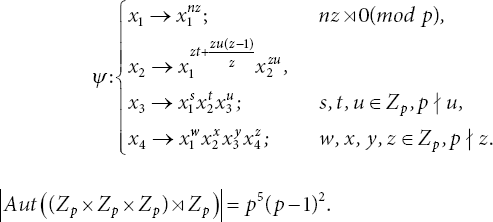
20.3.3 Computation of Automorphisms of G11
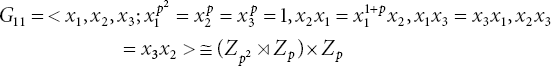
We can deduce some useful relations by using the generator relations of G11 and elementary calculations:

With these relations, we begin our study of the automorphisms of ![]()
Let ![]() be defined by:
be defined by:

Now, ord(x1) = ord(ψ(x1)) = p2.
Therefore, ![]()
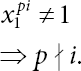
Also, the order of ![]() is p, so the order of ψ(x2) is
is p, so the order of ψ(x2) is

Order of x3 is also p, so Order of ψ(x3) is p

As ψ is an automorphism, ψ should preserve the relation ![]() thus we get
thus we get

Next, we find the constraints for parameters using the kernel. Let ![]() be any element of
be any element of ![]() that it is mapped to identity.
that it is mapped to identity.
From (20.21), we get
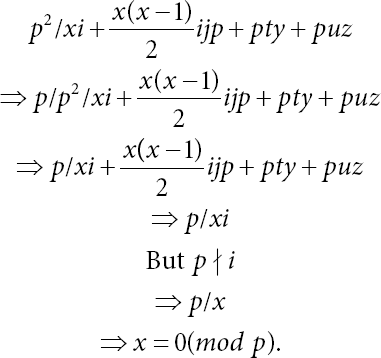
Next, from (20.22) we have

Also, from (20.23) we obtain sz ≡ 0(mod p), but p f s, therefore z ≡ 0(mod p).
So, if ![]() and ψ(h) = 1, it must be that h = 1, hence the kernel is trivial and ψ is an automorphism with the restrictions we have already deduced on the parameters. Now, we have here p2 − p choices for i and p choices for all l, q, j, k, n, and p − 1 choices for s. Therefore, we have that
and ψ(h) = 1, it must be that h = 1, hence the kernel is trivial and ψ is an automorphism with the restrictions we have already deduced on the parameters. Now, we have here p2 − p choices for i and p choices for all l, q, j, k, n, and p − 1 choices for s. Therefore, we have that ![]() is really defined as:
is really defined as:

References
- 1. H. Arora and R. Karan: What is the probability an automorphism fixes a group element?, Communications in Algebra, 45(3), 1141–1150 (2017).
- 2. William Burnside: Theory of groups of finite order, Cambridge University Press, first edition, 1897. Reprinted 2010 through Nabu Press.
- 3. Geir T. Helleloid Automorphism Groups of Finite p-Groups: Structure and Applications, arxiv: 0711.2816 (2007).
- 4. Hans Liebeck: The Automorphism Group of finite p-groups, Journal of Algebra, 4, 426–432 (1966).
Note
- ⋆ Corresponding author: [email protected]