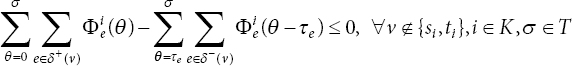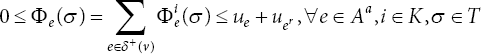Abstract

Routing multiple distinct commodities from particular supply points to appropriate destination points via the arcs of a network topology while preserving capacity limits is the most challenging issue in operations research. The quickest multi-commodity flow issue reduces the delivery time to complete the process. Computationally, this problem is NP-hard. We consider asymmetric transit times on anti-parallel lanes due to uneven road conditions and flow dependency. Outbound lane capacity can be boosted by reorienting lanes towards demand locations. We incorporate the contraflow strategy to the quickest multi-commodity flow problem and provide an approximation scheme utilizing length-bounded flow with non-symmetric traversal times on oppositely oriented lanes.

Keywords: Network flow, quickest multi-commodity, contraflow, non-symmetric traversal times, length-bound

16.1 Introduction

The topology of a transport system is described as a network that correlates to the transshipment of diverse commodities, with distribution centers, demand centers, and intersections of road segments serving as nodes and arcs serving as linkages between nodes. The starting and ending destinations of commodities are known as supply points and demand points, respectively. Flow refers to the collection of goods that have been transported via the network. In networks with temporal dimensions capacity and travel times are allocated to the arcs. For more details, we refer to [1−5].

The multi-commodity network flow problem entails transporting several commodities from specified delivery sites to appropriate destination points while staying within arc capacity restrictions. Static flow and dynamic flow are two types of flow that can occur in this scenario. Maximum, maximum concurrent, and least cost flow issues are the three categories of static flow problems. Maximum flow issues emerge when the aggregate of all commodity flows is maximized. The maximum flow problem wherein the proportion of total demand is maximized is a maximum concurrent flow problem.

The minimal cost flow problem is described as determining the flow value that meets all commodity demands at the lowest cost while adhering to capacity constraints on all arcs. Furthermore, dynamic multi-commodity flow problems may be classified as maximal dynamic, quickest, minimum cost, and earliest arrival flow problems (see [4−8]).

Ford and Fulkerson [9] are credited with inventing network flow over time in the late 1950s. In the theory of supply and demand, the aim is to compute the quickest way to fulfill the needs for something, i.e., to get it from origin to destination is the quickest flow problem.

The first polynomial-time bound was computed by Burkard et al. [10] for this problem using a binary search. They reduced the complexity and gave strong polynomial-time bounds with the help of a parametric search. The quickest transshipment problem is one in which a flow of commodities fulfills all supplies and demands in the least amount of time.

Authors in [11] generalize the naive method to solve a dynamic flow problem to the situation of multi-commodities. Furthermore, the authors used length-bounded static flows instead of methodology, which used a static minimal cost flow computation. Even though static flows do not contain a time component, Fleischer and Skutella [11] looked at flows that offer feasible routes using travel time as a measure of length. They divide static flows into pathways, with each path starting at an origin node and ending at a corresponding destination node. Multi-commodity flow problems are more difficult than single-commodity flow problems, even in graphs with series-parallel composition or with only two commodities. The author in [12] found that the flow of several commodities over time is NP-hard. NP-hardness exists in multiple products with and without intermediate node storage for the quickest flow problem with a simple flow path. Because this issue is NP-hard, two techniques to obtain an approximate solution have been presented in [11, 13].

Lozovanu et al. [14] and Kappmeir [15] used a time expansion approach for solving the maximum dynamic multi-commodity flow problem. This approach is extended to multiple sources and a single sink multi-commodity earliest arrival transshipment in [15].

Contraflow refers to the switching arc orientations to boost traffic flow value and minimize traversal time by increasing the capacity of lanes in a network. For a single-source and a single-sink, the authors in [16] proposed models and strongly polynomial-time methods to solve maximum and quickest flow problems. At time zero, these contraflows are made and then rectified. Nath et al. [17] investigated the problem with asymmetric traversal times on oppositely directed lanes and modified the algorithm of [16] so that traversal time of a non-reversed arc is taken after lane reversals and solved the problem in polynomial-time for a single-commodities. In [18], the authors reported a polynomial-time solution to the earliest arrival transshipment problem and the maximum flow problem with priority on terminals. Gupta et al. [19] investigated the non-polynomial solution of the generalized maximum flow issue on a lossy network with non-symmetric traversal times on anti-parallel lanes. Recently, the authors in [20] extended this to the case of multi-commodity with symmetric transit times and the same authors in [21] provided FPTAS to a maximum dynamic multi-commodity contraflow problem with non-symmetric traversal times on oppositely oriented lanes.

The fundamental objective of partial contraflow is to use the capacity of underutilized lanes and was introduced by Pyakurel et al. [22]. In times of emergency, the stored capacity of unoccupied arcs might be utilized for logistical assistance and facility placement.

We present the quickest multi-commodity contraflow (QMCCF) problem with non-symmetric traversal times on anti-parallel lanes in this paper. Fleischer and Skutella [11, 13] developed an approximation algorithm to this problem without contraflow using a T-length bounded function.

The authors in [23, 24] introduced a partial lane reversal approach with symmetric traversal times on oppositely directed lanes. We provide the polynomial-time approximate solution of the problem by utilizing a T-length bound approximation. The travel time for transshipping commodities from origin nodes to destination nodes is reduced by using the lane reversal strategy in the routing problem. The study’s main relevance is the decrease in delivery time.

The rest of the article is arranged as follows. Section 16.2 describes fundamental concepts with flow models. The QMCCF problem with non-symmetric traversal times on oppositely oriented lanes is introduced in Section 16.3. We provide a method for solving the issue in polynomial-time in this section. The final portion concludes the paper.

16.2 Preliminaries with Flow Models

The multi-commodity flow problem entails distributing several commodities from their origin-destination pairs across a specified network to meet the entire demand for each commodity. We define the basic notations and provide mathematical formulations for this problem, in which arc reversals are allowed to optimize the objective value by reverting their directions as needed.

16.2.1 Mathematical Model with Contraflow

Suppose a network architecture N = (V, A, K, u, τ, d_i, S⁺, S⁻, T) is composed of a collection of nodes V and arcs A. The collection of commodities is denoted by K = {1, 2,..., k}, with |V | = n and |A| = m. The demand d_i is set and it is delivered via a particular origin-destination path s_i-t_i, where s_i ∈ S⁺ and t_i ∈ S⁻, ∀i ∈ K. The capacity function u: A → R⁺ regulates the flow and traversal time function. τ: A → R⁺ computes the time it takes to carry the flow on each arc, e. In discrete and continuous-time contexts, the time period T is indicated as T = {0, 1,..., T} and T = [0, T], respectively. The sets δ⁺(v) = {e: e = (v,. ) |., ∈ V} and δ⁻(v) = {e: e,= (., v) |., ∈ V } represent a set of arcs moving out from v and entering into v, respectively, so that δ⁺(S⁻) = δ⁻(S⁺) = ∅ besides contraflow network.

The auxiliary network for network N is represented by N^a = (V, A^a, K, u^a, τ^a, d_i, S⁺, S⁻, T), with the edges having no direction. The arc e^r represents the backward arc of e. The capacity is re-defined as the total of the capacities of the anti-parallel lanes, in N^a with u_e = 0, if e ∉A. The traversal time τ_a along with arc a in N^a is the same as the traversal time of non-reversed arcs. For a single lane, we assume Other network parameters

are unaltered.

A static network is one that lacks a time dimension and is defined by N,= (V, A, K, u, d_i, S⁺, S⁻).

The static flow function is defined by x: A → R⁺. To compute the solution of real world dynamic flow problems, many useful properties of static network topology are essential tools. A multi-commodity flow over time Φ in a network N with contraflow is a collection of commodities described by Φⁱ: A^a × T → R⁺ meeting the requirements (16.2−16.4).

(16.1)

subject to,

(16.2)

(16.3)

(16.4)

In this case, the third equation in constraint (16.2) denotes flow conservation restrictions at time T, but the constraints in (16.3) denote non-conservation needs at intermediate time points T. Likewise, capacity with lane reversals limits the bundle restrictions in (16.4). The purpose is to deliver a predetermined quantity of flow to fulfill the demand for each commodity from supply points to destination locations in the least amount of time, as specified by the first two conditions of (16.2).

The cost is defined by

(16.5)

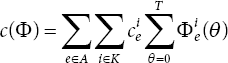
The cost bound for each commodity i is determined as:

(16.6)

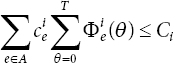
Example 1. Suppose a two-commodity network, as illustrated in Figure 16.1(a), has capacity and travel times on arcs. The pathways s₁ − t₁ and s₂ − t₂ are used to transport the first and second commodities, respectively. A contraflow network is depicted in Figure 16.1(b).

Authors in [25] modeled the quickest contraflow problem for a single commodity as an integer programming problem. Furthermore, they proposed greedy and bottle-neck relaxation heuristics to provide a numerical solution. Rebennack et al. [16] presented its polynomial-time solution. However, the problem with numerous sources and/or sinks is NP-complete via a reduction from 3-SAT [16]. In [26, 27], the continuous-time variant of a single-source single-sink maximum and the quickest contraflow problems are polynomially solvable. The authors in [22] introduced and solved the problem with partial lane reversals.

16.3 QMCCF with Non-Symmetric Transit Times

The lane reversal approach for the QMCCF problem with non-symmetric traversal times on oppositely oriented lanes is discussed in this section. In a network architecture where arc reversals are allowed, a solution to this problem meets given demands at defined nodes in the shortest time feasible.

We present a polynomial-time approximation scheme (PTAS) to compute the solution. Furthermore, our technique may be used to save lanes that do not need to be reversed to shorten the time. Instead of symmetric traversal times on oppositely oriented lanes in [23, 24], we consider asymmetric traversal times on oppositely oriented lanes and present Problem 1.

Problem 1. Assume a network N = (V, A, K, u, τ, S⁺, S⁻, d_i, T) has non-symmetric traversal times on oppositely oriented lanes. The QMCCF problem aims to find the minimum feasible time that meets the requirements (16.2), (16.3), and (16.4) to transport a specified number of demands d_i, ∀i ∈ K from supply points to corresponding destination points at a bounded cost by reverting the orientation of only essential arcs from the beginning.

Even with a series-parallel network composition or network having two commodities only, the multi-commodity flow over time problem is NP-hard [12]. The proof is based on reductions from the NP-hard PARTITION and 3-PARTITION issues. In addition, the problem of maximal multi-commodity flow with no limits on intermediate node storage is NP-hard. A time expansion is a tool that provides the pseudo-polynomial time solution.

The same hardness exists to the quickest multi-commodity flow problem having a simple path and without intermediary node storage according to [12].

Authors in [25] used 3-SAT to show that lane reversal is NP-complete. As a result, we have Theorem 1.

Theorem 1. The QMCCF problem with bounded cost having asymmetric traversal times on anti-parallel arcs is NP-hard.

As the quickest multi-commodity flow problem is NP-hard, two techniques are proposed to provide an approximate solution in [13]. One is the discretization of bigger time steps as opposed to single time steps, while the other is the length-bounded flow.

The authors in [23, 24] incorporated partial lane reversals with equal traversal times on oppositely oriented lanes and provided the solution using the same approach. We consider non-symmetric traversal times on oppositely oriented lanes and provide a PTAS to Problem 1 with the help of length-bounded flow.

16.3.1 Approximation Approach for the QMCCF

A single or multi-commodity path flow is considered as a length-bounded flow, where each used path is subjected to a length restriction. Let P_i represent the sum of all s_i − t_i routes ∀i ∈ K in the network N^a. A static flow x is known as a T-length bounded if every constituent flow xⁱ for each i ∈ K can be broken down into the amount of flows , i.e., with and the length of any path P ∈ Pi is at most T. A T-length, restricted static flow x that matches multi-commodity constraints is NP-hard to discover [13]. This issue, on the other hand, is polynomial-time approximated.

We compute an approximate solution to the QMCCF problem with non-symmetric traversal times on anti-parallel lanes by applying length-bounded flows as described [23, 24] and presented in Algorithm 1. In Step 2 of our approach, we first review the solution technique of [11, 13]. All other steps of the algorithm are feasible according to [23]. The removal of the cycle flow in Step 3 suggests that flow only travels in one direction, not both. In Step 5, the capacity of the unutilized arcs is preserved. We argue that a possible approximate solution to the QMCCF with non-symmetric traversal time on oppositely oriented lanes on network N would likewise be a feasible approximate solution to the quickest multi-commodity flow issue on modified network N^a.

The authors in [17] have shown that the complexity of the lane reversal problems having non-symmetric travel times on oppositely oriented lanes is the same as symmetric travel time on oppositely oriented lanes. As a result, an approximate QMCCF with non-symmetric traversal time on oppositely oriented lanes may be optimally calculated on network N. Hence, we have Theorem 2.

Theorem 2. An approximate solution to the QMCCF problem with non-symmetric traversal times on oppositely oriented lanes can be determined in polynomial-time by using T-length bound.

Example 2. Consider a network as illustrated in Figure (16.1)(a) with two commodities having demands d₁ = 12 and d₂ = 8. The quickest time without contraflow with symmetric and asymmetric traversal times on lanes can be computed by using Figure 16.1(a), and the quickest time with contraflow having symmetric and asymmetric traversal times on lanes can be computed by using Figure 16.1(b), respectively.

There is only one path for commodity-1 from s₁ to t₁ and only one path for commodity-2, i.e., s₂ to t₂ before contraflow with symmetric or asymmetric traversal times (cf. Figure 16.1(a)). A 5-length bound is required for computing the solution of Problem 1 to the quickest multi-commodity without contraflow having symmetric traversal times (cf. Figure 16.1(a)), and it is repeated four times. As a result, T₁ = 8 units of time are required to meet the indicated demand d₁ = 12 of commodity-1. Similarly, a 5-length bound is required and is repeated four times for commodity-2. As a result, it takes T₂ = 8 units of time to meet demand d₂ = 8 of commodity-2. Hence, the shortest possible time needed to fulfill both needs is T = max{T₁, T₂} = {8, 8} = 8. If we take asymmetric traversal times on oppositely oriented lanes before contraflow (cf. Figure 16.1(a)), a 4-length bound is essential to meet the demand of commodity-1 and it is repeated 4-times. So, T₁ = 7 is the shortest time needed to fulfill the demand of commodity-1. Similarly, a 4-length bound is essential to meet the need of commodity-2 and it is repeated 4-times. So, to fulfill the need of commodity-2, T₂ = 7 is the quickest time. Hence, the shortest possible time needed to fulfill both needs is T = max{T₁, T₂} = {7, 7} = 7.

However, if contraflow is used (see Figure 16.1(b)), and traversal time is symmetric, the time taken to meet both needs is T = 6 units.

In the same way, if lane reversal is used (see Figure 16.1(b)), and traversal time is non-symmetric on oppositely oriented lanes, it requires T = 5 units of time to meet both demands. Thus, contraflow with symmetric traversal times saves approximately 25 percent of the time, whereas contraflow with non-symmetric traversal times on oppositely oriented lanes saves approximately 28.7 percent of the time.

Table 16.1 and Table 16.2 summarize the data obtained from Example 2.

LB without contraflow ST	LB without contraflow AT
8	7

LB with contraflow ST	LB with contraflow AT
6	5

LB=length bound, ST=symmetric transit times, AT=asymmetric transit times.

16.4 Conclusions

One of the primary issues in operations research is routing many commodities from their delivery points to target points over a shared network. A crucial concern is the reduction of time (cost). A well-known quickest flow problem was addressed to deliver the requisite demand in the shortest feasible period. For a single-commodity, this issue was solved in strongly polynomial-time, but for several commodities it is NP-hard. However, a polynomial-time approximation technique based on a length-bounded function was found. The lane reversals technique is an essential tool for improving the quickest time in the two-way network. We incorporated this approach in length-bounded approximation.

In this work, we investigated the QMCCF problem with non-symmetric traversal times on oppositely oriented lanes. We presented its mathematical model and provided a polynomial-time approximation algorithm. This study minimizes the routing time significantly. By analyzing the results of the previously studied problem with constant transit time, it would be interesting to extend these strategies to flow-dependent transit times. The findings in this research have both theoretical and practical implications.

Acknowledgments

The first author wishes to thank the University Grant Commission of Nepal for the Ph.D. research grant and the second author wishes to thank the Alexander Von Humboldt Foundation for the Digital Cooperation Fellowship (August 1, 2021 to January 31, 2022).

References

1. 1. R. K. Ahuja, T. L. Mangati, and J. B. Orlin, Network flows: theory, algorithm, and applications, Prentice Hall, Englewood Cliffs, 1993.
2. 2. A. Assad, Multi-commodity network flows a survey, Networks, Vol. 8(1), pp. 37-91, 1978.
3. 3. J. Kennington, A survey of linear cost multi-commodity network flows, Operations Research, Vol. 26(2), pp. 209-236, 1978.
4. 4. K. Salimifard and S. Bigharaz, The multi-commodity network flow problem: state of the art classification, applications, and solution methods, Springer, pp. 1-47, 2020.
5. 5. I.-L. Wang, Multi-commodity network flows: A survey, part I: Applications and formulations, International Journal of Operations Research, Vol. 15(4), pp. 145-153, 2018.
6. 6. A. Ali, R. Helgason, J. Kennington, and H. Lall, Computational comparison among three multi-commodity network flow algorithms, Operations Research, Vol. 28(4), pp. 995-1000, 1980.
7. 7. J. A. Tomlin, Minimum cost multi-commodity network flows, Operational Research, Vol. 14, pp. 45-51, 1966.
8. 8. U. Pyakurel, S. P. Gupta, D. P. Khanal, and T. N. Dhamala, Efficient algorithms on multi-commodity flow over time problems with partial lane reversals, International Journal of Mathematics and Mathematical Sciences, Hindawi, pp. 1-13, 2020. Article ID 2676378, https://doi.org/10.1155/2020/2676378.
9. 9. L. R. Ford and D. R. Fulkerson, Flows in networks, Princeton University Press, Princeton, New jersey, 1962.
10. 10. R. E. Burkard, K. Dlaska, and B. Klinz, The quickest flow problem. ZOR-Methods and Models of Operations Research, Vol. 37, pp. 31-58, 1993.
11. 11. L. Fleischer and M. Skutella, The quickest multicommodity flow problem, In International Conference on Integer Programming and Combinatorial Optimization, Springer, pp. 36-53, 2002.
12. 12. A. Hall, S. Hippler, and M. Skutella, Multi-commodity flows over time: efficient algorithms and complexity. Science Direct, Vol. 379, pp. 387-404, 2007.
13. 13. L. Fleischer and M. Skutella, Quickest flows over time, SIAM Journal on Computing, Vol. 36(6), pp. 1600-1630, 2007.
14. 14. D. Lozovanu and M. Fonoberova, Optimal dynamic multicommodity flows in networks, Electron Notes Discrete Math, Vol. 25, pp. 93-100, 2006.
15. 15. P. W. Kappmeier, Generalizations of flows over time with application in evacuation optimization, PhD Thesis, Technical University, Berlin, Germany, 2015.
16. 16. S. Rebennack, A. Arulselvan, L. Elefteriadou, and P. M. Pardalos, Complexity analysis for maximum flow problems with arc reversals, Journal of Combinatorial Optimization, Vol. 19, pp. 200-216, 2010.
17. 17. H. N. Nath, U. Pyakurel, and T. N. Dhamala, Network reconfiguration with orientation dependent transit times, International Journal of Mathematics and Mathematical Sciences, Hindawi, pp. 1-11, 2021. Article ID 6613622, https://doi.org/10.1155/2021/6613622.
18. 18. S. P. Gupta, U. Pyakurel, and T. N. Dhamala, Network flows with arc reversals and non-symmetric transit times, American Journal of Mathematics and Statistics, Vol. 11(2), pp. 27-33, 2021.
19. 19. S. P. Gupta, U. Pyakurel, and T. N. Dhamala, Generalized dynamic contraflow with non-symmetric transit times, American Journal of Computational and Applied Mathematics, Vol. 11(1), pp. 12-17, 2021.
20. 20. S. P. Gupta, U. Pyakurel, and T. N. Dhamala, Multi-commodity flow problem on lossy network with partial lane reversals. Annals of Operations Research (ANOR), 323(1-2), 45-63, 2023, https://doi.org/10.1007/s10479-023-05210-y
21. 21. S. P. Gupta, U. Pyakurel, and T. N. Dhamala, Dynamic multi-commodity contraflow problem with asymmetric transit times, Journal of Applied Mathematics, Hindawi, pp. 1-8, 2022. Article ID 3697141, https://doi.org/10.1155/2022/3697141.
22. 22. U. Pyakurel, H. N. Nath, S. Dempe, and T. N. Dhamala, Efficient dynamic flow algorithms for evacuation planning problems with partial lane reversal, Mathematics, Vol. 7, pp. 1-29, 2019.
23. 23. T. N. Dhamala, S. P. Gupta, D. P. Khanal, and U. Pyakurel, Quickest multi-commodity flow over time with partial lane reversals, Journal of Mathematics and Statistics, Vol. 16(1), pp. 198-211, 2020.
24. 24. S. P. Gupta, D. P. Khanal, U. Pyakurel, and T. N. Dhamala, Approximate algorithms for continuous-time quickest multi-commodity contraflow problem, The Nepali Mathematical Sciences Report, Vol. 37(1-2), pp. 30-46, 2020.
25. 25. S. Kim, S. Shekhar, and M. Min, Contraflow transportation network reconfiguration for evacuation route planning, IEEE Trans. Knowl. Data Eng., Vol. 20, pp. 1115-1129, 2008.
26. 26. U. Pyakurel and T. N. Dhamala, Evacuation planning by earliest arrival contraflow, Journal of Industrial and Management Optimization, Vol. 13, pp. 487-501, 2017.
27. 27. U. Pyakurel, T. N. Dhamala, and S. Dempe, Efficient continuous contraflow algorithms for evacuation planning problems. Annals of Operations Research (ANOR), Vol. 254, pp. 335-364, 2017.