18
An Amended Moth Flame Optimization Algorithm Based on Fibonacci Search Approach for Solving Engineering Design Problems
Saroj Kumar Sahoo⋆ and Apu Kumar Saha
Department of Mathematics, National Institute of Technology Agartala, Tripura, India
Abstract
The moth flame optimization (MFO) algorithm is a swarm intelligence (SI) based algorithm which gained popularity among researchers due to a special kind of movement mechanism, namely, a transverse orientation mechanism of the moth in nature. Like other SI based algorithms, it also suffers from good quality solution and slow convergence speed. To avoid the drawbacks, a new variant of MFO algorithm, namely, a Fibonacci technique based MFO algorithm (in short Ft-MFO) is presented in this paper. We merged the concept of Fibonacci search method in the classical MFO algorithm to improve the search quality and accelerate the convergence speed of the MFO algorithm. To validate the performance of the proposed algorithm, Ft-MFO is compared with six popular stochastic optimization algorithms on an IEEE CEC2019 test suite and two constraint engineering design problems. Experimental results demonstrate that the proposed Ft-MFO algorithm is superior to the other stochastic algorithms in terms of solution quality and convergence rate.
Keywords: Moth flame optimization algorithm, Fibonacci search method, benchmark functions
18.1 Introduction
The challenge of finding the better solution in optimization problems is an interesting topic of research due to its importance in both academia and industry. If the number of optimization parameters increases, the optimization problem complexity also increases. In recent decades, researchers are very much interested in machine learning and artificial intelligence (AI) techniques as real-life difficulties, such as constrained or unconstrained, linear or nonlinear, continuous or discontinuous, that can be easily tackle by AI and machine learning techniques [1, 2]. Due to the aforementioned characteristics, there are various levels of difficulty to handle such types of difficulties using conventional techniques through numerical or mathematical programming, namely quasi-Newton approach, quadratic programming, conjugate gradient, fast steepest method [3], etc. In various existing research [4], it has been experimentally proved that the above-mentioned approaches are not efficient enough to handle non-differentiable and real-life multimodal issues. In contrast, the nature-based algorithms have played a substantial role in tackling these issues, as these algorithms are simple and can be easily applied. A few of them are the Genetic Algorithm (GA) [5], Particle Swarm Optimizer (PSO) [6], Differential Evolution (DE) [7], Spotted Hyena Optimization Algorithm (SHO) [8], Butterfly Optimization Algorithm (BOA) [9], Whale Optimization Algorithm (WOA) [10], Sine Cosine Algorithm (SCA) [11], Moth Flame Optimizer (MFO) [12], Salp Swarm Algorithm (SSA) [13], etc. Typically, these algorithms initiate by a set of randomly chosen initial solutions and continue until they get the optimal solution of a problem. When the algorithm exceeds the pre-determined number of iterations it will automatically be terminated. There is an increasing interest for the efficient, low-cost, and effective implementation of such metaheuristic algorithms these days.
The MFO algorithm is the subject of this article. In 2015, Mirjalili discovered MFO, a swarm intelligence-based algorithm. Transverse orientation is used by moths to navigate in the wild and served as an inspiration for MFO. Spiral flight search and simple flame generation (SFG) are two of the most important MFO tactics. In the SFG technique, the best moths and flames collected thus far can be used to directly manufacture flames. By following moths’ transverse direction, the SFS technique allows moths to spiral toward the flames to update the positions in an iterative way. It is possible that MFO will find the best option in the available search space. The transverse orientation of moths in particular is critical to the effectiveness of MFO. The key advantage of MFO on other algorithms is its ability to tackle several tough issues involving confined and unknown search spaces such as optical network unit placement [14], automatic generation control problem [15], image segmentation [16], feature selection [17], medical diagnoses [18], and smart grid system [19].
As a new population-based optimization method, MFO’s performance still needs to be improved and studied in some dimensions, including convergence speed and global search capabilities. Various academics have come up with a variety of ways to fix the MFO algorithm’s flaws and a few of these are presented here. In order to tackle the shortcomings of the MFO method, Hongwei et al. [20] presented a new form of the algorithm called chaos-enhanced MFO, which incorporates a chaotic map. Yueting et al. [21] proposed a series of new MFO algorithm variants by integrating MFO with Gaussian, Cauchy, and Levy mutations to reduce the disadvantages of the MFO and expand the search capability of MFO. To achieve a more stable balance between diversity and intensification in the MFO algorithm by embedding Gaussian mutation and chaotic local search, Xu et al. [22] developed CLSGMFO. Three additional adjustments were introduced to the MFO and suggested E-MFO by Kaur et al. [23] to keep a favorable balance between diversification and intensification and boost exploration and exploitation, respectively. For the prediction of software errors, Tumar et al. [24] implemented a modified MFO method and presented an extended binary moth-flame optimization algorithm (EBMFO). To strike a compromise between global and local search capabilities, Wei Gu and Gan Xiang [25] suggested a new modified MFO algorithm termed as a “multi operator MFO algorithm” (MOMFO). An updated version of the MFO algorithm was created by Ma and colleagues [26] to alleviate the MFO’s shortcomings, including delayed and local minimum convergence. A new version of the MFO, namely EMFO, based on the mutualism phase of symbiotic organism search, has been proposed by Sahoo et al. [27]. Few recent upgraded versions of MFO algorithms are discussed in [28–34].
Researchers have also developed more efficient algorithms in addition to the ones listed above. For example, Chakraborty et al. [35] introduced WOAmM, where the authors embedded the modified mutualism phase in WOA to alleviate inherent drawbacks of WOA. Nama et al. [36] proposed the hybrid SOS (HSOS) by integrating Simple Quadratic Interpolation (SQI) with SOS to enhance the robustness of the process. An effective hybrid method called m-MBOA has been developed by Sharma and Saha [37]. Because of this, BOA’s overall performance was enhanced by using mutualism in the exploring part. Chakraborty et al. [38] introduced an efficient hybrid method called HSWOA by hybridizing the HGS algorithm into the WOA algorithm and applied it to solve different engineering design problems. Sharma et al. [39] introduced a different type of modification in BOA named mLBOA in which Lagrange interpolation and SQI are used in exploration and exploitation phases, respectively, to improve the original BOA algorithm. In the present study, a modified MFO is formulated, namely Ft-MFO with the help of the Fibonacci technique. The major steps involved in this work are as follows:
- Firstly, a non-linear function is embedded into the classical MFO algorithm to maintain exploration and exploitation capability of the suggested Ft-MFO.
- Secondly, we merged the concept of Fibonacci search method in MFO to boost the solution quality of the proposed Ft-MFO.
- The efficiency of the new Ft-MFO is examined with six popular stochastic optimization algorithms on an IEEE CEC 2019 test suite and two constrained engineering problems.
- A Friedman rank test was carried out in order to investigate the performance of the newly suggested Ft-MFO algorithm.
The rest of this article is structured as follows. Section 18.2 provides an overview of the MFO algorithm. Section 18.3 shows the suggested Ft-MFO algorithm. Section 18.4 presents the simulation outcomes and performance metrics. Statistical tests and a convergence analysis are discussed in in Section 18.5, as well as real life problems. Finally, conclusions with future enhancements are discussed in Section 18.6.
18.2 Classical MFO Algorithm
This section presents the origin of the MFO algorithm and its working process with the mathematical formulation presented below.
Moths are members of the Arthropoda family. Moth navigation techniques are one-of-a-kind, which draws researchers’ attention. In the subsections that follow, the MFO algorithm is represented mathematically. The positions of all moths are represented using a vector of choice variables. Take a peek at the moth matrices below.
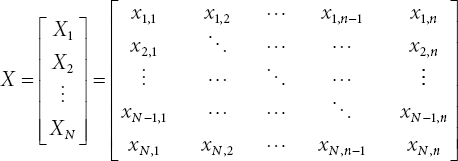
where ![]()
N is the number of moths in the original population, while n denotes variable numbers. The flame matrix (FMx) is the second crucial factor of the MFO algorithm. Mathematically, it can be represented as follows:

Moths move spirally when they are nearer to the flame, therefore the author used a logarithmic spiral function which is as follows:

where ![]() represents the distance of the moth at ith place and its specific flame (Fmi) and t can be any random number between −1 and 1. Here, b is a fixed constant used to recognize the spiral flight shape. A moth moves like a helix towards the flame with a one-dimensional approach and a discrete value of t and represented as follows:
represents the distance of the moth at ith place and its specific flame (Fmi) and t can be any random number between −1 and 1. Here, b is a fixed constant used to recognize the spiral flight shape. A moth moves like a helix towards the flame with a one-dimensional approach and a discrete value of t and represented as follows:
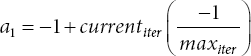
where maxiter and a1 indicate the maximum iterations and the constant of convergence, respectively, which decreases linearly from (−1) to (−2). In every iteration, flame positions for the current and last iterations are collected and arranged as per the fitness value for the global and local search. The number of flames (N.FM) that have been lowered over the iteration can be calculated using the formula below.
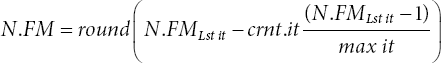
18.3 Proposed Method
The main characteristics of generalized optimization algorithms include exploration and exploitation. Exploration involves searching the entire search region. However, exploitation is characterized as examining limited areas within a large search field. These effects contribute to the algorithm’s ability to prevent local minima stagnation (as a result of exploitation) and to promote convergence and solution variety (from exploration). The equilibrium between these two occurrences is also vital. Any algorithm that achieves these three criteria is deemed as a state-of-the-art algorithm.
In MFO, the spiral motion of moths around the flame provides exploration and exploitation. It is easier to understand exploration and exploitation when the exponent factor ‘t’ is used to explain it. Iteratively, in traditional Ft-MFO, the parameter t is taken from the linearly decreasing range of (−1) to 2, but in our new approach we have introduced a non-linear decreasing range of (−1) to 2, which helps maintain an equilibrium of global and local search by first exploring the search space and then gradually shrinking and exploiting the region found. The following is a mathematical formula for the parameter ‘r.’
where k is a constant and its value is 0.55, which was suitably chosen so that it helps in both global and local searches and is represented in Figure 18.1.
Fibonacci Search Method (FSM)
The FSM is a mathematical process that shifts and narrows down the search range by using Fibonacci numbers to obtain the extreme value of unimodal functions. The optimal point is always contained within the range being narrowed. Shifting can take place in both directions. The values of that function at two experiment points determine the changing direction. The Fibonacci numbers, which are defined as follows, are the foundation of the FSM.
Fib = [F1, F2, F3, ... .., Fn], where, Fi ∀ i = 1,2,..n are Fibonacci numbers and generated by the following equation:

Figure 18.1 Non-linear adaption curve.
Let t1 and t2 be two experimental numbers of any finite length of interval with upper and lower limits as UL and LL, respectively. Calculate two initial points:
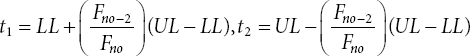
The range is moved to the right because the function’s value at t2 is greater than that at t1 and to the left if t1 is greater than that at t2. The new value of t3 and t4 are generated using the Fibonacci search formula as t3 = t1 and t4 = t2. If two functional values are unequal, then only one (t3 or t4) will be considered as a new experimental point, whereas the other will be the same as either of t1 and t2 depending on the contracting direction. In the case of two equal function values, then both t3 and t3 form new experimental points. Due to the high computational efficiency of FSM, the author of [40] used a modified Fibonacci search method for the partially shaded solar PV array. Recently, Yazici et al. [41] applied a modified Fibonacci search method for conversion systems of wind energy. We embedded the concept of the Fibonacci search method after the position update phase of MFO. The pseudocode of the projected Ft-MFO method is presented below as Algorithm 18.1.

18.4 Results and Discussions on IEEE CEC 2019 Benchmark Problems
It should be noted that the code for the proposed Ft-MFO algorithm has also been written in the MATLAB environment and run on a 1.80 GHz i5 8th generation computer with 8.00GB of RAM and MATLAB R2015a. In this paper, the proposed Ft-MFO has been applied on IEEE CEC 2019 test problems and the performance results are compared with a wide variety of state-of-the-art methods. The selected parameters of all population-based optimization algorithms involve the maximum iteration and number of populations as 1000 and 30, respectively. To determine the best set of parameters for Ft-MFO and all other algorithms, 30 trials are performed for each possible set of parameters. The studied cases are presented below.
The CEC 2019 benchmark function has stored more complex type functions than other CEC test suits. The author [42] developed some complex single objective optimization problems, namely, “The 100-digit Challenge”. There is a total of ten number functions that are multimodal and inseparable in nature. The first three functions (F1-F3) of CEC 2019 have different search ranges and different dimensions but the other seven functions (F4-F10) have the same search range with the same dimensions. The optimal value of all ten complex functions (F1-F10) is set to one.
Table 18.1 shows the performance results of 10 (ten) IEEE CEEC’2019 test suites using Ft-MFO and six basic current state-of-the-art optimization techniques, including MFO, DE, SOS, JAYA, BOA, and WOA. Table 18.2 shows how many times the efficiency of Ft-MFO is higher, similar to, and worse than that of other methods. In 8, 7, 8, 9, 7, and 8 benchmark functions, respectively, Ft-MFO outperforms MFO, DE, SOS, JAYA, BOA, and WOA; comparable results are seen in 2, 0, 0, 0, 2, and 0 benchmark functions, while poorer results are shown in 0, 3, 2, 1, 1, and 2 benchmark functions.
The Friedman Test, introduced by Milton Friedman [43], is a non-parametric statistical test. It is used to spot treatment variations across several test runs. The Friedman rank test has been employed in this study to equate the mean results of the algorithms for each benchmark issue. Table 18.3 shows that Ft-MFO has the lowest rank which is highlighted in bold, implying that its performance is superior to other algorithms. The convergence performance of Ft-MFO with other algorithms is shown in Figure 18.2, which is very competitive with respect to other methods.
Table 18.1 Simulation results of Ft-MFO and other algorithms on CEC’2019 suite.
| Algorithm | Fl | F2 | F3 | F4 | F5 | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| AVG | STD | AVG | STD | AVG | STD | AVG | STD | AVG | STD | |
| Ft-MFO | 1 | 0 | 5 | 0 | 8.40 | 1.59 | 3.34e+01 | 3.39e+01 | 1.64 | 1.68 |
| MFO | 1 | 0 | 5 | 0 | 9.62 | 9.60e-01 | 1.05e+02 | 1.56e+01 | 1.00e+02 | 2.59e+01 |
| DE | 1.82E+06 | 8.25E+05 | 1.93e+03 | 3.40e+02 | 4.58 | 6.11e-01 | 8.54 | 1.99 | 1.77 | 2.64e-02 |
| SOS | 4.75E+03 | 6.88E+03 | 2.65e+02 | 1.96e+02 | 4.61 | 9.78e-01 | 2.08e+72 | 3.42e+72 | 1.19e+73 | 4.40e+73 |
| JAYA | 6.53E+06 | 2.83e+06 | 4.68e+03 | 7.78e+02 | 8.09 | 7.57e-01 | 4.10e+01 | 4.90 | 2.60 | 1.67e-01 |
| BOA | 1 | 0 | 5 | 0 | 6.79 | 1.15 | 1.26e+02 | 2.15e+01 | 1.09e+02 | 2.33e+01 |
| WOA | 1.45E+08 | 1.17E+08 | 1.10E+04 | 3.36E+03 | 8.16 | 1.60 | 6.62E+01 | 2.40E+01 | 3.83 | 1.43 |
| Algorithm | F6 | F7 | F8 | F9 | F10 | |||||
| AVG | STD | AVG | STD | AVG | STD | AVG | STD | AVG | STD | |
| Ft-MFO | 3.07 | 1.21 | 8.22e+02 | 2.23e+02 | 4.25 | 2.41e-01 | 1.26 | 9.43e-02 | 2.15e+01 | 1.75e-01 |
| MFO | 1.21e+01 | 1.09 | 2.29e+03 | 2.51e+02 | 5.13 | 1.79e-01 | 3.86 | 6.23e-01 | 2.16e+01 | 1.43e-01 |
| DE | 1.11 | 1.48e-01 | 1.07e+03 | 1.24e+02 | 4.48 | 2.71e-01 | 1.29 | 4.20e-02 | 2.25e+01 | 2.52 |
| SOS | 2.15 | 2.22e-01 | 4.55e+71 | 4.09e+71 | 5.50 | 0 | 1.59e+71 | 2.34e+71 | 2.18e+01 | 8.74e-04 |
| JAYA | 5.90 | 9.23e-01 | 1.51e+03 | 2.09e+02 | 4.28 | 2.08e-01 | 1.56 | l.lle-01 | 2.16e+01 | 1.27e-01 |
| BOA | 1.36e+01 | 1.15 | 2.07e+03 | 2.89e+02 | 5.12 | 2.83e-01 | 4.14 | 5.51e-01 | 2.16e+01 | 1.85e-01 |
| WOA | 9.94 | 1.84 | 1.49E+03 | 2.85E+02 | 4.73 | 3.09E-01 | 1.48 | 1.69E-01 | 21.46 | 1.12E-01 |
Table 18.2 Experimental results of Ft-MFO with other algorithms on IEEE CEC’2019 test suite.
| MFO | DE | SOS | JAYA | BOA | WOA | |
|---|---|---|---|---|---|---|
| Superior to | 8 | 7 | 8 | 9 | 7 | 8 |
| Similar to | 2 | 0 | 0 | 0 | 2 | 0 |
| Inferior to | 0 | 3 | 2 | 1 | 1 | 2 |
Table 18.3 Friedman rank test.
| Algorithm | Mean rank | Rank |
|---|---|---|
| Ft-MFO | 3.40 | 1 |
| SOS | 3.76 | 2 |
| BOA | 4.08 | 3 |
| MFO | 4.66 | 4 |
| DE | 4.69 | 5 |
| WOA | 4.67 | 6 |
| JAYA | 4.79 | 7 |
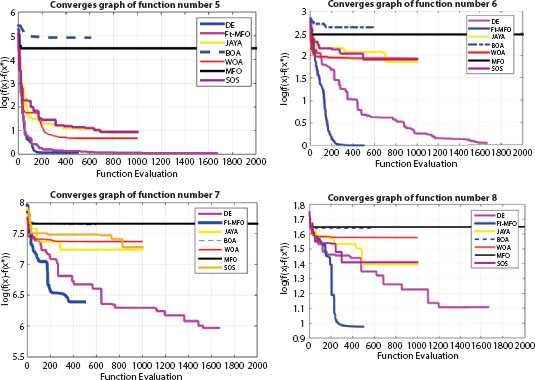
Figure 18.2 Convergence graph of Ft-MFO with other competative algorithms.
18.5 Real-Life Applications
Optimal gas production capacity and three-bar truss issues are utilized as real-world problems to show how well the proposed Ft-MFO algorithm works on real-life problems.
18.5.1 Optimal Gas Production Capacity Problem
The above problem is an unconstrained problem and details with mathematical representation are elaborated in [44].
The simulation results of the above problem are presented in Table 18.4. In this table, the results of DE, GSA, and DE-GSA are taken from [45]. From Table 18.4, we can conclude that the performance of the proposed Ft-MFO method is shown to be superior to that of other methods.
18.5.2 Three-Bar Truss Design (TSD) Problem
The challenge of designing a three-bar truss is one of structural optimization in civil engineering. Complex limited search space makes this challenge useful [46]. Two design criteria, buckling stress and deflection, have been modified in order to produce the lowest possible weight. The multiple components of the three-bar truss design issue are depicted in Figure 18.3.
Our new Ft-MFO algorithm is used to solve the TSD problem, which is then compared to the CS, DEDS, PSO-DE, Tsa, and MBA algorithms taken from the literature [12]. The comparative findings, as well as optimal weights and optimal variables, are provided in Table 18.5. Our suggested Ft-MFO technique outperforms the other three algorithms, as shown in Table 18.5.
Table 18.4 Simulation results for optimal gas production problem.
| Item | DE | MFO | GSA | DE-GSA | Ft-MFO |
|---|---|---|---|---|---|
| x1 | 17.5 | 17.5 | 17.5 | 17.5 | 17.5 |
| x2 | 600 | 600 | 600 | 600 | 600 |
| f(x) | 169.844 | 71.4495 | 169.844 | 169.844 | 71.4459 |
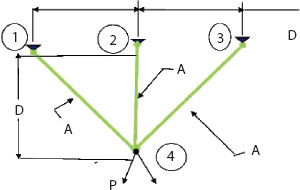
Figure 18.3 Three-bar truss design problem.
Table 18.5 Simulation results for three-bar truss problem.
| Algorithm | Optimal variables | Optimal weight | |
|---|---|---|---|
| x1 | x2 | ||
| Ft-MFO | 0.408966 | 0.288146 | 174.2762166 |
| MFO | 0.788244770931922 | 0.788244770931922 | 263.895979682 |
| CS | 0.78867 | 0.40902 | 263.9716 |
| DEDS | 0.78867513 | 0.40824828 | 263.8958434 |
| PSO-DE | 0.7886751 | 0.4082482 | 263.8958433 |
| Tsa | 0.788 | 0.408 | 263.68 |
| MBA | 0.7885650 | 0.4085597 | 263.8958522 |
18.6 Conclusion with Future Studies
This paper presents an upgraded variety of the classic MFO algorithm, namely an amended MFO (Ft-MFO) which uses a Fibonacci search concept and a non-linear adaption formula to improve the MFO algorithm and make a good tradeoff between diversification and intensification. To evaluate the performance of Ft-MFO, IEEE CEC 2019 benchmark functions have been considered for experimentations and compared with the basic MFO, DE, JAYA, BOA, SOS, and WOA. The Friedman Test is used to measure the effectiveness of the suggested Ft-MFO algorithm. It has also been used to solve two engineering issues, providing a better result than previous algorithms to validate the proposed Ft-MFO. According to simulation results, using the global best solution in the optimization process quickly brought the proposed method into focus. To avoid local optima traps and premature convergence, the proposed technique is helpful.
In the future we can extend it to multi-objective optimization, apply it to solve higher constraint optimization problems like car-side crash problems, robot gripper problems, welded beam design problems, etc. We can generate an efficient metaheuristic algorithm by hybridizing our suggested approach, Ft-MFO, with any other meta-heuristic algorithm.
References
- 1. Abbassi, R., Abbassi, A., Heidari, A. A., & Mirjalili, S. (2019). An efficient salp swarm-inspired algorithm for parameters identification of photovoltaic cell models. Energy Conversion and Management, 179, 362–372.
- 2. Faris, H., Ala’M, A.-Z., Heidari, A. A., Aljarah, I., Mafarja, M., Hassonah, M. A., & Fujita, H. (2019). An intelligent system for spam detection and identification of the most relevant features based on evolutionary random weight networks. Information Fusion, 48, 67–83.
- 3. McCarthy, J. F. (1989). Block-conjugate-gradient method. Physical Review D, 40(6), 2149.
- 4. Wu, G., Pedrycz, W., Suganthan, P. N., & Mallipeddi, R. (2015). A variable reduction strategy for evolutionary algorithms handling equality constraints. Applied Soft Computing, 37, 774–786.
- 5. Holland, J. H. (1992). Genetic algorithms. Scientific American, 267(1), 66–73.
- 6. Kennedy, J., Eberhart, R. Particle swarm optimization. In: Proceedings of ICNN’95—international conference on neural networks, Perth, Australia, 1995, 1942–1948.
- 7. Storn, R., & Price, K. (1997). Differential evolution–a simple and efficient heuristic for global optimization over continuous spaces. Journal of Global Optimization, 11(4), 341–359.
- 8. Dhiman, G., & Kumar, V. (2017). Spotted hyena optimizer: A novel bio-inspired based metaheuristic technique for engineering applications. Advances in Engineering Software, 114, 48–70.
- 9. Arora, S., & Singh, S. (2015). Butterfly algorithm with levy flights for global optimization. 2015 International Conference on Signal Processing, Computing and Control (ISPCC), 220–224.
- 10. Mirjalili, S., & Lewis, A. (2016). The whale optimization algorithm. Advances in Engineering Software, 95, 51–67.
- 11. Mirjalili, S. (2016). SCA: A sine cosine algorithm for solving optimization problems. Knowledge-Based Systems, 96, 120–133.
- 12. Mirjalili, S. (2015). Moth-flame optimization algorithm: A novel natureinspired heuristic paradigm. Knowledge-Based Systems, 89, 228–249.
- 13. Mirjalili, S., Gandomi, A. H., Mirjalili, S. Z., Saremi, S., Faris, H., & Mirjalili, S. M. (2017). Salp Swarm Algorithm: A bio-inspired optimizer for engineering design problems. Advances in Engineering Software, 114, 163–191.
- 14. Singh, P., & Prakash, S. (2019). Optical network unit placement in Fiber-Wireless (FiWi) access network by Whale Optimization Algorithm. Optical Fiber Technology, 52, 101965.
- 15. Mohanty, B. (2019). Performance analysis of moth flame optimization algorithm for AGC system. International Journal of Modelling and Simulation, 39(2), 73–87.
- 16. Khairuzzaman, A. K. M., & Chaudhury, S. (2020). Modified MothfFlame optimization algorithm-based multilevel minimum cross entropy thresholding for image segmentation: International Journal of Swarm Intelligence Research, 11(4), 123–139.
- 17. Gupta, D., Ahlawat, A. K., Sharma, A., & Rodrigues, J. J. P. C. (2020). Feature selection and evaluation for software usability model using modified moth-flame optimization. Computing, 102(6), 1503–1520.
- 18. Muduli, D., Dash, R., & Majhi, B. (2020). Automated breast cancer detection in digital mammograms: A moth flame optimization-based ELM approach. Biomedical Signal Processing and Control, 59, 101912.
- 19. Kadry, S., Rajinikanth, V., Raja, N. S. M., Hemanth, D. J., Hannon, N. M., & Raj, A. N. J. (2021). Evaluation of brain tumor using brain MRI with modified-moth-flame algorithm and Kapur’s thresholding: A study. Evolutionary Intelligence, 1–11.
- 20. Hongwei, L., Jianyong, L., Liang, C., Jingbo, B., Yangyang, S., & Kai, L. (2019). Chaos-enhanced moth-flame optimization algorithm for global optimization. Journal of Systems Engineering and Electronics, 30(6), 1144–1159.
- 21. Xu, Y., Chen, H., Luo, J., Zhang, Q., Jiao, S., & Zhang, X. (2019). Enhanced moth-flame optimizer with mutation strategy for global optimization. Information Sciences, 492, 181–203.
- 22. Xu, Y., Chen, H., Heidari, A. A., Luo, J., Zhang, Q., Zhao, X., & Li, C. (2019). An efficient chaotic mutative moth-flame-inspired optimizer for global optimization tasks. Expert Systems with Applications, 129, 135–155.
- 23. Kaur, K., Singh, U., & Salgotra, R. (2020). An enhanced moth flame optimization. Neural Computing and Applications, 32(7), 2315–2349.
- 24. Tumar, I., Hassouneh, Y., Turabieh, H., & Thaher, T. (2020). Enhanced binary moth flame optimization as a feature selection algorithm to predict software fault prediction. IEEE Access, 8, 8041–8055.
- 25. Gu, W., & Xiang, G. (2021). Improved moth flame optimization with multioperator for solving real-world optimization problems. 2021 IEEE 5th Advanced Information Technology, Electronic and Automation Control Conference (IAEAC), 5, 2459–2462.
- 26. Ma, L., Wang, C., Xie, N., Shi, M., Ye, Y., & Wang, L. (2021). Moth-flame optimization algorithm based on diversity and mutation strategy. Applied Intelligence.
- 27. Sahoo, S. K., Saha, A. K., Sharma, S., Mirjalili, S., & Chakraborty, S. (2022). An enhanced moth flame optimization with mutualism scheme for function optimization. Soft Computing, 26(6), 2855–2882.
- 28. Sahoo, S. K., & Saha, A. K. (2022). A hybrid moth flame optimization algorithm for global optimization. Journal of Bionic Engineering, 19(5), 1522–1543.
- 29. Sahoo, S. K., Saha, A. K., Nama, S., & Masdari, M. (2022). An improved moth flame optimization algorithm based on modified dynamic opposite learning strategy. Artificial Intelligence Review, 1–59.
- 30. Sahoo, S. K., Saha, A. K., Sharma, S., Mirjalili, S., & Chakraborty, S. (2022). An enhanced moth flame optimization with mutualism scheme for function optimization. Soft Computing, 26(6), 2855–2882.
- 31. Sahoo, S.K., Saha, A.K., Ezugwu, A.E. et al. Moth flame optimization: theory, modifications, hybridizations, and applications. Arch Computat Methods Eng (2022). https://doi.org/10.1007/s11831-022-09801-z.
- 32. Chakraborty, S., Saha, A. K., Sharma, S., Sahoo, S. K., & Pal, G. (2022). Comparative performance analysis of differential evolution variants on engineering design problems. Journal of Bionic Engineering, 19(4), 1140–1160. https://doi.org/10.1007/s42235-022-00190-4.
- 33 Sahoo, S. K., Sharma, S., & Saha, A. K. (2023). A Novel variant of moth flame optimizer for higher dimensional optimization problems, 1–27.
- 34. Sahoo, S. K., & Saha, A. K. (2022, August). A modernized moth flame optimization algorithm for higher dimensional problems. In ICSET: International Conference on Sustainable Engineering and Technology, (Vol. 1, No. 1, pp. 9–20).
- 35. Chakraborty, S., Kumar Saha, A., Sharma, S., Mirjalili, S., & Chakraborty, R. (2021). A novel enhanced whale optimization algorithm for global optimization. Computers & Industrial Engineering, 153, 107086.
- 36. Nama, S., Saha, A. K., & Ghosh, S. (2017). A hybrid symbiosis organisms search algorithm and its application to real world problems. Memetic Computing, 9(3), 261–280.
- 37. Sharma, S., & Saha, A. K. (2020). m-MBOA: A novel butterfly optimization algorithm enhanced with mutualism scheme. Soft Computing, 24(7), 4809–4827.
- 38. Chakraborty, S., Saha, A. K., Chakraborty, R., Saha, M., & Nama, S. (2022). HSWOA: An ensemble of hunger games search and whale optimization algorithm for global optimization. International Journal of Intelligent Systems, 37(1), 52–104.
- 39. Sharma, S., Chakraborty, S., Saha, A. K., Nama, S., & Sahoo, S. K. (2022). mLBOA: A Modified Butterfly Optimization Algorithm with Lagrange Interpolation for Global Optimization. Journal of Bionic Engineering.
- 40. Ramaprabha, R. (2012). Maximum power point tracking of partially shaded solar PV system using modified Fibonacci search method with fuzzy controller. 12.
- 41. Yazıcı, İ., Yaylacı, E. K., Cevher, B., Yalçın, F., & Yüzkollar, C. (2021). A new MPPT method based on a modified Fibonacci search algorithm for wind energy conversion systems. Journal of Renewable and Sustainable Energy, 13(1), 013304.
- 42. Price, K. V., Awad, N. H., Ali, M. Z., & Suganthan, P. N. (2018). Problem definitions and evaluation criteria for the 100-digit challenge special session and competition on single objective numerical optimization. In Technical Report. Nanyang Technological University.
- 43. Milton F. (1937). The use of ranks to avoid the assumption of normality implicit in the analysis of variance. Journal of the American Statistical Association. 32: 675–701.
- 44. Nama, S. (2021). A modification of I-SOS: performance analysis to large scale functions. Applied Intelligence, 51(11), 7881–7902.
- 45. Muangkote, N., Sunat, K., & Chiewchanwattana, S. (2016). Multilevel thresholding for satellite image segmentation with moth-flame based optimization. 2016 13th International Joint Conference on Computer Science and Software Engineering (JCSSE), 1–6.
- 46. Gandomi A.H., Yang X.S., Alavi A.H. (2011). Mixed variable structural optimization using firefly algorithm. Computers & Structures 89:2325-36.
Note
- ⋆ Corresponding author: [email protected]
