26
Estimating Error of Signals by Product Means  (C, 2) of the Fourier Series in a W(Lr, ξ(t)) (r ≥ 1) Class
(C, 2) of the Fourier Series in a W(Lr, ξ(t)) (r ≥ 1) Class
Pankaj Tiwari⋆ and Aradhana Dutt Jauhari†
Division of Mathematics, Department of Basic Sciences, Galgotias University, Greater Noida, G. B. Nagar, U.P., India
Abstract
The goal of this paper is to approach a new result on the degree of Fourier series approximation of a function g ∈ W(Lr, ξ(t))(r ≥ 1) class by ![]() product summability. Signals are handled as one-variable functions, while images are represented as two-variable functions. The concept’s research is directly tied to the rapidly developing field of information technology. The approximation theory is a trigonometric polynomial approximation. Many academics have researched in similar lines, but our research also proves some fresh findings.
product summability. Signals are handled as one-variable functions, while images are represented as two-variable functions. The concept’s research is directly tied to the rapidly developing field of information technology. The approximation theory is a trigonometric polynomial approximation. Many academics have researched in similar lines, but our research also proves some fresh findings.
Keywords: Degree of approximation, ![]() -means, weighted generalized lipschitz class, Fourier series, Lebesgue integral
-means, weighted generalized lipschitz class, Fourier series, Lebesgue integral
26.1 Introduction
Let L = L(0, 2π) denote the space of 2π-periodic and Lebesgue integrable functions on the (0, 2π) Fourier series at point x:
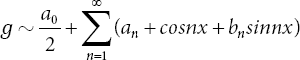
Let ∑an be an nth partial sum sequence {sn} in an infinite series [9].
26.1.1 Definition 1
The transformation from sequence to sequence [5]:
The ![]() mean of the sequence {sn} generalized by the series is defined by the sequence
mean of the sequence {sn} generalized by the series is defined by the sequence ![]() .
.
26.1.2 Definition 2
Riesz means can also be expressed as:
where Rn = p0 q0 + p1q1 + ⋯ + pnqn(≠ 0), p(−1) = q(−1) = R(−1) = 0.
The series ![]() is
is ![]() and is then summable to s.
and is then summable to s.
We have the following regularity conditions for Riesz summability [10]:
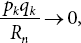 , For each integer k ≥ 0, as n → ∞.
, For each integer k ≥ 0, as n → ∞.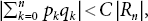 where C can be any positive integer irrespective of n.
where C can be any positive integer irrespective of n.
26.1.3 Definition 3
The (C,2) summability nth partial sum of the (C,2) transform is given [3]-.
By using the (C,2) method, the infinite series ![]() can be summable to the definite as the number.
can be summable to the definite as the number.
26.1.4 Definition 4
![]() of {sn} is a composite transformation over (C,2) as
of {sn} is a composite transformation over (C,2) as

If ![]() is n → ∞, then ∑an can be summable to s using
is n → ∞, then ∑an can be summable to s using ![]() means.
means.
26.1.5 Remark 1
If qn = 1, then in (26.2) the ![]() , summability method reduces with
, summability method reduces with ![]() summability and it reduces to
summability and it reduces to ![]() , summability.
, summability.
Also, the degree to which of the function g: R → R is approximated by a trigonometric polynomial tn of degree n:
A function f(x) ∈ Lipα, if
and g(x) ∈ Lip(α, r), for 0 ≤ x ≤ 2π, if

This is also applicable to any function that increases in a positive way ξ(t), g(x) ∈ Lip(ξ(t), r), if
This is also applicable to any function that increases in a positive way ξ(t), an integer r ≥ 1, f ∈ W(Lr, ξ(t))
We will use the notations below as a guide:

Then, the weighted W(Lr, ξ(t)) class is a subset of the Lipα, Lip(α, r), and Lip(ξ(t), r) classes. As a result, the following additions have been made:
for all 0< α ≤ 1 and r≥1.
26.2 Known Result
In 2011, Nigam [1] proved a theorem on (C,1)(E,q) means of the Fourier series. Proceeding the work in 2014, Mishra et al. [4], the product (E,s) (N,pn, qn) - summability mean of the Fourier series showed a theorem on the degree of approximation. Pradhan [5] proposed the following theorem in 2016.
26.2.1 Theorem 1
If f ∈ W(Lr, ξ(t)) class is a 2π-periodic function that is integrable in the Lebesgue sense in [0,2π], then the degree of approximation is given by

where ![]() is the
is the ![]() (E,s) transform of {sn}, provided ξ(t) has the following requirements:
(E,s) transform of {sn}, provided ξ(t) has the following requirements: ![]() is a decreasing sequence,
is a decreasing sequence,

26.3 Main Theorem
Various mathematicians including Nigam [2], Deger [6], and Mishra et al. [7, 8] studied the degree of approximation using various summability approaches. By using the Riesz-Cesaro product summability approach, we obtain a novel result on the degree of approximation of function g ∈ W(Lr, ξ(t)) class.
The following theorem is established.
26.3.1 Theorem 2
If g ∈ W(Lr, ξ(t)) with ![]() , the degree of approximation by Riesz-Cesaro product mean of the Fourier series satisfies for n = 0,1,2…
, the degree of approximation by Riesz-Cesaro product mean of the Fourier series satisfies for n = 0,1,2…
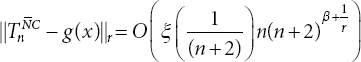
where ![]() is the
is the ![]() transform of sn, supposing that function ξ(t) satisfies the required criteria,
transform of sn, supposing that function ξ(t) satisfies the required criteria,
![]() is a function that does not increase and
is a function that does not increase and
where δ is an arbitrarily defined s.t. qs(β − δ) – 1 > 0
r−1 + s−1 = 1, r ≥ 1 and (26.12) and (26.13) uniformly hold in x.
26.4 Some Auxiliary Results
Uniformly holding the following lemmas is necessary to prove the above theorem.
26.4.1 Lemma-1
For
we get Pn(t) = O(n + 2)

26.4.2 Lemma-2
For (n + 2)−1 < t < π
we get ![]()

Using Jordan’s Lemma ![]() and sinkt ≤, we have
and sinkt ≤, we have
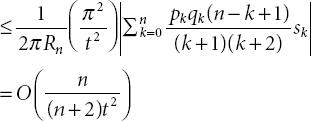
26.5 Theorem’s Proof
Using Riemann-Lebesgue theorem, we have

The Riesz Cesaro transform of the sequence is given by
where ![]()
Applying Minikowski’s inequality, since

and the fact that
![]() and Lemma 1, we have
and Lemma 1, we have
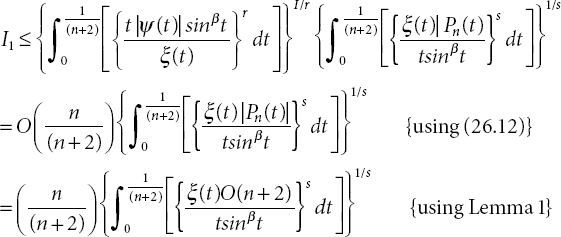
Using the second mean value theorem for integrals, ξ(t) is a decreasing function and we get
Now,
Using Hölder’s inequality as a starting point, ![]()

we put t =1/x, dt = -(1/x2)dx

Because ξ(t) > 0 and  are both rising functions, the second mean value theorem is used and
are both rising functions, the second mean value theorem is used and
from (26.14) and (26.15), (26.16) becomes
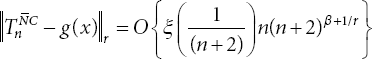
26.6 Applications
From our main theorem, we can derive the following corollaries.
26.6.1 Cor. 1
If ξ(t) = tα, then weighted class W(Lr, ξ(t)), 1 ≤ r < ∞ reduces to the group of class Lip(α, r) and then a function f is a degree of approximation belonging to the class Lip(α, r), r−1 ≤ α ≤ 1, given by
Proof: Setting produces, the result is β = 0 in (26.5).
26.6.2 Cor. 2
For r → ∞ in Cor. 1 for the class function, g ∈ Lip(α, r) reduces to the class Lip α and a function g belonging to the class Lipα, 0 < α < 1 whose degree of the approximation is given by
26.7 Conclusion
The previous finding on function degree of approximation demonstrated that the result is frequently true in nature and can be simplified to a few special cases. As a result, the current research can be used for a series of issues in the fields of analysis, technology, and engineering. Figure 26.1 shows some unique behaviour in the Fourier series approximations [11].
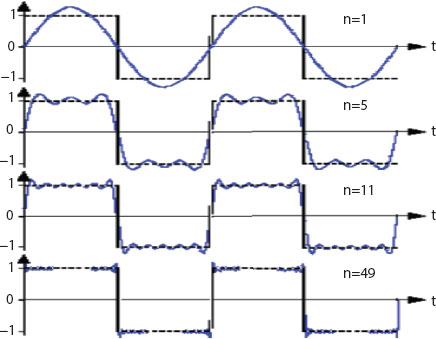
Figure 26.1 Approximations of such Fourier Series to sq (t). Each plot indicates the number of terms in the Fourier sum and the square wave is displayed as a dashed line over two periods.
Acknowledgement
The sincere gratitude goes to the anonymous referees for their careful reading, remarks, and valuable comments, as well as many other useful suggestions for improved presentation. The author wishes to express his appreciation to the members of the editorial board.
References
- 1. H. K. Nigam: “Degree of approximation of a function belonging to weighted (Lip (ξ(t), r) class by (C,1) (E,q) means”, Tamkang Journal of Mathematics, 42, 31-37 (2011).
- 2. H. K. Nigam: “On Approximation of functions by product operators”, Survey in Mathematics and its Applications ISSN 1842-6298(Electronic), 1843-7265(print) Volume 8 (2013), 125-136.
- 3. K. Sharma. and S.S. Malik: “Degree of Approximation by Product means of the Fourier Series in a
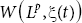 (r > −1 by (E,1)(C,2) product summability Transform”, International Journal of Mathematical Trends and Technology (IJMTT), Volume-8 Number-2,ISSN 2231-5373,2014, 10.14445/22315373/IJMTT-V8P518.
(r > −1 by (E,1)(C,2) product summability Transform”, International Journal of Mathematical Trends and Technology (IJMTT), Volume-8 Number-2,ISSN 2231-5373,2014, 10.14445/22315373/IJMTT-V8P518. - 4. M. Mishra et al.: “Approximation of Fourier series of a function of Lipschitz class by product means” Journal of advances in Mathematics, 9 2475-2484 (2014).
- 5. T. Pradhan et al.: “Approximation of signals belonging to generalised Lipschitz class using
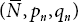 -summability mean of Fourier series”, Cogent Mathematics (2016),3: 1250343.http://dx.doi.org/10.1080/23311835.2016.1250343.
-summability mean of Fourier series”, Cogent Mathematics (2016),3: 1250343.http://dx.doi.org/10.1080/23311835.2016.1250343. - 6. U. De
 er: “On Approximation to functions in the
er: “On Approximation to functions in the 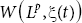 class by a new matrix mean”, Novi Sad J. Math, Vol.46 No.1, 2016, 1-14.
class by a new matrix mean”, Novi Sad J. Math, Vol.46 No.1, 2016, 1-14. - 7. V. N. Mishra et al.: “Approximation of Signals by Product Summability Transform”, Asian Journal of Mathematics and Statistics 6(1): 12-22, 2013, ISSN 1994-5418/ DOI: 10.3923/AJMS.2013,12.22.
- 8. V. N. Mishra, K. Khatri, L. N. Mishra: “Product Summability Transform of Conjugate series of Fourier series”, Hindawi Publishing Corporation, International Journal of Mathematics and Mathematical Sciences, Volume 2012, Article 1D 298923, 13 pg doi: 10.1155/2012/298923.
- 9. A. Zygmund: “Trigonometric Series”, second ed., Cambridge University Press, Cambridge, 1959.
- 10. G. H. Hardy: Divergent Series Oxford University Press 1st Ed. 1949.
- 11. https://eng.libretexts.org/Bookshelves/Electrical_Engineering.
Notes
- ⋆ Corresponding author: [email protected]
- †Corresponding author: [email protected]