24
An Approach to Ranking of Single Valued Neutrosophic Fuzzy Numbers Based on (α, β, γ) Cut Sets
Sunayana Saikia
Department of Mathematics, Cotton University, Guwahati, Assam, India
Abstract
In most real-world applications, single-valued neutrosophic fuzzy numbers are employed to make judgments in a fuzzy environment. As a result, single-valued neutrosophic fuzzy number ranking is crucial. This paper proposes a novel approach for ranking single-valued neutrosophic fuzzy numbers. The approach was created by combining the α, β, and γ cuts of neutrosophic fuzzy numbers in a convex way. In addition, the proposed approach has been used to prove a number of theorems. This paper also offers a number of numerical examples.
Keywords: Single valued neutrosophic fuzzy numbers, α-cut set, β-cut set, γ-cut set, ranking of neutrosophic fuzzy numbers, convex combination
24.1 Introduction
Real-life phenomena cannot be classified by real numbers due to the existence of linguistic concepts. Fuzzy numbers can be used to rate such issues because fuzzy numbers may deal with verbal words that are ambiguous or vague. As a result, numerous ways for ranking fuzzy numbers have been presented at various times. In addition, the ordering of fuzzy numbers has been thoroughly examined. In the literature, there are several research articles that describe various strategies for sorting fuzzy numbers. In a nutshell, no universally accepted method for sorting fuzzy numbers exists. Existing methods have been demonstrated to give outcomes that are counter-intuitive at times. Furthermore, some of these strategies are non-discrimi-natory and counter intuitive. In 1965, Zadeh [33] “was the first to introduce the notion of fuzzy set theory”. Many academics have worked hard to come up with new and better techniques to rank the unclear numbers. Jain [18, 19] introduced the first unorthodox efforts to the condition of “ordering fuzzy quantities using maximizing set” in 1976. After that, “some ranking methods of fuzzy numbers examined and compared” by Bortolan and Degani [4] and Burnelli and Mezei [5]. In addition, Wang and Kerre [30, 31], Dubois and Prade [15], Chen [6], Choobineh and Li [9], Yu and Dat [32], Chen and Sanguansat [7], Chen et al. [8], Shureshjani and Darehmiraki [25], Chutia [10], Chutia and Chutia [11], Chutia and Gogoi [12], and so forth proposed some ranking methods and some properties of the ranking methods. In 1998, Smarandache [26–28] did the first pioneering work on neutrosophic fuzzy numbers. Ulucay et al. [29], Karaaslan [23], Deli [13], Jana and Pal [21], Jana et al. [20, 22], and others utilized the neutrosophic number for a variety of decision-making situations. Several studies have been conducted on the ordering of single-valued neutrosophic numbers. Peng et al. [24] established a single-valued neutrosophic number ranking system that was subsequently used to “multi-criteria decision making issues”. To rank the single-valued neutrosophic numbers, Deli and Subas [14], Biswas et al. [3], and Aal et al. [1] “presented values and ambiguities of truth membership, indeterminacy-membership, and falsity-membership functions”. Garai et al. [34] “devised a single-valued neutrosophic number ranking system based on possible mean, variance, and standard deviation, which they subsequently applied to multi-attribute group decision-making difficulties”. Garai et al. [16] “proposed a weighted possibility means-based ranking method for single-valued neutrosophic numbers”. Bhaumik et al. [2] “proposed a new ranking method for single-valued neutrosophic numbers established on the (α, β, γ)-cut set, which was then used to the solution of bi-matrix games”.
Because of their linguistic terms, ranking fuzzy numbers plays a distinguishing part in the decision-making process. In some decision-making scenarios, rating single-valued neutrosophic numbers is crucial. Single-valued neutrosophic numbers can be ranked using a variety of approaches. Furthermore, existing single-valued neutrosophic fuzzy number ranking algorithms are incorrect in several instances. As a result, new ways are required to overcome present methods’ limits and downsides. This study makes an effort at doing so. The suggested technique is based on a convex combination of single-valued neutrosophic numbers from the α, β, and γ cut sets.
In Section 24.2, some fundamental definitions and arithmetic of single valued neutrosophic fuzzy numbers are covered. The convex combination of α-cut, β-cut, and γ-cut sets of a single valued neutrosophic fuzzy number are proposed in Section 24.3 as a novel ranking technique for single valued neutrosophic fuzzy numbers. With the aid of the suggested ranking mechanism, we establish certain theorems in Section 24.4. Some numerical examples of the suggested technique are presented in Section 24.5. The proposed method’s conclusion and future studies has been presented in Section 24.6.
24.2 Definition and Representations
This section looked at several definitions and representations for the idea of single-valued neutrosophic fuzzy numbers.
Definition 24.2.1 ([11]). “Let A represent a set and X represent the universal set, with A ∈ X. The set of ordered pairs A = {(x, µA(x)): x ∈ X, µA,: X → [0, 1]} is then referred to as a fuzzy set and µA is the membership function”.
Definition 24.2.2 ([11]). “Let a fuzzy number A = (x, µA(x)) = (a, b, c, d; wA) and if the membership function µA(x) is represented as,

then the fuzzy number A is called a generalized trapezoidal fuzzy number (GTrFN)”.
Definition 24.2.3 ([11]). “An intuitionistic fuzzy set (IFS) A on ℝ is defined as A = ⟨x, µA(x), νA(x)⟩: x ∈ ℝ), where the function µA: ℝ → [0, 1] is known as the degree of membership and νA: ℝ → [0, 1] is known as the degree of non-membership of the element x ∈ ℝ, such that 0 ≤ µA(x) + νA(x) ≤ 1”.
Definition 24.2.4 ([11]). “Consider an intuitionistic fuzzy number (IFN) A = ⟨(a, b, c, d; wA), (p, q, r, s; uA)⟩, where c ≤ a, q ≤ b ≤ c ≤ r, d ≤ s are the parameters. The membership function and the non-membership function are defined as:

respectively, where wA is the maximum degree of membership and uA is the minimum degree of non-membership such that 0 ≤ wA ≤ 1, 0 ≤ uA ≤ 1 and 0 ≤ wA + uA ≤ 1”.
Definition 24.2.5 ([17]). “Assume that X is the universal set and that A is a set in X. The ordered pair set A = {⟨x, µA(x), νA(x), ρA(x)⟩: x ∈ X} is a single-valued neutrosophic set (SVNS), with µA(x) being the truth membership degree, defined as µA: X → [0, 1], νA(x) being the indeterminacy membership degree, defined as νA: X → [0, 1] and ρA(x) being the falsity membership degree is defined as ρA: X → [0, 1], of the element x to the set A, with the constraint 0 ≤ µA(x) + νA(x) + ρA(x) ≤ 3, ∀x ∈ X”.
Definition 24.2.6 ([17]). “A SVNS A = {⟨x, µA(x), νA(x), ρA(x)⟩∀x ∈ X} is said to be neutrosophic-normal if there exist at least three points a, b, c ∈ X where µA: a → {1}, νA: b → {1} and ρA: c → {1}”.
Definition 24.2.7 ([17]). “An (α, β, γ)-cut set of a SVNS A is a crisp subset over the set of real numbers ℝ which are defined as, A(α, β, γ) = {x,: µA(x) ≥ α, νA(x) ≤ β, ρA(x) ≤ γ}, with 0 ≤ α ≤ 1, 0 ≤ β ≤ 1 and 0 ≤ α + β + γ ≤ 3”.
Definition 24.2.8 ([17]). “A SVNS, A = {⟨x, µA(x), νA(x), ρA(x)⟩∀x ∈ X} is called neutrosophic-convex if:
- µA(λa + (1 − λ)b) ≥ min(µA(a), µA(b)),
- νA(λa + (1 − λ)b) ≤ max(νA(a), νA(b)),
- ρA(λa + (1 − λ)b) ≤ max(ρA(a), ρA(b)), for all a, b ∈ X and λ ∈ [0, 1]”.
Definition 24.2.9 ([17]). “A single-valued nutrosophic set {A = ⟨x, µA(x), νA(x), ρA(x)⟩∀x ∈ X} is said to be a single-valued neutrosophic number (SVNN) if,
- A is neutrosophic-normal,
- A is neutrosophic-convex,
- µA is upper semi-continuous, νA, and ρA are lower semi-continuous,
- Support (S(A)) of A is bounded, i.e., S(A) = {µA(x) > 0, νA < 1, ρA < 1, ∀x ∈ X}”.
Definition 24.2.10 ([17]). “A SVNS, A = {⟨x, µA(x), νA(x), ρA(x)⟩∀x ∈ X},= ⟨(a1, b1, c1), (i1, j1, k1), (p1, q1, r1)⟩ in the set of real numbers is said to be single-valued triangular neutrosophic number (SVTNN), such that p1 ≤ i1 ≤ a1 ≤ q1 ≤ j1 ≤ b1 ≤ c1 ≤ j1 ≤ r1 are the parameters. Then, the truth membership degree, the indeterminacy membership degree, and thee falsity membership degree of A can be defined as:”


Definition 24.2.11 ([2]). Cut Sets of SVTNN
“Let, a SVTNN A = {⟨µA(x), νA(x), ρA(x)⟩: x ∈ X} = ⟨(a1, b1, c1), (i1, j1, k1), (p1, q1, r1)⟩, where a1, b1, c1, i1, j1, k1, p1, q1, r1 ∈ R. Then, (α, β, γ)-cut sets of A are defined as:
- α-cut set: Aα = {x: µA(x) ≥ α} = [Lα(A), Rα(A)] = [a1 + α(i1 − a1), p1 − α(p1 − i1)],
- β-cut set: Aβ = {x: νA(x) ≤ β} = [Lβ(A), Rβ(A)] = [b1 + β(j1 − b1), b31 − β(q1 − j1)],
- γ-cut set: Aγ = {x: ρA(x) ≤ γ} = [Lγ(A), Rγ(A)] = [c1 + γ(k1 − c1), r1 − γ(r1 − k1)]”.
Definition 24.2.12 ([2]). Defined the Quantity Value
“Let A = {⟨µA(x), νA(x), ρA(x)⟩: x ∈ X} be a SVNN. Then,
- The value of a SVTNN “A” for the truth membership function is denoted by Vµ(A) and is defined as

where α ∈ [0, 1] and the weighted function f (α) = α satisfies the condition f (0) = 0 and f (1) = 1, such that
 .
. - The value of a SVTNN “A” for the indeterminacy membership function is denoted by Vν(A) and is defined as

where β ∈ [0, 1] and the weighted function g(β) = 1 − β satisfy the condition g(0) = 1 and g(1) = 0, such that
 .
. - The value of a SVTNN “A” for falsity membership function is denoted by Vρ(A) and is defined as
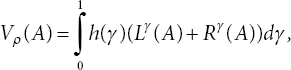
where γ ∈ [0, 1] and the weighted function h(γ) = 1 − γ satisfy the condition h(0) = 1 and h(1) = 0, such that
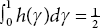 .
.
Definition 24.2.13 ([2]). Arithmetic
Let two SVTNNs as A = {⟨µA(x), νA(x), ρA(x)⟩: x ∈ X} = ⟨(a1, b1, c1), (i1, j1, k1), (p1, q1, r1)⟩ ∈ ℝ and B = {⟨µB(x), νB(x), ρB(x)⟩: x ∈ X} = ⟨(a2, b2, c2), (i2, j2, k2), (p2, q2, r2)⟩ ∈ ℝ, where µA and µB are truth memberships, νA and νB are indeterminacy memberships, and ρA and ρB are falsity memberships of A and B, respectively. Then,
- “A + B = ⟨(a1 + a2 − a1a2, b1 + b2 − b1b2, c1 + c2 − c1c2), (i1i2, j1j2, k1k2), (p1p2, p1q2, r1r2)⟩,
- A × B = ⟨(a1b1, a2b2, c1c2), (i1 + i2 − i1i2, j1 + j2 − j1j2, k1 + k2 − k1k2), (p1 + p2 − p1p2, q1 + q2 − q1q2, r1 + r2 − r1r2)⟩,
- κA = ⟨(1 − (1 − a1)κ, 1 − (1 − b1)κ, 1 − (1 − c1)κ),
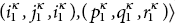 , where κ can be any real number,
, where κ can be any real number, - Aκ = ⟨((a1)κ, (b1)κ, (c1)κ), (1−(1−i1)κ, 1−(1−j1)κ, 1−(1−k1)κ), ((p1)κ, 1−(1−q1)κ, 1−(1−r1)κ)⟩, where κ can be any real number”.
24.3 Proposed Method
Here, a new ranking method for single-valued neutrosophic fuzzy numbers (SVNFNs) has been discussed. Consider a fuzzy number A ∈ X to be a SVTNN, such as A = ⟨x, µA(x), νA(x), ρA(x)⟩ = ⟨[Lα(A), Rα(A)], [Lβ(A), Rβ(A)], [Lγ(A), Rγ(A)]⟩, 0 ≤ α, β, γ ≤ 1, “where [Lα(A), Rα(A)] is α- cut set, [Lβ(A), Rβ(A)] is β- cut set and [Lγ(A), Rγ(A)] is γ-cut set for truth membership function, indeterminacy membership function, and falsity membership function” of the SVTNN A, respectively.
Then, the proposed ranking index at α, β, γ cuts is defined as

where λ1, λ2, λ3 ∈ [0, 1].
Thus, the ordering of the fuzzy numbers A, B ∈ X, based on the ranking index ![]() is defined as:
is defined as:
 (A) >
(A) >  (B), then A ≻ B;
(B), then A ≻ B; (A) <
(A) <  (B), then A ≺ B;
(B), then A ≺ B; (A) =
(A) =  (B), then A ~ B;
(B), then A ~ B;
where (0 ≤ λ1, λ2, λ3 ≤ 1).
24.4 Theorems
Some crucial and fundamental theorems are discussed here.
Theorem 24.4.1. Let ![]() be linear.
be linear.
Proof. Let, A = ⟨(a1, b1, c1), (i1, j1, k1), (p1, q1, r1)⟩ and B = ⟨(a2, b2, c2), (i2, j2, k2), (p2, q2, r2)⟩ be two SVTNNs and κ be any real number. Then, it has to prove that ![]() . Then,
. Then,


Theorem 24.4.2. If A, B, and C are three arbitrary SVTNNs and A ≲ B and B ≲ C are true, then A ≲ C is true.
Proof. Given that A ≲ B, then ![]() (A) ≤
(A) ≤ ![]() (B) for 0 ≤ λ1, λ2, λ3 ≤ 1. Also, given that B ≲ C, then
(B) for 0 ≤ λ1, λ2, λ3 ≤ 1. Also, given that B ≲ C, then ![]() (B) ≤
(B) ≤ ![]() (C), for 0 ≤ λ1, λ2, λ3 ≤ 1. This implies that
(C), for 0 ≤ λ1, λ2, λ3 ≤ 1. This implies that ![]() (A) ≤
(A) ≤ ![]() (C), for 0 ≤ λ1, λ2, λ3 ≤ 1. Hence, the result follows that A ≲ C.
(C), for 0 ≤ λ1, λ2, λ3 ≤ 1. Hence, the result follows that A ≲ C.
24.5 Numerical Examples
In this section, some numerical examples are discussed to assess how well the proposed method performs.
Example 24.5.1. Consider two SVTNNs A = ⟨(0.50, 0.65, 0.80), (0.10, 0.15, 0.30), (0.10, 0.20, 0.30)⟩, B = ⟨(0.10, 0.20, 0.30), (0.20, 0.30, 0.40), (0.40, 0.50, 0.70)⟩ and three weighted functions be P = (λ1 = 0.3, λ2 = 0.4, λ3 = 0.5), Q = (λ1 = 0.5, λ2 = 0.5, λ3 = 0.5) and S = (λ1 = 1.0, λ2 = 1.0, λ3 = 0.9).
Then, the comparison is between two SVTNNs, A and B, as shown in Table 24.1.
Example 24.5.2. Consider two SVTNNs A = ⟨(0.30, 0.45, 0.50), (0.10, 0.20, 0.40), (0.10, 0.20, 0.30)⟩, B = ⟨(0.20, 0.30, 0.35), (0.10, 0.10, 0.10), (0.60, 0.70, 0.80)⟩ and three weighted functions P = (λ1 = 1.0, λ2 = 1.0, λ3 = 1.0), Q = (λ1 = 0.5, λ2 = 0.5, λ3 = 0.5) and S = (λ1 = 0.1, λ2 = 0.1, λ3 = 0.1).
Then, the comparison is between the two SVTNNs, A and B, as shown in Table 24.2.
Example 24.5.3. Consider two SVTNNs A = ⟨(0.6, 0.7, 0.9), (0.1, 0.3, 0.4), (0.1, 0.4, 0.6)⟩, B = ⟨(0.1, 0.2, 0.3), (0.4, 0.5, 0.6), (0.7, 0.8, 0.9)⟩ and three weighted functions P = (λ1 = 0.3, λ2 = 0.4, λ3 = 0.5), Q = (λ1 = 0.3, λ2 = 0.6, λ3 = 0.5) and S = (λ1 = 0.6, λ2 = 0.4, λ3 = 0.7). Then, the comparison is between the two SVTNNs, A and B, as shown in Table 24.3.
Table 24.1 Ranking of SVNNs in Example 24.5.1.
| λ1,λ2,λ3, | Results | ||
|---|---|---|---|
| 0.3,0.4,0.5 | 0.5217 | 0.5384 | A ≺ B |
| 0.5,0.5,0.5 | 0.5083 | 0.5083 | A ~ B |
| 1.0,1.0,0.9 | 0.4534 | 0.45502 | A ≻ B |
Table 24.2 Ranking of SVNNs in Example 24.5.2.
| λ1,λ2,λ3, | Results | ||
|---|---|---|---|
| 1.0,1.0,1.0 | 0.0669 | 0.5168 | A ≺ B |
| 0.5,0.5,0.5 | 0.4251 | 0.5460 | A ≺ B |
| 0.1,04,0.1 | 0.4719 | 0.5693 | A ≺ B |
Table 24.3 Ranking of SVNNs in Example 24.5.3.
| λ1,λ2,λ3, | Results | ||
|---|---|---|---|
| 0.3,0.4,0.5 | 0.6584 | 0.8101 | A ≺ B |
| 0.3,0.6,0.5 | 0.7550 | 0.7500 | A ≻ B |
| 0.6,0.4,0.7 | 0.7000 | 0.7401 | A ≺ B |
24.6 Conclusion
The majority of real-life decision-making is based on fuzzy numbers due to their language connotations. Ordering fuzzy numbers is much more important in order to solve such difficulties. There are several documented ranking systems for single-valued fuzzy numbers. This paper developed a novel ranking approach for single-valued fuzzy numbers based on convex combinations of the fuzzy numbers’ α, β, and γ cut sets. A number of theorems have also been proved using the proposed method. Furthermore, numerical examples have been provided to demonstrate the suggested strategy’s superior performance. This ranking method may be used to look at the rankings of intuitionistic fuzzy numbers, type-2 fuzzy numbers, hesitant fuzzy numbers, and other fuzzy numbers. Further, this proposed method can be applied to real-life problems like medicine, business, economics, computer sciences, etc.
References
- 1. S. I. A. Aal, M. M. A. A. Ellatif, and M. M. Hassan. Two Ranking Methods of Single Valued Triangular Neutrosophic Numbers to Rank and Evaluate Information Systems Quality, 2018.
- 2. A. Bhaumik, S. Roy, and D.-F. Li. (α, β, γ)-cut set based ranking approach to solving bi-matrix games in neutrosophic environment. Soft Computing, 25:1–11, 02 2021.
- 3. P. Biswas, S. Pramanik, and B. Giri. Value and ambiguity index based ranking method of single-valued trapezoidal neutrosophic numbers and its application to multi-attribute decision making. Neutrosophic Sets and Systems, 12:127–138, 07 2016.
- 4. G. Bortolan and R. Degani. A review of some methods for ranking fuzzy subsets. Fuzzy Sets and Systems, 15(1):1 – 19, 1985.
- 5. M. Brunelli and J. Mezei. How different are ranking methods for fuzzy numbers? a numerical study. International Journal of Approximate Reasoning, 54(5):627 – 639, 2013.
- 6. S. M. Chen. New methods for subjective mental workload assessment and fuzzy risk analysis. Cybernetics and Systems, 27(5):449–472, 1996.
- 7. S.-M. Chen and K. Sanguansat. Analyzing fuzzy risk based on a new fuzzy ranking method between generalized fuzzy numbers. Expert Systems with Applications, 38(3):2163 – 2171, 2011.
- 8. Z. Chen, G. Huang, and A. Chakma. Hybrid fuzzy-stochastic modeling approach for assessing environmental risks at contaminated groundwater systems. Journal of Environmental Engineering, 129(1):79–88, 2003.
- 9. F. Choobineh and H. Li. An index for ordering fuzzy numbers. Fuzzy Sets and Systems, 54(3):287 – 294, 1993.
- 10. R. Chutia. Ranking of fuzzy numbers by using value and angle in the epsilon-deviation degree method. Applied Soft Computing, 60:706 – 721, 2017.
- 11. R. Chutia and B. Chutia. A new method of ranking parametric form of fuzzy numbers using value and ambiguity. Applied Soft Computing, 52:1154 – 1168, 2017.
- 12. R. Chutia, R. Gogoi, and D. Datta. Ranking p-norm generalised fuzzy numbers with different left height and right height using integral values. Mathematical Sciences, 9(1):1–9, 2015.
- 13. I. Deli. Operators on single valued trapezoidal neutrosophic numbers and svtn-group decision making. Neutrosophic Sets and Systems, 22:131–150.
- 14. I. Deli and Y. uba. A ranking method of single valued neutrosophic numbers and its applications to multi-attribute decision making problems. International Journal of Machine Learning and Cybernetics, 8, 08 2017.
- 15. D. Dubois and H. Prade. Fuzzy Sets and Systems: Theory and Applications. Academic Press, Inc., Orlando, FL, USA, 1980.
- 16. T. Garai, H. Garg, and T. Roy. A ranking method based on possibility mean for multi-attribute decision making with single valued neutrosophic numbers. Journal of Ambient Intelligence and Humanized Computing, 11, 11 2020.
- 17. P. Grzegorzewski. Algorithms for trapezoidal approximations of fuzzy numbers preserving the expected interval. Fuzzy Sets and Systems, 159:1354–1364, 06 2008.
- 18. R. Jain. Decisionmaking in the presence of fuzzy variables. IEEE Transactions on Systems, Man and Cybernetics, SMC-6(10):698–703, Oct 1976.
- 19. R. Jain. A procedure for multiple-aspect decision making using fuzzy sets. International Journal of Systems Science, 8(1):1–7, 1977.
- 20. C. Jana, G. Muhiuddin, and M. Pal. Multiple-attribute decision-making problems based on svtnh methods. Journal of Ambient Intelligence and Humanized Computing, 11, 09 2020.
- 21. C. Jana and M. Pal. A robust single-valued neutrosophic soft aggregation operators in multi-criteria decision making. Symmetry, 11(1), 2019.
- 22. C. Jana, M. Pal, F. Karaaslan, and J. Wang. Trapezoidal neutrosophic aggregation operators and their application to the multi-attribute decision-making process. Scientia Iranica, 27(3):1655–1673, 2020.
- 23. F. KARAASLAN. Gaussian single-valued neutrosophic numbers and its application in multi-attribute decision making. Infinite Study, 2018.
- 24. J. Peng, J. Wang, H.-Y. Zhang, and X.-h. Chen. An outranking approach for multi-criteria decision-making problems with simplified neutrosophic sets. Applied Soft Computing, 25:336–346, 12 2014.
- 25. R. A. Shureshjani and M. Darehmiraki. A new parametric method for ranking fuzzy numbers. Indagationes Mathematicae, 24(3):518 – 529, 2013.
- 26. F. Smarandache. Neutrosophy: Neutrosophic Probability, Set, and Logic: Analytic Synthesis & Synthetic Analysis. Analytic Synthesis and Synthetic Analysis Series. American Research Press, 1998.
- 27. F. Smarandache. A unifying field in logics: Neutrosophic logic., 1999.
- 28. F. Smarandache. Neutrosophic set a generalization of the intuitionistic fuzzy set. International Journal of Pure and Applied Mathematics, 24:38–42, 01 2004.
- 29. V. Ulucay, A. Kilic, I. Yildiz, and M. ahin. A new approach for multi-attribute decision-making problems in bipolar neutrosophic sets. Infinite Study, 2018.
- 30. X. Wang and E. E. Kerre. Reasonable properties for the ordering of fuzzy quantities (i). Fuzzy Sets and Systems, 118(3):375 – 385, 2001.
- 31. X. Wang and E. E. Kerre. Reasonable properties for the ordering of fuzzy quantities (ii). Fuzzy Sets and Systems, 118(3):387 – 405, 2001.
- 32. V. F. Yu and L. Q. Dat. An improved ranking method for fuzzy numbers with integral values. Applied Soft Computing, 14, Part C:603 – 608, 2014.
- 33. L. A. Zadeh. Fuzzy sets. Information and Control, 8(3):338–353, 1965.
- 34. H.-Y. Zhang, J. Wang, and X. Chen. An outranking approach for multi-criteria decision-making problems with interval-valued neutrosophic sets. Neural Computing and Applications, 27, 04 2015.
Note
- E-mail: [email protected]
