11
Modelling and Analysis of a Congestion Dependent Queue with Bernoulli Scheduled Vacation Interruption and Client Impatience
K. Jyothsna1⋆ and P. Vijaya Kumar2
1Department of Mathematics, Anil Neerukonda Institute of Technology and Sciences, Visakhapatnam, Andhra Pradesh, India
2Department of Mathematics, GITAM (Deemed to be University), Visakhapatnam, Andhra Pradesh, India
Abstract
This paper’s purpose is to model and analyze an impatient client renewal input Bernoulli scheduled vacation interruption queue. Two types of congestion dependent client impatience, namely balking and reneging, have been incorporated. The server shifts to working vacation mode whenever the system is completely depleted. The server follows Bernoulli’s vacation interruption schedule after executing a service during working vacation, i.e., the server either continues working during the vacation with certain probability or interrupts the working vacation with the complementary probability. Regular service durations, working vacation service durations, and vacation durations are expected to be congestion dependent and exponentially distributed. The stationary probability distributions at different epochs were estimated utilizing supplementary variable and iterative approaches. A few performance metrics and the model parameters’ influence on the performance metrics have been provided through numerical outcomes.
Keywords: Balking, reneging, congestion dependent, multiple working vacations, vacation interruption, Bernoulli schedule
11.1 Introduction
Queues or waiting lines are prominent in normal life and even in a range of corporate and manufacturing contexts. Waiting for service is inescapable, resulting in dissatisfaction, annoyance, and anxiety among clients. Clients are strained for time in today’s fast-paced environment. They would prefer not to be involved in the act of waiting for service. Clients’ behavior is affected by such time limitations. Balking and reneging are two terms used in queuing parlance to describe this type of impatience. If a client on arrival discovers the queueing system is not empty, he or she may elect not to join it. Balking is the term used in queueing theory to describe this behavior. Clients who queue up but leave before the service is completed are termed to be reneged. Clients’ balking behavior in an exponential queueing situation has been initially proposed by Haight [1]. For the single server Markovian problem, Haight [2] introduced the reneging behavior of clients. The research of a balking queue under renewal input process has been conducted by Finch [3]. Wang et al. [4] carried out an optimum and sensitivity analysis as well as a number of numerical experiments on a machine maintenance issue including multiple servers and balking. Ward [5] examined the outcomes as well as the reneging behavior of the queueing problem under traditional high traffic.
Queuing models with server vacations are especially significant for laying the groundwork for effective design and research in a number of real life scenarios like commercial and industrial manufacturing units, software and information networking, and other sectors. Clients cannot access the service facility for a predefined duration of time in vacation queueing approaches. The server may be clearing surplus tasks left by departing clients, undergoing restoration, or taking a break during vacation. Several authors have explored queueing scenarios where the service facility takes a break, see [6–16].
Working vacation queues have gained popularity in the modern generations as a result of possible uses in data transmission, internet technology, industrial systems, and many other associated systems. Servi and Finn [17] presented the idea of working vacations (WV), wherein rather than shutting down altogether, the service facility delivers service to the arrivals at a decreased rate. This process is continued until a waiting client is discovered at a vacation termination instant. A series of such WV is stated as multiple working vacations (MWV). Working vacation queues are more convenient to utilize since they are more accessible than the traditional vacation queues. Due to this, working vacation queueing systems have sparked a lot of interest. Banik et al. [18] published the analysis of an MWV queue, wherein the arrivals follow a renewal process, utilizing a supplementary variable method. A finite buffer balking queue under renewal input process has been reported by Vijaya Laxmi and Jyothsna [19]. Majid [20] worked on the study of client impatience in a working vacation waiting line.
When some system indices reach a specific threshold in WV queues, the server may restore regular service, interrupting the working vacation. This sort of action is referred to as vacation interruption (VI) in working vacation queues. Li and Tian [21] initially came up with the idea of VI in a Markovian queue. Li et al. [22] extended Li and Tian [21]’s research to a VI queue wherein the arrivals follow a renewal process. Majid and Manoharan [23] published the research of a Markovian queue with VI wherein the server is expected to interrupt the WV if the system detects at least N waiting clients at a service finishing moment during the WV. At the moment the service is completed in WV, the server determines whether to extend the WV with a probability of q or to disrupt the WV with the complimentary probability of 1 − q, referred to as Bernoulli scheduled vacation interruption. Initially, Zhang and Shi [24] explored VI under the Bernoulli rule in an exponential queue. The investigations of an impatient client VI queue under Bernoulli rule and renewal input process has been published by Vijaya Laxmi et al. [25]. More information regarding working vacation queues with client impatience may be found in Bouchentouf and Yahiaoui [26], Majid et al. [27], as well as references therein.
The majority of queueing system research is predicated on the notion that the system’s state has no effect on the input and service parameters. In practice, however, many of the queueing system’s service and input parameters are based on the system’s state and reducing the clients wait time. Consider the case of telecommunications network routing. Congestion independent routing probabilities cannot prevent tasks from being sent to already overburdened disc stations in such networks, whereas jobs are routed to the least loaded discs first when congestion dependent routing probabilities are used. State dependent routing outperforms state independent routing in terms of throughput. For literature on state dependent queues, see [28−30] and the references therein.
To our knowledge, no research has ever examined queues that include congestion dependence, working vacations, Bernoulli schedule VI, and impatient clients; this gap in the literature drives the current research. Also, the uncorrelated arrival process often yields a better approximation than the exponential distribution since the memoryless quality of the aforementioned distribution might not necessarily fit the aims of applications and it can incorporate Erlang, deterministic distributions, etc. Hence, investigating the impact of client impatience in a congestion dependent Bernoulli scheduled VI queue under renewal input process is worthwhile. Service, as well as the vacation durations of the service facility, are expected to be exponentially distributed and congestion dependent. The concept is researched employing supplementary variable and iterative techniques. The stationary distribution of the number of clients has been computed at pre-arrival and arbitrary epochs. Performance metrics and numerical data indicating the change in the performance metrics with the model parameters are provided in table and graph forms.
The following is the layout of the article’s main body. Section 11.2 presents the model’s overview. The computation of the stationary distributions at diverse time epochs is in Section 11.3 and special cases of the model in Section 11.4. In Section 11.5, several model performance metrics are provided and numerical calculations to show the parametric influence on system performance metrics are disposed in Section 11.6. Finally, Section 11.7 brings the article to a conclusion.
11.2 Model Overview
A GI/M/1/N/MWV queue that is congestion dependent and having balking, reneging, vacation interruption under a Bernoulli schedule is studied. The time between two subsequent arrivals are assumed to be distributed identically and are independent random variables with probability density function a(z), z ≥ 0, Laplace-Stieltjes transformation (LST) ![]() , and mean inter-arrival duration
, and mean inter-arrival duration ![]() . When a client views j clients in the system, it can queue up with probability βj or balk with the complimentary probability 1 − βj. We also presume that β0 = 1, 0 ≤ βj+1 < βj ≤ 1, 1 ≤ j ≤ N – 1, and βN = 0. If an arrival does not join the queue, he or she will be permanently lost.
. When a client views j clients in the system, it can queue up with probability βj or balk with the complimentary probability 1 − βj. We also presume that β0 = 1, 0 ≤ βj+1 < βj ≤ 1, 1 ≤ j ≤ N – 1, and βN = 0. If an arrival does not join the queue, he or she will be permanently lost.
If an arrival has to wait longer than expected for service after entering the queue, he may renege. With parameter α, the client’s waiting period preceding reneging is exponentially distributed. (j − 1)α is taken as the average reneging rate, as an impatient client’s arrival and departure are unrelated.
A single service facility offers services on a first-come, first-served (FCFS) basis. The service facility departs for a WV as and when the system is depleted. Unlike the queueing paradigms with conventional vacation policy, the service is provided to the waiting clients at a slower rate during WV. At the moment, the service is completed during WV, the server determines whether to extend the vacation with the probability of q or to disrupt the WV with a complimentary probability of 1 − q, designated as Bernoulli scheduled vacation interruption.
When there are j clients in the system, the regular service durations, WV service durations, and vacation durations are all considered to be exponentially distributed with congestion dependent rates µj, ηj and ϕj, 1 ≤ j ≤ N, respectively. Further, define the average regular service rate (µm), average vacation service rate (ηm), and average vacation rate (ϕm) as

At time t, let
- Ns(t) = The total count of clients, counting the one who is currently undergoing service
- Z(t) = Upcoming arrival’s remaining inter-arrival time.
At steady state, define:

The Laplace-Stieltjes transformations that follow are introduced:
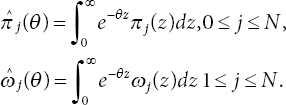
At an arbitrary instant, while the server is in WV and regular service, the probability of j clients in the system can be denoted by ![]() and
and ![]() respectively.
respectively.
11.3 Model Analysis
To determine the system length probabilities at arbitrary instants, differential difference equations are formulated that associate the distribution of number of clients in the system at the completion of the vacation and regular service period. We accomplish this by employing the supplementary variable technique, which connects the system’s state at two time instants t and t+dt. The differential difference equations under steady-state conditions can be constructed utilizing probabilistic reasonings and taking limit t → ∞ as
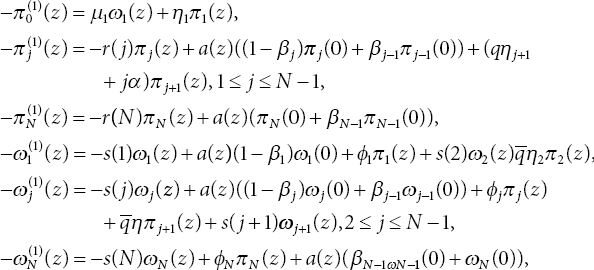
where πj(0) and ωj(0) are respective rates of arrivals and for 1 ≤ j ≤ N, r(j) = ϕj + ηj +(j − 1)α, s(j) = µj + (j − 1)α. The preceding set of equations is multiplied with e−θz and integrated over z for 0 to ∞ to get
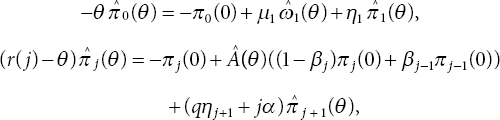
Adding the above equations results as:

Assigning θ → 0 and utilizing the normality condition ![]()
![]() produces
produces
11.3.1 Pre-Arrival Epoch Probabilities
Let ![]() and
and ![]() symbolize the probability of j clients in the system during WV and during regular service period, respectively, at pre-arrival instant. Applying Bayes’ theorem, we have
symbolize the probability of j clients in the system during WV and during regular service period, respectively, at pre-arrival instant. Applying Bayes’ theorem, we have
To obtain the pre-arrival instant probabilities ![]() we need to evaluate the rate probabilities (πj(0), ωj(0)) as shown below.
we need to evaluate the rate probabilities (πj(0), ωj(0)) as shown below.
Taking θ = r(N) in Equation (11.3) gives
where 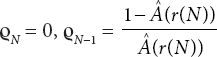 . Substituting πN−1 (0) in (11.3), we get
. Substituting πN−1 (0) in (11.3), we get
where

with

Taking θ = r(j) in (11.2) and proceeding as above, we obtain
where

and
where

with
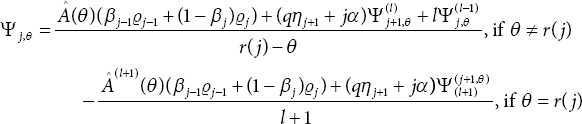
Taking θ = s(N) in (11.6), we have ωN−1(0) in terms of πN (0) and ωN (0) as
where
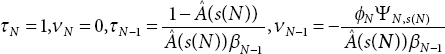
Substituting (11.11) in (11.6) gives
where
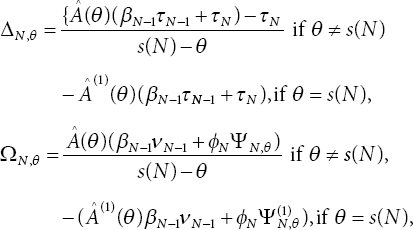
with
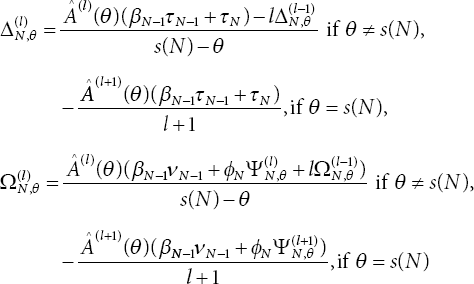
From Equation (11.5), we get ωj(0), ![]() in terms of πN (0) and ωN (0) as
in terms of πN (0) and ωN (0) as
where for 2 ≤ j ≤ N − 1,
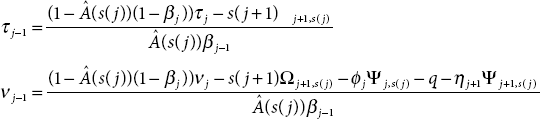
and
where for 2 ≤ j ≤ N − 1,
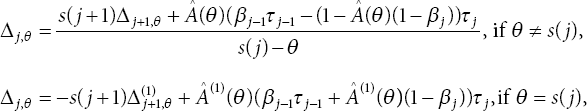

with

Setting θ = s(1) in (11.4) yields ωN (0) in terms of πN (0) as
where
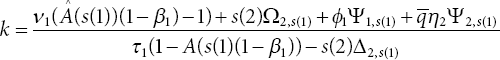
Lastly, (11.7) yields the remaining unknown πN(0) as
Theorem 11.1. The probabilities ![]() and
and ![]() at pre-arrival epoch are determined as follows:
at pre-arrival epoch are determined as follows:

Proof. Using (11.8) and (11.13) in (11.9) to (11.12), we obtain the result of the theorem.
11.3.2 Arbitrary Epoch Probabilities
In this subsection, the pre-arrival probabilities ![]() and
and ![]() are used to derive the arbitrary epoch probabilities πj (0 ≤ j ≤ N ) and ωj (1 ≤ j ≤ N ).
are used to derive the arbitrary epoch probabilities πj (0 ≤ j ≤ N ) and ωj (1 ≤ j ≤ N ).
This is treated as a theorem given below.
Theorem 11.2. The probabilities at the arbitrary epoch are obtained as

Proof. The intended outcome of the theorem is obtained by placing θ = 0 in Equations (11.2) to (11.6), utilizing (11.8) and the normalization condition.
11.4 Special Cases
Case 1: Taking q = 1, α = 0, and βj = 1 for 1 ≤ j ≤ N − 1, the present model reduces to GI/M (n)/1/N queue with MWV and the findings are consistent with Goswami et al. [28].
Case 2: Setting q = 1, µj = µ, ηj = η, ϕj = ϕ ∀ j = 1, 2,... , N and setting α,= 0, the current model is reduced to a GI/M/1/N/MWV queue with balking. Our findings are identical to Vijaya Laxmi and Jyothsna [19] in this situation.
Case 3: Taking q = 1, the current model gets reduced to GI/M (n)/1/N/ MWV queue with balking and reneging and the outcomes are consistent with Vijaya Laxmi and Jyothsna [29].
Case 4: Taking µj = µ, ηj = η, ϕj = ϕ ∀ j = 1, 2,... , N brings down our model to a GI/M/1/N/MWV queue with balking, reneging, and Bernoulli scheduled VI. The results are consistent with Vijaya Laxmi et al. [25].
Case 5: Taking q = 1, µj = µ, ηj = η, ϕj = ϕ, βj = 1 ∀ j = 1, 2,... , N and α,= 0 lowers the current model to GI/M/1/N/MWV queue. The results match with Banik et al. [18].
Case 6: Setting q = 1, µj = µ, ηj = 0, ϕj = ϕ ∀ j = 1, 2,... , N and taking α,= 0, βj = 1 for 1 ≤ j ≤ N, our numerical findings correspond to GI/M/1/N queue with multiple vacations (Karaes-man and Gupta) [7].
Case 7: Taking q = 1, µj = µ, ηj = 0, ϕj → ∞ ∀ j = 1, 2,... , N and setting α = 0 the current model becomes a renewal input balking queue. The working vacation probabilities πj(1 ≤ j ≤ N) do not occur in this situation and our outcomes agree with Finch [3] (GI/M/1/N queue with balking).
11.5 Performance Metrics
The performance metrics of the model can be assessed upon obtaining the state probabilities at pre-arrival and arbitrary instants. The expected system length (Ls), the blocking probability (Pl), and the expected waiting duration in the system (Ws) of a client employing Little’s Rule are, respectively, given by:

where λe = 1 − Pl represents the effective arrival rate.
The mean rate of balking (br), the mean rate of reneging (rr), and the mean rate of client loss (lr) are measured by

11.6 Numerical Outcomes
This section shows how the performance metrics respond to the changes in model parameters. The model parameters are selected at random as N,= 10, λ = 1.5, α = 0.7, and q = 0.4 and the balking function is considered as βj = 1−j/N 2 with the assumption that β0 = 1 and βN = 0. The congestion dependent rates are assumed to be µj = 0.4j, ηj = 0.2j, and ϕj = 0.1j with averages µm = 2.2, ηm = 1.1, and ϕm = 0.55, respectively. For HE2 inter-arrival time distribution, we have chosen σ1 = 0.149883, σ2 = 0.850117, λ1 = 0.484237, and λ2 = 2.380330.
In Table 11.1, we have presented the values of Ls, Ws, Pl, br, rr, and lr for the following balking functions: βj = 1 − j/N2, βj = 1/(j + 1), and βj = e−j. The mean balking rate (br) is lowest for the balking function βj = 1 − j/N2, as noticed in the table, which in turn results in least mean rate of client loss (lr). This supports our decision to use βj = 1 − j/N 2 as the balking function.
Table 11.1 Numerical values of performance metrics for different balking functions.
| βt = 1 − j/N2 | βj = 1/(j + 1) | βj = e−j | |
|---|---|---|---|
| Ls | 2.008288 | 1.343753 | 1.191490 |
| Ws | 1.338865 | 0.895836 | 0.794326 |
| Pl | 0.000004 | 0.000000 | 0.000000 |
| br | 0.030131 | 0.772889 | 0.940714 |
| rr | 0.754335 | 0.314381 | 0.214521 |
| lr | 0.784466 | 1.087270 | 1.155234 |
Figure 11.1 and Figure 11.2 show the influence of λ on the expected system length (Ls) and the mean rate of client loss (lr) for exponential inter-arrival time distribution, respectively, for different q. The images show that as λ is increased, both Ls and lr grow for any q. Furthermore, for a fixed λ, Ls and lr rise as q increases, meaning that Ls and lr are the least in VI queues when compared to queues with no vacation interruption.
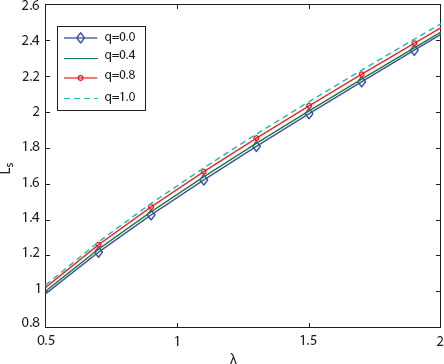
Figure 11.1 Influence of λ on Ls.

Figure 11.2 Effect of λ on lr.
The impact of mean regular service rate (µm) on the expected system length (Ls) and on the expected waiting duration (Ws) are displayed in Figure 11.3 and Figure 11.4, respectively, for different mean vacation rates (ϕm), wherein the inter-arrival durations are considered to be Erlang-5 distributed. As expected, Ls and Ws deplete with the increase of µm for any ϕm. A similar effect is seen on Ls and Ws with the increase of ϕm for fixed µm.
Figures 11.5 and 11.6 show the changes in lr and Ws, respectively, while the inter-arrival times are distributed according to deterministic distribution for different ηm and ϕm. It is worth noting that as ηm and ϕm grow, lr and Ws deplete.
For different inter-arrival time distributions, Figure 11.7 displays the system capacity (N) versus the blocking probability (Pl). The blocking probability (Pl) is lowest when the inter-arrival durations are distributed according to deterministic distribution and highest when they are distributed according to HE2 distribution.
When inter-arrival durations are exponentially distributed, the impact of the reneging rate (α) on the expected system length (Ls) and on the mean rate of client loss (lr) is depicted in Figure 11.8. As visualized in the graph, the expected system length falls as α grows, but the mean rate of client loss increases with α, as would be predicted.
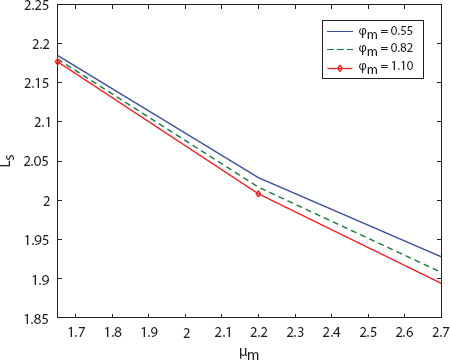
Figure 11.3 Impact of µm on Ls.

Figure 11.4 Impact of µm on Ws.
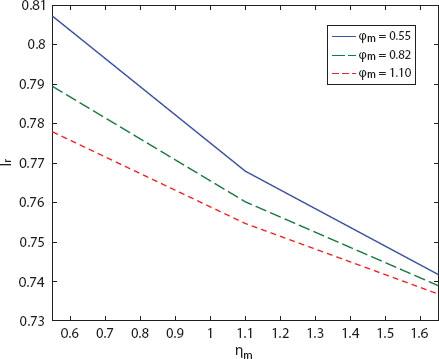
Figure 11.5 Change in lr with ηm.

Figure 11.6 Change in Ws with ηm.
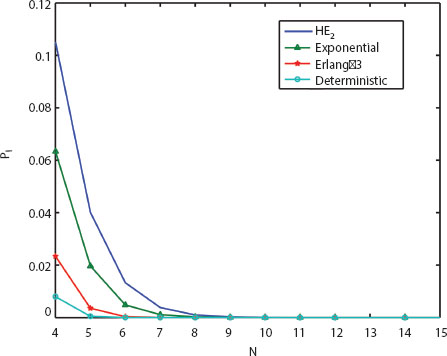
Figure 11.7 N versus Pl.

Figure 11.8 α versus Ls and lr.
11.7 Conclusion
The current research work examines a finite capacity renewal input congestion dependent queue with Bernoulli scheduled vacation interruption and client impatience. The regular service rates, working vacation service rates, and vacation rates are considered to be exponentially distributed and are congestion dependent. To obtain the stationary probabilities at various epochs, we have adopted supplementary variable and iterative techniques. We also presented a few numerical simulations to show the consequence of the model parameters on the key metrics, which are provided in table and graph forms. The current findings would be beneficial and significant for modelling the transportation business, manufacturing systems, medical administration, etc. The future direction of this work would be to expand the model under examination by incorporating state dependent inter-arrival times.
References
- 1. F. A. Haight, Queueing with balking (1957), Biometrika, vol.44, issue.3-4, pp.360-369, https://doi.org/10.1093/biomet/44.3-4.360
- 2. F. A. Haight, Queueing with reneging (1959), Metrika, vol.2, isuue.1, pp.186-197, https://doi.org/10.1007/BF02613734.
- 3. Finch, P.D., Balking in the queueing system GI/M/1 (1959), Acta Mathematica Hungarica, vol.10, issue.1, pp.241-247, https://doi.org/10.1007/BF02063302.
- 4. Kuo-Hsiung Wang, Yuh-Ching Liou and Dong-Yuh Yang, Cost optimization and sensitivity analysis of the machine repair problem with variable servers and balking (2011), Procedia–Social and Behavioral Sciences, vol.25, issue.14, pp.178-188, DOI: 10.1016/j.sbspro.2011.10.539
- 5. Amy R. Ward, Asymptotic analysis of queueing systems with reneging: A survey of results for FIFO, single class models, (2012) Surveys in Operations Research and Management Science, vol. 17, issue.1, pp.1-14, https://doi.org/10.1016/j.sorms.2011.08.002
- 6. Takagi, H. (1991). Queueing Analysis: A Foundation of Performance Evaluation, Vacation and Priority Systems, Vol. 1. Elsevier, Amsterdam.
- 7. Fikri Karaesmen, Surendra M. Gupta. The finite capacity GI/M/1 queue with server vacations (1996), Journal of the Operational Research Society, vol.47, issue.6, pp.817-828, https://doi.org/10.1057/jors.1996.101
- 8. Naishuo Tian, Zhe George Zhang (2006). Vacation Queueing Models: Theory and Applications. International Series in Operations Research and Management Science, Springer, New York.
- 9. Eitan Altman, Uri Yechiali, Analysis of customers’ impatience in queues with server vacations (2006), Queueing Systems, vol.52, issue.4, pp.261-279, https://doi.org/10.1007/s11134-006-6134- x
- 10. Dequan Yue, Wuyi Yue, Yanping Sun, ‘Performance analysis of an M/M/c/N queueing system with balking, reneging and synchronous vacations of partial servers’ in 2006 The Sixth International Symposium on Operations Research and Its Applications, Xinjiang, China, ORSC and APORC, 128-143.
- 11. Uri Yechiali, Queues with system disasters and impatient customers when system is down (2007), Queueing Systems, vol.56, pp.195-202, http://dx.doi.org/10.1007/s11134-007-9031-z
- 12. Eitan Altman, Uri Yechiali, Infinite-server queues with system’s additional task and impatient customers (2008), Probability in the Engineering and Information Sciences, vol.22, issue.4, pp.477-493, http://dx.doi.org/10.1017/S0269964808000296
- 13. Nir Perel, Uri Yechiali, Queues with slow servers and impatient customers (2010), European Journal of Operational Research, vol.201, issue.1, pp.247-258, doi:10.1016/j.ejor.2009.02.024
- 14. Dequan Yue, Wuyi Yue, Zsolt Saffer and Xiaohong Chen, Analysis of an M/M/1 queueing system with impatient customers and a variant of multiple vacation policy (2014), Journal of Industrial and Management Optimization, vol.10, issue.1, pp.89-112, http://dx.doi.org/10.3934/jimo.2014.10.8915. Amina Angelika Bouchentouf, Abdelhak Guendouzi, Cost optimization analysis for an MX/M/c vacation queueing system with waiting servers and impatient customers (2019), SeMA Journal, vol.76, issue.2, pp.309-341, http://dx.doi.org/10.1007.
- 16. M. I. G. Suranga Sampath, Jicheng Liu, Impact of customers’ impatience on an M/M/1 queueing system subject to differentiated vacations with a waiting server (2020), Quality Technology and Quantitative Management, vol.17, issue.2, pp.125-148, https://doi.org/10.1080/16843703.2018.1555877
- 17. L. D. Servi, S. G. Finn, M/M/1 queue with working vacations (M/M/1/ WV) (2002), Performance Evaluation, vol.50, issue.1, pp.41–52, https://doi.org/10.1016/S0166-5316(02)00057-3.
- 18. A. D. Banik, U. C. Gupta, S. S. Pathak, On the GI/M/1/N queue with multiple working vacations - analytic analysis and computation (2007), Applied Mathematical Modelling, vol.31, issue.9, pp.1701-1710, https://doi.org/10.1016/j.apm.2006.05.010
- 19. P. Vijaya Laxmi, K. Jyothsna, Analysis of finite buffer renewal input queue with balking and multiple working vacations (2013), OPSEARCH, vol.50, issue.(4), pp. 548-565. http://dx.doi.org/10.1007/s12597-013-0123-8
- 20. Shakir Majid, Performance analysis of a Markovian queue with impatient customers and working vacation (2021), Journal of the Operations Research Society of China, https://doi.org/10.1007/s40305-021-00361-w.
- 21. Jihong Li, Naishuo Tian, The M/M/1 queue with working vacations and vacation interruption (2007), Journal of Systems Science and Systems Engineering, vol.16, pp.121-127, https://doi.org/10.1007/s11518-006-5030-6
- 22. Ji-HongLi, Nai-Shuo Tian, Zhan-You Ma, Performance analysis of GI/M/1 queue with working vacations and vacation interruption (2008), Applied Mathematical Modelling, vol.32, issue.12, pp.2715-2730, https://doi.org/10.1016/j.apm.2007.09.017
- 23. Shakir Majid and P. Manoharan, Analysis of an M/M/1 queue with working vacation and vacation interruption (2019), Applications and Applied Mathematics: An International Journal, vol.14, issue.1, pp.19-33,
- 24. Hongbo Zhang, Dinghua Shi, The M/M/1 queue with Bernoulli-schedule-controlled vacation and vacation interruption (2009), International Journal of Information and Management Sciences, vol.20, issue.(4), pp.579-587.
- 25. Pikkala Vijaya Laxmi, Singuluri Indira and Kanithi Jyothsna, Ant colony optimization for optimum service times in a Bernoulli schedule vacation interruption queue with balking and reneging (2016), Journal of Industrial and Management Optimization, vol.12, issue.4, pp.1199–1214, http://dx.doi.org/10.3934/jimo.2016.12.1199
- 26. Bochentouf, A. A., Yahiaoui, L. (2017). On feedback queueing system with reneging and retention of reneged customers, multiple working vacations and Bernoulli schedule vacation interruption, Arabian Journal of Mathematics, 6(1), 1-11.
- 27. Shakir Majid, P. Manoharan and A. Ashok, Analysis of an M/M/1 queueing system with working vacation and impatient customers, American International Journal of Research in Science, Technology, Engineering & Mathematics (2019), Special Issue, pp.314-322,
- 28. V. Goswami, P. Vijaya Laxmi, K. Jyothsna, Analysis of GI/M (n)/1/N queue with state-dependent multiple working vacations (2013), OPSEARCH, vol.50, issue.1, pp.106-124, http://dx.doi.org/10.1007/s12597-012-0096-z
- 29. Pikkala Vijaya Laxmi and Kanithi Jyothsna, On renewal input state dependent working vacations queue with impatient customers (2015), International Journal of Mathematics in Operational Research, vol.7, issue.6, pp.661–680.
- 30. Doo Il Choi, Dae-Eun Lim, Analysis of the state-dependent queueing model and its application to battery swapping and charging stations (2020), Sustainability, vol.12(6), issue.2343, pp.1-15, https://doi.org/10.3390/su12062343
Note
- ⋆ Corresponding author: [email protected]