4.3. Laminar Flame Speed

Search in book...
Toggle Font Controls
Create new playlist

Name your new playlist

Playlist description (optional)
Sign In

Email address

Password

Forgot Password?

or

Continue with Facebook

Continue with Google
Sign Up

Full Name

Email address

Confirm Email Address

Password

or

Continue with Facebook

Continue with Google

4.3. Laminar Flame Speed

The flame velocity—also called the burning velocity, normal combustion velocity, or laminar flame speed—is more precisely defined as the velocity at which unburned gases move through the combustion wave in the direction normal to the wave surface.

The initial theoretical analyses for the determination of the laminar flame speed fell into three categories: thermal theories, diffusion theories, and comprehensive theories. The historical development followed approximately the same order.

The thermal theories date back to Mallard and Le Chatelier [3], who proposed propagation of heat back through layers of gas is the controlling mechanism in flame propagation. As one would expect, a form of the energy equation is the basis for the development of the thermal theory. Mallard and Le Chatelier postulated (as shown in Figure 4.4) that a flame consists of two zones separated at the point where the next layer ignites. Unfortunately, this thermal theory requires the concept of an ignition temperature. But adequate means do not exist for the determination of ignition temperatures; moreover, an actual ignition temperature does not exist in a flame.

Later, there were improvements in the thermal theories. Probably the most significant of these is the theory proposed by Zeldovich and Frank-Kamenetskii. Because their derivation was presented in detail by Semenov [4], it is commonly called the Semenov theory. These authors included the diffusion of molecules as well as heat, but did not include the diffusion of free radicals or atoms. As a result, their approach emphasized a thermal mechanism and was widely used in correlations of experimental flame velocities. As in the Mallard–Le Chatelier theory, Semenov assumed an ignition temperature, but by approximations eliminated it from the final equation to make the final result more useful. This approach is similar to what is now termed activation energy asymptotics.

The theory was advanced further when it was postulated that the reaction mechanism can be controlled not only by heat, but also by the diffusion of certain active species such as radicals. As described in the preceding section, low–atomic and molecular weight particles can readily diffuse back and initiate further reactions.

Figure 4.4 Mallard–Le Chatelier description of the temperature in a laminar flame wave.

The theory of particle diffusion was first advanced in 1934 by Lewis and von Elbe [5] in dealing with the ozone reaction. Tanford and Pease [6] carried this concept further by postulating that the diffusion of radicals is all-important, not the temperature gradient as required by the thermal theories. They proposed a diffusion theory that was different in physical concept from the thermal theory. However, one should recall that the equations that govern mass diffusion are the same as those that govern thermal diffusion.

These theories fostered a great deal of experimental research to determine the effect of temperature and pressure on the flame velocity and thus to verify which of the theories were correct. In the thermal theory, the higher the ambient temperature, the higher is the final temperature and therefore the faster is the reaction rate and flame velocity. Similarly, in the diffusion theory, the higher the temperature, the greater is the dissociation, the greater is the concentration of radicals to diffuse back, and therefore the faster is the velocity. Consequently, data obtained from temperature and pressure effects did not give conclusive results.

Some evidence appeared to support the diffusion concept, since it seemed to best explain the effect of H₂O on the experimental flame velocities of CO–O₂. As described in the previous chapter, it is known that at high temperatures water provides the source of hydroxyl radicals to facilitate rapid reaction of CO and O₂.

Hirschfelder et al. [7] reasoned that no dissociation occurs in the cyanogen–oxygen flame. In this reaction the products are solely CO and N₂, no intermediate species form, and the C=O and N≡N bonds are difficult to break. It is apparent that the concentration of radicals is not important for flame propagation in this system, so one must conclude that thermal effects predominate. Hirschfelder et al. [7] essentially concluded that one should follow the thermal theory concept while including the diffusion of all particles, both into and out of the flame zone.

In developing the equations governing the thermal and diffusional processes, Hirschfelder obtained a set of complicated nonlinear equations that could be solved only by numerical methods. To solve the set of equations, Hirschfelder had to postulate some heat sink for a boundary condition on the cold side. The need for this sink was dictated by the use of the Arrhenius expressions for the reaction rate. The complexity is that the Arrhenius expression requires a finite reaction rate even at x = −∞, where the temperature is that of the unburned gas.

To simplify the Hirschfelder solution, Friedman and Burke [8] modified the Arrhenius reaction rate equation so the rate was zero at T = T₀, but their simplification also required numerical calculations.

Then it became apparent that certain physical principles could be used to simplify the complete equations so they could be solved relatively easily. Such a simplification was first carried out by von Karman and Penner [9]. Their approach was considered one of the more significant advances in laminar flame propagation, but it could not have been developed and verified if it were not for the extensive work of Hirschfelder and his collaborators. The major simplification that von Karman and Penner introduced is the fact that the eigenvalue solution of the equations is the same for all ignition temperatures, whether or not it is near T_f. More recently, asymptotic analyses have been developed that provide formulas with greater accuracy and further clarification of the wave structure. These developments are described in detail in three books [10–12].

It is easily recognized that any exact solution of laminar flame propagation must make use of the basic equations of fluid dynamics modified to account for the liberation and conduction of heat and for changes of chemical species within the reaction zones. By use of certain physical assumptions and mathematical techniques, the equations have been simplified. Such assumptions have led to many formulations (see Refs [10–12]), but the theories that will be considered here are an extended development of the simple Mallard–Le Chatelier approach and the Semenov approach. The Mallard–Le Chatelier development is given because of its historical significance and because this simple thermal analysis readily permits the establishment of the important parameters in laminar flame propagation that are more difficult to interpret in the complex analyses. The Zeldovich–Frank-Kamenetskii–Semenov theory is reviewed because certain approximations related to the ignition temperature that are employed are useful in other problems in the combustion field and permit an introductory understanding to activation energy asymptotics.

4.3.1. Theory of Mallard and Le Chatelier

Conceptually, Mallard and Le Chatelier stated that the heat conducted from zone II in Figure 4.4 is equal to that necessary to raise the unburned gases to the ignition temperature (the boundary between zones I and II). If it is assumed that the slope of the temperature curve is linear, the slope can be approximated by the expression [(T_f − T_i)/δ], where T_f is the final or flame temperature, T_i is the ignition temperature, and δ is the thickness of the reaction zone. The enthalpy balance then becomes:

$\dot{m} c_{p} (T_{i} - T_{0}) = λ \frac{(T_{f} - T_{i})}{δ} A$ $\dot{m} c_{p} (T_{i} - T_{0}) = λ \frac{(T_{f} - T_{i})}{δ} A$

(4.8)

where λ is the thermal conductivity,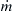

\dot{m}

$\dot{m}$

is the mass rate of the unburned gas mixture into the combustion wave, T₀ is the temperature of the unburned gases, and A is the cross-sectional area taken as unity. Since the problem as described is fundamentally one-dimensional,

$\dot{m} = ρ u A = ρ S_{L} A$ $\dot{m} = ρ u A = ρ S_{L} A$

(4.9)

where ρ is the density, u is the velocity of the unburned gases, and S_L is the symbol for the laminar flame velocity. Because the unburned gases enter normal to the wave, by definition

$S_{L} = u$ $S_{L} = u$

(4.10)

Equation (4.8) then becomes

$ρ S_{L} c_{p} (T_{i} - T_{0}) = λ (T_{f} - T_{i}) / δ$ $ρ S_{L} c_{p} (T_{i} - T_{0}) = λ (T_{f} - T_{i}) / δ$

(4.11)

$S_{L} = (\frac{λ (T_{f} - T_{i})}{ρ c_{p} (T_{i} - T_{0})} \frac{1}{δ})$ $S_{L} = (\frac{λ (T_{f} - T_{i})}{ρ c_{p} (T_{i} - T_{0})} \frac{1}{δ})$

(4.12)

Equation (4.12) is the expression for the flame speed obtained by Mallard and Le Chatelier. Unfortunately, in this expression δ is not known; therefore, a better representation is required.

Since δ is the reaction zone thickness, it is possible to relate δ to S_L. The total rate of mass per unit area entering the reaction zone must be the mass rate of consumption in that zone for the steady flow problem being considered. Thus,

$\dot{m} / A = ρ u = ρ S_{L} = \dot{ω} δ$ $\dot{m} / A = ρ u = ρ S_{L} = \dot{ω} δ$

(4.13)

where

\dot{ω}

$\dot{ω}$

specifies the reaction rate in terms of concentration (in grams per cubic centimeter) per unit time. Equation (4.12) for the flame velocity then becomes

$S_{L} = {[\frac{λ}{ρ c_{p}} \frac{(T_{f} - T_{i})}{(T_{i} - T_{0})} \frac{\dot{ω}}{ρ}]}^{1 / 2} \sim {(α \frac{\dot{ω}}{ρ})}^{1 / 2}$ $S_{L} = {[\frac{λ}{ρ c_{p}} \frac{(T_{f} - T_{i})}{(T_{i} - T_{0})} \frac{\dot{ω}}{ρ}]}^{1 / 2} \sim {(α \frac{\dot{ω}}{ρ})}^{1 / 2}$

(4.14)

where it is important to understand that ρ is the unburned gas density and α is the thermal diffusivity. More fundamentally the mass of reacting fuel mixture consumed by the laminar flame is represented by

$ρ S_{L} \sim {(\frac{λ}{c_{p}} \dot{ω})}^{1 / 2}$ $ρ S_{L} \sim {(\frac{λ}{c_{p}} \dot{ω})}^{1 / 2}$

(4.15)

Combining Eqns (4.13) and (4.15), one finds that the reaction thickness in the complete flame wave is

$δ \sim α / S_{L}$ $δ \sim α / S_{L}$

(4.16)

This adaptation of the simple Mallard–LeChatelier approach is most significant in that the result

$S_{L} \sim {(α \frac{\dot{ω}}{ρ})}^{1 / 2}$ $S_{L} \sim {(α \frac{\dot{ω}}{ρ})}^{1 / 2}$

is useful in estimating the laminar flame phenomena as various physical and chemical parameters are changed.

Linan and Williams [13] reviewed the description of the flame wave offered by Mikhelson [14], who equated the heat release in the reaction zone to the conduction of energy from the hot products to the cool reactants. Since the overall conservation of energy shows that the energy per unit mass (h) added to the mixture by conduction is

$h = c_{p} (T_{f} - T_{0})$ $h = c_{p} (T_{f} - T_{0})$

(4.17)

then

$h \dot{ω} δ_{L} = λ (T_{f} - T_{0}) / δ_{L}$ $h \dot{ω} δ_{L} = λ (T_{f} - T_{0}) / δ_{L}$

(4.18)

In this description δ_L represents not only the reaction zone thickness δ in the Mallard–Le Chatelier consideration, but also the total of zones I and II in Figure 4.4. Substituting Eqn (4.17) into Eqn (4.18) gives

$c_{p} (T_{f} - T_{0}) \dot{ω} δ_{L} = λ (T_{f} - T_{0}) / δ_{L}$ $c_{p} (T_{f} - T_{0}) \dot{ω} δ_{L} = λ (T_{f} - T_{0}) / δ_{L}$

$δ_{L} = {(\frac{λ}{c_{p}} \frac{1}{\dot{ω}})}^{1 / 2}$ $δ_{L} = {(\frac{λ}{c_{p}} \frac{1}{\dot{ω}})}^{1 / 2}$

The conditions of Eqn (4.13) must hold, so that in this case,

$ρ S_{L} = \dot{ω} δ_{L}$ $ρ S_{L} = \dot{ω} δ_{L}$

(4.19)

and Eqn (4.18) becomes

$S_{L} = {(\frac{λ}{ρ c_{p}} \frac{\dot{ω}}{ρ})}^{1 / 2} = {(α \frac{\dot{ω}}{ρ})}^{1 / 2}$ $S_{L} = {(\frac{λ}{ρ c_{p}} \frac{\dot{ω}}{ρ})}^{1 / 2} = {(α \frac{\dot{ω}}{ρ})}^{1 / 2}$

(4.20)

Whereas the proportionality of Eqn (4.14) is the same as the equality in Eqn (4.20), the difference in the two equations is the temperature ratio.

${(\frac{T_{f} - T_{i}}{T_{i} - T_{0}})}^{1 / 2}$ ${(\frac{T_{f} - T_{i}}{T_{i} - T_{0}})}^{1 / 2}$

In the next section, the flame speed development of Zeldovich, Frank–Kamenetskii, and Semenov will be discussed. They essentially evaluate this term to eliminate the unknown ignition temperature T_i by following what is now the standard procedure of narrow reaction zone asymptotics, which assumes that the reaction rate decreases rapidly with a decrease in temperature. Thus, in the course of the integration of the rate term

\dot{ω}

$\dot{ω}$

in the reaction zone, they extend the limits over the entire flame temperature range, T₀ to T_f. This approach is, of course, especially valid for large activation energy chemical processes, which are usually the norm in flame studies. Anticipating this development, one finds that the temperature ratio term essentially becomes

$\frac{R T_{f}^{2}}{E (T_{f} - T_{0})}$ $\frac{R T_{f}^{2}}{E (T_{f} - T_{0})}$

This term specifies the ratio δ_L/δ and was determined explicitly by Linan and Williams [13] by the procedure they called activation energy asymptotics. Essentially, this is the technique used by Zeldovich, Frank–Kamenetskii, and Semenov (see Eqn (4.60)). The analytical development of the asymptotic approach is not given here. For a discussion of the use of asymptotics, one should refer to the excellent books by Williams [12], Linan and Williams [13], and Zeldovich et al. [10]. Linan and Williams called the term

R T_{f}^{2} / E (T_{f} - T_{0})

$R T_{f}^{2} / E (T_{f} - T_{0})$

the Zeldovich number and gave this number the symbol β in their book. Thus,

$β = (δ_{L} / δ)$ $β = (δ_{L} / δ)$

It follows, then, that Eqn (4.14) may be rewritten as

$S_{L} = {(\frac{α}{β} \frac{\dot{ω}}{ρ})}^{1 / 2}$ $S_{L} = {(\frac{α}{β} \frac{\dot{ω}}{ρ})}^{1 / 2}$

(4.21)

and, from the form of Eqn (4.19), that

$δ_{L} = β δ = \frac{α β}{S_{L}}$ $δ_{L} = β δ = \frac{α β}{S_{L}}$

(4.22)

The general range of hydrocarbon–air premixed flame speeds falls around 40 cm/s. Using a value of thermal diffusivity evaluated at a mean temperature of 1300 K, one can estimate δ_L to be close to 0.1 cm. Thus, hydrocarbon–air flames have a characteristic length of the order of 1 mm. The characteristic time is

(α {/S}_{L}^{2})

$(α {/S}_{L}^{2})$

, and for these flames this value is estimated to be of the order of a few milliseconds. If one assumes that the overall activation energy of the hydrocarbon–air process is of the order 160 kJ/mol and that the flame temperature is 2100 K, then β is about 10, and probably somewhat less in actuality. Thus, it is estimated from this simple physical approach that the reaction zone thickness, δ, would be a small fraction of a millimeter.

The simple physical approaches proposed by Mallard and Le Chatelier [3] and Mikhelson [14] offer significant insight into the laminar flame speed and factors affecting it. Modern computational approaches now permit not only the calculation of the flame speed, but also a determination of the temperature profile and composition changes throughout the wave. These computational approaches are only as good as the thermochemical, transport, and kinetic reaction rate parameters that form their data base. Since these approaches include simultaneous chemical rate processes and species diffusion, they are referred to as comprehensive theories, which is the topic of Section 4.3.3.

Equation (4.21) permits one to establish various trends of the flame speed as various physical parameters change. Consider, for example, how the flame speed should change with a variation of pressure. If the rate term

\dot{ω}

$\dot{ω}$

follows second-order kinetics, as one might expect from a hydrocarbon–air system, then the concentration terms in

\dot{ω}

$\dot{ω}$

would be proportional to P². However, the density term in α (= λ/ρc_p) and the other density term in Eqn (4.21) also give a P² dependence. Thus for a second-order reaction system the flame speed appears independent of pressure. A more general statement of the pressure dependence in the rate term is that

\dot{ω} \sim P^{n}

$\dot{ω} \sim P^{n}$

, where n is the overall order of the reaction. Thus, it is found that

$S_{L} \sim {(P^{n - 2})}^{1 / 2}$ $S_{L} \sim {(P^{n - 2})}^{1 / 2}$

(4.23)

For a first-order dependence such as that observed for a hydrazine decomposition flame, S_L ∼ P^−1/2. As will be shown in Section 4.3.5, although hydrocarbon–air oxidation kinetics are approximately second-order, many hydrocarbon–air flame speeds decrease as the pressure rises. This trend is due to the increasing role of the third-order reaction H + O₂ + M → HO₂ + M in effecting the chain branching and slowing the rate of energy release. Although it is now realized that S_L in these hydrocarbon systems may decrease with pressure, it is important to recognize that the mass burning rate ρS_L increases with pressure. Essentially, then, one should note that

${\dot{m}}_{0} \equiv ρ S_{L} \sim P^{n / 2}$ ${\dot{m}}_{0} \equiv ρ S_{L} \sim P^{n / 2}$

(4.24)

where

{\dot{m}}_{0}

${\dot{m}}_{0}$

is the mass flow rate per unit area of the unburned gases. Considering β a constant, the flame thickness δ_L decreases as the pressure rises since

$δ_{L} \sim \frac{α}{S_{L}} \sim \frac{λ}{c_{p} ρ S_{L}} \sim \frac{λ}{c_{p} {\dot{m}}_{0}}$ $δ_{L} \sim \frac{α}{S_{L}} \sim \frac{λ}{c_{p} ρ S_{L}} \sim \frac{λ}{c_{p} {\dot{m}}_{0}}$

(4.25)

Since (λ/c_p) does not vary with pressure and

{\dot{m}}_{0}

${\dot{m}}_{0}$

increases with pressure as specified by Eqn (4.24), Eqn (4.25) verifies that the flame thickness must decrease with pressure. It follows from Eqn (4.25) as well that

${\dot{m}}_{0} δ_{L} \sim \frac{λ}{c_{p}}$ ${\dot{m}}_{0} δ_{L} \sim \frac{λ}{c_{p}}$

(4.26)

or that

{\dot{m}}_{0} δ_{L}

${\dot{m}}_{0} δ_{L}$

is essentially equal to a constant, and that for most hydrocarbon–air flames in which nitrogen is the major species and the reaction product molar compositions do not vary greatly,

{\dot{m}}_{0} δ_{L}

${\dot{m}}_{0} δ_{L}$

is the same. How these conclusions compare with the results of comprehensive theory calculations will be examined in Section 4.3.3.

The temperature dependence in the flame speed expression is dominated by the exponential in the rate expression for

\dot{ω}

$\dot{ω}$

; thus, it is possible to assume that

$S_{L} \sim {[\exp (- E / R T)]}^{1 / 2}$ $S_{L} \sim {[\exp (- E / R T)]}^{1 / 2}$

(4.27)

The physical reasoning used indicates that most of the reaction and heat release must occur close to the highest temperature if high activation energy Arrhenius kinetics controls the process. Thus, the temperature to be used in the above expression is T_f and one rewrites Eqn (4.27) as

$S_{L} \sim {[\exp (- E / R T_{f})]}^{1 / 2}$ $S_{L} \sim {[\exp (- E / R T_{f})]}^{1 / 2}$

(4.28)

Therefore, the effect of varying the initial temperature is found in the degree to which it alters the flame temperature. Recall that, owing to chemical energy release, a 100° rise in initial temperature results in a rise of flame temperature that is much smaller. These trends due to temperature have been verified experimentally.

4.3.2. Theory of Zeldovich, Frank–Kamenetskii, and Semenov

As discussed in the previous section, the Russian investigators Zeldovich, Frank–Kamenetskii, and Semenov derived an expression for the laminar flame speed by an important extension of the simplified Mallard–Le Chatelier approach. Their basic equation included diffusion of species as well as heat. Since their initial insight was that flame propagation was fundamentally a thermal mechanism, they were not concerned with the diffusion of radicals and its effect on the reaction rate. They were concerned with the energy transported by the diffusion of species.

As in the Mallard–Le Chatelier approach, an ignition temperature arises in this development, but it is used only as a mathematical convenience for computation. Because the chemical reaction rate is an exponential function of temperature according to the Arrhenius equation, Semenov assumed that the ignition temperature, above which nearly all reaction occurs, is near the flame temperature. With this assumption, the ignition temperature can be eliminated in the mathematical development. Since the energy equation is the one to be solved in this approach, the assumption is physically correct. As described in the previous section for hydrocarbon flames, most of the energy release is due to CO oxidation, which takes place late in the flame where many hydroxyl radicals are available.

For the initial development, although these restrictions are partially removed in further developments, two other important assumptions are made. The assumptions are that the c_p and λ are constant and that

$(λ / c_{p}) = ρ D$ $(λ / c_{p}) = ρ D$

where D is the mass diffusivity. This assumption is essentially that

$α = D$ $α = D$

Simple kinetic theory of gases predicts

$α = D = ν$ $α = D = ν$

where ν is kinematic viscosity (momentum diffusivity). The ratios of these three diffusivities give some of the familiar dimensionless similarity parameters,

$\Pr = ν / α, Sc = ν / D, Le = α / D$ $\Pr = ν / α, Sc = ν / D, Le = α / D$

where Pr, Sc, and Le are the Prandtl, Schmidt, and Lewis numbers, respectively. The Prandtl number is the ratio of momentum to thermal diffusion, the Schmidt number is momentum to mass diffusion, and the Lewis number is thermal to mass diffusion. Elementary kinetic theory of gases then predicts as a first approximation

$\Pr = Sc = Le = 1$ $\Pr = Sc = Le = 1$

With this approximation, one finds

$(λ / c_{p}) = ρ D \neq f (p)$ $(λ / c_{p}) = ρ D \neq f (p)$

that is, neither (λ/c_p) nor ρD is a function of pressure.

Figure 4.5 Balances across a differential element in a thermal wave describing a laminar flame.

Consider the thermal wave given in Figure 4.4. If a differential control volume is taken within this one-dimensional wave, and the variations as given in the figure are in the x direction, the thermal and mass balances are as shown in Figure 4.5. In Figure 4.5, a is the mass of reactant per cubic centimeter,

\dot{ω}

$\dot{ω}$

is the rate of reaction, Q is the heat of reaction per unit mass, and ρ is the total density. Note that a/ρ is the mass fraction of reactant a, Y_a. Since the problem is a steady one, there is no accumulation of species or heat with respect to time, and the balance of the energy terms and the species terms must each be equal to zero.

The net rate of mass convecting into the volume AΔx (where A is the area usually taken as unity) is

$\dot{m} [(\frac{a}{ρ}) + \frac{d (a / ρ)}{d x} Δ x] A - \dot{m} (\frac{a}{ρ}) A = \dot{m} \frac{d (a / ρ)}{d x} A Δ x$ $\dot{m} [(\frac{a}{ρ}) + \frac{d (a / ρ)}{d x} Δ x] A - \dot{m} (\frac{a}{ρ}) A = \dot{m} \frac{d (a / ρ)}{d x} A Δ x$

(4.29)

For this one-dimensional configuration

\dot{m} = ρ_{0} S_{L}

$\dot{m} = ρ_{0} S_{L}$

. The net rate of mass diffusing into the volume is

$- \frac{d}{d x} [ρ D (\frac{a}{ρ} + \frac{d (a / ρ)}{d x} Δ x)] A - (- ρ D \frac{d (a / ρ)}{d x}) A = - (ρ D) \frac{d^{2} (a / ρ)}{d x^{2}} A Δ x$ $- \frac{d}{d x} [ρ D (\frac{a}{ρ} + \frac{d (a / ρ)}{d x} Δ x)] A - (- ρ D \frac{d (a / ρ)}{d x}) A = - (ρ D) \frac{d^{2} (a / ρ)}{d x^{2}} A Δ x$

(4.30)

The rate at which mass is reacting (i.e., being converted from reactants to products) in the volume is

$\dot{ω} A Δ x$ $\dot{ω} A Δ x$

and it is to be noted that

\dot{ω}

$\dot{ω}$

is a negative quantity. Thus, the continuity equation for the reactant is

$\begin{matrix} - (ρ D) \frac{d^{2} (a / ρ)}{d x^{2}} \\ (diffusion term) \end{matrix} + \begin{matrix} \dot{m} \frac{d (a / ρ)}{d x} + \\ (convective term) \end{matrix} \begin{matrix} \dot{ω} = 0 \\ (generation term) \end{matrix}$ $\begin{matrix} - (ρ D) \frac{d^{2} (a / ρ)}{d x^{2}} \\ (diffusion term) \end{matrix} + \begin{matrix} \dot{m} \frac{d (a / ρ)}{d x} + \\ (convective term) \end{matrix} \begin{matrix} \dot{ω} = 0 \\ (generation term) \end{matrix}$

(4.31)

The energy equation is determined similarly and is

$- λ \frac{d^{2} T}{d x^{2}} + \dot{m} c_{p} \frac{d T}{d x} - \dot{ω} Q = 0$ $- λ \frac{d^{2} T}{d x^{2}} + \dot{m} c_{p} \frac{d T}{d x} - \dot{ω} Q = 0$

(4.32)

Because

\dot{ω}

$\dot{ω}$

is negative, and the overall term must be positive since there is heat release, the third term has a negative sign. The state equation is written as

$(ρ / ρ_{0}) = (T_{0} / T)$ $(ρ / ρ_{0}) = (T_{0} / T)$

New variables are defined as

$\begin{matrix} \tilde{T} = \frac{c_{p} (T - T_{0})}{Q} \\ \tilde{a} = (a_{0} / ρ_{0}) - (a / ρ) \end{matrix}$ $\begin{matrix} \tilde{T} = \frac{c_{p} (T - T_{0})}{Q} \\ \tilde{a} = (a_{0} / ρ_{0}) - (a / ρ) \end{matrix}$

where the subscript 0 designates initial conditions. Substituting the new variables in Eqns (4.31) and (4.32), one obtains two new equations:

$ρ D \frac{d^{2} \tilde{a}}{d x^{2}} - \dot{m} \frac{d \tilde{a}}{d x} + \dot{ω} = 0$ $ρ D \frac{d^{2} \tilde{a}}{d x^{2}} - \dot{m} \frac{d \tilde{a}}{d x} + \dot{ω} = 0$

(4.33)

$\frac{λ}{c_{p}} \frac{d^{2} \tilde{T}}{d x^{2}} - \dot{m} \frac{d \tilde{T}}{d x} + \dot{ω} = 0$ $\frac{λ}{c_{p}} \frac{d^{2} \tilde{T}}{d x^{2}} - \dot{m} \frac{d \tilde{T}}{d x} + \dot{ω} = 0$

(4.34)

The boundary conditions for these equations are

$\begin{matrix} x = - \infty, & \tilde{a} = 0, & \tilde{T} = 0 \\ x = + \infty, & \tilde{a} = a_{0} / ρ_{0}, & \tilde{T} = [c_{p} (T_{f} - T_{0})] / Q \end{matrix}$ $\begin{matrix} x = - \infty, & \tilde{a} = 0, & \tilde{T} = 0 \\ x = + \infty, & \tilde{a} = a_{0} / ρ_{0}, & \tilde{T} = [c_{p} (T_{f} - T_{0})] / Q \end{matrix}$

(4.35)

where T_f is the final or flame temperature. For the condition ρD = (λ/c_p), Eqns (4.33) and (4.34) are identical in form. If the equations and boundary conditions for

\tilde{a}

$\tilde{a}$

and

\tilde{T}

$\tilde{T}$

coincide—that is, if

\tilde{a} = \tilde{T}

$\tilde{a} = \tilde{T}$

over the entire interval, then

$c_{p} T_{0} + (a_{0} Q / ρ_{0}) = c_{p} T_{f} = c_{p} T + (a Q / ρ)$ $c_{p} T_{0} + (a_{0} Q / ρ_{0}) = c_{p} T_{f} = c_{p} T + (a Q / ρ)$

(4.36)

The meaning of Eqn (4.36) is that the sum of the thermal and chemical energies per unit mass of the mixture is constant in the combustion zone; that is, the relation between the temperature and the composition of the gas mixture is the same as that for the adiabatic behavior of the reaction at constant pressure.

Thus, the variable defined in Eqn (4.36) can be used to develop a new equation in the same manner as Eqn (4.31), and the problem reduces to the solution of only one differential equation. Indeed, either Eqn (4.31) or (4.32) can be solved; however, Semenov chose to work with the energy equation.

In the first approach it is assumed as well that the reaction proceeds by zero order. Since the rate term

\dot{ω}

$\dot{ω}$

is not a function of concentration, the continuity equation is not required so we can deal with the more convenient energy equation. Semenov, like Mallard and Le Chatelier, examined the thermal wave as if it were made up of two parts. The unburned gas part is a zone of no chemical reaction, and the reaction part is the zone in which the reaction and diffusion terms dominate and the convective term can be ignored. Thus, in the first zone (I), the energy equation reduces to

$\frac{d^{2} T}{d x^{2}} - \frac{\dot{m} c_{p}}{λ} \frac{d T}{d x} = 0$ $\frac{d^{2} T}{d x^{2}} - \frac{\dot{m} c_{p}}{λ} \frac{d T}{d x} = 0$

(4.37)

with the boundary conditions

$x = - \infty, T = T_{0}; x = 0, T = T_{i}$ $x = - \infty, T = T_{0}; x = 0, T = T_{i}$

(4.38)

It is apparent from the latter boundary condition that the coordinate system is so chosen that T_i is at the origin. The reaction zone extends a small distance δ, so that in the reaction zone (II) the energy equation is written as

$\frac{d^{2} T}{d x^{2}} + \frac{\dot{ω} Q}{λ} = 0$ $\frac{d^{2} T}{d x^{2}} + \frac{\dot{ω} Q}{λ} = 0$

(4.39)

with the boundary conditions

$x = 0, T = T_{i}; x = δ, T = T_{f}$ $x = 0, T = T_{i}; x = δ, T = T_{f}$

The added condition, which permits the determination of the solution (eigenvalue), is the requirement of the continuity of heat flow at the interface of the two zones:

$λ {(\frac{d T}{d x})}_{x = 0, I} = λ {(\frac{d T}{d x})}_{x = 0, II}$ $λ {(\frac{d T}{d x})}_{x = 0, I} = λ {(\frac{d T}{d x})}_{x = 0, II}$

(4.40)

The solution to the problem is obtained by initially considering Eqn (4.39). First, recall that

$\frac{d}{d x} {(\frac{d T}{d x})}^{2} = 2 (\frac{d T}{d x}) \frac{d^{2} T}{d x^{2}}$ $\frac{d}{d x} {(\frac{d T}{d x})}^{2} = 2 (\frac{d T}{d x}) \frac{d^{2} T}{d x^{2}}$

(4.41)

Now, Eqn (4.39) is multiplied by 2 (dT/dx) to obtain

$2 (\frac{d T}{d x}) \frac{d^{2} T}{d x^{2}} = - 2 \frac{\dot{ω} Q}{λ} (\frac{d T}{d x})$ $2 (\frac{d T}{d x}) \frac{d^{2} T}{d x^{2}} = - 2 \frac{\dot{ω} Q}{λ} (\frac{d T}{d x})$

(4.42)

$\frac{d}{d x} {(\frac{d T}{d x})}^{2} = - 2 \frac{\dot{ω} Q}{λ} (\frac{d T}{d x})$ $\frac{d}{d x} {(\frac{d T}{d x})}^{2} = - 2 \frac{\dot{ω} Q}{λ} (\frac{d T}{d x})$

(4.43)

Integrating Eqn (4.43), one obtains

$- {(\frac{d T}{d x})}_{x = 0}^{2} = - 2 \frac{Q}{λ} \int_{T_{i}}^{T_{f}} \dot{ω} d T$ $- {(\frac{d T}{d x})}_{x = 0}^{2} = - 2 \frac{Q}{λ} \int_{T_{i}}^{T_{f}} \dot{ω} d T$

(4.44)

since (dT/dx)², evaluated at x = δ or T = T_f, is equal to zero. But from Eqn (4.37), one has

$\frac{d}{d x} (\frac{d T}{d x}) = \frac{\dot{m} c_{p}}{λ} (\frac{d T}{d x})$ $\frac{d}{d x} (\frac{d T}{d x}) = \frac{\dot{m} c_{p}}{λ} (\frac{d T}{d x})$

(4.45)

Integrating Eqn (4.45), one gets

$d T / d x = (\dot{m} c_{p} / λ) T + const$ $d T / d x = (\dot{m} c_{p} / λ) T + const$

Since at x = −∞, T = T₀ and (dT/dx) = 0

$const = - (\dot{m} c_{p} / λ) T_{0}$ $const = - (\dot{m} c_{p} / λ) T_{0}$

(4.46)

and

$d T / d x = [\dot{m} c_{p} (T - T_{0})] / λ$ $d T / d x = [\dot{m} c_{p} (T - T_{0})] / λ$

(4.47)

Evaluating the expression at x = 0 where T = T_i, one obtains

${(d T / d x)}_{x = 0} = \dot{m} c_{p} (T_{i} - T_{0}) / λ$ ${(d T / d x)}_{x = 0} = \dot{m} c_{p} (T_{i} - T_{0}) / λ$

(4.48)

The continuity of heat flux permits this expression to be combined with Eqn (4.44) to obtain

$\frac{\dot{m} c_{p} (T_{i} - T_{0})}{λ} = {(\frac{2 Q}{λ} \int_{T_{i}}^{T_{f}} \dot{ω} d T)}^{1 / 2}$ $\frac{\dot{m} c_{p} (T_{i} - T_{0})}{λ} = {(\frac{2 Q}{λ} \int_{T_{i}}^{T_{f}} \dot{ω} d T)}^{1 / 2}$

Since Arrhenius kinetics dominate, it is apparent that T_i is very close to T_f, so the last expression is rewritten as

$\frac{\dot{m} c_{p} (T_{f} - T_{0})}{λ} = {(\frac{2 Q}{λ} \int_{T_{i}}^{T_{f}} \dot{ω} d T)}^{1 / 2}$ $\frac{\dot{m} c_{p} (T_{f} - T_{0})}{λ} = {(\frac{2 Q}{λ} \int_{T_{i}}^{T_{f}} \dot{ω} d T)}^{1 / 2}$

(4.49)

For

\dot{m} = S_{L} ρ_{0}

$\dot{m} = S_{L} ρ_{0}$

and (a₀/ρ₀)Q taken equal to c_p(T_f − T₀) (from Eqn (4.36)), one obtains

$S_{L} = [2 (\frac{λ}{ρ c_{p}}) \frac{I}{(T_{f} - T_{0})}]$ $S_{L} = [2 (\frac{λ}{ρ c_{p}}) \frac{I}{(T_{f} - T_{0})}]$

(4.50)

where

$I = \frac{1}{a_{0}} \int_{T_{i}}^{T_{f}} \dot{ω} d T$ $I = \frac{1}{a_{0}} \int_{T_{i}}^{T_{f}} \dot{ω} d T$

(4.51)

and

\dot{ω}

$\dot{ω}$

is a function of T and not of concentration for a zero-order reaction. Thus, it may be expressed as

$\dot{ω} = Z^{'} e^{- E / R T}$ $\dot{ω} = Z^{'} e^{- E / R T}$

(4.52)

where Z′ is the pre-exponential term in the Arrhenius expression.

For sufficiently large energy of activation such as that for hydrocarbon–oxygen mixtures where E is of the order of 160 kJ/mol, (E/RT) > 1. Thus, most of the energy release will be near the flame temperature, T_i will be very near the flame temperature, and zone II will be a very narrow region. Consequently, it is possible to define a new variable σ such that

$σ = (T_{f} - T)$ $σ = (T_{f} - T)$

(4.53)

The values of σ will vary from

$σ_{i} = (T_{f} - T_{i})$ $σ_{i} = (T_{f} - T_{i})$

(4.54)

to zero. Since

$σ < T_{f}$ $σ < T_{f}$

then

$\begin{matrix} (E / R T) = [E / R (T_{f} - σ)] = [E / R T_{f} (1 - σ / T_{f})] \\ ≃ (E / R T_{f}) [1 + (σ / T_{f})] = (E / R T_{f}) + (E σ / R T_{f}^{2}) \end{matrix}$ $\begin{matrix} (E / R T) = [E / R (T_{f} - σ)] = [E / R T_{f} (1 - σ / T_{f})] \\ ≃ (E / R T_{f}) [1 + (σ / T_{f})] = (E / R T_{f}) + (E σ / R T_{f}^{2}) \end{matrix}$

Thus, the integral I becomes

$I = \frac{Z^{'} e^{- E / R T_{f}}}{a_{0}} \int_{T_{i}}^{T_{f}} e^{- E σ / R T_{f}^{2}} d T = \frac{- Z^{'} e^{- E / R T_{f}}}{a_{0}} \int_{σ_{i}}^{0} e^{- E σ / R T_{f}^{2}} d σ$ $I = \frac{Z^{'} e^{- E / R T_{f}}}{a_{0}} \int_{T_{i}}^{T_{f}} e^{- E σ / R T_{f}^{2}} d T = \frac{- Z^{'} e^{- E / R T_{f}}}{a_{0}} \int_{σ_{i}}^{0} e^{- E σ / R T_{f}^{2}} d σ$

(4.55)

Defining still another variable ξ as

$ξ = E σ / R T_{f}^{2}$ $ξ = E σ / R T_{f}^{2}$

(4.56)

the integral becomes

$I = \frac{Z^{'} e^{- E / R T_{f}}}{a_{0}} [\int_{0}^{ξ_{i}} e^{- ξ} d ξ] \frac{R T_{f}^{2}}{E}$ $I = \frac{Z^{'} e^{- E / R T_{f}}}{a_{0}} [\int_{0}^{ξ_{i}} e^{- ξ} d ξ] \frac{R T_{f}^{2}}{E}$

(4.57)

With sufficient accuracy one may write

$j = \int_{0}^{ξ_{i}} e^{- ξ} d ξ = (1 - e^{- ξ_{i}}) ≅ 1$ $j = \int_{0}^{ξ_{i}} e^{- ξ} d ξ = (1 - e^{- ξ_{i}}) ≅ 1$

(4.58)

since (E/RT_f) > 1 and (σ_i/T_f) ≅ 0.25. Thus,

$I = (\frac{Z^{'}}{a_{0}}) (\frac{R T_{f}^{2}}{E}) e^{- E / R T_{f}}$ $I = (\frac{Z^{'}}{a_{0}}) (\frac{R T_{f}^{2}}{E}) e^{- E / R T_{f}}$

(4.59)

and

$S_{L} = {[\frac{2}{a_{0}} (\frac{λ}{ρ_{0} c_{p}}) (Z^{'} e^{- E / R T_{f}}) (\frac{R T_{f}^{2}}{E (T_{f} - T_{0})})]}^{1 / 2}$ $S_{L} = {[\frac{2}{a_{0}} (\frac{λ}{ρ_{0} c_{p}}) (Z^{'} e^{- E / R T_{f}}) (\frac{R T_{f}^{2}}{E (T_{f} - T_{0})})]}^{1 / 2}$

(4.60)

In the preceding development, it was assumed that the number of moles did not vary during reaction. This restriction can be removed to allow the number to change in the ratio (n_r/n_p), which is the number of moles of reactant to product. Furthermore, the Lewis number equal to one restriction can be removed to allow

$(λ / c_{p}) / ρ D = A / B$ $(λ / c_{p}) / ρ D = A / B$

where A and B are constants. With these restrictions removed, the result for a first-order reaction becomes

$S_{L} = {\frac{2 λ_{f} c_{p f} Z^{'}}{ρ_{0} {\bar{c}}_{p}^{2}} (\frac{T_{0}}{T_{f}}) (\frac{n_{r}}{n_{p}}) (\frac{A}{B}) {(\frac{R T_{f}^{2}}{E})}^{2} \frac{e^{- E / R T_{f}}}{{(T_{f} - T_{0})}^{2}}}^{1 / 2}$ $S_{L} = {\frac{2 λ_{f} c_{p f} Z^{'}}{ρ_{0} {\bar{c}}_{p}^{2}} (\frac{T_{0}}{T_{f}}) (\frac{n_{r}}{n_{p}}) (\frac{A}{B}) {(\frac{R T_{f}^{2}}{E})}^{2} \frac{e^{- E / R T_{f}}}{{(T_{f} - T_{0})}^{2}}}^{1 / 2}$

(4.61)

and for a second-order reaction

$S_{L} = {\frac{2 λ c_{p f}^{2} Z^{'} a_{0}}{ρ_{0} {({\bar{c}}_{p})}^{3}} {(\frac{T_{0}}{T_{f}})}^{2} (\frac{n_{r}}{n_{p}}) {(\frac{A}{B})}^{2} {(\frac{R T_{f}^{2}}{E})}^{3} \frac{e^{- E / R T_{f}}}{{(T_{f} - T_{0})}^{3}}}^{1 / 2}$ $S_{L} = {\frac{2 λ c_{p f}^{2} Z^{'} a_{0}}{ρ_{0} {({\bar{c}}_{p})}^{3}} {(\frac{T_{0}}{T_{f}})}^{2} (\frac{n_{r}}{n_{p}}) {(\frac{A}{B})}^{2} {(\frac{R T_{f}^{2}}{E})}^{3} \frac{e^{- E / R T_{f}}}{{(T_{f} - T_{0})}^{3}}}^{1 / 2}$

(4.62)

where c_pf is the specific heat evaluated at T_f and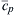

{\bar{c}}_{p}

${\bar{c}}_{p}$

is the average specific heat between T₀ and T_f.

Notice that a₀ and ρ₀ are both proportional to pressure and S_L is independent of pressure. Furthermore, this complex development shows that

$S_{L} \sim {(\frac{λ c_{p f}^{2}}{ρ_{0} {({\bar{c}}_{p})}^{3}} a_{0} Z^{'} e^{- E / R T_{f}})}^{1 / 2}, S_{L} \sim {(\frac{λ}{ρ_{0} c_{p}} R R)}^{1 / 2} \sim {(α R R)}^{1 / 2}$ $S_{L} \sim {(\frac{λ c_{p f}^{2}}{ρ_{0} {({\bar{c}}_{p})}^{3}} a_{0} Z^{'} e^{- E / R T_{f}})}^{1 / 2}, S_{L} \sim {(\frac{λ}{ρ_{0} c_{p}} R R)}^{1 / 2} \sim {(α R R)}^{1 / 2}$

(4.63)

as was obtained from the simple Mallard–Le Chatelier approach.

4.3.3. Comprehensive Theory and Laminar Flame Structure Analysis

To determine the laminar flame speed and flame structure, it is now possible to solve by computational techniques the steady-state comprehensive mass, species, and energy conservation equations with a complete reaction mechanism for the fuel–oxidizer system which specifies the heat release. The numerical code for this simulation of a freely propagating, one-dimensional, adiabatic premixed flame is based on the scheme of Kee et al. [15]. The code uses a hybrid time-integration/Newton-iteration technique to solve the equations. The mass burning rate of the flame is calculated as an eigenvalue of the problem and, since the unburned gas mixture density is known, the flame speed S_L is determined

(\dot{m} = ρ_{0} S_{L})

$(\dot{m} = ρ_{0} S_{L})$

. In addition, the code permits one to examine the complete flame structure and the sensitivities of all reaction rates on the temperature and species profiles as well as on the mass burning rate. Generally, two preprocessors are used in conjunction with the freely propagating flame code. The first, CHEMKIN, is used to evaluate the thermodynamic properties of the reacting mixture and to process an established chemical reaction mechanism of the particular fuel–oxidizer system [16]. The second is a molecular property package which provides the transport properties of the mixture [17] (see Appendix I).

To evaluate the flame structure of characteristic fuels, this procedure was applied to propane–, methane–, and hydrogen–air flames at the stoichiometric equivalence ratio and unburned gas conditions of 298 K and 1 atm. The fuels were chosen because of their different kinetic characteristics. Propane is characteristic of most of the higher-order hydrocarbons. As discussed in the previous chapter, methane is unique with respect to hydrocarbons, and hydrogen is a non-hydrocarbon that exhibits the largest mass diffusivity. Table 4.1 reports the calculated values of the mass burning rate and laminar flame speed, and Figures 4.6–4.12 report the species, temperature, and heat release rate distributions. These figures and Table 4.1 reveal much about the flame structure and confirm much of what was described in this and preceding chapters. The δ_L reported in Table 4.1 was estimated by considering the spatial distance of the first perceptible rise of the temperature or reactant decay in the figures and the extrapolation of the

\dot{q}

$\dot{q}$

curve decay branch to the axis. This procedure eliminates the gradual curvature of the decay branch near the point where all fuel elements are consumed and which is due to radical recombination. Since for hydrocarbons one would expect (λ/c_p) to be approximately the same, the values of

{\dot{m}}_{0} δ_{L}

${\dot{m}}_{0} δ_{L}$

for CH₄ and C₃H₈ in Table 4.1 should be close, as indeed they are. Since the thermal conductivity of H₂ is much larger than that of gaseous hydrocarbons, it is not surprising that its value of

{\dot{m}}_{0} δ_{L}

${\dot{m}}_{0} δ_{L}$

is larger than those for CH₄ and C₃H₈. What the approximation

{\dot{m}}_{0} δ_{L} \sim (λ / c_{p})

${\dot{m}}_{0} δ_{L} \sim (λ / c_{p})$

truly states is that

{\dot{m}}_{0} δ_{L} / (λ / c_{p})

${\dot{m}}_{0} δ_{L} / (λ / c_{p})$

is of order 1. This order simply arises from the fact that if the thermal equation in the flame speed development is non-dimensionalized with δ_L and S_L as the critical dimension and velocity, then

{\dot{m}}_{0} δ_{L} / (λ / c_{p})

${\dot{m}}_{0} δ_{L} / (λ / c_{p})$

is the Peclet number (Pe) before the convection term in this equation. This point can be readily seen from

Table 4.1

Flame Properties at ϕ = 1^a

Fuel/Air	S_L (cm/s)	${\dot{m}}_{0} = ρ S_{L}$ ${\dot{m}}_{0} = ρ S_{L}$ (g/cm² s)	$δ_{L}$ $δ_{L}$ (cm (est.))	${\dot{m}}_{0} δ_{L}$ ${\dot{m}}_{0} δ_{L}$ (g/cm s)	(m˙₀δ_L)/(λ/c_p)₀
H₂	219.7	0.187	0.050 (Figure 4.11)	0.0093	0.73
CH₄	36.2	0.041	0.085 (Figure 4.9)	0.0035	1.59
C₃H₈	46.3	0.055	0.057 (Figure 4.6)	0.0031	1.41

Figure 4.6 Composition, temperature, and heat release rate profiles for a stoichiometric C₃H₈–air laminar flame at 1 atm and T₀ = 298 K.

Figure 4.7 Reaction intermediates for Figure 4.6.

Figure 4.8 Radical distribution profiles for Figure 4.6.

Figure 4.9 Composition, temperature, and heat release rate profiles for a stoichiometric CH₄–air laminar flames at 1 atm and T₀ = 298 K.

Figure 4.10 Radical distribution profiles for Figure 4.9.

Figure 4.11 Composition, temperature, and heat release rate profiles for a stoichiometric H₂–air laminar flame at 1 atm and T₀ = 298 K.

Figure 4.12 Radical distribution profiles for Figure 4.11.

$\frac{{\dot{m}}_{0} δ_{L}}{(λ / c_{p})} = \frac{ρ_{0} δ_{L} S_{L}}{(λ / c_{p})} = \frac{S_{L} δ_{L}}{α_{0}} = Pe$ $\frac{{\dot{m}}_{0} δ_{L}}{(λ / c_{p})} = \frac{ρ_{0} δ_{L} S_{L}}{(λ / c_{p})} = \frac{S_{L} δ_{L}}{α_{0}} = Pe$

Since

{\dot{m}}_{0} = ρ_{0} S_{L}

${\dot{m}}_{0} = ρ_{0} S_{L}$

, the term (λ/c_p) above and in Table 4.1 is evaluated at the unburned gas condition. Considering that δ_L has been estimated from graphs, the value for all fuels in the last column of Table 4.1 can certainly be considered of order 1.

Figures 4.6–4.8 are the results for the stoichiometric propane–air flame. Figure 4.6 reports the variance of the major species, temperature, and heat release; Figure 4.7 reports the major stable propane fragment distribution due to the proceeding reactions; and Figure 4.8 shows the radical and formaldehyde distributions—all as a function of a spatial distance through the flame wave. As stated, the total wave thickness is chosen from the point at which one of the reactant mole fractions begins to decay to the point at which the heat release rate begins to taper off sharply. Since the point of initial reactant decay corresponds closely to the initial perceptive rise in temperature, the initial thermoneutral period is short. The heat release rate curve would ordinarily drop to zero sharply, except that the recombination of the radicals in the burned gas zone contributes some energy. The choice of the position that separates the preheat zone and the reaction zone has been made to account for the slight exothermicity of the fuel attack reactions by radicals that have diffused into the preheat zone, and the reaction of the resulting species to form water. Note that water and hydrogen exist in the preheat zone. This choice of operation is then made at the point where the heat release rate curve begins to rise sharply. At this point, as well, there is noticeable CO. This certainly establishes the lack of a sharp separation between the preheat and reaction zones discussed earlier in this chapter and indicates that in the case of propane–air flames the zones overlap. On the basis just described, the thickness of the complete propane–air flame wave is about 0.6 mm, and the preheat and reaction zones are about 0.3 mm each. Thus, although maximum heat release rate occurs near the maximum flame temperature (if it were not for the radicals recombining), the ignition temperature in the sense of Mallard–Le Chatelier and Zeldovich–Frank–Kamenetskii–Semenov is not close to the flame temperature.

Consistent with the general conditions that occur in flames, the HO₂ formed by H atom diffusion upstream maximizes just before the reaction zone, which in turn leads to the formation of H₂O₂ and its subsequent decomposition to OH radicals. This point is in the 900–1000 K range known to be the thermal condition for H₂O₂ decomposition. As would be expected, this point corresponds to the rapid decline of the fuel mole fraction and the onset of radical chain branching. Thus, the rapid rise of the radical mole fractions and the formation of the olefins and methane intermediates occur at this point as well (see Figures 4.7 and 4.8). The peak of the intermediates is followed by those of formaldehyde, CO, and CO₂ in the order described from flow reactor results.

Propane disappears well before the end of the reaction zone to form as major intermediates ethene, propene, and methane in magnitudes that the β-scission rule and the type and number of C–H bonds would have predicted. Likewise, owing to the greater availability of OH radicals after the fuel disappearance, the CO₂ concentration begins to rise sharply as the fuel concentration decays.

It is not surprising that the depth of the methane–air flame wave is thicker than that of propane–air (Figure 4.9). Establishing the same criteria for estimating this thickness, the methane–air wave thickness appears to be about 0.9 mm.

The thermal thickness is estimated to be 0.5 mm, and the reaction thickness is about 0.4 mm. Much of what was described for the propane–air flame holds for methane–air except as established from the knowledge of methane–air oxidation kinetics; the methane persists through the whole reaction zone and there is a greater overlap of the preheat and reaction zones. Figure 4.10 reveals that at the chosen boundary between the two zones, the methyl radical mole fraction begins to rise sharply. The formaldehyde curve reveals the relatively rapid early conversion of these forms of methyl radicals; that is, as the peroxy route produces ample OH, the methane is more rapidly converted to methyl radical while simultaneously the methyl is converted to formaldehyde. Again, initially, the large mole fraction increases of OH, H, and O are due to H₂–O₂ chain branching at the temperature corresponding to this boundary point. In essence, this point is where explosive reaction occurs, and the radical pool is more than sufficient to convert the stable reactants and intermediates to products.

Figure 4.13 Heat release rate and temperature profiles for a stoichiometric CH₄–air laminar flame at various pressures and T₀ = 298 K.

If the same criteria are applied to the analysis of the H₂–air results in Figures 4.11 and 4.12, some initially surprising conclusions are reached. At best, it can be concluded that the flame thickness is approximately 0.5 mm. At most, if any preheat zone exists, it is only 0.1 mm. In essence, then, because of the formation of large H atom concentrations, there is extensive upstream H atom diffusion that causes the sharp rise in HO₂. This HO₂ reacts with the H₂ fuel to form H atoms and H₂O₂, which immediately dissociates into OH radicals. Furthermore, even at these low temperatures, the OH reacts with the H₂ to form water and an abundance of H atoms. This reaction is about 50 kJ exothermic. What appears as a rise in the O₂ is indeed only a rise in mole fraction and not in mass.

Figure 4.13 reports the results of varying the pressure from 0.5 to 8 atm on the structure of stoichiometric methane–air flames, and Table 4.2 gives the corresponding flame speeds and mass burning rates. Note from Table 4.2 that as the pressure increases, the flame speed decreases and the mass burning rate increases for the reasons discussed in Section 4.3.1. The fact that the temperature profiles in Figure 4.13 steepen as the pressure rises and that the flame speed results in Table 4.2 decline with pressure would at first appear counterintuitive in light of the simple thermal theories. However, the thermal diffusivity is also pressure-dependent and is inversely proportional to the pressure. Thus, the thermal diffusivity effect overrides the effect of pressure on the reaction rate and the energy release rate, which affects the temperature distribution. The mass burning rate increases with pressure, although for a few particular reacting systems either the flame speed or the mass burning rate might not follow the trends shown. However, for most hydrocarbon–air systems the trends described would hold.

Table 4.2

Flame Properties as a Function of Pressure^a

P (atm)	S_L (cm/s)	${\dot{m}}_{0} = ρ S_{L}$ ${\dot{m}}_{0} = ρ S_{L}$ (g/cm² s)	$δ_{L}$ $δ_{L}$ (cm (est.))^b	${\dot{m}}_{0} δ_{L}$ ${\dot{m}}_{0} δ_{L}$ (g/cm s)	(m˙₀δ_L)/(λ/c_p)₀
0.25	54.51	0.015	0.250	0.0038	1.73
1.00	36.21	0.041	0.085	0.0035	1.59
8.00	18.15	0.163	0.022	0.0036	1.64

As discussed for Table 4.1 and considering that (λ/c_p) ≠ f (P), it is not surprising that

{\dot{m}}_{0} δ_{L}

${\dot{m}}_{0} δ_{L}$

and

({\dot{m}}_{0} δ_{L}) / {(λ / c_{p})}_{0}

$({\dot{m}}_{0} δ_{L}) / {(λ / c_{p})}_{0}$

in Table 4.2 essentially do not vary with pressure and remain of order 1.

4.3.4. Laminar Flame and Energy Equation

An important point about laminar flame propagation—one that has not previously been discussed—is worth stressing: It has become common to accept that reaction rate phenomena dominate in premixed homogeneous combustible gaseous mixtures and diffusion phenomena dominate in initially unmixed fuel–oxidizer systems. (The subject of diffusion flames will be discussed in Chapter 6.) In the case of laminar flames, and indeed in most aspects of turbulent flame propagation, it should be emphasized that it is the diffusion of heat (and mass) that causes the flame to propagate; that is, flame propagation is a diffusional mechanism. The reaction rate determines the thickness of the reaction zone and, thus, the temperature gradient. The temperature effect is indeed a strong one, but flame propagation is still attributable to the diffusion of heat and mass. The expression S_L ∼ (αRR)^1/2 says it well—the propagation rate is proportional to the square root of the diffusivity and the reaction rate.

4.3.5. Flame Speed Measurements

For a long time there was no interest in flame speed measurements. Sufficient data and understanding were thought to be at hand. But as lean burn conditions became popular in spark ignition engines, the flame speed of lean limits became important. Thus, interest has been rekindled in measurement techniques.

Flame velocity has been defined as the velocity at which the unburned gases move through the combustion wave in a direction normal to the wave surface. If, in an infinite plane flame, the flame is regarded as stationary and a particular flow tube of gas is considered, the area of the flame enclosed by the tube does not depend on how the term “flame surface or wave surface” in which the area is measured is defined. The areas of all parallel surfaces are the same, whatever property (particularly temperature) is chosen to define the surface; and these areas are all equal to each other and to that of the inner surface of the luminous part of the flame. The definition is more difficult in any other geometric system. Consider, for example, an experiment in which gas is supplied at the center of a sphere and flows radially outward in a laminar manner to a stationary spherical flame. The inward movement of the flame is balanced by the outward flow of gas. The experiment takes place in an infinite volume at constant pressure. The area of the surface of the wave will depend on where the surface is located. The area of the sphere for which T = 500 °C will be less than that of one for which T = 1500 °C. So if the burning velocity is defined as the volume of unburned gas consumed per second divided by the surface area of the flame, the result obtained will depend on the particular surface selected. The only quantity that remains constant in this system is the product u_rρ_rA_r, where u_r is the velocity of flow at the radius r, where the surface area is A_r, and the gas density is ρ_r. This product equals

{\dot{m}}_{r}

${\dot{m}}_{r}$

, the mass flowing through the layer at r per unit time, and must be constant for all values of r. Thus, u_r varies with r the distance from the center in the manner shown in Figure 4.14.

It is apparent from Figure 4.14 that it is difficult to select a particular linear flow rate of unburned gas up to the flame and regard this velocity as the burning velocity.

If an attempt is made to define burning velocity strictly for such a system, it is found that no definition free from all possible objections can be formulated. Moreover, it is impossible to construct a definition that will, of necessity, determine the same value as that found in an experiment using a plane flame. The essential difficulties are as follow: (1) Over no range of r values does the linear velocity of the gas have even an approximately constant value; and (2) in this ideal system, the temperature varies continuously from the center of the sphere outward and approaches the flame surface asymptotically as r approaches infinity. So no spherical surface can be considered to have a significance greater than any other.

Figure 4.14 Velocity and temperature variations through non–one-dimensional flame systems.

In Figure 4.14, u_x, the velocity of gas flow at x for a plane flame is plotted on the same scale against x, the space coordinate measured normal to the flame front. It is assumed that over the main part of the rapid temperature rise, u_r and u_x coincide. This correspondence is likely to be true if the curvature of the flame is large compared with the flame thickness. The burning velocity is then, strictly speaking, the value to which u_x approaches asymptotically as x approaches −∞. However, because the temperature of the unburned gas varies exponentially with x, the value of u_x becomes effectively constant only a very short distance from the flame. The value of u_r on the low-temperature side of the spherical flame will not at any point be as small as the limiting value of u_x. In fact, the difference, although not zero, will probably not be negligible for such flames. This value of u_r could be determined using the formula

$u_{r} = \dot{m} / ρ_{r} A_{r}$ $u_{r} = \dot{m} / ρ_{r} A_{r}$

Since the layer of interest is immediately on the unburned side of the flame, ρ_r will be close to ρ_u, the density of the unburned gas, and

\dot{m} / ρ

$\dot{m} / ρ$

will be close to the volume flow rate of unburned gas.

So, to obtain in practice a value for burning velocity close to that for the plane flame, it is necessary to locate and measure an area as far on the unburned side of the flame as possible.

Systems such as Bunsen flames are in many ways more complicated than either the plane case or the spherical case. Before proceeding, consider the methods of observation. The following methods have been most widely used to observe the flame:

1. The luminous part of the flame is observed, and the side of this zone, which is toward the unburned gas, is used for measurement (direct photograph).

2. A shadowgraph picture is taken.

3. A Schlieren picture is taken.

4. An interferometric measurement is made (less common).

Which surface in the flame does each method give? Again, consider the temperature distribution through the flame as given in Figure 4.15. The luminous zone comes late in the flame and thus is generally not satisfactory.

A shadowgraph picture measures the derivative of the density gradient (∂ρ/∂x) or (−1/T²)(∂T/∂x); that is, it evaluates {∂[(−1/T²)(∂T/∂x)]/∂x} = (2/T³)(∂T/∂x)² − (1/T²)(∂²T/∂x²). Shadowgraphs, therefore measure the earliest variational front and do not precisely specify a surface. Actually, it is possible to define two shadowgraph surfaces—one at the unburned side and one on the burned side. The inner cone is much brighter than the outer cone, since the absolute value for the expression above is greater when evaluated at T₀ than at T_f.

Schlieren photography gives simply the density gradient (∂ρ/∂x) or (−1/T²) (∂T/∂x), which has the greatest value about the inflection point of the temperature curve; it also corresponds more closely to the ignition temperature. This surface lies early in the flame, is more readily definable than most images, and is recommended and preferred by many workers. Interferometry, which measures density or temperature directly, is much too sensitive and can be used only on two-dimensional flames. In an exaggerated picture of a Bunsen tube flame, the surfaces would lie as shown in Figure 4.16.

Figure 4.15 Temperature regimes in a laminar flame.

The various experimental configurations used for flame speeds may be classified under the following headings:

1. Conical stationary flames on cylindrical tubes and nozzles

2. Flames in tubes

3. Soap bubble method

4. Constant volume explosion in spherical vessel

5. Flat flame methods

The methods are listed in order of decreasing complexity of flame surface and correspond to an increasing complexity of experimental arrangement. Each has certain advantages that attend its usage.

Figure 4.16 Optical fronts in a Bunsen burner flame.

4.3.5.1. Burner method

In this method, premixed gases flow up a jacketed cylindrical tube long enough to ensure streamline flow at the mouth. The gas burns at the mouth of the tube, and the shape of the Bunsen cone is recorded and measured by various means and in various ways. When shaped nozzles are used instead of long tubes, the flow is uniform instead of parabolic and the cone has straight edges. Because of the complicated flame surface, the different procedures used for measuring the flame cone have led to different results.

The burning velocity is not constant over the cone. The velocity near the tube wall is lower because of cooling by the walls. Thus, there are lower temperatures that lead to lower reaction rates and, consequently, lower flame speeds. The top of the cone is crowded owing to the large energy release; therefore, reaction rates are too high.

It has been found that 30% of the internal portion of the cone gives a constant flame speed when related to the proper velocity vector, thereby giving results comparable with other methods. Actually, if one measures S_L at each point, one will see that it varies along every point for each velocity vector, so it is not really constant. This variation is the major disadvantage of this method.

The earliest procedure of calculating flame speed was to divide the volume flow rate (cm³ s⁻¹) by the area (cm²) of flame cone:

$S_{L} = \frac{Q}{A} (\frac{c m^{3} s^{- 1}}{c m^{2}} = cm s^{- 1})$ $S_{L} = \frac{Q}{A} (\frac{c m^{3} s^{- 1}}{c m^{2}} = cm s^{- 1})$

It is apparent, then, that the choice of cone surface area will give widely different results. Experiments in which fine magnesium oxide particles are dispersed in the gas stream have shown that the flow streamlines remain relatively unaffected until the Schlieren cone, then diverge from the burner axis before reaching the visible cone. These experiments have led many investigators to use the Schlieren cone as the most suitable one for flame speed evaluation.

The shadowgraph cone is used by many experimenters because it is much simpler than the Schlieren techniques. Moreover, because the shadowgraph is on the cooler side, it certainly gives more correct results than the visible cone. However, the flame cone can act as a lens in shadowgraph measurements, causing uncertainties to arise with respect to the proper cone size.

Some investigators have concentrated on the central portion of the cone only, focusing on the volume flow through tube radii corresponding to this portion. The proper choice of cone is of concern here also.

The angle the cone slant makes with the burner axis can also be used to determine S_L (see Figure 4.17). This angle should be measured only at the central portion of the cone. Thus S_L = u_u sin α.

Two of the disadvantages of the burner methods are:

1. Wall effects can never be completely eliminated.

2. A steady source of gas supply is necessary, which is hard to come by for rare or pure gases.

The next three methods to be discussed make use of small amounts of gas.

Figure 4.17 Velocity vectors in a Bunsen cone flame.

4.3.5.2. Cylindrical tube method

In this method, a gas mixture is placed in a horizontal tube opened at one end; then the mixture is ignited at the open end of the tube. The rate of progress of the flame into the unburned gas is the flame speed. The difficulty with this method is that, owing to buoyancy effects, the flame front is curved. Then the question arises as to which flame area to use. The flame area is no longer a geometric image of the tube; if it is hemispherical, S_LA_f = u_mπR². Closer observation also reveals quenching at the wall. Therefore, the unaffected center mixes with an affected peripheral area.

Because a pressure wave is established by the burning (recall that heating causes pressure change), the statement that the gas ahead of the flame is not affected by the flame is incorrect. This pressure wave causes a velocity in the unburned gases, so one must account for this movement. Therefore, since the flame is in a moving gas, this velocity must be subtracted from the measured value. Moreover, friction effects downstream generate a greater pressure wave; therefore, length can have an effect. One can deal with this by capping the end of the tube, drilling a small hole in the cap, and measuring the efflux with a soap solution [18]. The rate of growth of the resultant soap bubble is used to obtain the velocity exiting the tube, and hence the velocity of unburned gas. A restriction at the open end minimizes effects owing to the backflow of the expanding burned gases.

These adjustments permit relatively good values to be obtained, but still there are errors resulting from wall effects and distortion due to buoyancy. This buoyancy effect can be remedied by turning the tube vertically.

4.3.5.3. Soap bubble method

In an effort to eliminate wall effects, two spherical methods were developed. In the one discussed here, the gas mixture is contained in a soap bubble and ignited at the center by a spark so that a spherical flame spreads radially through the mixture. Because the gas is enclosed in a soap film, the pressure remains constant. The growth of the flame front along a radius is followed by some photographic means. Because at any stage of the explosion the burned gas behind the flame occupies a larger volume than it did as unburned gas, the fresh gas into which the flame is burning moves outward. Then,

$S_{L} A ρ_{0} = u_{r} A ρ_{f}$ $S_{L} A ρ_{0} = u_{r} A ρ_{f}$

$(\begin{matrix} amount of material \\ that must go into \\ flame to increase \\ volume \end{matrix}) = velocity observed$ $(\begin{matrix} amount of material \\ that must go into \\ flame to increase \\ volume \end{matrix}) = velocity observed$

$S_{L} = u_{r} (ρ_{f} / ρ_{0})$ $S_{L} = u_{r} (ρ_{f} / ρ_{0})$

The great disadvantage is the large uncertainty in the temperature ratio T₀/T_f necessary to obtain ρ_f/ρ₀. Other disadvantages are the facts that (1) the method can only be used for fast flames to avoid the convective effect of hot gases, and (2) the method cannot work with dry mixtures.

4.3.5.4. Closed spherical bomb method

The bomb method is similar to the bubble method except that the constant volume condition causes a variation in pressure. One must therefore follow the pressure simultaneously with the flame front.

As in the soap bubble method, only fast flames can be used because the adiabatic compression of the unburned gases must be measured to calculate the flame speed. Also, the gas into which the flame is moving is always changing; consequently, both the burning velocity and flame speed vary throughout the explosion. These features make the treatment complicated and, to a considerable extent, uncertain.

The following expression has been derived for the flame speed [19]:

$S_{L} = [1 - \frac{R^{3} - r^{3}}{3 P γ_{u} r^{2}} \frac{d P}{d r}] \frac{d r}{d t}$ $S_{L} = [1 - \frac{R^{3} - r^{3}}{3 P γ_{u} r^{2}} \frac{d P}{d r}] \frac{d r}{d t}$

where R is the sphere radius and r is the radius of spherical flames at any moment. The fact that the second term in the brackets is close to 1 makes it difficult to attain high accuracy.

4.3.5.5. Flat flame burner method

The flat flame burner method is usually attributed to Powling [20]. Because it offers the simplest flame front—one in which the area of shadowgraph, Schlieren, and visible fronts are all the same—it is probably the most accurate.

By placing either a porous metal disk or a series of small tubes (1 mm or less in diameter) at the exit of the larger flow tube, one can create suitable conditions for flat flames. The flame is usually ignited with a high flow rate, and then the flow or composition is adjusted until the flame is flat. Next, the diameter of the flame is measured and the area is divided into the volume flow rate of unburned gas. If the velocity emerging is greater than the flame speed, one obtains a cone owing to the larger flame required. If velocity is too slow, the flame tends to flash back and is quenched. To accurately define the edges of the flame, an inert gas is usually flowed around the burners. By controlling the rate of efflux of burned gases with a grid, a more stable flame is obtained. This experimental apparatus is illustrated in Figure 4.18.

Figure 4.18 Flat flame burner apparatus.

As originally developed by Powling, this method was applicable only to mixtures with low burning velocities of the order of 15 cm/s and less. At higher burning velocities, the flame front positions itself too far from the burner and takes a multiconical form.

Later, however, Spalding and Botha [21] extended the flat flame burner method to higher flame speeds by cooling the plug. The cooling draws the flame front closer to the plug and stabilizes it. Operationally, the procedure is as follows. A flow rate giving a velocity greater than the flame speed is set, and the cooling is controlled until a flat flame is obtained. For a given mixture ratio many cooling rates are used. A plot of flame speed versus cooling rate is made and extrapolated to zero cooling rate (Figure 4.19). At this point the adiabatic flame speed S_L is obtained. This procedure can be used for all mixture ratios within the flammability limits. This procedure is superior to the other methods because the heat that is generated leaks to the porous plug, not to the unburned gases as in the other model. Thus, quenching occurs all along the plug, not just at the walls.

The temperature at which the flame speed is measured is calculated as follows. For the approach gas temperature, one calculates what the initial temperature would have been if there were no heat extraction. Then the velocity of the mixture, which would give the measured mass flow rate at this temperature, is determined. This velocity is S_L at the calculated temperature. Detailed descriptions of various burner systems and techniques are to be found in Ref. [22].

A similar flat flame technique—one that does not require a heat loss correction—is the so-called opposed jet system. This approach to measuring flame speeds was introduced to determine the effect of flame stretch on the measured laminar flame velocity. The concept of stretch was introduced in attempts to understand the effects of turbulence on the mass burning rate of premixed systems. (This subject is considered in more detail in Section 4.6.) The technique uses two opposing jets of the same air–fuel ratio to create an almost planar stagnation plane with two flat flames on both sides of the plane. For the same mixture ratio, stable flames are created for different jet velocities. In each case, the opposing jets have the same exit velocity. The velocity leaving a jet decreases from the jet exit toward the stagnation plane. This velocity gradient is related to the stretch affecting the flames: the larger the gradient, the greater the stretch. Measurements are made for different gradients for a fixed mixture. A plot is then made of the flame velocity as a function of the calculated stress function (velocity gradient), and the values are extrapolated to zero velocity gradient. The extrapolated value is considered to be the flame velocity free from any stretch effects—a value that can be compared to theoretical calculations that do not account for the stretch factor. The same technique is used to evaluate diffusion flames in which one jet contains the fuel and the other the oxidizer. Figures depicting opposed jet systems are shown in Chapter 6. The effect of stretch on laminar premixed flame speeds is generally slight for most fuels in air.

Figure 4.19 Cooling effect in flat flame burner apparatus.

4.3.6. Experimental Results—Physical and Chemical Effects

The Mallard–Le Chatelier development for the laminar flame speed permits one to determine the general trends with pressure and temperature. When an overall rate expression is used to approximate real hydrocarbon oxidation kinetics experimental results, the activation energy of the overall process is found to be high—of the order of 160 kJ/mol. Thus, the exponential in the flame speed equation is sensitive to variations in the flame temperature. This sensitivity is the dominant temperature effect on flame speed. There is also, of course, an effect of temperature on the diffusivity; generally, the diffusivity is considered to vary with the temperature to the 1.75 power.

The pressure dependence of flame speed as developed from the thermal approaches was given by the expression

$S_{L} \sim {(P^{n - 2})}^{1 / 2}$ $S_{L} \sim {(P^{n - 2})}^{1 / 2}$

(4.23)

where n was the overall order of reaction. Thus, for second-order reactions the flame speed appears independent of pressure. In observing experimental measurements of flame speed as a function of pressure, one must determine whether the temperature was kept constant with inert dilution. As the pressure is increased, dissociation decreases and the temperature rises. This effect must be considered in the experiment. For hydrocarbon–air systems, however, the temperature varies little from atmospheric pressure and above owing to a minimal amount of dissociation. There is a more pronounced temperature effect at subatmospheric pressures.

To a first approximation one could perhaps assume that hydrocarbon–air reactions are second-order. Although it is impossible to develop a single overall rate expression for the complete experimental range of temperatures and pressures used by various investigators, values have been reported and hold for the limited experimental ranges of temperature and pressure from which the expression was derived. The overall reaction orders reported range from 1.5 to 2.0, and most results are around 1.75 [2,23]. Thus, it is not surprising that experimental results show a decline in flame speed with increasing pressure [2].

As briefly mentioned earlier, with the background developed in the detailed studies of hydrocarbon oxidation, it is possible to explain this pressure trend more thoroughly. Recall that the key chain branching reaction in any hydrogen-containing system is the following reaction (Chapter 3, reaction (3.21)):

$H + O_{2} \to O + OH$ $H + O_{2} \to O + OH$

(4.64)

Any process that reduces the H atom concentration and any reaction that competes with reaction (4.64) for H atoms will tend to reduce the overall oxidation rate; that is, it will inhibit combustion. As discussed in Chapter 3 (reaction (3.25)), reaction (4.65)

$H + O_{2} + M \to H O_{2} + M$ $H + O_{2} + M \to H O_{2} + M$

(4.65)

competes directly with reaction (4.64). Reaction (4.65) is third-order and therefore much more pressure-dependent than reaction (4.64). Consequently, as pressure is increased, reaction (4.65) essentially inhibits the overall reaction and reduces the flame speed. Figure 4.20 reports the results of some analytical calculations of flame speeds in which detailed kinetics were included; the results obtained are consistent with recent measurements [2]. For pressures below atmospheric, there is only a small decrease in flame speed as the pressure is increased; and at higher pressure (1–5 atm), the decline in S_L with increasing pressure becomes more pronounced. The reason for this change of behavior is twofold. Below atmospheric pressure, reaction (4.65) does not compete effectively with reaction (4.64), and any decrease owing to reaction (4.65) is compensated by a rise in temperature. Above 1 atm reaction (4.65) competes effectively with reaction (4.64); temperature variation with pressure in this range is slight, and thus a steeper decline in S_L with pressure is found. Since the kinetic and temperature trends with pressure exist for all hydrocarbons, the same pressure effect on S_L will exist for all such fuels.

Figure 4.20 Variation in laminar flame speeds with pressure for some stoichiometric fuel–air mixtures. After Westbrook and Dryer [2].

Even though S_L decreases with increasing pressure for the conditions described,

{\dot{m}}_{0}

${\dot{m}}_{0}$

increases with increasing pressure because of the effect of pressure on ρ₀. And for higher O₂ concentrations, the temperature rises substantially, about 30% for pure O₂; thus, the point where reaction (4.65) can affect the chain branching step reaction (4.64) goes to much higher pressure. Consequently, in oxygen-rich systems S_L almost always increases with pressure.

The variation of flame speed with equivalence ratio follows the variation with temperature. Since flame temperatures for hydrocarbon–air systems peak slightly on the fuel-rich side of stoichiometric (as discussed in Chapter 1), so do the flame speeds. In the case of hydrogen–air systems, the maximum S_L falls well on the fuel-rich side of stoichiometric, since excess hydrogen increases the thermal diffusivity substantially. Hydrogen gas with a maximum value of 325 cm/s has the highest flame speed in air of any other fuel.

Reported flame speed results for most fuels vary somewhat with the measurement technique used. Most results, however, are internally consistent. Plotted in Figure 4.21 are some typical flame speed results as a function of the stoichiometric mixture ratio. Detailed data, which were given in recent combustion symposia, are available in the extensive tabulations of Refs [24–26]. The flame speeds for many fuels in air have been summarized from these references and are listed in Appendix F. Since most paraffins, except methane, have approximately the same flame temperature in air, it is not surprising that their flame speeds are about the same (∼45 cm/s). Methane has a somewhat lower speed (<40 cm/s). Attempts [24] have been made to correlate flame speed with hydrocarbon fuel structure and chain length, but these correlations appear to follow the general trends of temperature. Olefins, having the same C/H ratio, have the same flame temperature (except for ethene, which is slightly higher) and have flame speeds of approximately 50 cm/s. In this context, ethene has a flame speed of approximately 75 cm/s. Owing to its high flame temperature, acetylene has a maximum flame speed of about 160 cm/s. As mentioned previously, molecular hydrogen peaks far into the fuel-rich region because of the benefit of the fuel diffusivity. Wet carbon monoxide favors the rich side because the net rate of the termination reaction H + CO + M → HCO + M is much slower than the termination step H + O₂ + M → HO₂ + M, which would prevail in the lean region.

Figure 4.21 General variation in laminar flame speeds with equivalence ratio ϕ for various fuel–air systems at P = 1 atm and T₀ = 298 K.

The variation of flame speed with oxygen concentration poses further questions about the factors that govern the flame speed. Shown in Figure 4.22 is the flame speed of a fuel in various oxygen–nitrogen mixtures relative to its value in air. Note the 10-fold increase for methane between pure oxygen and air, the 7.5-fold increase for propane, the 3.4-fold increase for hydrogen, and the 2.4-fold increase for carbon monoxide. From the effect of temperature on the overall rates and diffusivities, one would expect about a fivefold increase for all these fuels. Since the CO results contain a fixed amount of hydrogen additives [24], the fact that the important OH radical concentration does not increase as much as expected must play a role in the lower rise. Perhaps for general considerations the hydrogen values are near enough to a general estimate. Indeed, there is probably a sufficient radical pool at all oxygen concentrations. For the hydrocarbons, the radical pool concentration undoubtedly increases substantially as one goes to pure oxygen for two reasons—increased temperature and no nitrogen dilution. Thus, applying the same general rate expression for air and oxygen just does not suffice.

Figure 4.22 Relative effect of oxygen concentrations on flame speed for various fuel–air systems at P = 1 atm and T₀ = 298 K. After Zebatakis [25].

The effect of the initial temperature of a premixed fuel–air mixture on the flame propagation rate again appears to be reflected through the final flame temperature. Since the chemical energy release is always so much greater than the sensible energy of the reactants, small changes of initial temperature generally have little effect on the flame temperature. Nevertheless, the flame propagation expression contains the flame temperature in an exponential term; thus, as discussed many times previously, small changes in flame temperature can give noticeable changes in flame propagation rates. If the initial temperatures are substantially higher than normal ambient, the rate of reaction (4.65) can be reduced in the preheat zone. Since reaction (4.65) is one of recombination, its rate decreases with increasing temperature, and so the flame speed will be enhanced even further.

Perhaps the most interesting set of experiments to elucidate the dominant factors in flame propagation was performed by Clingman et al. [27]. Their results clearly show the effect of the thermal diffusivity and reaction rate terms. These investigators measured the flame propagation rate of methane in various oxygen-inert gas mixtures. The mixtures of oxygen to inert gas were 0.21/0.79 on a volumetric basis, the same as that which exists for air. The inerts chosen were nitrogen (N₂), helium (He), and argon (Ar). The results of these experiments are shown in Figure 4.23.

Figure 4.23 Methane laminar flame velocities in various inert gas–oxygen mixtures. After Clingman et al. [27].

The trends of the results in Figure 4.23 can be readily explained. Argon and nitrogen have thermal diffusivities that are approximately equal. However, Ar is a monatomic gas whose specific heat is lower than that of N₂. Since the heat release in all systems is the same, the final (or flame) temperature will be higher in the Ar mixture than in the N₂ mixture. Thus, S_L will be higher for Ar than for N₂. Argon and helium are both monatomic, so their final temperatures are equal. However, the thermal diffusivity of He is much greater than that of Ar. Helium has a higher thermal conductivity and a much lower density than argon. Consequently, S_L for He is much greater than that for Ar.

The effect of chemical additives on the flame speed has also been explored extensively. Leason [28] reported the effects on flame velocity of small concentrations of additive (<3%) and other fuels. He studied the propane–air flame. Among the compounds considered were acetone, acetaldehyde, benzaldehyde, diethyl ether, benzene, and carbon disulfide. In addition, many others were chosen from those classes of compounds that were shown to be oxidation intermediates in low-temperature studies; these compounds were expected to decrease the induction period and thus increase the flame velocity. Despite differences in apparent oxidation properties, all the compounds studied changed the flame velocity in exactly the same way that dilution with excess fuel would on the basis of oxygen requirement. These results support the contention that the laminar flame speed is controlled by the high-temperature reaction region. The high temperatures generate more than ample radicals via chain branching, so it is unlikely that any additive could contribute any reaction rate accelerating feature.

There is, of course, a chemical effect in carbon monoxide flames. This point was mentioned in the discussion of carbon monoxide explosion limits. Studies have shown that CO flame velocities increase appreciably when small amounts of hydrogen, hydrogen-containing fuels, or water are added. For 45% CO in air, the flame velocity passes through a maximum after approximately 5% by volume of water has been added. At this point, the flame velocity is 2.1 times the value with 0.7% H₂O added. After the 5% maximum is attained, a dilution effect begins to cause a decrease in flame speed. The effect and the maximum arise because a sufficient steady-state concentration of OH radicals must be established for the most effective explosive condition.

Although it may be expected that the common antiknock compounds would decrease the flame speed, no effects of antiknocks have been found in constant pressure combustion. The effect of the inhibition of the preignition reaction on flame speed is of negligible consequence. There is no universal agreement on the mechanism of antiknocks, but it has been suggested that they serve to decrease the radical concentrations by absorption on particle surfaces (see Chapter 2). The reduction of the radical concentration in the preignition reactions or near the flammability limits can severely affect the ability to initiate combustion. In these cases the radical concentrations are such that the chain branching factor is close to the critical value for explosion. Any reduction could prevent the explosive condition from being reached. Around the stoichiometric mixture ratio, the radical concentrations are normally so great that it is difficult to add any small amounts of additives that would capture enough radicals to alter the reaction rate and the flame speed.

Certain halogen compounds, such as the Freons, are known to alter the flammability limits of hydrocarbon–air mixtures. The accepted mechanism is that the halogen atoms trap hydrogen radicals necessary for the chain branching step. Near the flammability limits, conditions exist in which the radical concentrations are such that the chain branching factor α is just above α_crit. Any reduction in radicals and the chain branching effects these radicals engender could eliminate the explosive (fast reaction rate and larger energy release rate) regime. However, small amounts of halogen compounds do not seem to affect the flame speed in a large region around the stoichiometric mixture ratio. The reason is, again, that in this region the temperatures are so high and radicals so abundant that elimination of some radicals does not affect the reaction rate.

It has been found that some of the larger halons (the generic name for the halogenated compounds sold under commercial names such as Freon) are effective flame suppressants. Also, some investigators have found that inert powders are effective in firefighting. Fundamental experiments to evaluate the effectiveness of the halons and powders have been performed with various types of apparatus that measure the laminar flame speed. Results have indicated that the halons and the powders reduce flame speeds even around the stoichiometric air–fuel ratio. The investigators performing these experiments have argued that those agents are effective because they reduce the radical concentrations. However, this explanation could be questioned. The quantities of these added agents are great enough that they could absorb sufficient amounts of heat to reduce the temperature and hence the flame speed. Both halons and powders have large total heat capacities.

..................Content has been hidden....................

You can't read the all page of ebook, please click here login for view all page.

Table of Contents for 4.3. Laminar Flame Speed

Create new playlist

Sign In

Sign Up

4.3. Laminar Flame Speed

4.3.1. Theory of Mallard and Le Chatelier

4.3.2. Theory of Zeldovich, Frank–Kamenetskii, and Semenov

4.3.3. Comprehensive Theory and Laminar Flame Structure Analysis

4.3.4. Laminar Flame and Energy Equation

4.3.5. Flame Speed Measurements

4.3.5.1. Burner method

4.3.5.2. Cylindrical tube method

4.3.5.3. Soap bubble method

4.3.5.4. Closed spherical bomb method

4.3.5.5. Flat flame burner method

4.3.6. Experimental Results—Physical and Chemical Effects

Table of Contents for
4.3. Laminar Flame Speed