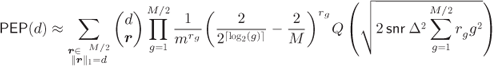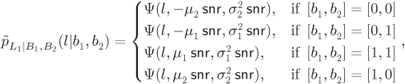6.4 Performance Evaluation of BICM via Gaussian Approximations
Two major handicaps of the numerical integration we discussed at the end of Section 6.3.1 were removed in Sections 6.3.2 and 6.3.3. However, the problem of a direct connection between the PEP and the parameters of the constellation and/or labeling still remains. In order to solve this problem, in this section we use the simplified Gaussian forms for the PDF we derived in Section 5.5.
6.4.1 PEP Calculation using Gaussian Approximations
For ![]() PAM and
PAM and ![]() PSK constellations labeled by the BRGC, we showed in Section 5.5 that we may use Gaussian functions to approximate the PDF of the L-values conditioned on the transmitted symbols. More specifically, for a given transmitted symbol
PSK constellations labeled by the BRGC, we showed in Section 5.5 that we may use Gaussian functions to approximate the PDF of the L-values conditioned on the transmitted symbols. More specifically, for a given transmitted symbol ![]() , we have
, we have
where ![]() ,
, ![]() and
and ![]() depend on the transmitted symbol
depend on the transmitted symbol ![]() , bit position
, bit position ![]() , constellation
, constellation ![]() , labeling
, labeling ![]() , and adopted approximation model (consistent model (CoM) or zero-crossing model (ZcM)). The mean values and variances
, and adopted approximation model (consistent model (CoM) or zero-crossing model (ZcM)). The mean values and variances ![]() and
and ![]() in (6.368) are given in Tables 5.1 and 5.2 for
in (6.368) are given in Tables 5.1 and 5.2 for ![]() PAM and
PAM and ![]() PSK, respectively.
PSK, respectively.
The PDF of the L-values conditioned on the transmitted bit ![]() can then be obtained via marginalization, i.e.,
can then be obtained via marginalization, i.e.,
where (6.370) follows from (6.368) and (2.77). In (6.370) we use a factor ![]() to take into account that the same PDF approximation will be obtained in each of
to take into account that the same PDF approximation will be obtained in each of ![]() “groups” of symbols in the constellation labeled by the BRGC for a given
“groups” of symbols in the constellation labeled by the BRGC for a given ![]() (see more details in Section 5.5.4).
(see more details in Section 5.5.4).
By inspecting Tables 5.1–5.2, it is possible to see that for a given ![]() , the possible values of
, the possible values of ![]() and
and ![]() obtained for
obtained for ![]() include those obtained for
include those obtained for ![]() , which in turn include those obtained for
, which in turn include those obtained for ![]() , and so on. In otherwords, the set of mean and variances obtained for
, and so on. In otherwords, the set of mean and variances obtained for ![]() covers the mean and variances for
covers the mean and variances for ![]() . Thus, for simplicity, and assuming there are at most
. Thus, for simplicity, and assuming there are at most ![]() different Gaussian PDFs, we define
different Gaussian PDFs, we define ![]() and
and ![]() as the mean and variance of the
as the mean and variance of the ![]() th Gaussian PDF. Furthermore, we assume
th Gaussian PDF. Furthermore, we assume ![]() , and
, and ![]() .14 We can then express the PDFs (6.370) as the following Gaussian mixture
.14 We can then express the PDFs (6.370) as the following Gaussian mixture
where the proportion of ![]() th Gaussian PDFs in the mixture, denoted by
th Gaussian PDFs in the mixture, denoted by ![]() , can be interpreted as the probability that the L-value
, can be interpreted as the probability that the L-value ![]() is distributed according to the
is distributed according to the ![]() th Gaussian PDF.
th Gaussian PDF.
We can gather the weighting factors ![]() in a matrix
in a matrix
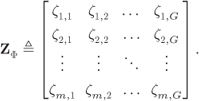
The parameters of the ![]() th Gaussian PDF uniquely depend on the ED between the symbol
th Gaussian PDF uniquely depend on the ED between the symbol ![]() and the closest symbol in
and the closest symbol in ![]() , and therefore, the elements of
, and therefore, the elements of ![]() may be seen as a generalization of the EDS
may be seen as a generalization of the EDS ![]() defined in Section 2.5.1. We will thus refer to
defined in Section 2.5.1. We will thus refer to ![]() as a (normalized) constellation bit-wise Euclidean distance spectrum (CBEDS).
as a (normalized) constellation bit-wise Euclidean distance spectrum (CBEDS).

Figure 6.21 8PAM constellation labeled by the BRGC. The EDs that are relevant from the point of view of obtaining the CBEDS  are shown for the subconstellation
are shown for the subconstellation  for (a)
for (a)  , (b)
, (b)  , and (c)
, and (c) 
Under the quasirandom interleaving assumption, the PDF ![]() in (6.227) can be expressed using (6.371) as
in (6.227) can be expressed using (6.371) as
where
has a meaning of the probability that an L-value passed to the decoder is distributed according to the ![]() th Gaussian PDF. Later in this section we compute
th Gaussian PDF. Later in this section we compute ![]() for
for ![]() PAM and
PAM and ![]() PSK constellations.
PSK constellations.
With a closed-form approximation for the PDF of ![]() in (6.377), we are ready to compute the PDF of
in (6.377), we are ready to compute the PDF of ![]() in (6.283). This is done as follows:
in (6.283). This is done as follows:
where (6.381) follows from reorganizing the terms in (6.380), and where ![]() in
in ![]() denotes the number of L-values distributed according to the
denotes the number of L-values distributed according to the ![]() th Gaussian PDF.
th Gaussian PDF.
Using (6.381) in (6.282) we find

The PEP approximation in (6.383) is in closed-form; however, for large values of ![]() and/or
and/or ![]() , the enumeration of all the terms in (6.383) becomes tedious. This can be simplified by taking only the Q-function with the smallest argument, which is an approximation that will be tight for
, the enumeration of all the terms in (6.383) becomes tedious. This can be simplified by taking only the Q-function with the smallest argument, which is an approximation that will be tight for ![]() . This dominant Q-function is obtained for
. This dominant Q-function is obtained for ![]() , i.e., when all the
, i.e., when all the ![]() L-values are distributed according to the Gaussian PDF with the smallest mean value (
L-values are distributed according to the Gaussian PDF with the smallest mean value (![]() ). The PEP in (6.383) is then approximated as
). The PEP in (6.383) is then approximated as
Finally, from (6.225) we obtain a closed-form approximation for the BEP in BICM
where ![]() can be evaluated using either (6.383) or (6.384). To evaluate (6.385), we need the IDS of the binary encoder, the weighting coefficients
can be evaluated using either (6.383) or (6.384). To evaluate (6.385), we need the IDS of the binary encoder, the weighting coefficients ![]() and the parameters of the Gaussian approximations
and the parameters of the Gaussian approximations ![]() and
and ![]() . In the following, we particularize the results in this section to
. In the following, we particularize the results in this section to ![]() PAM and
PAM and ![]() PSK constellations.
PSK constellations.
6.4.2 MPAM Constellations
For ![]() PAM labeled by the BRGC, we have
PAM labeled by the BRGC, we have ![]() and by generalizing Example 6.33, we obtain
and by generalizing Example 6.33, we obtain
for ![]() . The mean values and variances are obtained from Table 5.1 as
. The mean values and variances are obtained from Table 5.1 as
and ![]() in (6.378) is
in (6.378) is
where ![]() .
.
Using (6.391) we express (6.383) as
for CoM and
for ZcM.
The simplified PEP approximation in (6.384) (the same result is obtained by applying CoM and ZcM) for ![]() PAM is then given by
PAM is then given by
where we used (2.47). We can thus conclude that an increase on the size of the constellation ![]() reduces the multiplicative factor before the Q-function. More importantly, an increase of
reduces the multiplicative factor before the Q-function. More importantly, an increase of ![]() by one is equivalent to decreasing the SNR by
by one is equivalent to decreasing the SNR by ![]() . This SNR shift will dominate the behavior of the BEP at high SNR.
. This SNR shift will dominate the behavior of the BEP at high SNR.
The following example show the approximations for particular values of ![]() .
.
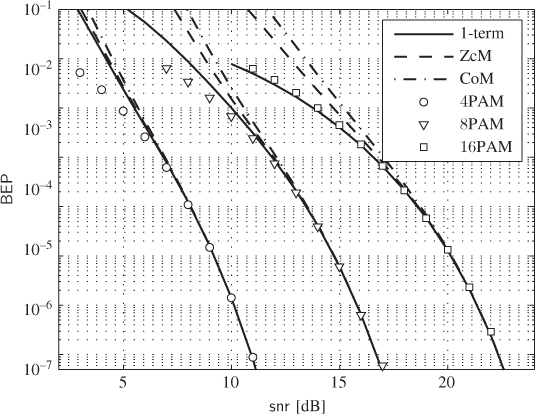
Figure 6.22 BEP approximations (lines) and simulations (markers) for a CENC with 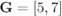 over the AWGN channel: 4PAM (circles), 8PAM (triangles) and 16PAM (squares). The dashed and dashed-dotted lines are the approximations obtained using (6.392) and (6.393) and the “1-term” approximation is obtained using the single-term expressions for the PEP shown in (6.399)–(6.401)
over the AWGN channel: 4PAM (circles), 8PAM (triangles) and 16PAM (squares). The dashed and dashed-dotted lines are the approximations obtained using (6.392) and (6.393) and the “1-term” approximation is obtained using the single-term expressions for the PEP shown in (6.399)–(6.401)
6.4.3 MPSK Constellations
In the case of ![]() PSK, we know that
PSK, we know that ![]() and from Table 5.2 we read
and from Table 5.2 we read
and knowing that the PDF of ![]() is the same as the PDF of
is the same as the PDF of ![]() (see also Example 5.7), we have
(see also Example 5.7), we have
and
for ![]() .
.
In analogy to (6.391) we can find ![]() as
as
where ![]() .
.
The results above show that in the case of ![]() PSK constellations, the L-values can again be approximated as a Gaussian mixture, where the parameters of the Gaussian PDFs as well as the weights are known in closed form. Using these closed-form expressions, it is possible to repeat the analysis we presented before, which we do not include here as it is mostly a repetition of the developments for
PSK constellations, the L-values can again be approximated as a Gaussian mixture, where the parameters of the Gaussian PDFs as well as the weights are known in closed form. Using these closed-form expressions, it is possible to repeat the analysis we presented before, which we do not include here as it is mostly a repetition of the developments for ![]() PAM in Section 6.4.2.
PAM in Section 6.4.2.
6.4.4 Case Study: BEP for Constellation Rearrangement
We consider here transmission with the so-called constellation rearrangement (CoRe), which is used in hybrid automatic repeat request (HARQ). When errors are detected in the received codeword, the same codeword is retransmitted, but the binary labeling of the constellation is changed. The constellation is therefore “rearranged”, hence the name CoRe. In what follows we briefly outline the principles of CoRe in the case of 4PAM; this is equivalent to using 16QAM labeled by the BRGC.
We will use the Gaussian model of the L-values we showed in Example 5.19. More specifically, we reorganize the term from (5.197) and (5.198) and explicitly condition on the bits ![]() and
and ![]() :
:
Using (6.409) and (6.410), we make two key observations:
- The L-value
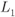 has a “high-protection” distribution
has a “high-protection” distribution  if
if 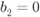 and a “low-protection” distribution
and a “low-protection” distribution 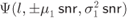 if
if 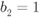 .
. - The L-value
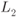 has always a low-protection distribution, irrespective of the value of the transmitted bits.
has always a low-protection distribution, irrespective of the value of the transmitted bits.
CoRe can be then seen as a process that equalizes the “protection” experienced by the bits passing through the different bit positions in different transmissions. This is possible because in each transmission the same bits ![]() and
and ![]() are transmitted. More specifically, CoRe is based on two operations: negation of the bit at position
are transmitted. More specifically, CoRe is based on two operations: negation of the bit at position ![]() (i.e., negation of the second row of the matrix
(i.e., negation of the second row of the matrix ![]() ) and swapping the position of the labels of
) and swapping the position of the labels of ![]() and
and ![]() (i.e., swapping the first and second row of
(i.e., swapping the first and second row of ![]() ).
).
The negation operation is connected with the first observation we made above: as depending on the value of ![]() the L-value
the L-value ![]() changes its distribution, using
changes its distribution, using ![]() in the first transmission and
in the first transmission and ![]() in the next one, we can guarantee that “high” protection is offered to the bit
in the next one, we can guarantee that “high” protection is offered to the bit ![]() in one out of the two transmissions.
in one out of the two transmissions.
The swapping responds to the second observation we made above, and is meant to transmit the bits ![]() at position
at position ![]() so that
so that ![]() can take advantage of the “high” protection offered in that bit position.
can take advantage of the “high” protection offered in that bit position.
At the receiver, the L-values for different transmissions are calculated, negated and/or swapped (if necessary), and then added to form aggregated CoRe L-values ![]() .15 These L-values are then passed to the decoder. After
.15 These L-values are then passed to the decoder. After ![]() transmissions, we obtain the following distributions for
transmissions, we obtain the following distributions for ![]()

and for ![]()
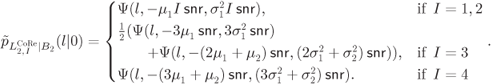
The PDF of the L-values passed to the decoder is then given by
where
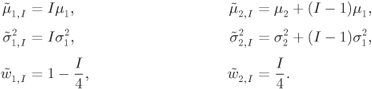
Since the PDF in (6.414) is again a Gaussian mixture, an approximation similar to the one in (6.398) may be used
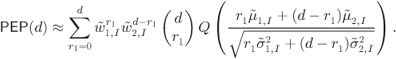
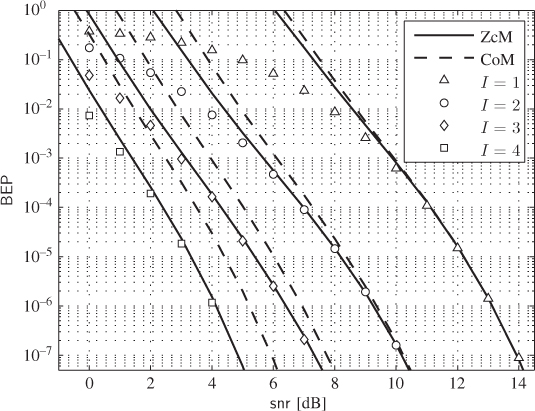
Figure 6.23 BEP approximations using the ZcM (solid lines) and the CoM (dashed lines) for a CENC with 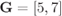 over an AWGN channel with CoRe and
over an AWGN channel with CoRe and 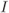 retransmissions. The simulation results are shown with markers:
retransmissions. The simulation results are shown with markers: 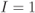 (triangles),
(triangles), 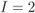 (circles),
(circles),  (diamonds), and
(diamonds), and 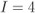 (squares)
(squares)
In Fig. 6.23 the results obtained via numerical simulations are contrasted against the approximations of the PEP in (6.392) and (6.393). Unlike in Fig. 6.22, the differences between ZcM and CoM are now very clear. The ZcM provides a tight approximation on the coded BEP, especially when the number of transmissions increases. In particular, for ![]() ,
, ![]() and
and ![]() have the same PDF and
have the same PDF and ![]() and
and ![]() have to be used in the model. Thus, HARQ accentuates the importance of the adequate modeling of the “high-protection” effect. Note that without HARQ and CoRe, the effect of “high-protection” is less pronounced and can be even neglected, e.g., using the one-term “low-protection” approximation (6.399). In the presence of CoRe we cannot do this because for
have to be used in the model. Thus, HARQ accentuates the importance of the adequate modeling of the “high-protection” effect. Note that without HARQ and CoRe, the effect of “high-protection” is less pronounced and can be even neglected, e.g., using the one-term “low-protection” approximation (6.399). In the presence of CoRe we cannot do this because for ![]() we have
we have ![]() , i.e., the “low-protection” is entirely removed.
, i.e., the “low-protection” is entirely removed.
6.5 Bibliographical Notes
Performance evaluation in uncoded transmission has been the focus of research for many decades. The initial approximations of the SEP [1] were later replaced by calculations for regularly spaced constellations ![]() QAM and/or
QAM and/or ![]() PSK [2 3]. In this chapter we showed expression for
PSK [2 3]. In this chapter we showed expression for ![]() . The calculation of the BEP for 3D constellations was considered in [4].
. The calculation of the BEP for 3D constellations was considered in [4].
The BEP for uncoded transmission in (6.28) has been studied in detail in [5 6], where the asymptotic optimality of the BRGC for regular constellations is proved. Significant efforts have been made to evaluate the BEP in fading channels, i.e., to average the expressions for the AWGN channel over the fading distribution. This was considered, e.g., in [7–10]. Some of the formulas we presented in this chapter were shown, for integer ![]() in [11, eq. (6)], for half-integer
in [11, eq. (6)], for half-integer ![]() in [12, eq. (15)], and for arbitrary
in [12, eq. (15)], and for arbitrary ![]() (using hypergeometric functions) in [13]. The literature is abundant in this area, so it is in fact quite difficult to recognize all the contributions. For a hopefully more complete list, we refer the reader to [14].
(using hypergeometric functions) in [13]. The literature is abundant in this area, so it is in fact quite difficult to recognize all the contributions. For a hopefully more complete list, we refer the reader to [14].
An alternative representation of the bivariate Q-function (6.99) was shown in [15] and the identity (6.102), simplified with respect to [16, eq. (11)], via the use of Q-functions. The form (6.99) is called Craig's form after the author of [17], who derived first a simple alternative form of Q-function we showed in (6.108).
The error event appearing in (6.173) is sometimes called “first-error event” [18, Section 6.2], [19, Section I], [20, Section 12.2] or error probability per node [21, Section 4.3]. The upper bound on the WEP in the case of the TCM transmissions can be found in [18, eq. ((6.6))], [20, eq. (12.20)], [22, eq. ((4.1))]. The expressions for the WEP in (6.178) and (6.241) are straightforward generalizations of the bound presented in [23] for CCs. TCM encoders with optimal distance spectrum (similar to the ones we used in Example 6.16) were presented in [24].
The expression in (6.243) is the most common expression for the upper bound for BICM, cf. [25, eq. (26)], [26, eq. (4.12)]. The upper bound in (6.243) can be found in almost any existing book on digital communications or coding (see, e.g., [20, eq. (12.28)], [27, eq. (7.9)], [28, eq. ((8.2)–19)], and it was originally defined for channels in which the metrics for the code bits passed to the decoder are i.i.d., e.g., 2PAM over the AWGN channel, in which the conditional L-values follow a Gaussian distribution as shown in(3.63).
The performance analysis of BICM transmission under random infinite-length interleaving proposed in [25] has been widely adopted in the literature. As we have seen, this analysis can be used in the case of a fixed interleaver if the assumptions of quasirandomness are fulfilled. On the other hand, finite-length interleaving has received much less attention. PEP calculations for infinite-length (but random) interleaving have been presented in [26, Chapter 4.3].
A formal analysis of the relationship between the spectrum of the code, the finite-length interleaving, and the performance in terms of WEP/BEP still seems to be missing in the literature. However, while this issue may be interesting from a theoretical point of view, its practical importance is often negligible as we argued in Section 6.2.5. This is particularly true for capacity-approaching codes such as TCs, for which we can eliminate the finite-length related terms from the WEP expression in (6.214) (see Lemma 6.19). This follows from the fact that the spectrum ![]() of such codes decreases with
of such codes decreases with ![]() , which has been shown, e.g., in [29, Fig. 10].
, which has been shown, e.g., in [29, Fig. 10].
Insights into the gains of BICM over TCM were first shown in [30] via bounding techniques. In [31] the PEP was evaluated via direct/inverse Laplace transforms. This idea was refined in [32 33]. The formal derivation of the SPA we presented in Section 6.3.2 may be found in [34, Chapter 2], and the intuitive approach we showed was presented in [33, Appendix I]. The SPA was used for PEP evaluation in [33], where Monte Carlo integration was suggested to calculate the MGF and its derivatives. The SPA was then used in [35] for 2PAM and fading channels and later reused in [36 37], where closed-form formulas were obtained thanks to the analytical description of the PDFs of the L-values. The use of (zero-crossing or consistent) Gaussian approximations to simplify the integration was made popular in [38]. The zero-crossing approximation is due to [39], where it was first applied to analyze uncoded HARQ transmission based on the CoRe.
The CBEDS we used in this chapter was first introduced in [40 41] where all the binary labelings for 8PSK having a different CBEDS were classified. The same concept was also presented in [42, Chapter 4]. The CBEDS in fact corresponds to a generalization of the ED spectrum of [43] in the sense that it considers the bit positions separately.
Mapping diversity has been studied, e.g., in [44–47]. CoRe was recommended by the third-generation partnership project (3GPP) working group because of its simplicity [48] and is only slightly suboptimal when compared to metrics calculation based on the outcomes of all transmissions (as required in other mapping diversity schemes). Moredetails about CoRe may be found in [49]. Various mapping diversity schemes are analyzed from an information-theoretic point of view in [50].
The WD and the IWD we used for CENCs in Example 6.22 can be extended to turbo encoders (TENCs) using the concept of uniform and random interleaver introduced in [51 52]. For the numerical results in this chapter, we used a breadth-first search algorithm [53]. Alternatively, a transfer function approach could be used, which works well for small values of memories ![]() . For large values of
. For large values of ![]() the Bayesian evolutionary analysis by sampling trees (BEAST) algorithm recently introduced in [54] (see also [55]) is more appropriate.
the Bayesian evolutionary analysis by sampling trees (BEAST) algorithm recently introduced in [54] (see also [55]) is more appropriate.
References
- [1] Foschini, G. J., Gitlin, R. D., and Weinstein, S. B. (1974) Optimization of two-dimensional signal constellations in the presence of Gaussian noise. IEEE Trans. Commun., 22 (1), 28–38.
- [2] Lassing, J., Ström, E. G., Agrell, E., and Ottosson, T. (2003) Computation of the exact bit error rate of coherent M-ary PSK with Gray code bit mapping. IEEE Trans. Commun., 51 (11), 1758–1760.
- [3] Lassing, J. (2005) On the labeling of signal constellations. PhD dissertation, Chalmers University of Technology, Göteborg, Sweden.
- [4] Khabbazian, M., Hossain, M. J., Alouini, M. S., and Bhargava, V. K. (2009) Exact method for the error probability calculation of three-dimensional signal constellations. IEEE Trans. Commun., 57 (4), 922–925.
- [5] Agrell, E., Lassing, J., Ström, E. G., and Ottosson, T. (2004) On the optimality of the binary reflected Gray code. IEEE Trans. Inf. Theory, 50 (12), 3170–3182.
- [6] Agrell, E., Lassing, J., Ström, E. G., and Ottosson, T. (2007) Gray coding for multilevel constellations in Gaussian noise. IEEE Trans. Inf. Theory, 53 (1), 224–235.
- [7] Simon, M. and Alouini, M. S. (1998) A simple single integral representation of the bivariate Rayleigh distribution. IEEE Commun. Lett., 2 (5), 128–130.
- [8] Alouini, M. S. and Goldsmith, A. J. (1999) A unified approach for calculating error rates of linearly modulated signals over generalized fading channels. IEEE Trans. Commun., 47 (9), 1324–1334.
- [9] Dong, X., Beaulieu, N. C., and Wittke, P. H. (1999) Error probabilities of two-dimensional
 -ary signalling in fading. IEEE Trans. Commun., 47 (3), 352–355.
-ary signalling in fading. IEEE Trans. Commun., 47 (3), 352–355. - [10] Annamalai, A., Tellambura, C., and Bhargava, V. K. (2005) A general method for calculating error probabilities over fading channels. IEEE Trans. Commun., 53 (5), 841–852.
- [11] Annamalai, A. and Tellambura, C. (2001) Error rates for Nakagami-
 fading multichannel reception of binary and
fading multichannel reception of binary and  -ary signals. IEEE Trans. Commun., 49 (1), 58–68.
-ary signals. IEEE Trans. Commun., 49 (1), 58–68. - [12] Xu, H., Benjillali, M., and Szczecinski, L. (2008) Closed-form expression for the bit error rate in rectangular QAM with arbitrary constellation mapping in transmissions over Nakagami-
 fading channel. Wiley J. Wireless Commun. Mob. Comput., 8 (1), 93–99.
fading channel. Wiley J. Wireless Commun. Mob. Comput., 8 (1), 93–99. - [13] Shin, H. and Lee, J. H. (2004) On the error probability of binary and M-ary signals in Nakagami-m fading channels. IEEE Trans. Commun., 52 (4), 536–539.
- [14] Simon, M. K. and Alouini, M.-S. (2000) Digital Communications Over Fading Channels: A Unified Approach to Performance Analysis, 1st edn, John Wiley & Sons, Inc., New York.
- [15] Simon, M. K. (2002) A simpler form of the Craig representation for the two-dimensional joint Gaussian Q-function. IEEE Commun. Lett., 6 (2), 49–51.
- [16] Zhong, L., Alajaji, F., and Takahara, G. (2005) Error analysis for nonuniform signaling over Rayleigh fading channels. IEEE Trans. Commun., 53 (1), 39–43.
- [17] Craig, J. W. (1991) A new, simple and exact result for calculating the probability of error for two-dimensional signal constellations. Military Communications Conference (MILCOM), November 1991, McLean, VA.
- [18] Schlegel, C. B. and Perez, L. C. (2004) Trellis and Turbo Coding, 1st edn, John Wiley & Sons.
- [19] Rouanne, M. and Costello, D. J. Jr. (1989) An algorithm for computing the distance spectrum of trellis codes. IEEE J. Sel. Areas Commun., 7 (6), 929–940.
- [20] Lin, S. and Costello, D. J. Jr. (2004) Error Control Coding, 2nd edn, Prentice Hall, Englewood Cliffs, NJ.
- [21] Viterbi, A. J. and Omura, J. K. (1979) Principles of Digital Communications and Coding, McGraw-Hill.
- [22] Benedetto, S. and Biglieri, E. (1999) Principles of Digital Transmission with Wireless Applications, Kluwer Academic.
- [23] Caire, G. and Viterbo, E. (1998) Upper bound on the frame error probability of terminated trellis codes. IEEE Commun. Lett., 2 (1), 2–4.
- [24] Alvarado, A., Graell i Amat, A., Brännström, F., and Agrell, E. (2013) On optimal TCM encoders. IEEE Trans. Commun., 61 (6), 2178–2189.
- [25] Caire, G., Taricco, G., and Biglieri, E. (1998) Bit-interleaved coded modulation. IEEE Trans. Inf. Theory, 44 (3), 927–946.
- [26] Guillén i Fàbregas, A., Martinez, A., and Caire, G. (2008) Bit-interleaved coded modulation. Found. Trends Commun. Inf. Theory, 5 (1–2), 1–153.
- [27] Burr, A. (2001) Modulation and Coding for Wireless Communications, Prentice Hall.
- [28] Proakis, J. G. and Salehi, M. (2008) Digital Communications, 5th edn, McGraw-Hill.
- [29] Perez, L. C., Seghers, J., and Costello, D. J. Jr. (1996) A distance spectrum interpretation of turbo codes. IEEE Trans. Inf. Theory, 42 (16), 1698–1709.
- [30] Zehavi, E. (1992) 8-PSK trellis codes for a Rayleigh channel. IEEE Trans. Commun., 40 (3), 873–884.
- [31] Biglieri, E., Caire, G., Taricco, G., and Ventura-Traveset, J. (1996) Simple method for evaluating error probabilities. Electron. Lett., 32 (2), 191–192.
- [32] Biglieri, E., Caire, G., Taricco, G., and Ventura-Traveset, J. (1998) Computing error probabilities over fading channels: A unified approach. Eur. Trans. Telecommun., 9 (1), 15–25.
- [33] Martinez, A., Guillén i Fàbregas, A., and Caire, G. (2006) Error probability analysis of bit-interleaved coded modulation. IEEE Trans. Inf. Theory, 52 (1), 262–271.
- [34] Butler, R. W. (2007) Saddlepoint Approximation with Applications, Cambridge University Press.
- [35] Martinez, A., Guillén i Fàbregas, A., and Caire, G. (2007) A closed-form approximation for the error probability of BPSK fading channels. IEEE Trans. Wireless Commun., 6 (6), 2051–2054.
- [36] Szczecinski, L., Alvarado, A., and Feick, R. (2008) Closed-form approximation of coded BER in QAM-based BICM faded transmission. IEEE Sarnoff Symposium, April 2008, Princeton, NJ.
- [37] Kenarsari-Anhari, A. and Lampe, L. (2010) An analytical approach for performance evaluation of BICM over Nakagami-
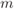 fading channels. IEEE Trans. Commun., 58 (4), 1090–1101.
fading channels. IEEE Trans. Commun., 58 (4), 1090–1101. - [38] Alvarado, A., Szczecinski, L., Feick, R., and Ahumada, L. (2009) Distribution of L-values in Gray-mapped
 -QAM: closed-form approximations and applications. IEEE Trans. Commun., 57 (7), 2071–2079.
-QAM: closed-form approximations and applications. IEEE Trans. Commun., 57 (7), 2071–2079. - [39] Benjillali, M., Szczecinski, L., Aissa, S., and Gonzalez, C. (2008) Evaluation of bit error rate for packet combining with constellation rearrangement. Wiley J. Wireless Commun. Mob. Comput., 8, 831–844.
- [40] Brännström, F. (2004) Convergence analysis and design of multiple concatenated codes. PhD dissertation, Chalmers University of Technology, Göteborg, Sweden.
- [41] Brännström, F. and Rasmussen, L. K. (2009) Classification of unique mappings for 8PSK based on bit-wise distance spectra. IEEE Trans. Inf. Theory, 55 (3), 1131–1145.
- [42] Schreckenbach, F. (2007) Iterative decoding of bit-interleaved coded modulation. PhD dissertation, Technische Universität München, Munich, Germany.
- [43] Schreckenbach, F., Görtz, N., Hagenauer, J., and Bauch, G. (2003) Optimized symbol mappings for bit-interleaved coded modulation with iterative decoding. IEEE Global Telecommunications Conference (GLOBECOM), December 2003, San Francisco, CA.
- [44] Metzner, J. (1977) Improved sequential signaling and decision techniques for nonbinary block codes. IEEE Trans. Commun., 25 (5), 561–563.
- [45] Benelli, G. (1992) A new method for integration of modulation and channel coding in an ARQ protocol. IEEE Trans. Commun., 40 (10), 1594–1606.
- [46] Szczecinski, L. and Bacic, M. (2005) Constellations design for multiple transmissions: Maximizing the minimum squared Euclidean distance. IEEE Wireless Communications and Networking Conference (WCNC), March 2005, New Orleans, LA.
- [47] Samra, H., Ding, Z., and Hahn, P. M. (2005) Symbol mapping diversity design for multiple packet transmissions. IEEE Trans. Commun., 53, 810–817.
- [48] Panasonic (2001) Enhaced HARQ method with signal constellation rearrangement. Technical Report, 3GPP TSG RAN WG1.
- [49] Wengerter, C., von Elbwart, A., Seidel, E., Velev, G., and Schmitt, M. (2002) Advanced hybrid ARQ technique employing a signal constellation rearrangement. IEEE Vehicular Technology Conference (VTC-Fall), September 2002, Vancouver, BC, Canada.
- [50] Szczecinski, L., Diop, F.-K., and Benjillali, M. (2008) On the performance of BICM with mapping diversity in hybrid ARQ. Wiley J. Wireless Commun. Mob. Comput., 8 (7), 963–972.
- [51] Benedetto, S. and Montorsi, G. (1995) Average performance of parallel concatenated block codes. Electron. Lett., 31 (3), 156–158.
- [52] Benedetto, S. and Montorsi, G. (1996) Unveiling turbo codes: Some results on parallel concatenated coding schemes. IEEE Trans. Inf. Theory, 42 (2), 409–428.
- [53] Belzile, J. and Haccoun, D. (1993) Bidirectional breadth-first algorithms for the decoding of convolutional codes. IEEE Trans. Commun., 41 (2), 370–380.
- [54] Bocharova, I. E., Handlery, M., Johannesson, R., and Kudryashov, B. D. (2004) A BEAST for prowling in trees. IEEE Trans. Inf. Theory, 50 (6), 1295–1302.
- [55] Hug, F. (2012) Codes on graphs and more. PhD dissertation, Lund University, Lund, Sweden.