2.6 Codes and Encoding
Throughout this book, we consider a rate ![]() binary encoder (see Fig. 2.18), where the information bits
binary encoder (see Fig. 2.18), where the information bits ![]() are mapped onto
are mapped onto ![]() sequences of code bits
sequences of code bits ![]() ,
, ![]() , where
, where

Figure 2.18 The encoder ENC in Fig. 2.7 has rate  and
and  different “classes” of bits
different “classes” of bits
Here, the index ![]() in the sequences
in the sequences ![]() represents a “class” of code bits sharing certain properties.5 While this description is not entirely general,6 it will allow us to highlight the encoder's properties and explain how these should be exploited during the design of BICM transceivers.
represents a “class” of code bits sharing certain properties.5 While this description is not entirely general,6 it will allow us to highlight the encoder's properties and explain how these should be exploited during the design of BICM transceivers.
The encoder is a mapper between the information sequences ![]() and the sequences
and the sequences ![]() , where
, where ![]() . The ensemble of all codewords
. The ensemble of all codewords ![]() is called a code, which we denote by
is called a code, which we denote by ![]() . In this book, we will consider linear binary codes where the relationship between the input and output bits can be defined via the generator matrix
. In this book, we will consider linear binary codes where the relationship between the input and output bits can be defined via the generator matrix ![]()
where
gathers all the code bits, and all operations are in ![]() .
.
In order to analyze the performance of a receiver which takes coding into account, we need to analyze the decoding process. The latter depends, of course, on the structure of the code, and all the other elements in the BICM system. Nevertheless, we may start with the following simplified assertion: the probability of decoding a codeword ![]() that is different from the transmitted one
that is different from the transmitted one ![]() depends on the HD
depends on the HD ![]() . This motivates the following definition of the distance spectrum (DS) of a code.
. This motivates the following definition of the distance spectrum (DS) of a code.
The next lemma particularizes Definition 2.21 to the case of linear codes.
As the HD provides an idea about how well the codewords are “protected” against decoding errors, we may also be interested in analyzing this protection for each class of code bits. This motivates the following definition of the generalized distance spectrum (GDS).
In this book, we consider two types of linear binary codes: CCs and TCs, where the codewords are obtained using a CENC and a turbo encoder (TENC), respectively.7 CCs are an example of codes which can be decoded optimally with low decoding complexity and for which we can find the DS using well-known analytical approaches. TCs, on the other hand, are an example of capacity-approaching codes, where the corresponding analytical tools coincide in part with those used for the analysis of CCs.
The encoder calculates the codewords in a deterministic manner via (2.79). However, as the input bit sequence ![]() is modeled as a sequence of i.u.d. binary random variables, the code bits
is modeled as a sequence of i.u.d. binary random variables, the code bits ![]() are also modeled as random variables whose properties depend on the structure of
are also modeled as random variables whose properties depend on the structure of ![]() . To get insight into the probabilistic model of the code bits, we will need some simple relationships, which we define in the following.
. To get insight into the probabilistic model of the code bits, we will need some simple relationships, which we define in the following.
The next theorem shows conditions on the matrix ![]() so that the code bits are i.u.d.. We assume therein that the columns of
so that the code bits are i.u.d.. We assume therein that the columns of ![]() are linearly independent, which means that for any
are linearly independent, which means that for any ![]() with
with ![]() we have
we have ![]() .
.
If a matrix has fewer rows than columns, its columns cannot be linearly independent. Consequently, for any ![]() , the generator matrix
, the generator matrix ![]() never satisfies this condition, and thus, the output bits
never satisfies this condition, and thus, the output bits ![]() should be modeled as mutually dependent random variables. On the other hand, a subset of code bits can be independent if a subset of the columns of
should be modeled as mutually dependent random variables. On the other hand, a subset of code bits can be independent if a subset of the columns of ![]() are linearly independent. In other words,
are linearly independent. In other words,
can be mutually independent provided that ![]() has linearly independent columns, where
has linearly independent columns, where ![]() contains a subset of the columns of
contains a subset of the columns of ![]() . In Section 2.6.2, we will explain how to select the code bits to guarantee their independence for the particular case of CENCs.
. In Section 2.6.2, we will explain how to select the code bits to guarantee their independence for the particular case of CENCs.
2.6.1 Convolutional Codes
We use the name convolutional codes to denote the codes obtained using CENCs. We focus on the so-called feedforward CENCs, where the sequence of input bits ![]() is reorganized into
is reorganized into ![]() sequences
sequences ![]() so that
so that ![]() . At each discrete-time instant
. At each discrete-time instant ![]() , the information bits
, the information bits ![]() are fed to the CENC shown in Fig. 2.19. The output of the CENC is fully determined by
are fed to the CENC shown in Fig. 2.19. The output of the CENC is fully determined by ![]() shift registers and the way the input sequences are connected (through the registers) to its outputs (see Fig. 2.20 for an example). We denote the length of the
shift registers and the way the input sequences are connected (through the registers) to its outputs (see Fig. 2.20 for an example). We denote the length of the ![]() th shift register by
th shift register by ![]() , with
, with ![]() , the overall constraint length by
, the overall constraint length by ![]() , and the number of states by
, and the number of states by ![]() . The rate of such encoder is given by
. The rate of such encoder is given by ![]() .
.

Figure 2.19 The encoder ENC in Fig. 2.7 can be a binary CENC with rate 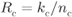

Figure 2.20 Rate  CENC with encoder matrix given by (2.92)
CENC with encoder matrix given by (2.92)
A CENC is fully determined by the connection between the input and output bits, which is defined by the CENC matrix
where the binary vector ![]() contains the convolution coefficients relating the input bits
contains the convolution coefficients relating the input bits ![]() and the output bits
and the output bits ![]() , i.e.,
, i.e.,
where ![]() and
and ![]() , with
, with ![]()
![]() .
.
It is customary to treat the vectors ![]() in (2.89) as the binary representation of a number (with
in (2.89) as the binary representation of a number (with ![]() being the MSB) given in decimal or (most often) in octal notation, as we do in the following example.
being the MSB) given in decimal or (most often) in octal notation, as we do in the following example.
Usually, the design of CENCs relies on a criteria related to the performance of the codes for a particular transmission model. Quite often, as we will also do in Example 3.3, an implicit assumption of binary modulation appears. In such a case, the parameter of the CENC determining the performance is its free Hamming distance (FHD), which is defined as
In general, having defined an optimization criterion, “good” CENCs can be found by an exhaustive numerical search. For example, given the rate ![]() and
and ![]() , maximum free Hamming distance (MFHD) CENCs can be found and tabulated by searching over the CENC universe
, maximum free Hamming distance (MFHD) CENCs can be found and tabulated by searching over the CENC universe ![]() , which is the set of all binary matrices
, which is the set of all binary matrices ![]() . Additional constraints are often imposed, e.g., catastrophic encoders8 are avoided, or we may require the outputs
. Additional constraints are often imposed, e.g., catastrophic encoders8 are avoided, or we may require the outputs ![]() to be u.d. (see Section 2.6.2). The search criterion can be further refined to take into account not only the MFHD but also the code's weight distribution (WD)
to be u.d. (see Section 2.6.2). The search criterion can be further refined to take into account not only the MFHD but also the code's weight distribution (WD) ![]() or its input-dependent weight distribution (IWD)
or its input-dependent weight distribution (IWD) ![]() .9 This is the idea behind the so-called optimal distance spectrum (ODS) CENCs which consider distances
.9 This is the idea behind the so-called optimal distance spectrum (ODS) CENCs which consider distances ![]() ,
, ![]() as well as the frequency of occurrence of events associated with each of these distances.
as well as the frequency of occurrence of events associated with each of these distances.
In Table 2.1, we show the ODS CENCs for ![]() and
and ![]() for different values of
for different values of ![]() . In this table, we also show the FHD
. In this table, we also show the FHD ![]() of each encoder and the total input HW of sequences that generate codewords with HW
of each encoder and the total input HW of sequences that generate codewords with HW![]() .
.
Table 2.1 ![]() and
and ![]() ODS CENCs for different values of
ODS CENCs for different values of ![]() . The table shows the encoder
. The table shows the encoder ![]() , the FHD
, the FHD ![]() , the first element of the WD
, the first element of the WD ![]() , and the first element of the IWD
, and the first element of the IWD ![]()
| 2 | 5 | 1 | 1 | 8 | 2 | 3 | ||
| 3 | 6 | 1 | 2 | 10 | 3 | 6 | ||
| 4 | 7 | 2 | 4 | 12 | 5 | 12 | ||
| 5 | 8 | 1 | 2 | 13 | 1 | 1 | ||
| 6 | 10 | 11 | 36 | 15 | 3 | 7 | ||
| 7 | 10 | 1 | 2 | 16 | 1 | 1 | ||
| 8 | 12 | 11 | 33 | 18 | 1 | 2 | ||
| 9 | 12 | 1 | 2 | 20 | 3 | 6 | ||
2.6.2 Modeling the Code Bits in Convolutional Encoders
Let ![]() be the binary random vector modeling the CENC's output bits
be the binary random vector modeling the CENC's output bits ![]() at time
at time ![]() . From Theorem 2.25, we conclude that for CENCs defined by
. From Theorem 2.25, we conclude that for CENCs defined by ![]() with linearly independent columns and for i.u.d. information bits, the binary vectors
with linearly independent columns and for i.u.d. information bits, the binary vectors ![]() are i.u.d., i.e.,
are i.u.d., i.e., ![]() . This property will be used later to analyze the ML receiver for trellis encoders, where the code bits are directly connected to the mapper, and thus, the fact of having i.u.d. bits
. This property will be used later to analyze the ML receiver for trellis encoders, where the code bits are directly connected to the mapper, and thus, the fact of having i.u.d. bits ![]() directly translates into i.u.d. symbols
directly translates into i.u.d. symbols ![]() as well.
as well.
Let us have a look at the case of BICM. As the interleaver is present between the encoder and the mapper, the bits ![]() are the same as the bits
are the same as the bits ![]() taken from the output of the encoder at different time instants
taken from the output of the encoder at different time instants ![]() and from different encoder's outputs
and from different encoder's outputs ![]() . In what follows, we try to answer the following question: can we guarantee the independence of the bits
. In what follows, we try to answer the following question: can we guarantee the independence of the bits ![]() in BICM? In particular, we will analyze the conventionally assumed independence of the bits in (2.72) for the particular case of CCs.
in BICM? In particular, we will analyze the conventionally assumed independence of the bits in (2.72) for the particular case of CCs.
Theorem 2.27 guarantees that, regardless of the memory ![]() , code bits taken at different time instants are i.u.d., even if the separation is only one time instant. The implication of this for BICM is that the input bits to the mapper will be i.u.d. if they correspond to code bits obtained from the encoder at different time instants. In other words, to guarantee the independence of the bits
, code bits taken at different time instants are i.u.d., even if the separation is only one time instant. The implication of this for BICM is that the input bits to the mapper will be i.u.d. if they correspond to code bits obtained from the encoder at different time instants. In other words, to guarantee the independence of the bits ![]() at the input of the mapper, it is enough to use
at the input of the mapper, it is enough to use ![]() code bits taken at different time instants
code bits taken at different time instants ![]() for any
for any ![]() . This condition is typically guaranteed by an appropriately designed interleaver or by the assumption of using a quasirandom interleaving, in which case, this condition is violated a relatively small number of times. For more details about this, see Section 2.7.
. This condition is typically guaranteed by an appropriately designed interleaver or by the assumption of using a quasirandom interleaving, in which case, this condition is violated a relatively small number of times. For more details about this, see Section 2.7.
For simplicity, Theorem 2.27 was given for ![]() . The following corollary generalizes Theorem 2.27 to any
. The following corollary generalizes Theorem 2.27 to any ![]() . Its proof is not included; however, it follows similar lines to the one used for Theorem 2.27.
. Its proof is not included; however, it follows similar lines to the one used for Theorem 2.27.
To clarify the conditions (2.96) and (2.97) in Corollary 2.29, consider the matrix of the CENC in Example 2.26 (![]() ) given by (2.91). In this case, we have
) given by (2.91). In this case, we have ![]() ,
, ![]() , and
, and ![]() , which corresponds to (2.96) for
, which corresponds to (2.96) for ![]() . The three relevant pairs of bits in this case are rows one and three in (2.91). Similarly, the condition in (2.97) gives
. The three relevant pairs of bits in this case are rows one and three in (2.91). Similarly, the condition in (2.97) gives ![]() ,
, ![]() , and
, and ![]() , which corresponds to rows two and six in (2.91).
, which corresponds to rows two and six in (2.91).
2.6.3 Turbo Codes
The TENC originally proposed in 1993 is based on two parallel concatenated convolutional encoders (PCCENCs) separated by an interleaver as we show in Fig. 2.21. The encoder produces a sequence of systematic bits ![]() , and two sequences of code (parity) bits
, and two sequences of code (parity) bits ![]() and
and ![]() . The latter is obtained by convolutionally encoding the interleaved sequence
. The latter is obtained by convolutionally encoding the interleaved sequence ![]() (interleaved via
(interleaved via ![]() ). At the receiver's side, the decoders of each CENC exchange information in an iterative manner. The iterations stop after a predefined number of iterations or when some stopping criterion is met. The encoder's interleaver is denoted by
). At the receiver's side, the decoders of each CENC exchange information in an iterative manner. The iterations stop after a predefined number of iterations or when some stopping criterion is met. The encoder's interleaver is denoted by ![]() to emphasize that it is different from the interleaver
to emphasize that it is different from the interleaver ![]() used in BICM transmitters between the mapper and the encoder.
used in BICM transmitters between the mapper and the encoder.

Figure 2.21 PCCENCs of rate  . To increase the rate
. To increase the rate  , some of the parity bits are removed (punctured)
, some of the parity bits are removed (punctured)

Figure 2.22 PCCENCs using two identical recursive systematic CENCs of rate 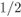 . The overall code rate is
. The overall code rate is 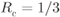 . To increase the rate, puncturing of nonsystematic bits is done most often but, in general, systematic bits can also be punctured
. To increase the rate, puncturing of nonsystematic bits is done most often but, in general, systematic bits can also be punctured


