Chapter 12

Game Theory: Fun Only if You Win

In This Chapter

Playing to win

Taking turns

Playing forever

Losing by winning with prisoner’s dilemma

Winning by losing through preemptive strategies

Committing with credibility

Finally, some fun. You get to play games, and you’ve probably heard the saying, “It’s not whether you win or lose; it’s how you play the game.” A critical point for business that this quote misses is how you play the game determines whether you win or lose. And in business, whether you win — make profit — or lose — incur losses — means everything.

Strategic decision-making occurs when the game’s outcomes depend on the choices made by different players. Because the outcomes are interdependent, players must consider how rivals respond to their decisions. Competition in these situations leads to mutual interdependence with conflict. The complexity of the resulting environment requires decision-making rules. Game theory provides a framework for making the decisions. Game theory’s goal is to provide rules that enable you to correctly anticipate a rival’s decision.

A great example of game theory is the board game Monopoly. Monopoly involves multiple decision-makers or players. The decisions each player makes influence the game’s outcome. If I build a hotel on St. James Place and you land on it, you owe me $950. On the other hand, if you land on St. James Place when it has no house or hotel, your rent is only $14.

This chapter examines how decisions are made in game theory. I start by describing a game’s possible structure. I then examine how decisions are made given the game’s structure. A player chooses an action based on the competitor’s decision and information the player possesses. I note that players never choose a dominated action because a better choice is always available through either a pure or mixed strategy. Next, I examine games that result in a lose-lose outcome because of the prisoner’s dilemma. I examine games involving sequences of decisions to determine whether moving first is always desirable. The chapter concludes with some special situations applying game theory, including collusion and preemptive strategies. By understanding how to play a variety of games, game theory helps improve your ability to influence the strategic environment in a number of situations ranging from oligopolistic markets to auctions. Wherever outcomes are interdependent — that is, the outcome is jointly determined by the decisions made by two or more players — you should consider using game theory.

Winning Is Everything

A game is a competitive situation where two or more players pursue their own goals — such as profit maximization or cost minimization — with no single player able to dictate the game’s outcome. Being competitive simply means that you play to win, and in business decision-making, winning means you make profit, and lots of it.

The mutual interdependence among firms in an oligopolistic market (see Chapter 11) resembles a game, and, thus, decision-makers are likely to find game theory useful in understanding these markets.

Players are the decision-makers. Players generally start with a given amount of resources. For example, in the board game of Monopoly, players start with two $500 bills, two $100 bills, two $50 bills, six $20 bills, five $10 bills, five $5 bills, and five $1 bills. In the business world, players may start with as little as their own labor and entrepreneurial abilities. Players must then decide how to use those resources.

Structuring the Game

A game is composed of rules, actions, and payoffs. The game’s structure plays a crucial role in determining the ultimate outcome.

Making rules for the game

Rules of the game describe how the game is played. Rules of the game include whose turn it is, how resources can be employed, technological constraints, what government regulations permit, and so on. Like in Monopoly, the rule book can be quite lengthy and can include things like how to mortgage property and when to pay taxes.

Actions

Actions are the choices a player can make. In Monopoly, it may be the decision to buy or not to buy Boardwalk when you land on it. Players need to consider possible actions when making a decision — not only their own but also the possible actions of their rivals. If you don’t buy Boardwalk, who might?

The actions chosen by all players ultimately determine the game’s outcome. Thus, before starting the game, you need to recognize who all the players are, and the possible decisions they can make. Sound decisions require that you completely specify the actions you can take and what rivals do given each of your possible actions. Therefore, the game’s structure must recognize how players respond to all possible circumstances at each stage in the game.

Determining the payoff

Payoffs represent the outcome or returns of the game. The payoff depends not only on the decisions you make, but also on the decisions your rivals make. Thus, payoffs are the result of a combination of actions indicating the players’ strategic interdependence.

A payoff table summarizes the various combinations of outcomes for all players and all possible actions. Typically, players are assumed to be rational when they make decisions. Players subscribe to the philosophy “Don’t harm thyself.” This philosophy is a sound assumption to make in the profit-motivated business world.

Identifying whose turn it is in decision-making

The game theory framework requires knowing how players take turns while playing the game. In tic-tac-toe, the player who moves first has a much higher probability of winning because that player gets to move five times in the game while the player moving second gets only four possible moves. Similarly, in chess, numerous studies have shown that white, the color that always moves first, wins more than fifty percent of the games.

Similarly, how firms take turns in oligopoly influences the outcome. In Chapter 11’s presentation of the Stackelberg model, the firm that is the leader and chooses first produces a lot more output than the firm that chooses second. Or if Coca-Cola comes out with a new advertising campaign, it might be able to steal customers from Pepsi. Similarly, the airline that cuts fares can increase the number of passengers it carries until rivals have an opportunity to respond.

Thus the order in which players select is crucial in determining the game’s outcome. Check out the next section for details on how to make decisions in various game scenarios.

Making Decisions

The following sections outline how decisions are made in the following scenarios:

Simultaneous-move games: Rock-paper-scissors is a simultaneous-move game. In the game, players make their decisions at the same time. A simultaneous-move game also exists if you make decisions without knowing what the other players have decided.

Sequential-move games: Tic-tac-toe and chess are examples of sequential games — one player chooses first, and then the other player gets to respond. In sequential games, everybody except the player who moves first gets to observe their rivals’ decisions before making their own decision.

One-shot games: The game is played only once. The game isn’t repeated among players. A duel is an example of a one-shot game that’s also a sequential-move game. And as this example illustrates, it can be very important to play even one-shot games well.

Repeated games: Players know the game is played over and over again. An infinitely-repeated game never ends. The baseball World Series is a repeated game with teams playing at least four and up to seven times. On the other hand, professional football’s Super Bowl is another example of a one-shot game.

Simultaneous-move, one-shot games

In these games, players make decisions at the same time or, at the very least, they don’t know their rival’s decision prior to making their own. In addition, the game is played only once.

Assume that two players, you and me, are trying to determine whether or not to increase our sales by expanding our business to a second location in a neighboring town. Figure 12-1 illustrates the payoff table associated with our possible decision combinations.

My decisions are represented on the left side of the table. The top row represents my choice to expand, and the bottom row is my choice to not expand. Your decisions appear across the top of the payoff table — the left column represents your choice to expand and the right column is your choice to not expand.

Figure 12-1: Payoff table with dominant actions.

Each cell in the payoff table presents the results of the actions you and I take. In this example, I assume the payoffs are the business’s monthly profit. Thus, if I decide to expand and you decide to expand, the resulting payoffs are contained in the upper-left cell of the payoff table. The cell indicates that my monthly profit is $2,400 and your monthly profit is $3,500. If, instead, I decide to not expand while you decide to expand, my profit is $1,400, while your profit is $5,000.

Identifying dominant actions

A dominant action is an action whose payoff is always highest, regardless of the action chosen by your opponent. In Figure 12-1, your dominant action is to expand. To understand why, note the following:

If I decide to expand, you read across the top row, and your possible payoffs are $3,500 if you also expand or $3,000 if you don’t expand. You should expand because it leads to a better payoff.

If I decide to not expand, you read across the bottom row, and your possible payoffs are $5,000 if you expand or $2,500 if you don’t expand. Again, you should expand.

No matter what I choose, you always get a better payoff — higher profit — if you expand. To expand is a dominant action for you because its payoff is always better than not expanding.

A similar situation exists for me:

If you decide to expand, I read down the left column, and my possible payoffs are $2,400 if I also expand or $1,400 if I don’t expand. I should expand because it leads to a better payoff.

If you decide to not expand, I read down the right column, and my possible payoffs are $4,000 if I expand or $2,000 if I don’t expand. Again, I should expand.

To expand is a dominant action for me because no matter what you choose, I get a better payoff — higher profit — by deciding to expand instead of not expanding.

You should never choose an action that is dominated.

So, how does our game turn out? Because the dominant action for both of us is to expand, we both choose that action. I receive $2,400 in monthly profit, and you receive $3,500 in monthly profit. Our combined profit is $5,900. Interestingly, this payoff is not the best combined payoff for us. If I expand and you don’t expand, our combined payoff would be $7,000 — $4,000 for me and $3,000 for you. This higher combined payoff provides an incentive for us to merge.

Considering the maxi-min rule and reaching the Nash equilibrium

The game in the previous section is fairly easy because we both have only two actions and one of them is a dominant action. Figure 12-2 illustrates a more complicated game because each player now has three possible actions — reduce fares, charge the same fares, or raise fares. This game is still a simultaneous-move, one-shot game, so each player gets to make a single decision without knowing what the other player decides. Figure 12-2 indicates the resulting annual profit in millions of dollars based upon the combination of actions each airline takes.

In Figure 12-2, neither airline has a dominant action. For Global Airline, none of the possible decisions regarding fares always has a higher payoff when compared to another fare decision. When comparing the columns for reduce fares and same fares, sometimes reduce fares has higher payoff — for example, when International charges the same fare, Global’s reduce fare yields $38 and Global’s same fare yields only $35. But sometimes, same fares has a higher payoff — for example, when International reduces fares, Global’s same fare has $32 and reduce fare has only $18. Similarly, when comparing reduce fares to raise fares and same fares to raise fares, Global never has a situation where one action always has a higher payoff compared to the other action. The same situation exists for International Airline.

Figure 12-2: Payoff table for three-action game.

The maxi min rule

Because the situation in Figure 12-2 can’t be simplified by dominant actions, rules are necessary to guide decision-making. One possible rule is called the maxi min rule. When using the maxi min decision rule, firms look at the worst possible outcome for each action, and then choose the action whose worst possible outcome is best — in other words, the firm maximizes the minimum gain. In oligopolistic markets, this rule can seem like a reasonable strategy for a firm to use, because its rivals are likely to pursue actions that result in the worst possible outcome for the firm.

If International Airline applies the maxi min rule in Figure 12-2, its goal is to choose the action that results in the best possible worst outcome, or to maximize the minimum payoff. To apply this rule, International takes the following steps.

1. International determines its worst possible payoff if it reduces fares.

The worst possible payoff if International reduces fares is $27 that occurs if Global also reduces fares.

2. International determines its worst possible payoff if it charges the same fare.

The worst possible payoff in this situation is $25 that occurs if Global raises fares.

3. International determines its worst possible payoff if it raises fares.

The worst outcome is $29 that occurs if Global reduces fares.

4. International applies the maxi-min rule and raises fares.

International Airline raises fares because it results in the best possible worst outcome — $29 is better than either $27 or $25.

The maxi min rule is a very conservative strategy. It has a major problem because it looks only at the worst possible outcome. You don’t even consider other possible outcomes. So, applying this rule means you would probably never invest in a business. Investing in a business means you might lose money. If you just hold onto your money, you won’t lose it.

Another problem with the maxi min strategy is you ignore what your rival may choose. A better way to make decisions in game theory is to anticipate what your rival may do. For example, in playing the board game Monopoly, if your opponent already owns the orange properties of Tennessee Avenue and New York Avenue, when you land on St. James Place, you should buy it to prevent your opponent from getting a monopoly. You take into account that your opponent will certainly buy St. James if she lands on it.

What happens if International Airline anticipates Global’s decision. In this case, if International reduces fares, Global charges the same fare, because that has the highest payoff — $32. If International charges the same fare, Global reduces fares to earn $38. If International raises fares, Global also raises fares to receive $41. These cells are marked with a “G” in Figure 12-2.

Alternatively, what happens if Global Airline anticipates International’s decision. In this case, if Global reduces fares, International charges the same fare, because that has the highest payoff — $36. If Global charges the same fare, International charges the same fare to earn $42. If Global raises fares, International reduces fares to receive $44. These cells are marked with a “I” in Figure 12-2.

The Nash equilibrium

The game illustrated in Figure 12-2 ultimately results in International Airline deciding to charge the same fare and Global Airline deciding to reduce fares. This outcome is called a Nash equilibrium. A Nash equilibrium exists when no player can improve his or her payoff by unilaterally changing his or her action given the actions chosen by other players. In order to reach a Nash equilibrium, each player chooses the action that maximizes the payoff conditional on others doing the same.

So, in Figure 12-2, if International Airline changes its decision to either reduce or raise fares given that Global Airline has reduced fares, its profit is less than the $36 it receives from charging the same fare. Similarly, if Global Airline changes its decision to either charge the same fare or raise fares, its profit is less than the $38 it receives from reducing fares. International and Global airlines are in a Nash equilibrium because neither airline can improve its payoff given the decision made by the other player. The Nash equilibrium is indicated by the cell with I and G.

To find where a Nash equilibrium exists, simply note the firm’s highest payoff cell given each decision its rival can make. Do the same thing with the rival. A cell that has the highest payoff for both firms is a Nash equilibrium.

Losing because of the prisoner’s dilemma

A prisoner’s dilemma refers to a game where players choose something less than the optimal combined actions.

Figure 12-3 presents the payoff table of monthly profits for two competing restaurants — Bob’s Barbecue and Clara’s Cafeteria. Both Bob and Clara are deciding whether or not to expand their menus, and the resulting payoff depends upon not only the decision each of them makes but also on the decision their rival makes. In determining the ultimate payoff, you should first identify whether or not either restaurant has a dominant action. To identify any dominant actions and determine the ultimate payoff, you take the following steps:

Figure 12-3: A prisoner’s dilemma.

1. Determine how Clara responds to Bob’s decisions.

If Bob introduces a new menu item, Clara should also introduce a new menu item because her monthly profit is $1,700 instead of $1,400. If Bob doesn’t introduce a new menu item, Clara should introduce a new menu item because her monthly profit is $3,000 instead of $2,000. Introducing a new menu item is a dominant action for Clara because its payoff is always higher than not introducing a new menu item.

2. Determine how Bob responds to Clara’s decisions.

If Clara introduces a new menu item, Bob should also introduce a new menu item because his monthly profit is $1,600 instead of $1,000. If Clara doesn’t introduce a new menu item, Bob should introduce a new menu item because his monthly profit is $2,400 instead of $2,100. Introducing a new menu item is a dominant action for Bob because its payoff is always higher than not introducing a new menu item.

3. Determine the ultimate payoff.

Because introducing a new menu item is the dominant action for both Bob and Clara, the ultimate payoff is in the upper left cell of the payoff table. Bob’s Barbecue receives $1,600 profit and Clara’s Cafeteria receives $1,700 profit.

This example leads to a prisoner’s dilemma because Bob and Clara ultimately receive profits that are less than optimal. If both Bob and Clara decide not to introduce a new menu item, both receive more profit — $2,100 for Bob and $2,000 for Clara. But Bob and Clara don’t do that, because in that situation, each could make more profit by introducing a new menu item. If Bob introduces a new menu item, his profit goes to $2,400, but Clara’s profit goes down to $1,400. So, Clara is “forced” to also introduce a new menu item to get her profit from $1,400 to $1,700, but Bob’s profit goes down to $1,600. Similarly, if Clara introduces a new menu item, her profit goes to $3,000, but Bob’s profit goes down to $1,000. So, Bob is “forced” to also introduce a new menu item to get his profit from $1,000 to $1,600, but then Clara’s profit goes down to $1,700. By acting out of self interest, both Bob and Clara end up with smaller profit, but ignoring what their rival does is even worse.

With a prisoner’s dilemma, players chose the action that best serves their own interests. However, the result of this behavior is a combined payoff that’s less than optimal.

Sequential-move, one-shot games

In many games, one player chooses before another, and it’s difficult to know who has the advantage. As I note earlier in this chapter, in chess, if you move first, you have a greater probability of winning. On the other hand, in business situations, if you move first, your rival may be able to neutralize your decision by moving second. You need to develop a decision-making rule that helps you anticipate your rival’s decision.

Decision-makers use backward induction in sequential games. Backward induction means that you develop your decision by looking at the future, or at how the game ends. Consider the decision tree in Figure 12-4. Two car dealers, Cathy’s Cars and Otto’s Autos, must decide whether to raise, lower, or charge the same price on their used cars. Because of her leadership position in the market, Cathy’s Cars chooses her used car price first, and then Otto’s Autos follows. When establishing her price, Cathy needs to consider how Otto responds by using backward induction. Using backward induction requires the following steps. Decision-makers start at the end of the game. The player making the last decision chooses the decision that has the greatest payoff. As a result, the player making a decision in the step before the last decision takes into account the likely decision in the last step when making her decision. Decision-makers continue working backward from the last decision, taking into account the likely decision made at each step in the sequence, until the first step — the initial decision step — is reached. Figure 12-4 illustrates the backward induction process.

Figure 12-4: Backward induction.

Figure 12-4 summarizes the various outcomes that are possible in the situation. The far left starts with Cathy’s possible choices — she can raise price, charge the same price, or lower price. In the middle, Otto’s choices are portrayed for each possible choice Cathy can make. At the far right are the annual profits each dealer receives given their combined choices. For example, if Cathy lowers price, follow the lower branch from Cathy’s Cars to Otto’s Autos. If Otto charges the same price, follow the middle branch to the outcome — $92,000 profit for Cathy and $68,000 profit for Otto. Thus, when making her decision, Cathy needs to consider how Otto responds.

1. If Cathy raises price, Otto charges the same price to earn $94,000.

Otto charges the same price because $94,000 is a higher profit for Otto than $84,000 if he raises price or $73,000 if he lowers price. As a result, Cathy’s profit is $66,000.

2. If Cathy charges the same price, Otto lowers price to earn $87,000.

Otto lowers price because $87,000 is a higher profit than $79,000 if Otto raises price or $76,000 if he charges the same price. Cathy’s profit is $71,000 — the result of her charging the same price and Otto lowering price.

3. If Cathy lowers price, Otto charges the same price to earn $68,000.

Otto charges the same price because $68,000 is a higher profit than $25,000 if Otto raises price or $63,000 if he lowers price. Cathy’s profit is $92,000.

4. Cathy’s decision is to lower price.

When Cathy lowers her price, Otto charges the same price, resulting in $92,000 profit for Cathy and $68,000 profit for Otto. The $92,000 profit for Cathy is the best she can expect after Otto makes his choice. As indicated in Step 1, if Cathy raises price she ultimately receives $66,000 in profit and if she charges the same price, she receives $71,000 in profit as indicated in Step 2.

By using backward induction to anticipate Otto’s response to her decision, Cathy is able to choose the best possible action.

Infinitely repeated games

One-shot games provide an excellent introduction to game theory; however, they can lead to mistaken conclusions when applied too rigidly to the business world. A crucial element missing in one-shot games is time. The business world is characterized by numerous decisions made over an extended period of time. A payoff is associated with each decision, and the players also have memory of past decisions. For all practical purposes, the business time horizon is infinite — the game is never-ending. The result is an infinitely repeated game.

In infinitely repeated games, you need to take into account not only how your rival plays this round, but also how this round of the game influences future rounds. Another factor you must consider in infinitely repeated games is the time value of money. A dollar received today is worth more than a dollar received one year from now, because the dollar received today can earn interest. Thus, future payoffs must be adjusted by using the present value calculation I describe in Chapter 1.

The typical strategy used in an infinitely repeated game is the trigger strategy. A trigger strategy is contingent on past play — a player takes the same action until another player takes an action that triggers a change in the first player’s action. An example of a trigger strategy used in games involving a prisoner’s dilemma is tit-for-tat. When you use a tit-for-tat strategy, you start by assuming players cooperate. In any subsequent round, you do whatever your rival did in the previous round. Thus, if your rival cheated on an understanding in the last round, you cheat this round. If your rival cooperated in the last round, you cooperate this round. A tit-for-tat strategy tends to lead to cooperation because it punishes cheaters in the next round. In addition, it forgives cheaters if they subsequently decide to cooperate. One requirement of the tit-for-tat strategy is that the players are stable. The players remember how the game was played in the previous period. New players can upset the necessary balance by not having the required memory of past behavior.

In this example, I talk about two railroads you may recognize from the board game Monopoly — the Pennsylvania Railroad and the B & O Railroad. Here, they’re competing for traffic between the same cities. The railroads can either cheat on one another and charge low prices for freight, or they can cooperate and charge high prices. I show the resulting payoff table of annual profits in Figure 12-5.

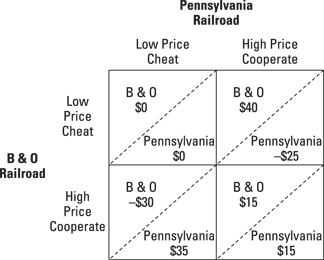
Figure 12-5: An infinitely repeated game.

In this payoff table, both railroads have a dominant action — to charge a low price. As a result, they both earn $0. This result is yet another prisoner’s dilemma.

If these railroads play the game a long time, they both recognize that cooperating by charging a high price allows both to earn $15 million each and every year. Cheating by charging a low price may lead to a large payoff one year, but the cost associated with having your rival cheat in the next year is very high. Consider what happens in a tit-for-tat strategy:

1. If the B & O Railroad charges a high price, and the Pennsylvania Railroad cheats and charges a low price, B & O’s losses are $30 million and Pennsylvania’s profit is $35 million.

2. Following a tit-for-tat strategy, the B & O Railroad charges a low price the next year, and the Pennsylvania Railroad continues to charge a low price.

The railroads are locked into a situation of zero profit forever, because the B & O Railroad continues to charge the low price that the Pennsylvania Railroad charged the previous year. The railroads are in a prisoner’s dilemma.

3. Following a tit-for-tat strategy, the B & O charges a low price the next year and the Pennsylvania Railroad charges a high price.

The B & O Railroad earns $40 million in profit and Pennsylvania loses $25 million. But now the game can return to cooperation. The B & O forgives the Pennsylvania Railroad for cheating in the first round and in future rounds, each railroad earns $15 million.

In some sense, the Pennsylvania Railroad has to accept punishment for cheating in the first place. But accepting that punishment one year leads to a situation where both railroads return to $15 million annual profit. If the railroads continue to cheat by charging a low price, each will recognize that cooperation does not pay, and they will be forever locked into charging a low price and receiving zero profit.

In this infinite game, both railroads make more profit if they cooperate the entire time and never fall into a tit-for-tat strategy.

If you have an infinite time horizon, the present value of a constant stream of future net revenue equals

where π is the net revenue earned each year and i is the interest rate.

In the previous example, if the B & O and Pennsylvania railroads cooperate, they each earn $15 million annual profit. If the B & O Railroad has an infinite time horizon, the present value of $15 million annual profit at a 5 percent interest rate is

or $315 million.

Playing Well

How you play the game determines whether you win or lose, so you want to play the game well. Playing any game well requires you to consider how your rival responds to your decisions. But as the next section on preempting rivals illustrates, you can also change your rival’s behavior if you play well.

Preempting rivals

You’ve developed a highly-regarded bike shop in the local community. A larger neighboring community has a bike shop owned by a rival. Your rival’s bike shop is larger and you fear that the rival may be considering entering your market. You need a strategy that enables you to preempt your rival. This is an obvious game theory situation where you must take into account your rival’s actions.

Assume the possible scenarios are represented by the decision trees in Figure 12-6 with the payoff being annual profit. The upper panel describes the current situation. If your rival expands, you can either expand or not expand. Using backward induction, your rival takes the following steps:

1. If your rival doesn’t expand, the status quo continues.

The status quo is represented by the lower branch on the decision tree. If your rival doesn’t expand, you won’t do anything — there are no branches for your decision — and the profits are $100,000 for your rival and $80,000 for you.

2. If your rival expands, you don’t expand.

If your rival expands, you don’t expand because if you expand your profits are $20,000 versus if you don’t expand, your profits are $25,000.

Figure 12-6: Preemptive strategy.

3. Your rival decides to expand by using backward induction.

Given you don’t expand, your rival earns $150,000 by expanding into your community, while the rival earns only $100,000 if it doesn’t expand. And the bad news for you is your profit is only $25,000. You aren’t likely to enjoy this game, so how can you change it?

4. You engage in a preemptive strategy by renting a store location in your rival’s community for $10,000 a year.

This is how much you would have to pay if you decide to expand into your rival’s community. This changes the decision tree by lowering your profit by $10,000 in every situation you don’t expand because of the added expense you incur. It doesn’t change your expense if you do expand — you need the store. So in the decision tree in the lower panel, your profit for when both you and your rival expand doesn’t change — it remains $20,000. Your profit for when your rival expands but you don’t expand goes down by $10,000 from $25,000 to $15,000 because of the rent you pay on the unoccupied store front. Similarly, your profit if your rival decides not to expand goes down by $10,000 for the unoccupied store front, from $80,000 to $70,000.

5. Your rival uses backward induction.

If your rival doesn’t expand, the status quo continues. The profits are $100,000 for your rival and now only $70,000 for you.

6. If your rival expands, you also expand.

If you don’t expand, your profit is $15,000. If you expand, your profit is $20,000.

7. If both you and your rival expand, your rival earns $70,000 profit.

This combines both decisions to expand.

8. Your rival decides not to expand.

By not expanding, your rival earns $100,000 profit as opposed to only $70,000 profit if your rival expands.

Your preemptive strategy changes your rival’s behavior. Not taking the preemptive strategy results in you earning $25,000 profit. By spending $10,000 to rent a store front you never plan to use, you increase your profit to $70,000.

Working together through collusion

A logical question implied by the prisoner’s dilemma is: Why don’t both firms choose the combination of actions that yields the highest combined payoff? The answer is that they often do. Because oligopolistic markets are characterized by a small number of firms, they recognize their mutual interdependence. Such conditions favor collusion and the formation of cartels. However, as I note in Chapter 18, antitrust laws in the United States make most forms of collusion illegal.

Figure 12-7 again portrays the prisoner’s dilemma experienced by Bob’s Barbecue and Clara’s Cafeteria (see the earlier section “Losing because of the prisoner’s dilemma”). As a result of the prisoner’s dilemma, Bob and Clara end up receiving $1,600 and $1,700 in monthly profit, respectively. However, if Bob and Clara collude, they both agree not to introduce a new item. In that case, Bob’s profit is $2,100 and Clara’s profit is $2,000. Both restaurants are better off.

This illustration also indicates why collusion often breaks down. Both Bob and Clara have an incentive to cheat on the collusive agreement. If Bob can secretly introduce an “off-menu” new item, he increases his profit from $2,100 to $2,400. Obviously, when Clara realizes Bob is cheating on their collusive agreement, Clara will also introduce a new menu item, resulting in the prisoner’s dilemma outcome. A similar scenario develops if Clara gives in to her incentive to cheat. Nevertheless, methods such as the tit-for-tat strategy (see the “Infinitely repeated games” section earlier in this chapter) can discourage cheating on collusive agreements.

Figure 12-7: Choosing collusion.

Testing commitment

You’ve heard a rumor that if you decide to expand your business into a rival’s territory, the rival will respond by expanding into your territory. Before making your decision on whether or not to expand, you need to determine whether the threat is credible.

A credible commitment requires the commitment’s benefit to exceed its cost. In that case, the commitment is credible because the firm has an incentive to follow through. In the situation of whether or not your rival expands into your territory after you expand into its, the commitment — threat — is credible if the benefit outweighs the cost. Figure 12-8 illustrates this situation.

Your rival says it will expand only if you expand first. You’re concerned about your rival’s threat to expand, because if both firms expand, your profit is only $10,000. You need to use backward induction to test whether or not your rival’s commitment is credible. In Figure 12-8’s decision tree, your decision appears at the far left, because you choose first. You have two possible choices — expand or don’t expand. After you decide, your rival responds. To determine whether your rival’s threat to expand is credible, you take the following steps:

1. Because you’re trying to decide whether to expand, focus on the upper branch of the decision tree that corresponds to expand.

2. If you expand, your rival can expand or not expand.

If your rival chooses to expand, his profit is $25,000. If your rival chooses not to expand, his profit is $40,000. As a result, your rival chooses not to expand for the higher profit.

3. Your rival’s commitment isn’t credible.

If your rival chooses to expand after you expand, its profit is $15,000 less — only $25,000 instead of $40,000 — than if it didn’t expand. Your rival is better off (makes a higher profit) by not expanding even if you choose to expand.

4. You should expand, recognizing that your rival’s commitment isn’t credible.

This example reinforces how fun game theory is. If you look again at Figure 12-8, you quickly see you just had $80,000 worth of fun because the way you play the game determines whether you win or lose.