Chapter 6

Production Magic: Pulling a Rabbit Out of the Hat

In This Chapter

Understanding variable and fixed inputs, and their relationship to time

Defining the relationship between inputs and output

Producing with one variable input

Minimizing costs with multiple inputs

Considering returns to scale

Economics contains a lot of surprising and therefore magical conclusions. For example, you can increase your firm’s revenues sometimes by lowering price and thus selling a lot more or other times by raising price if you sell only a few less. (See Chapter 4 on elasticity.) Similarly, in production, sometimes you’re better off using a lot of machines, what economists call capital, to produce your good, and other times you’re better off using more labor.

The amount you use of an input depends upon how much it costs and how much output it adds. The crucial thing to determine is what input combination minimizes the cost of producing a given quantity of output. And minimizing cost is mandatory if you want to maximize profits. Maximizing profits — now that’s magical.

Producing Hats: Identifying the Types of Inputs and Timely Production

Any good magician needs a hat. That’s where the rabbit comes from. Somebody has to produce the magician’s hat, and I bet the producer wants to make a lot of money or profit. One way for the hat producer to make more profit is to choose inputs that minimize the cost of production. As an aside, I’ll leave the description of rabbit production to somebody else.

Economists call inputs, or resources, factors of production. They are the factors used to produce your product or output.

Here are the four major factors of production:

Labor refers to human effort

Capital refers to machinery, equipment, and factories

Land refers to resources taken from the earth

Entrepreneurial skills refer to skills related to innovation and risk evaluation

As the manager, you have to decide what combination of these inputs minimizes your production cost.

So, you want to produce a hat. You’ll need labor, felt (magicians use old felt top hats), thread, scissors, and a sewing machine. The quantity of some of these inputs can be changed fairly easily (labor), while the quantity of other inputs is harder to change (sewing machines). Economists distinguish between these types of inputs by calling them variable or fixed.

Variable inputs are inputs whose quantities can be readily changed in response to changes in market conditions. Labor is typically a variable input. If you have a huge increase in the demand for felt top hats, working just a little longer, or perhaps hiring another worker, is easy to do.

Fixed inputs are inputs whose quantities can’t be readily changed in response to market conditions. Even if you have a huge change in the demand for felt top hats, it would take a fairly long period of time to adjust the size of the factory where you’re making them in order to add more sewing machines.

Economists also create their own definition of time. Rather than use a clock or calendar like normal people, economists define time based upon whether or not the quantities employed of various inputs can be changed. Thus, instead of using hours, days, and weeks, economists talk about the short run and the long run.

Being limited in the short run

In the short run, some inputs are fixed and some inputs are variable. So, you can adjust some, but not all, of your inputs in order to change the quantity of output produced. With the increased demand for hats, you can change the labor in the short run — labor is a variable input — while you can’t change the size of the factory — the factory is a fixed input.

Looking forward to the long run and life without limits

In the long run, all inputs can be changed and thus are variable. So in the long run, even building an entirely new factory is possible. But the relationship between the long run and your calendar varies from industry to industry. For a restaurant, you can probably start from scratch and have the restaurant open within six months. Thus, the long run in the restaurant industry is six months. For a power company, building a new power plant may take six years or more; thus, the long run is at minimum six years. Because all inputs are variable in the long run, your business can change anything it wants — you have no limits on what you can change.

Defining the Production Function: What Goes in Must Come Out

A production function specifies the relationship that exists between inputs and outputs for a given technology. In general terms, a production function is specified as

where x1 through xn represent the various inputs in the production process, and q represents the quantity of output produced. If you have only two inputs in the production process — labor, L, and capital, K — you write the production function as

The specific function described by a general statement may have many forms. For example,

indicates a linear relationship between both labor and output and capital and output. In this equation, for every one-unit increase in labor, the quantity of output produced increases by two units, while a one-unit increase in capital leads to a five-unit increase in output. Alternatively, the production function may take the form

This commonly used production function is called the Cobb-Douglas function. The Cobb-Douglas production function is widely used because it assumes some degree of substitutability between inputs, but not perfect substitutability. So, labor can be substituted for capital — dishes can be washed by hand at a restaurant or in a dishwasher — but labor is not a perfect substitute for capital.

Starting with Basics by Using Single Input Production Functions

Production functions typically have more than one input; however, in the case of a single input production function, you assume that the quantity employed of only one input can be varied. In other words, you have one variable input and all other inputs in the production process are fixed inputs — and you can’t change the quantity of the fixed inputs.

You’re a farmer trying to decide how much land you’re going to plant in corn and how much you’ll leave for hay. You’ve decided to treat the quantities of labor (you’re the only one working) and machinery employed constant. In this situation, labor and capital (the machinery) are fixed inputs and land is a variable input.

The following equation describes the relationship between the amount of land you use and the quantity of corn produced

Where q is the number of bushels of corn grown and N is the amount of land used.

I know, the 0.9 power looks strange, but trust me, your computer can handle it. Nevertheless, Table 6-1 presents some of the land, output combinations that are possible.

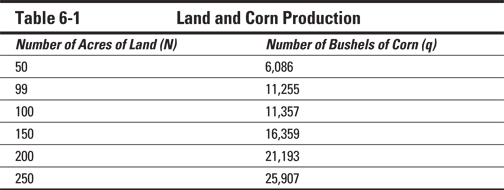
I graph this equation in Figure 6-1.

Figure 6-1: A single input production function.

Distinguishing between average product and marginal product

You can examine the relationship between inputs and output in a number of different ways. You may be concerned with only the total amount of corn grown — what economists call total product. Alternatively, you may be interested in the average quantity of corn produced per acre of land, what farmers call yield, and economists call average product, or you may be interested in how much corn output increases when you plant one more acre, marginal product to economists. Each of these relationships is important, and each offers considerable insight into the production process.

Total product refers to the entire quantity of output produced from a given set of inputs. In the equation, q represents total product. Therefore, if you plant 100 acres of corn, total product equals

or 11,357 bushels of corn produced.

Average product refers to the output per unit of input. For a production function that has a single variable input, average product equals the total product divided by the quantity of input used. Therefore,

If you plant 100 acres of corn, the average product equals

or 113.57 bushels per acre.

Marginal product is the change in total product that occurs when one additional unit of a variable input is employed. In Table 6-1, the marginal product of the 100th acre of land is 102 bushels of corn. The total product for 99 acres is 11,255 bushels, and the total product for 100 acres is 11,357 bushels. Thus, the difference or change between the two is 11,357 – 11,255 or 102 bushels of corn.

Marginal product is also determined with calculus.

To determine marginal product with calculus, take the following steps:

1. Take the derivative of total product with respect to the input. In the example, this is land (N).

2. Substitute in the appropriate value for the input. So, to determine the marginal product of the 100th acre of land, substitute 100 for N and solve (with the help of your computer or calculator).

Thus, if you start at 100 acres, adding another acre of land increases output by 102 bushels.

Diminishing returns

The law of diminishing returns states that ceteris paribus, as the quantity employed of an input increases, eventually a point is reached where the marginal product of an additional unit of that input decreases.

The term ceteris paribus indicates that all other things — for example, the quantities employed of other inputs and technology — are held constant. Therefore, the law of diminishing returns indicates that after some point, additional units of a variable input aren’t as productive as preceding units of the input.

Making Production More Realistic with Multiple Input Production Functions

Although single-input production functions are useful for illustrating many concepts, usually, they’re too simplistic to represent a firm’s production decision. Therefore, it’s useful for you to understand the firm’s employment decision when the quantities employed of two or more inputs are changed. In other words, you’re dealing with two or more variable inputs.

Consider the production function q = f(L,K), which indicates the quantity of output produced is a function of the quantities of labor, L, and capital, K, employed. The specific form of this function may be the following Cobb-Douglas function

Table 6-2 illustrates the relationship between various values for labor and capital and a total product of 3,200 units for this equation.

Examining production isoquants: All input combinations are equal

The relationship between labor, capital, and the quantity of output produced in the previous equation is graphically described by using a production isoquant. A production isoquant shows all possible combinations of two inputs that produce a given quantity of output. Table 6-2 shows various combinations of labor and capital that produce 3,200 units of output.

Figure 6-2 illustrates the production isoquant, labeled q1, derived from Table 6-2 and the equation

In Figure 6-2, the curve labeled q1 represents all combinations of capital and labor that produce 3,200 units of output.

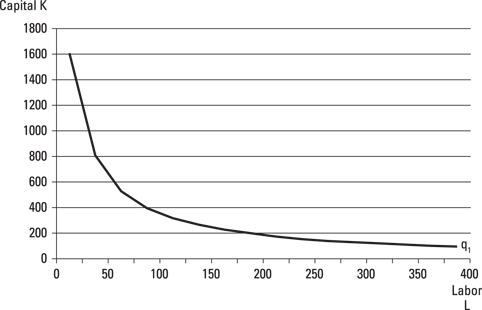
Figure 6-2: This production isoquant shows all combinations of capital and labor that produce 3,200 units of output.

Thinking at the margin one more time

Earlier in this chapter, I define marginal product as the change in total product that occurs given one additional unit of an input. With a production isoquant, the amount of output you gain from using one more unit of labor is exactly offset by the amount of output you lose by using less capital.

Every input combination on the production isoquant produces the same level of output — output is constant. Capital can change by more or less than one unit. What is critical is that total product remains constant as you increase labor and decrease capital.

Knowing the marginal rate of technical substitution

The marginal rate of technical substitution measures the change in the quantity of the input on the vertical axis of the diagram that’s necessary per one-unit change of the input on the horizontal axis of the diagram in order for total product to remain constant.

That’s too technical of a definition, so remember this instead — the marginal rate of technical substitution is simply the production isoquant’s slope. The production isoquant’s slope equals the marginal product of the input on the horizontal axis divided by the marginal product the input on the vertical axis.

Defining isocost curves: All input combinations cost the same

An important factor in your production decision is how much the inputs cost. If an additional worker (unit of labor) costs less than an additional unit of capital, but the worker produces the same quantity of output as the capital, it’s a good deal to hire the additional worker. So, you need to add cost to your decision-making process.

The isocost curve illustrates all possible combinations of two inputs that result in the same level of total cost. The isocost curve is presented as an equation. For a situation with two inputs — labor and capital — the isocost curve’s equation is

In this equation, C is a constant level of cost, pL is the price of labor, L is the quantity of labor employed, pK is the price of capital, and K is the quantity of capital employed.

On a graph, the isocost curve’s slope equals the price of the input on the horizontal axis divided by the price of the vertical axis input.

Assume your total cost is $4,000 a day, and labor costs $20 per hour, and capital costs $5 per machine-hour. Given this information, your isocost curve equation is

Some possible combinations of labor and capital you can employ for a total cost of $4,000 are 50 hours of labor and 600 machine-hours of capital, 100 hours of labor and 400 machine-hours of capital, and 150 hours of labor and 200 machine hours of capital. Any combination of labor and capital that results in total cost being $4,000 would be on the same — $4,000 — isocost curve.

I illustrate the isocost curve for this equation in Figure 6-3.

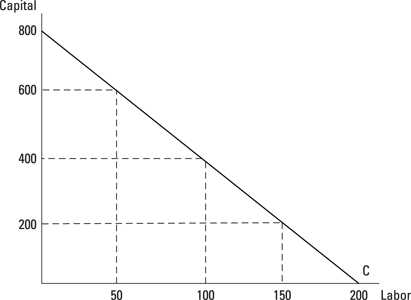
Figure 6-3: An isocost curve showing possible combinations of labor and capital you can employ for $4,000.

Changes in input prices shift the isocost curve. If the input on the horizontal axis becomes cheaper, the isocost curve rotates out on that axis as illustrated in Figure 6-4. If the input on the vertical axis becomes cheaper, the isocost curve rotates as illustrated in Figure 6-5. More expensive inputs cause shifts in the opposite direction.

Figure 6-4: Lower input price on the horizontal axis.

Figure 6-5: Lower input price on the vertical axis.

Making the most with the least: Cost minimization

In order to maximize profits, you must produce your output at the lowest possible cost.

The costs of producing a given quantity of output are minimized at the point where the production isoquant is just tangent — or, in other words, just touching — the isocost curve. This point is illustrated as point A in Figure 6-6. The cost-minimizing combination of labor and capital are the quantities L0 and K0.

Figure 6-6: Cost-minimizing input combination.

Now comes the easy part. At the point where you minimize costs, the production isoquant and isocost curve are tangent. This means the slopes of these two curves are equal. Therefore

Or, if you rearrange that equation

Thus, you minimize costs when the marginal product per dollar spent on each input is equal for all inputs. And this holds true no matter how many inputs you use!

Economists call the preceding concept the least cost criterion, and it’s an application of the equimarginal principle. To produce goods with the lowest possible production cost, you equate the marginal product per dollar spent.

Minimizing Cost with Calculus (If You Want)

Dangerous intersection ahead. Not really, because a mathematician calls this a tangency, not an intersection. In this section, I show you how to determine the cost-minimizing input combination with calculus, but remember, use calculus only if you want to. Otherwise, simply use the least cost criterion in the previous section.

Cost minimization is another constrained optimization problem. In this situation, you want to minimize the cost of producing a given quantity of output. And with any constrained optimization problem, the Lagrangian function is the perfect tool. (Go to Chapter 3 for more information on the Lagrangian function and how to set it up.)

Your business decides to produce 3,200 units of product daily by using two variable inputs — labor, L, and capital, K. (This problem can have more than two variable inputs; the algebra is simply a little more complicated. See the steps for making a Lagrangian function in Chapter 3.) The relationship between your total product, 3,200, and the inputs of labor and capital is described by the following equation

Assume the price of labor is $20 per hour and the price of capital is $5 per machine-hour. The resulting isocost curve is

Your goal is to minimize the cost of producing 3,200 units of output. The steps you take in order to determine the cost-minimizing amounts of labor and capital are as follows:

1. Create a Lagrangian function.

Recognize that the variable you’re trying to minimize is cost. So, your objective function is 20L + 5K. Second, your constraint is represented by the desired output level, 3,200. The constraint based upon your production function is 3,200 — 16L0.5K0.5. Your Lagrangian function is

2. Take the partial derivative of the Lagrangian with respect to L and K, the inputs you’re using, and set them equal to zero.

These equations ensure that cost is minimized.

3. Take the partial derivative of the Lagrangian function with respect to λ and set it equal to zero.

This partial derivative ensures that the production constraint is satisfied.

4. Solve the three partial derivatives simultaneously for the variables L, K, and λ to minimize the cost of producing 3,200 units of output.

Rewriting the partial derivative of £ with respect to L enables you to solve for λ.

Substituting the previous equation for λ in the partial derivative of £ with respect to K yields

so

Finally, substituting 4L for K in the constraint (the partial derivative of £ with respect to λ) yields

Therefore, you need to use 100 hours of labor.

Earlier you determined K = 4L.

So you should use 400 machine-hours of capital.

Finally, you can solve for λ.

Therefore, the combination 100 hours of labor and 400 machine-hours of capital minimizes the cost of producing 3,200 units of output. In addition, λ equals 1.25. Because lambda indicates the change that occurs in the objective function given a one-unit change in the constraint, it indicates that if you produce one more unit of output, your cost increases by $1.25. This is a great situation if you can receive more than an additional $1.25 in revenue from selling that extra unit.

Recognizing That More Isn’t Always Better with Long-Run Returns to Scale

In the long run, all inputs can be changed. If you change all inputs by the same percentage or proportion, you need to know the amount output will change by. Economists call this relationship between output and all inputs returns to scale.

Returns to scale refers to the changes in output that occur when the scale of production changes. Changes in the scale of production indicate a proportional change in the quantity employed of all inputs.

Increasing returns to scale indicate that doubling the quantity employed of all inputs results in the quantity of output produced more than doubling. Increasing returns to scale can be caused by greater specialization within your company, or perhaps doubling your inputs allows you to build one large factory that’s more efficient than two small factories. A number of factors lead to increasing returns to scale.

Decreasing returns to scale indicate that doubling the quantity employed of all inputs results in the quantity of output produced less than doubling. Decreasing returns to scale may result from the fact that larger business enterprises are harder to coordinate than smaller businesses. As a consequence, it’s more difficult for you to convey your intent and to directly monitor the operation of specific areas of a larger business.

Constant returns to scale indicate that doubling the quantity employed of all inputs results in output also doubling. In the case of constant returns to scale, increasing and decreasing returns to scale essentially offset each other.

Determining Output Elasticity

Output elasticity is the percentage change in output that results from a one-percent change in the quantity employed of all inputs. Output elasticity, therefore, is related to returns to scale. If the output elasticity is greater than one, increasing returns to scale exist. An output elasticity equal to one indicates constant returns to scale, while an output elasticity of less than one indicates decreasing returns to scale.

Consider the Cobb-Douglas production function

If you increase the quantity employed of both labor and capital by one percent, then

Rearranging the equation results in

Therefore, a one-percent increase in both labor and capital results in a one-percent increase in output, as represented by the (1.01) in the equation. This situation indicates constant returns to scale.

One special feature of Cobb-Douglas production functions is that they always have constant returns to scale. Just a final little piece of production magic.