WEB–APPENDIX N

CONTINUOUS INTEREST RATES

To understand the intuition of the continuous interest rate, let us reexamine the commonly used interest rate, which is more formally referred to as the simple interest rate per period. Simple interest rate is paid once over the period. For example, a bank deposit of $100 today with an annual simple interest rate of 10% will be worth:

$100 × (1 + 0.10) = $110

next year. What happens when the deposit is compounded semiannually? This means the bank will compound the value or pay the depositor interest twice, and uses each time 10%/2 = 0.05 as the interest rate. Then, the deposit will be worth $100 × (1 + 0.05) = $105 after six months, and 105 × (1 + 0.05) = $110.25 = (1 + 0.05)² at the end of the year. This is greater than $110, the amount tha the depositor would receive with annual compounding. Thus, the depositor, as a lender, will prefer compounded semiannually to compounded annually.

What happens if the deposit is compounded quarterly? The depositor will then get paid 10%/4 every quarter, and hence get:

(1 + 0.025)⁴ = 1.1038

at the end of the year. In general, if the interest payments are compounded m times a year, a loan of value V₀ today will be worth at the end of year,

where r is the stated annual interest rate. For example, if the interest payments are compounded 365 times a year (compounded daily) and the stated interest rate is 10%, a deposit of $1,000 will be worth:

$1,000(1 + 0.10/365)³⁶⁵ = $1.105

As the number of compounding m becomes larger and larger, the compounding interval becomes smaller and smaller. As m approaches infinity, it is as if we are compounding at every instant, that is, there is continuous compounding. The continuously compounded value at the end of year will be:

where e = 2.71828, the basis of natural log and a constant. Assuming a stated interest rate of 10%, the value is $1,105.1708, not much different from the value with daily compounding.

An analytical proof of equation (N.2) follows from calculus. Taking the logarithm on the right-hand side of equation (N.1), we need only to show:

If r = 0, the result is obvious. If r ≠ 0, we can rewrite this as:

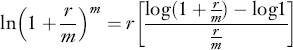
By the definition of derivatives, we know:

That is, the limit is the r times the derivative of the function log x when x = 1, and hence is equal to r.

To distinguish them, we denote by r the continuously compounded interest rate, and by R the simple interest rate. How is r related to R? At r, $1 investment will be worth e^r dollars next year. At R, it is 1 + R. The payments must be the same: e^r = 1 + R. Thus, we can compute r from R by:

r = ln(1 + R)

Alternatively, if r is known, the simple interest rate R can be obtained from r by:

R = e^r − 1

For example, if r = 10%, the equivalent simple interest rate R must be 10.5171%. On the other hand, if R = 10%, the equivalent continuously compounded interest rate must be 9.5310%.

The question is why is the continuously compounded interest rate often used in finance, especially in theory, given the above equivalence? The answer is that the above equivalence is true only if the rate is constant. In practice, interest rates change. Theoretical models often allow trading continuously and then one has to compute the interest payments every instant on the cash deposits, and accumulate them over time. To do so, one has to use continuous rates and has to use the exponential function when the rate is constant, and use integrals in addition when the rates vary over time.