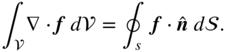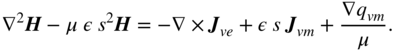Chapter 3
Maxwell's Equations
3.1 Maxwell's Equations for PEEC Solutions
One set of fundamental techniques necessary for partial element equivalent circuit (PEEC) models is the circuit techniques in Chapter 2. Furthermore, we require EM techniques that are based on Maxwell's equations presented in this chapter. We give a general overview of the different possible forms of Maxwell's equations and the resultant differential and integral equation formulations. Hopefully, this leads to the understanding of various appropriate solutions. In this chapter, we emphasize existing results and conclusions based on Maxwell's equations instead of derivations of the fundamentals on which they are based. Our aim is to provide essential tools for connecting lumped circuit analysis and electromagnetic modeling. We concentrate on solutions that have practical relevance for PEEC modeling. As an example, we can state that the type of problems we want to solve also requires a 
solution since such connections exist in these problems. Hence, it is important that our approaches include 
solutions. Hopefully, we include sufficient references for the reader who wants to study the origin of some of the concepts in more details.
3.1.1 Maxwell's Equations in the Differential Form
To start, we choose a general form of Maxwell's equation [1, 2] that includes fictitious magnetic charges 
as well as fictitious magnetic currents 
. We show that this can lead to important solution techniques while it is clear that both quantities do not exist in real-life physical systems. Importantly, these quantities result in a dual formulation in the electric field 
and the magnetic field 
, which has advantages. We need to consider time and frequency domain formulations since they both are important. For this reason, we use the Laplace transform variable 
in the frequency domain and the time derivative 
in the time domain. With this, Maxwell's equations can be written as
We use the notation 
for the electric charge volume density in 
. However, if a solution does not involve magnetic charges, we simplify the notation to 
since the electric charge is obvious. The magnetic volume charge density is 
in 
. If the electric charge is distributed only on the surface, we use the surface charge representation 
for the surface charge in 
. Of course, a magnetic surface charge density is represented by 
in 
.
Names used for the Maxwell's equation (3.1a) is the Faraday's law and (3.1b) represents Ampere's circuital law. Equation (3.1c) is the Gauss' law for electric field and (3.1d) is the Gauss' law for magnetic field. It can be shown that for the above-mentioned four equations, only two are independent. Gauss' law (3.1d) and (3.1c) can both be derived from (3.1b) and (3.1a), respectively.
The notation for current densities is analogous. The volume current density 
is the impressed electric current volume density in 
. The surface current density 
is in 
. The notation for magnetic current densities is similar. The magnetic volume current density is 
in 
. The magnetic surface current density is 
in 
. We should note that for magnetic quantities we always use the magnetic subscript index 
for clarity, such as in 
and 
. We always need to be reminded that fictional magnetic quantities can be involved.
The electric field intensity 
is in 
and 
is the magnetic field intensity in 
. Further, the displacement flux density is 
in 
. The magnetic flux density 
is in 
.
The following constitutive relations are satisfied by 
, and 
for an isotropic media:
where 
is the permeability in 
, 
is the permittivity in 
, and 
is the conductivity of the material in 
. Again, we call the conductive current 
rather than 
for the case without magnetic currents.
Other extremely important relations for our work are the so-called continuity equations. They are based on charge conservation principle and consider the time-dependent charge density variation. The relation between the electric current density and electric charge density is
Similarly, for the magnetic current density and magnetic charge density, the charge conservation law is given by
3.1.2 Maxwell's Equations in the Integral Form
For completeness we also list Maxwell's equations in an integral form. This formulation has many applications. An important one is that it forms the basis for the finite integration technique (FIT), which is a differential equation solution technique [3].
The approach is based on the integration of Maxwell's equations (3.1a) and (3.1b) over local surfaces and volumes. We present the Maxwell's equations in the time domain, which is similar to the frequency domain formulation. We use the egg-shaped half volume in Fig. 3.1 to illustrate the formulas.
Figure 3.1 Example for surface and volume for the integrals.
We start with the first two equations (3.1a) and (3.1b) to obtain
The surface integrals are over the surface 
in Fig. 3.1. The second form over the closed contour 
is obtained by applying Stokes' theorem given in the following section (3.34).
The second part of the surface formulation of Maxwell's equations is based on the Gauss' theorem in (3.33), which is
where 
is the outward normal in Fig. 3.1 to the surface 
of volume 
. To simplify the notation of the above equations, we did not indicate that the field variables in (3.5a)–(3.6b) depend on the spatial position 
and time 
.
The left-hand side of (3.5a) represents the electromotive force (emf ). Further, the left-hand side of (3.5b) is the magnetomotive force (mmf ). Both equations clearly indicate the coupling between the time-varying electric field and the time-varying magnetic field.
The electric continuity equation in the form of charge conservation is for the electric volume current given by
and for the magnetic volume current as
3.1.3 Maxwell's Equations and Kirchhoff's Circuit Laws
The fundamental idea of PEEC is to model Maxwell's equations to the circuit domain. Here, we give a general intuitive view. We pursue this issue in great detail in most chapters of this book. Chapter 1 of [1] gives a very detailed derivation and explanation for the contents of this section.
Equation (3.5a) can be interpreted as time-varying magnetic flux 
through a closed loop generating an emf, which can be represented as [1]
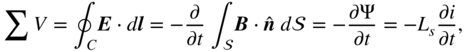
where 
is an inductance due to a loop area. The relation between magnetic flux and the current 
is given by 
. Inductance concepts are considered in detail in Chapter 5 since they are important elements in the PEEC circuit equations.
As we learned from Chapter 2, we can write the Kirchhoff's voltage law (KVL) for a resistance, inductance, capacitance (RLC) lumped circuit loop for a simple situation as
where 
may be due to a voltage source, 
is the voltage drop due to a lumped resistor, 
is the voltage drop from a lumped capacitor, and 
is the voltage drop along the lumped inductance. We also can consider that the variation of the magnetic field through a finite circuit loop area represents the KVL as
From (3.7), the connection with a capacitance can be established by the following derivation
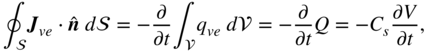
where 
is a capacitance due to the capacitive coupling between a conducting node to the ground.
As an example, a general circuit node may have parallel connected lumped R,L,C elements as well as a source current source 
in parallel. Then, the conventional Kirchhoff's current law (KCL) will yield
Hence, we can see from this example how the continuity equation can be connected to the KCL in the circuit domain. The continuity equation for PEEC is considered in Section 6.3.1.
3.1.4 Boundary Conditions
Boundaries with different properties play an important role in many relevant problems. Hence, it is important to understand how to deal with such boundary conditions in the solution of electromagnetic problems. We consider an interface between two materials as shown in Fig. 3.2, where the normal vector points from the material 2 into material 1. This leads to the following boundary conditions for different materials.
Equation (3.14a) states that the tangential components of the electric field intensity are discontinuous in the presence of a surface magnetic current. Further, (3.14b) states that the tangential components of the magnetic field intensity are discontinuous due to the interface electric current. The third equation (3.14c) states that the normal components of the displacement flux density are discontinuous due to the presence of an interface electric charge density. Equation (3.14d) states that the normal components of the magnetic flux density are discontinuous in the presence of an interface magnetic charge density.
We next consider the case where material 2 in Fig. 3.2 is a perfect electric conductor (PEC) with infinite conductivity 
. Then, the electric field 
is zero inside the conductor. For a solution where we set the nonphysical magnetic current and magnetic charge to zero, the boundary condition at the interface between material 1 and a PEC region 2 reduces to
Essentially, (3.15a) states that the tangential component of the electric field at the interface is 
. Further, (3.15d) states the normal component of the magnetic field at the interface is 
.
Figure 3.2 Example interface between two different materials.
We also want to consider the important case where material 2 is a good but nonperfect conductor. For this case, another boundary condition connecting the tangential electric field and magnetic fields is frequently used. This leads to what is called the impedance boundary condition defined as
where 
is called the surface impedance relating to the tangential components of the electrical and magnetic fields, 
and 
, respectively. This condition has an assumption that the incident filed is close to orthogonal to the surface.
3.2 Auxiliary Potentials
3.2.1 Magnetic Vector Potential 
and Electric Scalar Potential 
An important indirect approach for the solution of Maxwell's equations is based on the definition of auxiliary vector potentials. From (3.1d) we have 
. Then from the vector identity
we find that we can define 
such that it obeys the above identity. From this, it is evident that we can have
where 
is derived from the vector potential 
. Substituting (3.18) into (3.1a), we obtain for the source-free single harmonic case
Collecting the terms with the cross product, we get
We note that both terms inside the parentheses should be electric fields. Next, we use the vector identity
Comparing (3.20) and (3.21), we see that we can write
where 
is the scattered field due to all sources. 
is the electric scalar potential. If an external incident field 
is enforced, equation (3.22) can be rewritten as
Inside a lossy medium, the total field is related to the conducting current by (3.2c). Hence,
For this case, (3.23) becomes
This is also called the electric field integral equation (EFIE). We note that this is one of the foundation formulas for the PEEC method.
3.2.2 Electric Vector Potential 
and Magnetic Scalar Potential 
Analogous to the last section, the definition of an electrical vector potential 
helps the formulation of additional solution methods. This is part of the efforts in providing a dual formulation.
We start with electric displacement flux density 
that is solenoidal in a source-free region. We again use the vector identity
Hence, we can in the same way define the electric vector potential 
with 
, or
At the sourceless region, (3.1b) can be written as
Using the definition of 
, we can reduce this to
This leads to the important equation
where 
is the magnetic scalar potential.
In (3.30), 
is the scattered magnetic field due to all sources. If an external incident magnetic field 
is applied, the total field is the sum of the incident field 
and the scattered one. Hence, it is
In the absence of an external applied magnetic field, the final formulation for the magnetic field is
This is the basic magnetic field integral equation (MFIE) that is directly corresponding to the EFIE in (3.25).
3.2.3 Important Fundamental Relationships
Several important theorems can be used to facilitate the derivation and the solution of the electromagnetic wave equations. It is important to understand the mathematical formulation as well as physical meaning. Our summary of these electromagnetic theorems does not include details since many excellent textbooks exist today on the fundamentals of electromagnetics, e.g., [1].
The important Gauss' law states that the integration of the divergence of a field variable is equal to the total flux of the field variable through the surface enclosing that volume. If 
is a field vector, the mathematical representation of this theorem is
A second important law is Stokes' theorem, which states that the total curl flux of a field through a given surface is equal to the field's loop integration over the closed boundary of that surface. Its mathematical representation is
We note that we will extensively use Stokes' law in Chapter 5.
A form of Gauss' theorem considers the relationship between two scalar functions 
and 
in terms of the Laplacian operator 
. It is generally represented as
This theorem is frequently used for wave equations as well as integral equations.
3.3 Wave Equations and Their Solutions
3.3.1 Wave Equations for 
and 
The vector wave equations can be derived from Maxwell's equation for the electric field 
and the magnetic field 
. In an isotropic region, using (3.1a) and applying the curl operation on both sides results in
Using the fundamental vector Laplacian identity [4], we get
and replacing 
in (3.36) with (3.1b), we obtain
Hence, using (3.1c), the wave equations in terms of the electrical field in an isotropic region results in
Using the Duality Principle of Maxwell's equations, we can directly obtain the wave equation for the magnetic field to be
Of course, a derivation similar to (3.39) can be employed to obtain (3.40).
3.3.2 Wave Equations for 
, 
, and 
Based on the Laplacian identity (3.37), the magnetic vector potential satisfies the following expression:
Based on (3.18) and taking curl operation on both sides, we have
Because of (3.30), by combining (3.41) and (3.42), we have
We can enforce the Helmholtz equation, if the Lorenz gauge (or Lorenz condition) [1] is used, which is
for the magnetic vector potential
It is possible to express the potential 
in terms of the charge density following the same steps, which leads to the Helmholtz equation for the electric scalar potential, or
Using a similar process, we could derive the Helmholtz equation for the electric vector potential 
and also
3.3.3 Solution of the Helmholtz Equation
In the time domain, the Helmholtz equation for the magnetic vector potential 
is
For a homogeneous medium, (3.49) has a closed-form solution for the magnetic vector potential 
due to an electric current 
in the volume 
as
Equation (3.46) can be written for a homogeneous material in the time domain as
Another important closed-form solution can be obtained for an electric scalar potential 
due to the charge distribution. This formula takes into account the charge 
residing on the exterior surface of the conductors. For a homogeneous medium the solution of (3.46) is given by
In (3.50) and (3.52), 
denotes the time at which the current and charge distributions, 
and 
, act as sources for 
and 
, respectively. The source of the difference between 
and 
is the finite value of the speed of light in a homogeneous medium, which is 
. Hence, they can be related as
as considered in Section 2.11. The derivation of the relations (3.50) and (3.52) are based on Maxwell's equations as well as the Lorentz gauge (3.44).
We should note that both potentials (3.52) and (3.50) are of importance throughout this book as is evident from the following section.
3.3.4 Electric Field Integral Equation
A formula that is fundamental to the PEEC method is the integral equation derived in this section. If we write an equation for the sum of electric fields in a conductor based on (3.50) and (3.52) into (3.25) and add a possible external incident electric field 
, we obtain the important EFIE
where we consider a lossy, nonperfect conductor. The electric charge is assumed to be on the surfaces of the conductors. It is represented by the potential (3.52).
Hence, the integral equation includes (3.54) and (3.52). In addition to (3.52), we also have to enforce the conservation of charge with the continuity equation (3.7), or
Since the charge is located only on the surface of conductors, inside conductors equation (3.55) reduces to
However, for the charge on the surfaces on a conductor, we find using the surface divergence that
where 
is the outward normal to the surface 
. Finally, we can summarize the relevant equations as
The unknowns of such a problem are represented by the current density 
in the interior of the conductors, the charge density 
on the surface of the conductors, and the electric scalar potential distribution 
of conductors, which can be directly expressed as a function of the charge density for 
.
Equations (3.58a)–(3.58d) can be rewritten using the Laplace variable 
as
where 
and 
is the Laplace variable. Again, both the time and frequency domain formulations for the EFIE are fundamental to the PEEC method.
3.4 Green's Function
The Green's function is the basic solution of the wave equation for a local source, which is a point source for 3D. A solution using Green's function with respect to space variables such as 
can best be compared with the equivalent in the time domain convolution with an impulse response considered in the circuit analysis in Chapter 2. The Green's function can be compared to an impulse response in the time domain.
Two different classes of Green's functions can be defined – static and dynamic – depending on the type of wave equations for which they are a solution. Further, the homogeneous and inhomogeneous Green's functions are defined depending upon the medium environment. Specifically, inhomogeneous Green's function represents different media.
Observe that homogeneous Green's function can be used to solve inhomogeneous problems. For example, the Poggio-Miller-Chang-Harrington-Wu-Tsai (PMCHWT) integral equation method in Section 11.4.2 can be based on homogeneous Green's functions while the solution applies to nonhomogeneous problems. Also, it is important to observe that delayed static Green's functions are used in full-wave time domain PEEC models.
It is usually difficult to find closed-form solutions for inhomogeneous Green's functions for complex structures. As an example, the Green's function for the full-wave Helmholtz equation in the homogeneous medium is defined by the following wave equation for a point source:
where 
is the field point location and 
is the source point position. The wave number 
for nonzero frequencies is considered in the following section.
3.4.1 Notation Used for Wave Number and Fourier Transform
It is noted that for the regular physical wavenumber 
in the frequency domain and 
using the Laplace transform. In many books and papers, 
is also used to represent the wave number. Further, 
is also used for the phase constant, which is different from the wave number that is determined by the medium property and the frequency. The phase constant is determined by the guided wavelength. To be specific, 
, where 
is the wavelength of the electromagnetic wave in an infinite homogeneous medium for the given frequency. 
where 
is the guided wavelength of the electromagnetic wave in the specific structure at the given frequency.
Table 3.1 Notation used for propagation parameters.
| Representation | Transmission line notation | Physics notation |
| Lossless material, propagation constant |  |
 |
| Lossy material, propagation constant |  |
 |
| Lossy material, attenuation constant |  |
 |
| Lossy material, phase constant |  |
 or  |
To make the issue more complicated, for a lossy medium, 
is complex. For this case, it is usually written as 
. The real part 
corresponds to the wavelength while the imaginary part corresponds to the loss. The different usages of 
and 
can cause confusions if they are not properly distinguished. The comparison between the two notations is shown in Table 3.1. In this book, we use 
as the wave number as is done in Ref. [1] since it is a clear notation. It is also the conventional transmission line notation.
In the electromagnetic analysis, Fourier transform and its inverse are frequently used. The Fourier transform using the wave number 
from the space domain 
for 
is
Correspondingly, the inverse Fourier transform is
Other forms are also in use besides the conventional notations. The Fourier transform is used in Section 5.8.2.
3.4.2 Full Wave Free Space Green's Function
The solution of (3.60) is called the full-wave free-space Green's function
When the frequency is zero, Helmholtz equation degrades to Poisson's equation.
Its solution is called the static Green's function:
It is noted that the lowercase 
is used exclusively for scalar Green's functions. But other types of Green's functions in this book employ the uppercase 
as the Green's function symbol.
If the vector wave equation for the electric field is established based on Maxwell's equations, we have
then the corresponding Green's function is defined as the dyadic Green's function by the following equation:
where 
is the dyadic Green's function and 
the unitary dyad. As a result, the electric field solution is
where the dyadic Green's function is
In the implementation, the dyadic Green's function is expanded as a 
matrix. Its element composition is shown as follows:
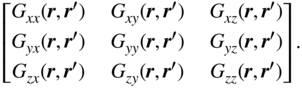
Substituting it into (3.68), we have
3.5 Equivalence Principles
Equivalence principles are very useful for solving problems with regions of different materials. They will be used for both volume- and surface-type integral equation formulations. Here, we present the so-called volume equivalence principle that we use in Chapter 10 to solve combined conductor and dielectric problems. The fundamental derivation of the method is given in the following section, while the derivation for the PEEC method is given in Section 10.4.5.
The second approach is based on the surface equivalence principle. Its basic principle is presented in Section 3.5.2 and a PEEC implementation is presented in Section 11.4.2. The formulation includes geometries with dielectric and magnetic materials where 
and 
.
3.5.1 Volume Equivalence Principle
For a region that can consist of dielectric materials with position-dependent permittivity 
and permeability 
, the field can be solved using the volume equivalence principle. In general, an external field excitation can come from a current density 
somewhere in the region of interest. Maxwell's equations for 
(3.1a) and 
(3.1b) are
If the same source is placed at the same position of a free space with 
and 
, we have
The scattered field can be computed by subtraction, or 
and 
. The results are
where 
and 
are the electric and magnetic volume current densities.
In this general form, additional equivalent volume magnetic current and equivalent volume electric current sources are used. We only consider the electrical integration formulation with the electric current density 
. This current density can be interpreted as the source of the scattered field generated in this formulation. Adding this equivalent source into the electric field equation (3.59a), the result is
If we insert the source current density into the equation, we get
We should mention that we apply this volume equivalence formulation in Chapter 10.
Figure 3.3 Illustration of surface equivalence principle for closed-surface two-region problem.
3.5.2 Huygens' Equivalence Principle
The Huygens' equivalence principle is one of the key surface equivalence principles of interest. All surface equivalence principles originate from the uniqueness theory, which states that the matching tangential field components are sufficient to guarantee a unique solution of the field. The tangential field at the surface of the region boundary must be matched inside a closed dielectric or conductor region as shown in Fig. 3.3. Potential external incident electric and magnetic fields are indicated by 
and 
, respectively. Surprisingly, the fields inside the closed boundary can be arbitrarily chosen since they do not impact the tangential fields.
A set of equivalent surface currents with any choice of the internal field 
and 
will appear based on the fundamental boundary conditions.
We observe that the flexible choice of the internal field will result in different equivalent surface currents. These equivalent currents reproduced the field outside the closed region. This is Huygens' equivalence principle.
We set the internal field 
and 
. The resultant equivalent current is named the Love's equivalent current. Importantly, the outside field is regenerated by the equivalent electric current 
and magnetic current 
. Due to (3.45) and (3.22), the contribution from 
to the 
field can be taken into account by the magnetic vector potential 
and the scalar potential 
.
Because of (3.47) and (3.30), the contribution from 
to the 
field can be counted by the magnetic vector potential 
and scalar potential 
. As a result, the 
field can be represented by the equivalent sources as follows:
Consequently, the magnetic field can be derived to be represented using the equivalent sources as follows:
Thus, 
can be obtained from (3.49). Also, 
can be obtained from the similar representations. 
shall be obtained from (3.51) using the electric charge distribution on the surface. 
shall be obtained similarly using the magnetic charge distribution on the surface.
3.6 Numerical Solution of Integral Equations
A fundamental step in the practical solution of Maxwell's equations is the discretization into finite size cells. The numerical technique used for the approximations represents an important issue. In this section, we give a general outline for integral equation techniques. PEEC is a member of this class.
All solution techniques must result in a finite but sufficiently large number of unknowns such that an accurate numerical solution can be obtained. Of course, we also want to keep the number of unknowns and the compute time as small as possible. Basically, all solution methods are based on the so-called Weighted Residuals Method (WRM), as discussed in Chapter 1 [5]. It was originally called the Method of Error Distribution Principles [6], which is also a good descriptive name since we have to make approximations in several places that introduce errors in comparison to the exact Maxwell's equations.
How the general WRM approach is employed for different formulations was illustrated in Ref. [7]. It was also illustrated how the WRM approach is applied to solve different formulations based on differential as well as on integral equations. Sometimes, the method of moments (MoM) name is also considered to be a WRM [8] technique. The problem with this is that different meanings have been associated with this name. Some researchers assume that the name is limited to integral equations, while others assume that MoM is generally same as WRM [7, 9]. Also, we should point out that MoM has no relation to the moment matching method in the macromodeling area [10, 11].
Fundamentally, the WRM solution technique consists of several steps. The first step is the discretization of objects, including conductors and dielectrics, into finite blocks, bars, or surfaces cells for which we locally preassign fixed current directions or charge distributions areas. For example, one conductor or dielectric block can be partitioned into a collection of cells. The fixed current or field distribution assigned within the cell is called the basis function. Hence, each cell has its own fixed basis function and a conductor is represented by a set of fixed basis functions for each of the cell. With this, the current direction is fixed on each cell. However, the strength of the current on each cell is unknown.
To be specific about the second approximation used, we consider the computation of capacitances where we need to match the potential on a surface as illustrated in Fig. 4.1. Similar to the basis function, the equipotential on a conductor is matched with an approximating function usually called a testing function. For example, it is quite common to match the potential at a single point only on a cell leading to the so called collocation method. However, as we see, in PEEC we want to have symmetric circuit elements. All elements such as resistors, capacitors, and inductors are fundamentally symmetrical. This requires that both the basis function and the testing functions to be the same for PEEC circuits. This condition is also called a Galerkin-type method, which has its general origin in Ref. [12].
The third key step of the WRM method pertains to the way the resultant matrix system of equations is solved [7]. In the PEEC method, this consists of solving circuit equations based on the approximated system from the first two steps. Other members of the WRM family include techniques such as least squares solutions. Further, techniques such as the Generalized Multipole Technique [13] and multipole approaches [14] should be included in the class of solutions. Since the PEEC solution is circuit oriented, its connection to WRM may not be obvious. The solution step uses a circuit solver that is more like a SPICE tool [15]. Today, numerous techniques are used to solve the resultant matrix solution faster.
We next formulate the above discussion in a symbolic operator form. In general, we can write both differential and integral equations this way.
where 
is a differential or integral equation operator. An example of a differential equation in this form is given by (3.64), and an integral equation operator example is given in (9.44). Here, 
is the unknown function of the spatial coordinate 
. We assume that the time or frequency for which the equations are solved and also 
is known. The solution with the WRM method is given next. If we subdivide the problem into N cells, we can name the fixed known basis function assigned to the jth cell to be 
. Then, if we subdivide the problem into 
cells, we can represent the solution as
We now can substitute the solution (3.82) into the operator equation (3.81) to get
where the unknowns now are the 
coefficients 
. As an example, in most PEEC models the function 
is a constant pulse function.
We can view (3.83) as a row of a matrix representing the problem. The next step with the testing function is to set up a system of equation based on an averaging integration process of the equation. Mathematically, the averaging or testing function for the 
th row of the matrix yields
while 
represents a volume, but it can also be an area 
or even a length 
. Here, 
is a weighting function that is the same as 
for the circuit and the Galerkin-type solution.
Once the basis and weighting or expansion functions are chosen, we can proceed to the third WRM step, which will solve the resultant system of equations.
Since the book is based on PEEC circuit techniques, we do not use the above mathematical formulation for the solutions. Fortunately, the circuit-oriented approach used yields a clear way to present the techniques.
Problems
- 3.1 The independence of Maxwell's equations
Derive Gauss' law for the electric field and also Gauss' law for the magnetic field from Ampere's law (3.1b) and Faraday's law (3.1a), respectively.
- 3.2 The static and dynamic fields
Assume the field is static (no time-dependent variation), rewrite Maxwell's equations and the corresponding wave equations. Point out key differences between the static field you derived and the dynamic field based on the Helmholtz equation.
- 3.3 Green's function
Let us assume the wave equation
where
is the Dirac delta function with zero value everywhere except at point 
and where its volume integral over the whole space equal to 1. Show that, for three-dimensional (3D) space, the solution of 
is
Use the conventional
as the time dependency reference. - 3.4 Magnetic field generated by currents
Assume a square conducting loop has the side length
. The conductor is assumed to have a diameter 
where (
). Assume that a uniform 
current 
is applied. Calculate the total magnetic flux created at the center of the loop. - 3.5 The electric field generated by charges
Two large zero thickness square plates with a side length
are totally overlapping. They are spaced by a small distance 
. A dielectric material is placed between the two plates with permittivity 
. We assume that the top plate is charged with a (nonphysical) uniformly distributed positive charge and an equal and opposite uniformly distributed negative charge is on the bottom plate. Assume that the nonuniform field at the plate edges can be ignored. Calculate the capacitance between the plates.
References
- 1. C. A. Balanis. Advanced Engineering Electromagnetics. John Wiley and Sons, Inc., New York, 1989.
- 2. J. A. Stratton. Electromagnetic Theory. McGraw-Hill Book Company, New York, 1941.
- 3. T. Weiland. Eine Methode zur Loesung der Maxwellschen Gleichungen fuer sechskompoentige Felder auf diskreter Basis. Archiv der Elektrischen Ubertragung, 31:116–120, 1977.
- 4. S. Ramo, J. R. Whinnery, and T. Van Duzer. Fields and Waves in Communication Electronics. John Wiley and Sons, Inc., New York, 1994.
- 5. B. A. Finlayson. The method of weighted residuals and its relation to certain variational principles for the analysis of transport processes. Chemical Engineering Science, 20:395–404, May 1965.
- 6. L. Collatz. The Numerical Treatment of Differential Equations. Springer-Verlag, Berlin and New York, 1960.
- 7. Z. D. Chen and M. M. Ney. The method of weighted residuals: a general approach to deriving time- and frequency-domain numerical methods. IEEE Antennas and Propagation Magazine, 51(1):51–70, February 2009.
- 8. R. F. Harrington. Field Computation by Moment Methods. Macmillan, New York, 1968.
- 9. J. M. Jin. The Finite Element Method in Electromagnetics. John Wiley and Sons, Inc., New York, 2nd edition, 2002.
- 10. L. Pillegi, R. Rohrer, and C. Visweswariah. Electronic Circuits and System Simulation Methods. McGraw-Hill Book Company, New York, 1995.
- 11. M. Celik, L. Pileggi, and A. Odabasioglu. IC Interconnect Analysis. Kluwer Academic Publishers, Boston, MA, Dordrecht, London, 2002.
- 12. B. G. Galerkin. Sterzhni i plastiny. ryady v nekotoykh voprosakh uprogogo ravnovesiya sterzhnei i plastin. Vestb. Inzhen. i Tekh. Petrograd, 19(2):897–908, 1915.
- 13. C. Hafner. The Generalized Multipole Technique for Computational Electromagnetics. Artech House, Boston, MA, 1990.
- 14. W. C. Chew, J.-M. Jin, E. Michielssen, and J. Song. Fast and Efficient Algorithms in Computational Electromagnetics. Artech House, Boston, MA, 2001.
- 15. L. W. Nagel. SPICE: a computer program to simulate semiconductor circuits. Electronics Research Laboratory Report, ERL M520, University of California, Berkeley, CA, May 1975.