Chapter 6
Building PEEC Models
In this chapter, we consider how partial element equivalent circuit (PEEC) models are built. Details of the discretization or meshing are given in Chapter 8. Further, the fundamental concepts on how the capacitive and inductive cell partial elements are formed have already been introduced in Chapters 4 and 5.
As shown in Section 3.6, the weighted residual method (WRM) includes important approximations. Some details are discussed in Chapter 1 and in Section 3.6.
The first one is the division or meshing of conductors or other materials into finite blocks, bars, and surface elements for which we preassign fixed local current or charge distributions. An example is a bar shown in Fig. 6.1, where we assign the current to be uniformly in the ![]() -direction. Another example is surface cells for which we assign a uniform charge density. This uniform assignment of the local current density or charge on a cell is part of what is called the basis function.
-direction. Another example is surface cells for which we assign a uniform charge density. This uniform assignment of the local current density or charge on a cell is part of what is called the basis function.
Mathematically, in general a large number of different functions are used to represent the current and voltage distributions. The choices include delta functions, piecewise constant, piecewise linear, and Rao–Wilton–Glisson (RWG) [1] set of basis and/or weighting functions. For some applications, it has been shown how triangular cells have been used for PEEC [2, 3].
The PEEC method [4] is based on the fundamental concept that basic circuit elements should be symmetrical such as conventional ones. Mathematically, this corresponds to the Galerkin WRM approach. This is accomplished by using a symmetric discrete approximation for the representation of the currents and charges for each circuit element. The basic method we use to create a finite system from the original Maxwell's equations can be viewed as WRM approximations.
We use the current density for a conductor as an example. It is shown in Fig. 6.1, where a current density is defined uniform for the conductor cross section ![]() . Hence, the current
. Hence, the current ![]() is related to the current density by
is related to the current density by ![]() , where
, where ![]() is the conductor's cross-sectional area. In the second case, for a thin or zero thickness conductor
is the conductor's cross-sectional area. In the second case, for a thin or zero thickness conductor ![]() , the surface current is defined as per unit width. It is
, the surface current is defined as per unit width. It is ![]() in the unit of amperes per unit width.
in the unit of amperes per unit width.
In general, we include some unusual cell sizes in our PEEC models, such as the use of very large aspect ratios for the cell dimensions. Further, wherever possible we use the analytical evaluation of the partial elements. As part of this, we try to adhere to rectangular or quadrilateral cell shapes.
A specific example of the weighting process is given in (6.1) for the averaging of the fields, or
where ![]() is the cross section in the thickness
is the cross section in the thickness ![]() and width
and width ![]() direction as shown in Fig. 6.1.
direction as shown in Fig. 6.1.

Figure 6.1 Example conductor bar for resistance computations.
We also give an example of the relation of PEEC to a Galerkin formulation. The weighting function averaging for the potential as is done in (6.10) and (6.11). The symmetric circuit elements are obtained with such weighting functions. In the mathematical domain, Galerkin proposed the idea of using the same basis and weighting function to solve both differential and integral equation problems [5] in 1915 using WRM. The PEEC method should be included in the class of the so-called discontinuous Galerkin methods [6], which also are popular today for noncircuit-oriented applications.
A key step in all WRM solution approaches is the way the resultant system of equations is solved. In PEEC, this consists of solving the modified nodal analysis (MNA) circuit matrix equations presented in Chapter 2. We could call this a new member of the WRM family.
6.1 Resistive Circuit Elements for Manhattan-Type Geometries
Resistances represent important circuit elements needed for PEEC models. So far, we did not consider resistances in our treatment of circuit elements since the topic is relatively straightforward in comparison to the capacitance and inductance models. We start with the classical form of Ohm's law (3.2c) as
where ![]() is the current density for any point in a conductor and
is the current density for any point in a conductor and ![]() is the conductivity of the material.
is the conductivity of the material.
The total electric field ![]() can be treated as the superposition of external fields as well as the induced scattered field, (3.54), or
can be treated as the superposition of external fields as well as the induced scattered field, (3.54), or
where the first term ![]() on the right-hand side is an externally applied electric field at
on the right-hand side is an externally applied electric field at ![]() . The scalar potential
. The scalar potential ![]() and vector potential
and vector potential ![]() contribute to the induced scattering fields.
contribute to the induced scattering fields.
For most problems, applied external source fields ![]() are zero. However, we also consider the impact of external fields for PEEC in Chapter 12. For a static case, the vector potential derivative term in (6.3) iszero. We can easily derive an equivalent circuit for the resulting equation
are zero. However, we also consider the impact of external fields for PEEC in Chapter 12. For a static case, the vector potential derivative term in (6.3) iszero. We can easily derive an equivalent circuit for the resulting equation
In Fig. 6.1, the voltage between two points “e” for end and “b” for beginning on the conducting rectangular bar is obtained by integration of (6.4). The two end-face contacts are indicated by the crosshatched areas and the dots are used as an electrical node for the contacts. The integration of (6.4) between ![]() and
and ![]() in
in ![]() yields
yields
As part of the circuit and WRM approximation, we place the contact to the entire end surfaces with the same potential. Hence, as shown in Fig. 6.1, the current density is uniformly defined to be ![]() , where
, where ![]() is the cross-sectional area. In terms of the previous discussion on WRM, we a priori assume that the current will flow uniformly in the
is the cross-sectional area. In terms of the previous discussion on WRM, we a priori assume that the current will flow uniformly in the ![]() -direction. In this unusual case, the exact current flow will be in the direction of the one assigned by the WRM model. For more complex models, current representations will be superimposed. Finally, the result for the resistance is the conventional formula
-direction. In this unusual case, the exact current flow will be in the direction of the one assigned by the WRM model. For more complex models, current representations will be superimposed. Finally, the result for the resistance is the conventional formula
where ![]() . To be consistent with the general circuit model approach, we should also average the potential evaluation in (6.5) over the contact area on the sides, or
. To be consistent with the general circuit model approach, we should also average the potential evaluation in (6.5) over the contact area on the sides, or
where ![]() is the cross-sectional area and
is the cross-sectional area and ![]() is the volume of the bar. The electric field
is the volume of the bar. The electric field ![]() is assumed uniform over the contact. The result of (6.7) is exactly the same as (6.5). With this, we can easily compute the resistance of each rectangular bar for any discretized geometry.
is assumed uniform over the contact. The result of (6.7) is exactly the same as (6.5). With this, we can easily compute the resistance of each rectangular bar for any discretized geometry.
The meshing or discretization for general complicated geometries is another challenging problem that is considered in Chapter 8. For more complex geometries, we have to further subdivide or mesh the conductive bars into rectangular subbars or cells. Then, we need to evaluate the resistance of each subbar in the geometry. The coupling between different bars is, in general, very limited. In fact, rectangular bar partial resistances are not coupled at all. However, we see that limited partial resistance coupling can occur for neighboring nonorthogonal elements as is evident from Section 7.2.2. Fortunately, for rectangular cells we only have to compute self-resistance terms. The resultant PEEC equivalent circuit is easy to solve using the circuit analysis technique presented in Chapter 2.
6.2 Inductance–Resistance (Lp,R)PEEC Models
As a next step, we consider an inductance–resistance (Lp,R)PEEC model, which is a combination of the resistance model in the last section with the partial inductances in Chapter 5. Besides the fact that these models are already useful by themselves for many applications, they also help to represent a key step toward the general PEEC model in Section 6.3.
We start with the general integral equation (3.54), or

Taking (6.2) into account but not including the capacitive potential coefficient term, we obtain

where the vector ![]() is placed inside or on the surface of the conductor.
is placed inside or on the surface of the conductor.
For simplicity, we again start out with the single bar of Fig. 6.1 as the first geometry. As before, we integrate the electric field along the length of the current path, which is between the contacts ![]() and
and ![]() , or
, or

We also note that we can simplify the dot product ![]() to
to ![]() because both vectors are in the same direction as is evident from Fig. 6.1. Again, we assume that the potential on the contacts is constant. It is equivalent to take the average of the potential over the surface of contacts, which is also very important for the second term
because both vectors are in the same direction as is evident from Fig. 6.1. Again, we assume that the potential on the contacts is constant. It is equivalent to take the average of the potential over the surface of contacts, which is also very important for the second term
where ![]() is the surface of the contact. Finally, the uniform current density is represented as
is the surface of the contact. Finally, the uniform current density is represented as ![]() . Hence, the voltage
. Hence, the voltage ![]() can be approximated as
can be approximated as
Using what we learned about partial inductances in Chapter 5, the second part is simply contribution of the partial inductance of the bar. Hence, the circuit equations for (6.11) is rewritten as
where ![]() is the partial resistance due to the loss of the conductor bar.
is the partial resistance due to the loss of the conductor bar. ![]() is the partial self-inductance. Their detailed definitions are
is the partial self-inductance. Their detailed definitions are


This represents the (Lp,R)PEEC circuit model for the single bar in Fig. 6.1, which is simply ![]() in series with the resistor
in series with the resistor ![]() .
.
6.2.1 Inductance–Resistance (Lp,R)PEEC Model for Bar Conductor
Since the PEEC equivalent circuit does not form a closed loop, the inductance of the model will be an open-loop inductance according to Section 5.4. We refer the reader to Section 5.6 for an example that consists of three partial inductances. Most likely, this model is a part of a larger structure.
It is important to use this term so that we are aware of the fact that the circuit is not closed, as is also the case for a partial inductance. Fortunately, PEEC elements have electrical nodes to connect parts together such as building blocks. Some of the parts of a PEEC circuit without capacitive elements consist of partial or open-loop inductances.

Figure 6.2 Subdivision of thin conducting panel into cells and PEEC circuit.
The example in Fig. 6.2 is a building block that consists of a simple thin metal sheet with a finite resistivity, for example, copper. We see from Fig. 6.2 how the metal panel is subdivided into cells. For this example, we divide the current into ![]() and
and ![]() components while we assume that the thickness is small enough that we do not have to subdivide it. We need to recognize that the subdivision of the current into rectangular Manhattan components is part of the WRM approximation approach.
components while we assume that the thickness is small enough that we do not have to subdivide it. We need to recognize that the subdivision of the current into rectangular Manhattan components is part of the WRM approximation approach.
Hence, this reduces the unknown currents to complex ![]() or, in the time domain response of the currents
or, in the time domain response of the currents ![]() in the cells. As usual, the cells carved out of the metal panel are electrically isolated from each other with infinitesimal gaps while the connections are at the nodes only. For clarity, we show in Fig. 6.2 only a few cells where the current vectors are shown. We should mention that the connections at the nodes have to obey the continuity equation that is given by Kirchhoff's current law (KCL) in Section 6.3.1.
in the cells. As usual, the cells carved out of the metal panel are electrically isolated from each other with infinitesimal gaps while the connections are at the nodes only. For clarity, we show in Fig. 6.2 only a few cells where the current vectors are shown. We should mention that the connections at the nodes have to obey the continuity equation that is given by Kirchhoff's current law (KCL) in Section 6.3.1.
We observe that only the cells in the same direction are inductively coupled since the dot product in (6.5) is zero for perpendicular conductors. Hence, the coupling for each element is between the parallel partial inductances only, which is similar to (6.12), or for example
There are nine partial inductances in the ![]() -direction and eight coupled inductances in the
-direction and eight coupled inductances in the ![]() -direction and nine coupled partial inductances in the
-direction and nine coupled partial inductances in the ![]() -direction. We note that the longitudinal cells along all sides are half-width cells.
-direction. We note that the longitudinal cells along all sides are half-width cells.
We see that using a half cell at the edge does in general improve the solution accuracy. Also, assume that we want to connect two of the models in Fig. 6.2 to each other. Then, we simply connect the neighboring nodes together. We also observe the neighboring edge half cells merge into full cells. We consider this as the building block approach where large problems can be viewed as being built from smaller subsystems.
The second part of the process is related to the circuit equations. We note that the circuit corresponding to applying the coupling equation (6.15) to each physical cell is in Fig. 6.2a. The resultant complete (Lp,R)PEEC equivalent circuit in Fig. 6.2b needs to be solved.
Before we consider the general case, we want to observe that the (Lp,R)PEEC equivalent circuit in Fig. 6.2b does not include a ground connection. We can declare any one of the 12 nodes as the ground. Then, the circuit analysis techniques in Chapter 2 can be used to find all voltages and currents in the solved system if a current is injected at any node. However, this may not be an issue in a PEEC model that also includes capacitances with a ground node corresponding to ![]() . However, care must be taken on a case-by-casesituation.
. However, care must be taken on a case-by-casesituation.
6.3 General (Lp,Pp,R)PEEC Model Development
This part of the chapter is dedicated to the more general class of PEEC models where we also include the capacitive currents in addition to the previous ones.
We subdivide these models into two different submodels. For example, in some integrated circuits (ICs), miniaturization leads to very high resistive circuits. Due to the high impedances, the currents are very small such that the inductive voltage drop ![]() is small. This case is considered first in the section on (Pp,R)PEEC equivalent circuits. Note that they also include capacitive terms from Chapter 4.
is small. This case is considered first in the section on (Pp,R)PEEC equivalent circuits. Note that they also include capacitive terms from Chapter 4.
For the case where the inductances are also important, the (Lp,Pp,R)PEEC circuits are considered. This is further divided into two cases according to the working frequency: (Lp,Pp,R)PEEC and (Lp,Pp,R,![]() )PEEC. Quasistatic (QS) PEEC models (Lp,Pp,R)PEEC have an upper frequency limit while the FW (Lp,Pp,R,
)PEEC. Quasistatic (QS) PEEC models (Lp,Pp,R)PEEC have an upper frequency limit while the FW (Lp,Pp,R,![]() )PEEC models can be extended, in principle, to any high frequency limit. First, we start with concepts that are necessary for the construction of these models.
)PEEC models can be extended, in principle, to any high frequency limit. First, we start with concepts that are necessary for the construction of these models.
6.3.1 Continuity Equation and KCL
The solution of a PEEC circuit also needs to satisfy the continuity equation (3.3) for the charge conservation as shown in Chapter 3.

Figure 6.3 Example cell division with both inductive filaments and capacitive cells.
In the time domain, it seems to be a simple approach to use the continuity equation (6.16) to replace the capacitive charge in the solution with currents in the overall solution as
This result is what we call a current-only electric field integral Equation (cEFIE) formulation that is widely used for a dynamic electromagnetic solution.
However, this approach leads to an overall ![]() behavior that is singular for very low frequencies
behavior that is singular for very low frequencies ![]() . This is a problem for electronics type problems. For example, a remotely located antenna does not couple at
. This is a problem for electronics type problems. For example, a remotely located antenna does not couple at ![]() . Then, such a solution is appropriate. From a circuit's point of view, this is similar to a high pass filter where the low frequencies are irrelevant. Hence, this approach is mostly suitable for problems that do not require a
. Then, such a solution is appropriate. From a circuit's point of view, this is similar to a high pass filter where the low frequencies are irrelevant. Hence, this approach is mostly suitable for problems that do not require a ![]() solution.
solution.
In the PEEC approach, since the capacitance and inductances are separate, a ![]() to daylight full-spectrum solution is possible by using the continuity equation (6.16). The continuity equation needs to be satisfied at each PEEC node as shown in Fig. 6.3. We can see four inductive cells joining a capacitance surface area.
to daylight full-spectrum solution is possible by using the continuity equation (6.16). The continuity equation needs to be satisfied at each PEEC node as shown in Fig. 6.3. We can see four inductive cells joining a capacitance surface area.
First, we apply a Gaussian surface over the area that corresponds to the node at the center of the volume covered with the capacitive cell ![]() on both top and bottom. It is clear that, if we apply Gauss surfaces to each cell in Fig. 6.3, we will wrap up the entire volume of the center part of the conductors. Multiple applications of the continuity equation will cover the entire area.
on both top and bottom. It is clear that, if we apply Gauss surfaces to each cell in Fig. 6.3, we will wrap up the entire volume of the center part of the conductors. Multiple applications of the continuity equation will cover the entire area.
Surface charge is present on both surfaces ![]() of the conductive cells of the finite thickness conducting cells shown in Fig. 6.3. The top and bottom surfaces
of the conductive cells of the finite thickness conducting cells shown in Fig. 6.3. The top and bottom surfaces ![]() have capacitive charge. In the following section, it is shown that the charge is on the surface only.
have capacitive charge. In the following section, it is shown that the charge is on the surface only.
The Gaussian volume ![]() over which we integrate the continuity equation also includes the side surface where the current flows. This results in
over which we integrate the continuity equation also includes the side surface where the current flows. This results in

where one of the Gaussian volumes ![]() and the surface
and the surface ![]() includes all sides as indicated in Fig. 6.3, where the charge is on top and bottom and thecurrent flows through the internal surfaces
includes all sides as indicated in Fig. 6.3, where the charge is on top and bottom and thecurrent flows through the internal surfaces ![]() .
.
By comparing this result with Fig. 6.3, we see that the normal direction current flow occurs through the four partial inductance cross sections ![]() of the conductors. Since they are interior to the structure, the charge density
of the conductors. Since they are interior to the structure, the charge density ![]() is zero. We notice that the integrals over the side cross sections are
is zero. We notice that the integrals over the side cross sections are

where ![]() is the total current flowing into the four partial inductance cells.
is the total current flowing into the four partial inductance cells.
On the other hand, the conductor top and bottom surfaces are charged with surface charge densities ![]() . Integrating over both top and bottom surface will yield
. Integrating over both top and bottom surface will yield

Finally, we add up all the contributions for all surfaces to yield

It is clear that this is exactly the KCL equation at the node. Hence, we recognize that applying the KCL at each node is the same as applying the continuity equation. Simply stated, the solution of the circuit equations by the techniques of Chapter 2 with the above meshing will satisfy the continuity equation.
6.3.2 Relaxation Time for Charge to Surface
An important issue to validate is if the charge is indeed on the conductor surfaces even for the highest frequencies involved. The time domain equivalent is that the charges must appear on the surfaces faster than the fastest transients in the time domain responses. We start with the Maxwell's equation (3.1c) and the displacement flux density definition ![]() .
.
where the last step is valid for piecewise continuous dielectrics. On the other hand, we can insert the conducting current ![]() into the continuity equation (6.16) to obtain
into the continuity equation (6.16) to obtain
Replacing ![]() with (6.21) yields the differential equation
with (6.21) yields the differential equation
The solution of this simple differential equation is given by
Hence, the time constant is ![]() . As an example, we consider the copper conductor for microelectronics. Its conductivity
. As an example, we consider the copper conductor for microelectronics. Its conductivity ![]() and the permittivity
and the permittivity ![]() . Thereby, the corresponding time constant
. Thereby, the corresponding time constant ![]() . It means that the charge density inside a conductor will disappear in the volume much faster than any transient signal. Hence, we can safely assume the charge density is zero inside conductors. The charges only reside on surfaces. Then in the interior of conductors the continuity equation (3.55) becomes
. It means that the charge density inside a conductor will disappear in the volume much faster than any transient signal. Hence, we can safely assume the charge density is zero inside conductors. The charges only reside on surfaces. Then in the interior of conductors the continuity equation (3.55) becomes
while on the surfaces of conductors, using the surface divergence, we have
where ![]() is the outward normal to the surface
is the outward normal to the surface ![]() .
.
6.3.3 Physical Aspect of the Capacitance Model
We considered most aspects of the building or PEEC models with the exception of the capacitive part. Also, stand-alone capacitance computations have been treated in Chapter 4. Here, we consider the capacitance term for PEEC models.
We again start with the total electric field ![]() equation (3.58d)
equation (3.58d)
where the capacitance part is represented by the gradient ![]() . The electric field generated by the scalar potential
. The electric field generated by the scalar potential
The scalar potential ![]() is related to the charge distribution by equation (3.46) as
is related to the charge distribution by equation (3.46) as

We can consider each direction separately by denoting ![]() since they will turn into different capacitive elements. Hence, the terms to be added are of the form
since they will turn into different capacitive elements. Hence, the terms to be added are of the form
We use the same symmetrical WRM discretization as we apply for the other circuit elements. As in Chapter 4, we are averaging potentials over the capacitive cells. Hence, we have to apply the symmetric integration to obtain voltages ![]() , which is defined as
, which is defined as

If we apply this to (6.30), we get
where ![]() is a volume. The charge is confined to the surface of the conductors such that we can eliminate the conductor cross-section
is a volume. The charge is confined to the surface of the conductors such that we can eliminate the conductor cross-section ![]() in the derivation. Next, we approximate the derivative using the central finite difference scheme
in the derivation. Next, we approximate the derivative using the central finite difference scheme
It means that the centers of potential cells are half a step shifted with respect to the center of the inductance cell. To clearly illustrate this, Fig. 6.4 taken from Chapter 8, Fig. 8.2 is shown here.

Figure 6.4 Inductive and capacitive cells for thin metal panel.
We see that the potential or capacitive cells are centered at the nodes, whereas the inductive cells are connected between the nodes. We also observe that some capacitive cells are corner quarter cells or side half cells in addition to the full cells.
To consistently apply the averaging in the derivation, we also average the evaluation point over the cell

where ![]() represents the positive half shift in position. Bringing (6.33) into (6.32), and applying the averaging process to (6.32), results in
represents the positive half shift in position. Bringing (6.33) into (6.32), and applying the averaging process to (6.32), results in

where the charge density ![]() over the cell is replaced by the total charge
over the cell is replaced by the total charge ![]() on that cell.
on that cell. ![]() is the free space Green's function from Section 3.4.2
is the free space Green's function from Section 3.4.2
where the time delay due to the finite value of the speed of light in the vacuum has been neglected, for example, ![]() for the QS case. From this derivation, we can also define the partial potential coefficient as
for the QS case. From this derivation, we can also define the partial potential coefficient as

Potential coefficients are similar to partial inductances in terms of the fact that each cell couples to all other capacitive surface cells in the system. Hence, it corresponds to a dense coupling network and thereby a dense linear algebra matrix in the numerical model. The following section considers how the capacitance models derived in this section can be implemented into the PEEC circuits.
6.3.4 Equivalent Circuits for PEEC Capacitances
Models that include only capacitance and their computations are introduced in detail in Section 4.5.2. Here, we concentrate on the aspect that pertains to the complete PEEC model construction. Equations (4.39a)–(4.39c) are used for the capacitive circuit model. Figure 4.16 is repeated for the three-cell system for convenience in Fig. 6.5. The partial coefficient of potential equations for this example are
Chapter 4 considers how to obtain a capacitance equivalent circuit as shown in Fig. 6.6.

Figure 6.5 Three zero thickness capacitance cells example.

Figure 6.6 Example PEEC capacitance model for small three-cell example.
A more efficient model is desirable for general PEEC models, while this model is appropriate for some small problems. As was considered in Section 2.7.3, we want to connect the capacitance model at the nodes with the total current ![]() . We start with (6.38), or
. We start with (6.38), or ![]() . To obtain an efficient formulation, we subdivide
. To obtain an efficient formulation, we subdivide ![]() into a diagonal part
into a diagonal part

and a part with the off-diagonal elements

Hence, all we did so far is to split the ![]() matrix into two parts
matrix into two parts
where ![]() is easily invertible since it is a diagonal matrix
is easily invertible since it is a diagonal matrix

If we left-multiply (6.41) by ![]() , we get
, we get
where ![]() is the identity matrix. With the definition of
is the identity matrix. With the definition of ![]() as
as
we can simplify (6.43) by differentiating both sides with respect to time to the important form
Since ![]() , equation (6.45) leads to
, equation (6.45) leads to
where ![]() includes the current of all the elements connected to the capacitor nodes. We note that this equation corresponds to the equivalent circuit in Fig. 6.7 where the current controlled current sources (CCCS) are given by
includes the current of all the elements connected to the capacitor nodes. We note that this equation corresponds to the equivalent circuit in Fig. 6.7 where the current controlled current sources (CCCS) are given by


where the coefficients are represented in the ![]() matrix (6.44). We should note that we can include the delay or retardation between the capacitive cells by including them in the current source models.
matrix (6.44). We should note that we can include the delay or retardation between the capacitive cells by including them in the current source models.

Figure 6.7 Current source capacitance equivalent circuit model for retarded PEEC model.
6.3.5 (Pp,R)PEEC Resistive Capacitive Inductor-Less Models
A (Pp,R)PEEC model without partial inductances is the only combination of partial elements we did not treat so far. Examples using these models are relevant for very high resistive circuits. Because the inductive voltage drops are relatively small compared to voltage drops over high resistive components, the inductive voltage drops are of minor importance to the overall calculation accuracy. Then, partial inductances ![]() could be ignored in the PEEC model. Due to the continuous miniaturization of integrated chips, the internal resistive loss is increasing when the cross section of copper wires is decreasing. Hence, inductances could be ignored at low frequencies for some interconnect parasitic modeling. To construct a (Pp,R)PEEC model, the process is straightforward since all partial self- and mutual inductances can be ignored.
could be ignored in the PEEC model. Due to the continuous miniaturization of integrated chips, the internal resistive loss is increasing when the cross section of copper wires is decreasing. Hence, inductances could be ignored at low frequencies for some interconnect parasitic modeling. To construct a (Pp,R)PEEC model, the process is straightforward since all partial self- and mutual inductances can be ignored.
It is clear that we have two choices to include resistances in the MNA equations. Due to the absence of the partial inductance part, the circuit matrix can be restructured, depending on which resistor stamp is used. Conventionally, we use the Table B.3 combined with the partial inductance as outlined in Table B.7 in Appendix B to reduce the number of unknowns. For the models without ![]() , we can also use Table B.2 stamp to further reduce unknowns.
, we can also use Table B.2 stamp to further reduce unknowns.
6.3.6 Delayed (Lp,Pp,R, )PEEC Models
)PEEC Models
So far, Quasi Static QS models are considered in most of our derivation. Fundamentally, the QS models are only valid when the overall dimensions of the system such as the length of the signal transmission lines is small compared to the wavelength in the spectrum corresponding to the highest frequency applied by the sources. If the highest frequency corresponds to the wavelength ![]() that is comparable to or smaller than the overall object's size, full-wave (FW) models become necessary. FW means that the frequency dependency is completely considered in the modeling process for all propagation modes. The finite speed of wave propagating is considered.
that is comparable to or smaller than the overall object's size, full-wave (FW) models become necessary. FW means that the frequency dependency is completely considered in the modeling process for all propagation modes. The finite speed of wave propagating is considered.
Conventionally, the largest physical size of all PEEC model cells ![]() for the subdivided system requires that for all cells
for the subdivided system requires that for all cells ![]() , where
, where ![]() is the working wavelength of the highest frequency component. In the time domain, the delay or retardation time is
is the working wavelength of the highest frequency component. In the time domain, the delay or retardation time is ![]() between any two elements, which are
between any two elements, which are ![]() where
where ![]() is the speed of light in vacuum. In the frequency domain or phasor format, the corresponding concept is the phase delay
is the speed of light in vacuum. In the frequency domain or phasor format, the corresponding concept is the phase delay ![]() . Here, the vectors
. Here, the vectors ![]() and
and ![]() are the points for which the delay factor is calculated.
are the points for which the delay factor is calculated.
It is important to add additional insights to this statement. Conventional TEM-mode transmission line models are physically long with a constant two-dimensional cross section. For this case, QS capacitances and inductances are appropriate 2D transmission line parameters. However, if the cross-sectional dimensions become comparable to the highest frequency wavelength, then retardation becomes relevant for the cross-section.
6.3.7 Simple Full-Wave (Lp,Pp,R, )PEEC Models Implementation
)PEEC Models Implementation
Using zero-volt voltage sources is a common approach to compute current unknowns in an MNA SPICE-type circuit. We use the approach from Ref. [7] to set up the PEEC equations in a conventional SPICE solver using the SPICE input language current using NMA stamps in Appendix B. We also use this approach for analytical studies for small circuits. However, for the implementation of large circuit solvers, we use the approach presented in the following section and in Section 2.7.3.

Figure 6.8 Small (Lp,Pp,R, ) PEEC equivalent circuit model with current sources.
) PEEC equivalent circuit model with current sources.
In Fig. 6.8, we show an elementary equivalent PEEC circuit for a single PEEC loop using the voltage sources. Today, we use the efficient formulation in (6.54) for an efficient solver implementation. However, for some experiments and analytical formulations, we can use the approach based on Ref. [7] where the circuit equations are formulated without using the matrix KCL given in Section 2.7.1. From the previous section, we can determine the coupling capacitive current sources in the frequency domain as

The total capacitive currents ![]() and
and ![]() are coupled using zero-volt and zero-resistance voltage source stamps. This is a common way to measure the current using MNA stamps in Appendix B. Hence, the delay term
are coupled using zero-volt and zero-resistance voltage source stamps. This is a common way to measure the current using MNA stamps in Appendix B. Hence, the delay term ![]() is included in the above potential coupling formulation. The rest of the circuit matrix is done using conventional MNA stamps in Appendix B.
is included in the above potential coupling formulation. The rest of the circuit matrix is done using conventional MNA stamps in Appendix B.
Next, we give an example for setting up the MNA equation by using conventional KCL and Kirchhoff's voltage law (KVL) equations in the frequency domain. For a FW formulation, the model has to include models for the retardation. Starting with the KCL for nodes 1 and 2, we have
The KCL at the capacitor 1 is given by

and for capacitor 2

It is seen that the zero-volt voltage source enables the separation of KCL equations by adding ![]() and
and ![]() to the unknowns. Note that
to the unknowns. Note that ![]() is the delay between the two capacitive cells. We also have the following two KVL equations due to the added voltage sources
is the delay between the two capacitive cells. We also have the following two KVL equations due to the added voltage sources
Finally, we can set up the MNA matrix from the above equations as
This leads to the solution of the circuit equations in the frequency domain for one basic PEEC loop. We again note that this type of PEEC model can be implemented using the conventional SPICE input language for (QS)PEEC models.
6.4 Complete PEEC Model with Input and Output Connections
In this chapter, we so far considered all aspects of PEEC models with the exception of the terminals with which the PEEC model connects to the inputs and outputs or other circuits.
We want to consider the transfer function for a full PEEC circuit. At this point, we assume that the geometry is defined and meshed and all the partial elements are computed. For most realistic problems, a small number of input sources are defined. Importantly, all the elements of the unknown vector, the potentials and inductive current can be defined as outputs. This is very convenient since this adds flexibility and we can compute quantities such as impedances.

Figure 6.9 Quasistatic PEEC model for three fundamental loops.
6.4.1 Full-Wave Models
The FW circuit model has also been described in Chapter 2. We have a so-called PEEC descriptor type model of the circuits in the form of (6.54) where we also add voltage sources ![]()
The key difference is that ![]() is a diagonal matrix such that the inverse does not add additional costs to the solution.
is a diagonal matrix such that the inverse does not add additional costs to the solution. ![]() represents the off-diagonal part of the partial coefficient of potential (6.44) matrix that does not have to be inverted.
represents the off-diagonal part of the partial coefficient of potential (6.44) matrix that does not have to be inverted.
6.4.2 Quasistatic PEEC Models
First, we take the simple case of a QS model with a capacitance model and, of course without the current source model introduced in Chapter 2. In this section, we again call the input current ![]() , which is our usual notation. Figure 6.9 shows a conventional (QS)PEEC model where the capacitances can be represented by a two-terminal capacitance matrix as is done in (4.7). It is evident from this that a QS model consists of entirely conventional circuit elements, including partial mutual inductances as shown in Fig. 6.9. This capacitance model is equivalent to the full wave (FW) capacitance model (6.54) if the delays are set to zero.
, which is our usual notation. Figure 6.9 shows a conventional (QS)PEEC model where the capacitances can be represented by a two-terminal capacitance matrix as is done in (4.7). It is evident from this that a QS model consists of entirely conventional circuit elements, including partial mutual inductances as shown in Fig. 6.9. This capacitance model is equivalent to the full wave (FW) capacitance model (6.54) if the delays are set to zero.
where we can define the input source part as

where ![]() is the vector of inputs. Since this formulation requires the inverse
is the vector of inputs. Since this formulation requires the inverse ![]() , it is computationally not very efficient. Also, the model uses passive circuit elements and only inductive couplings, while the capacitances are shown to be equivalent to capacitance model in Fig. 6.9.
, it is computationally not very efficient. Also, the model uses passive circuit elements and only inductive couplings, while the capacitances are shown to be equivalent to capacitance model in Fig. 6.9.

Figure 6.10 Example of sources associated with a PEEC model node.
We want to clearly specify the variables involved in the transfer function for the model. It is sufficient to consider a single node from Fig. 6.9 for this purpose. An input current source ![]() and an input voltage source
and an input voltage source ![]() is shown in Fig. 6.10. The existence of the sources at each node is specified by the selector matrix
is shown in Fig. 6.10. The existence of the sources at each node is specified by the selector matrix ![]() .
.
An output vector for node 1 consists of the potential ![]() and/or the inductive branch current
and/or the inductive branch current ![]() as part of the
as part of the ![]() . The presence or the absence of sources in the circuit is represented by the matrices
. The presence or the absence of sources in the circuit is represented by the matrices ![]() and
and ![]() . It should be evident that the input and output selector matrices are the same also for (FW)PEEC models with delays.
. It should be evident that the input and output selector matrices are the same also for (FW)PEEC models with delays.
6.4.3 Input and Output Selectors
In a matrix form, we need to select the appropriate inputs and outputs for the problem at hand. For this, we chose the conventional form of the MNA equations that works for both the above QS and the FW equations
where ![]() can consist of output currents, voltages, or both and
can consist of output currents, voltages, or both and ![]() is a vector of inputs as defined above. The matrix
is a vector of inputs as defined above. The matrix ![]() is the output selector matrix.
is the output selector matrix.
The definition of the different matrices for the delay case is clear by comparing (6.54) with (6.57) where


and the right-hand side is

The solution vector in the frequency domain is

that completes the description in the frequency domain.
The translation into the time domain is also rather straightforward by replacing the Laplace variable ![]() with
with ![]() . Since the matrices including
. Since the matrices including ![]() and
and ![]() are independent of time or
are independent of time or ![]() , the only difference is the system itself which is in time
, the only difference is the system itself which is in time
Note the similarity between the frequency and the time domain formulations.
As the last step in this section, we want to point out that the transfer function can be of an impedance, admittance, or a mixed type since both the inputs and outputs can be of different types. For this reason, we use the transfer function ![]() notation
notation
where finally the general transfer function is
Hence, the above equations represent the general system to be solved.
6.4.4 Power/Energy Type Circuit Model
For completeness, we derive a power/energy formulation for Quasi-static PEEC models. This is based on similar derivations in Ref. [8] and other circuit-theory texts. By denoting with ![]() the complex current vector, the general matrix KCL (2.37) can be written as
the complex current vector, the general matrix KCL (2.37) can be written as
for the equivalent circuit shown in Fig. 6.9. Here, ![]() is the current for the connected capacitances,
is the current for the connected capacitances, ![]() represents the Current Controlled Current Source (CCCS) current,
represents the Current Controlled Current Source (CCCS) current, ![]() denotes the currents flowing in the inductances while
denotes the currents flowing in the inductances while ![]() are the currents of the external current sources. Note that this is not related to the potential external current
are the currents of the external current sources. Note that this is not related to the potential external current ![]() defined in this section.
defined in this section.
The corresponding voltages for all four contributions, according to Section 2.7.2, are given by
We use the short circuit capacitances ![]() instead of the two terminal capacitances shown in Fig. 6.9. Then, the (QS)PEEC–MNA given by (2.11) is somewhat simpler since we do not have to use the delayed capacitance model for the QS case. This leads to (6.55), or
instead of the two terminal capacitances shown in Fig. 6.9. Then, the (QS)PEEC–MNA given by (2.11) is somewhat simpler since we do not have to use the delayed capacitance model for the QS case. This leads to (6.55), or

Next, we form the energy type products, ![]() where
where ![]() is the conjugate complex of the current vector
is the conjugate complex of the current vector ![]() . Premultiplying (6.65) with
. Premultiplying (6.65) with ![]() yields
yields
However, we noticed before in (2.38) that ![]() , which we use again for the identity matrix and
, which we use again for the identity matrix and ![]() ,
, ![]() and
and ![]() . Using this fact and by comparing this result with (6.66), we can simplify the result to
. Using this fact and by comparing this result with (6.66), we can simplify the result to
where the last term includes external currents.
Considering any single port to observe the behavior of the system since final result (6.68) includes the entire system. Hence, the right-hand side can be reduced to ![]() . It is a standard approach to compute the input impedance
. It is a standard approach to compute the input impedance ![]() as
as

If the direction of the current is taken into account, the input impedance can be written as
As a first observation, it is clear that this function has to be positive on the positive imaginary axis ![]() . The first term on the right-hand side relates to the capacitance model, whereas the last term represents the resistance and partial inductance model. The advantage of this formulation is that we can separately check the inductance/resistor and the coefficient of potential or capacitance models. It is clear that the two models have to be positive independent of each other for all frequencies.
. The first term on the right-hand side relates to the capacitance model, whereas the last term represents the resistance and partial inductance model. The advantage of this formulation is that we can separately check the inductance/resistor and the coefficient of potential or capacitance models. It is clear that the two models have to be positive independent of each other for all frequencies.
6.4.5 Resistances, Inductance, and Capacitive Terms
So far, we did not consider the resistors in series with the inductors. We start with the inductance part of the circuit description of the
where the last step on the right-hand side is due to the matrix voltage law (6.66c). Taking the transpose of the last two parts of (6.72) and substituting it into the Lp,R part of (6.71), we get
Two observations further simplify this result. First, we can subdivide the equation into an inductive and a resistive part. Second, both the ![]() and the
and the ![]() matrices are symmetrical. This leads to
matrices are symmetrical. This leads to
It is well known that a properly computed partial inductance matrix ![]() is symmetrical and positive definite. Also, we use the definition of positive definiteness [9].
is symmetrical and positive definite. Also, we use the definition of positive definiteness [9].
It now is clear that in (6.74) ![]() in the right half of the
in the right half of the ![]() -plane
-plane ![]() where
where ![]() . Again, we only consider a (QS)PEEC model.
. Again, we only consider a (QS)PEEC model.
The capacitive term can again be treated separately from the input impedance matrix (6.73) as
where the last part has been added for the (QS)PEEC model. We have a simpler capacitance model with one current for the connection to the nodes, which we call ![]() . For the QS case considered, we take the first equation of (6.55) as
. For the QS case considered, we take the first equation of (6.55) as
We can simplify this by using the matrix KCL (Section 2.7.1) to
since the capacitance model is connected directly to the nodes where ![]() is not included since it is a unity matrix. Inserting this for
is not included since it is a unity matrix. Inserting this for ![]() in (6.75), we get for the QS case that
in (6.75), we get for the QS case that

It is clear from the positive definite Definition 6.1 that this part is also positive in the right half plane where ![]() . We also know that the capacitive model can be replaced by a set of conventional coupled capacitances as is shown in Fig. 6.9. If the capacitances are computed accurately, we know that the capacitive part is passive. More details on these issues are considered in Section 4.4.1.
. We also know that the capacitive model can be replaced by a set of conventional coupled capacitances as is shown in Fig. 6.9. If the capacitances are computed accurately, we know that the capacitive part is passive. More details on these issues are considered in Section 4.4.1.
Hence, we can conclude the following:
Based on the above derivation (see also Refs [10] and [11]), it is shown that the transfer function ![]() is passive. More details on passivity issues are given in Chapter 13.
is passive. More details on passivity issues are given in Chapter 13.
6.5 Time Domain Representation
According to (6.64), the PEEC EM model can be described by the transfer function ![]() where the responses are given by
where the responses are given by
This can be transformed to the time domain to
where ![]() represents the convolution operator. Hence, the cascading of solutions is more time consuming in the time domain. However, techniques such as the recursive convolution approach presented in Section 2.10.2 speed up the process.
represents the convolution operator. Hence, the cascading of solutions is more time consuming in the time domain. However, techniques such as the recursive convolution approach presented in Section 2.10.2 speed up the process.
Problems
- 6.1 PEEC circuit model for coupled current strips
A rectangular strip has a width of
 and a length of
and a length of  . Its thickness is zero. Set
. Its thickness is zero. Set 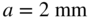 . Split the strip in the middle into two pieces that are connected at the ends. These two pieces are coupled to each other. Build a PEEC model for the strip composed of two partial inductances. Assume that the material is a Perfect Electrical Conductor (PEC) with a zero resistance. Hence, its resistance is zero. Use the closed-form partial elements given in Appendices C and D to compute the value of all components. Hint: The model has two partial inductance and four capacitive cells. Each partial inductance consists of an inductive half cell where they are sharing a node at each end.
. Split the strip in the middle into two pieces that are connected at the ends. These two pieces are coupled to each other. Build a PEEC model for the strip composed of two partial inductances. Assume that the material is a Perfect Electrical Conductor (PEC) with a zero resistance. Hence, its resistance is zero. Use the closed-form partial elements given in Appendices C and D to compute the value of all components. Hint: The model has two partial inductance and four capacitive cells. Each partial inductance consists of an inductive half cell where they are sharing a node at each end. - 6.2 Assemble circuit matrix using element stamps
Corresponding to the circuits in Fig. 6.8, assemble the circuit matrix (6.53) from the circuit equations using the MNA stamps in Appendix B.
- 6.3 Compute the impedance of a loop
A wire loop is shown in Fig. 6.11. Make a (QS)PEEC model for the loop and compute the loop impedance between A and B. Then remove branch 4 from the loop and compute the impedance of the open loop and compare the impedance results for the two cases. Also, check the impedance for using 1, 2, and 4 partial inductances per side. Use zero thickness sheet conductors of
 width for the model using equations (C.23) and (C.25). Assume that the square loop has a side length of
width for the model using equations (C.23) and (C.25). Assume that the square loop has a side length of  . Also compute the impedance of the loop arrangements if you also include the resistance of the conductors.
. Also compute the impedance of the loop arrangements if you also include the resistance of the conductors.
Figure 6.11 Single loop impedance example.
- 6.4 Impedance of loop with delays
Add delays or retardation to the loop impedance in Problem 6.3. This is accomplished by adding delays or retardation to the coupled partial inductances and the partial potential coefficients. The simplest way to do this is to assume that the delay can be computed from node to node for the partial potential coefficients. For the partial inductances, we calculate the delay from center to center of the cells and for the partial coefficients of potential we use the node-to-node delay. Make sure that you extend the highest frequency such that the added delay changes the result from the one obtained from Problem 6.3. Remember that for the highest frequency the cell size should be such that the wavelength of the frequency is such that the smallest wavelength is
 .
. - 6.5 PEEC circuit model for the external conductor
Assume that the current filament has a rectangular cross section with a width equal to
 and the height equal to
and the height equal to  . The length of the filament is
. The length of the filament is  and the current on it is uniformly along the longitudinal direction. Build the PEEC circuit model of this current filament by ignoring all couplings to other filaments possibly positioned nearby. Assume the material is copper with the conductivity
and the current on it is uniformly along the longitudinal direction. Build the PEEC circuit model of this current filament by ignoring all couplings to other filaments possibly positioned nearby. Assume the material is copper with the conductivity  and
and  . Use the closed form given in Appendices C and D to compute the value of all components.
. Use the closed form given in Appendices C and D to compute the value of all components.
References
- 1. S. M. Rao, D. R. Wilton, and A. W. Glisson. Electromagnetic scattering by surfaces of arbitrary shape. IEEE Transactions on Antennas and Propagation, 30:409–418, May 1982.
- 2. Y. Zhu and A. Cangellaris. Multigrid Finite Element Methods for Electromagnetic Field Modeling. John Wiley and Sons, Inc., New York, 8th edition, 2006.
- 3. A. Rong and A. C. Cangellaris. Comprehensive broadband electromagnetic modeling of on-chip interconnects with a surface discretization-based generalized PEEC method. IEEE Transactions on Advanced Packaging, 28(3):434–444, August 2005.
- 4. A. E. Ruehli. Electrical analysis of interconnections in a solid state circuit environment. In ISSCD, IEEE International Solid-State Circuits Conference, Volume XV, pp. 64–65, February 1972.
- 5. B. G. Galerkina. On the life and scientific career of academician B. G. Galerkin. Izvestiya Akademii nauk SSSR, Otdelenie tekhnicheskikh nauk, 8:1159–1164, 1951.
- 6. J. S. Hesthaven and T. Warburton. Nodal Discontinuous Galerkin Methods: Algorithms, Analysis, and Applications, Springer Texts in Applied Mathematics 54. Springer-Verlag, New York, 2008.
- 7. W. Pinello, A. C. Cangellaris, and A. Ruehli. Transient electromagnetic analysis and model complexity reduction using the partial element equivalent circuit formulation. In Massachusetts Institute of Technology, Volume 1, pp. 63–66, June 1997.
- 8. D. Hazony. Elements of Network Synthesis. Reinhold Publishing Corporation, New York, 1963.
- 9. G. Golup and C. Van Loan. Matrix Computations. The John Hopkins University Press, Baltimore, MD, 3rd edition, 1996.
- 10. N. Balabanian, T. A. Bickart, and S. Seshu. Electrical Network Theory. John Wiley and Sons, Inc., New York, 1969.
- 11. M. Celik, L. Pileggi, and A. Odabasioglu. IC Interconnect Analysis. Kluwer Academic Publishers, Boston/Dordrecht/London, 2002.


















