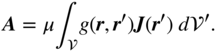Chapter 12
Incident and Radiated Field Models
In general, electromagnetic problems are of two fundamental classes – coupling or scattering. In coupling, coherent equivalent sources are generated on the surfaces and in the element volumes if two objects are in close proximity. In the partial element equivalent circuit (PEEC) formulation, we can subdivide the coupling into inductive and capacitive coupling. Further, resistive coupling can exist between galvanically coupled bodies. However, this type of coupling is usually absent unless the source and observation parts are part of the same system. In most systems, coupling will become stronger for higher frequencies.
The second class is scattering. If electromagnetic waves originate from a field, an object or body, and propagate to another object or interface with certain material property discontinuity, the energy will be distributed in various directions, which could be to infinity. This phenomenon is called scattering. While coupling is the key factor in circuits and some electromagnetic compatibility (EMC) applications, scattering is dominant in antenna designs, radar cross sections (RCS), and some important electromagnetic interference (EMI) issues.
Integral equation-based techniques, for example, Ref. [1] are favored for scattering and radiation problems since they automatically take care of open spaces without requiring other techniques such as absorbing boundary conditions (ABCs). Finite element methods (FEMs) [2] are another popular choice if the ABC or perfectly matched layer (PML) [3] is used to completely wrap up the radiating region.
The calculation of external fields and radiation for the PEEC method is accomplished for external field calculations with only a moderate additional solution effort. In its beginning, the PEEC method was primarily used for solving electromagnetic coupling issues. However, scattering or radiation problems have also been solved by the PEEC method.
For quasistatic problems, a SPICE circuit solver can be used for nonradiation problems to find currents and surface charge distributions. However, a separate equivalent component should be added for incident field and radiation computations. The computation of the external fields is essentially a postprocessing step once the current and charges or currents and potentials are computed.
Hence, the postprocessing of calculating the radiated field can be similar to that of conventional electric field integral equation (EFIE) formulations, especially if the low-frequency or dc solution is not important. We should note that, for example, the coupling to an antenna is a high-pass filter situation since low-frequency coupling between the source and the target object is absent.
In this chapter, we first consider the case of an external incident field impinging on a PEEC circuit. The first PEEC work in this area was done in Ref. [4]. Some early work on this subject was also done by M. Mandallena and by Pinello et al. [5].
We introduce two methods for the evaluation of the far-field radiation based on a solution obtained with a PEEC solver. The first one is based on placing artificial electric or magnetic sensors that extend the PEEC coupling concept to the far field. This was originated with the work in Ref. [6]. The approach includes the far-field sensors as part of the PEEC solving process. The PEEC model can include multiple field sensors – an approach that is presented in this chapter.
The second method is similar to the postprocessing used for conventional EFIE (3.67) solvers. Starting with the PEEC model solution vector, the radiated field is directly computed based on the auxiliary potentials. Far field approximation can be applied and the Sommerfeld radiation boundary condition can be clearly visualized from the results [7]. The radiation pattern can be computed from this process. This second method is more conventional than the first one.
Again, a key requirement for the modeling in this section is that we use full-wave (FW)PEEC models in Chapter 6, which include retardations or time delays. Neglecting retardation would not represent the far-field radiation, especially for higher frequencies above the quasistatic range such that the delays or retardation times are significant. Only the real part of the far field contributes to the far field radiation [14, 15].
We consider the derivation in the time domain. However, the solution method is fundamentally the same in the frequency domain. We start out with the electric field formulation (3.25) from Chapter 3,
where we simply can add a term for the case where finite dielectric bodies are involved in the model according to Section 10.4.5. Hence, the current contribution due to dielectric bodies can be added to the result.
In this chapter, we simply assume that the PEEC model solution has been set up according to Chapter 7 for nonorthogonal structures and in Chapter 6 for orthogonal structures. We simply add the parts of the models necessary for the incident and radiated field computations.
Figure 12.1 Example cell with component of incident field.
We should mention that radiation calculations have many applications in electronic systems such as, for example, to find the radiation from connectors [8]. Recently, more progress has been made in thecomputation of the radiated power [9, 10] and [13–15] using PEEC.
12.1 External Incident Field Applied to PEEC Model
We start this section with an independent external field applied in the presence of a PEEC model structure.
The new part of the incident field formulation is the collection of the electric field by the left-hand side of (12.1). Essentially, we need to add the source voltage along the inductive branch of the cell due to the incident electric field 
. We integrate the external fields over the cell shown in Fig. 12.1, or
where
These sources are simply added to the basic PEEC loop, which is an addition to the circuit based on part of the Kirchhoff's voltage law (KVL). Hence, it is obvious that the extension of a PEEC model with the electric field is straightforward (Fig. 12.2). The right hand side basic loop in Fig. 12.2 represents the PEEC model for a dielectric with the incident field applied.
Figure 12.2 PEEC model with voltage sources for an incident electric field.
In the modified nodal analysis (MNA) equations, the independent field sources will appear in the right-hand-side source vector of the MNA equations as shown in Fig. 6.10 and (6.55).
Figure 12.3 PEEC model with current induced by an incident electric field.
As an example, we experiment a simple problem that was solved using both PEEC [4] and an approximate transmission line solution [11]. The example problem consists of a two-wire transmission line, which is 1 m long and the conductors are spaced by 5 cm. The wires that are round with a diameter of 0.2 mm are in the PEEC model approximated with a zero thickness sheet cells with a width of 0.2 mm. Both ends of the transmission line are simply terminated with 
resistors.
For this problem, the result for the PEEC model is shown in Fig. 12.3 for three different numbers of subdivision along the length. As is evident, 
= 50 cells leads to a good solution up to 1 GHz. The incident field is in the 
-direction where 
.
12.2 Far-Field Radiation Models by Using Sensors
The computation of radiated fields emanating from a PEEC structure is important. Applications are the computation of radiated fields for EMI and antenna. As we mentioned in the introduction, the sensor technique first presented in Ref. [6], which is an interesting addition to the PEEC methods.
We evaluate the electric field with an 
-field sensor based on the PEEC EFIE (12.1) solution. We assume that no direct galvanic coupling exists to the location of the observation points. Then, we only have to evaluate the contributions of the inductive and capacitive terms, as is done in the following two sections.
We first want to remind the reader that we do need to include the delays, or the retardation times in the field calculations to the sensors. The delay time 
is the delay between the locations of the observation point 
and the source point 
, respectively. As considered in (2.11) for (FW)PEEC models
where 
is the speed of light.
12.2.1 Radiated Electric Field Calculations Using Sensors
The eSensor approach is based on work presented in Ref. [6]. An electric field sensor used for this approach is shown in Fig. 12.4. Essentially, the potential difference between two end points in the far field region is computed to find the field. Theevaluation of the field is based on the conventional orthogonal PEEC models in Chapter 6 and/or the nonorthogonal ones in Chapter 7. The sensor is located at a point 
, where the field needs to be computed. We only need to have three orthogonal sensors aligned in 
, 
, and the 
directions for the general case.
Figure 12.4 Electric field sensors for all three directions.
Further, a useful observation is that the sensor solution is independent of the rest of the PEEC model. Only a one-way coupling exists from the model to the sensors. This means that we can execute a PEEC solution independent of the sensor placement. Also, we can change the sensor locations to compute the field without the need to solve the problem again. Another positive issue for the solution is that multiple sensors, for different locations, do not interact with each other.
Another useful observation is that the structure of the coupling mechanisms from the PEEC circuit to the eSensor is similar to the coupling inside a PEEC model. Specifically, the partial element calculation facilities, which are part of the solver, can be used for the PEEC to sensors computations while the back coupling is set to zero.
The electric field sensors shown in Fig. 12.4 use three bars, one for the field in each direction. Since the method is the same for all three bars, it is sufficient to describe the sensor solution for 1 bar only. We chose the derivation for the 
-directed sensor for 
.
We should remember that the integral equation for PEEC is based on (3.25), which computes the 
-field. We use this to specifically compute electric fields, for the 
-directed sensor bar as
where the 
partial inductive coupling 
terms consider the inductive couplings to the 
-directed sensor element. The first right-hand side term in the field represents (12.1) is not coupled since we do not have a galvanic connection. Therefore, we did not include it in the sensor equations (12.5). If necessary, this term can be included directly in the field calculation.
12.2.2 Evaluation of z- Direction Inductive Coupling Term for the E-Field Sensor
The second right hand side term represents (12.1) the coupled voltage by the partial inductances. However, the very interesting situation is that we do not need a partial self-inductance coupling at the sensor to compute the inductively induced voltages. We must also compute the coupling to the 
-directed part of the sensor in Fig. 12.4 for the inductive coupled voltage to a zero thickness sensor filament of a length 
centered at the observation point 
in Fig. 12.4. This represents one branch for the coupling of a partial mutual inductance.
The contribution of the inductively coupled voltage from the cell 
to the sensor is similar to (6.9) as
where 
is the current in the 
-directed partial element of the PEEC model. We recognize that the integrals on the right-hand side represent the coupling using the contribution by a partial inductance coupled to a 
-directed filament representing the sensor.
The remaining issue in (12.6) is the computation of the time derivative of the transient currents 
. Details for an accurate time domain solution are considered in Section 2.4.
For the time domain 
-field computation, we have a postprocessing step since all the currents are already precomputed in the solution. Following the notation in Section 2.4, we call the present time step 
as usual for which the solution has been obtained. The solution at the present time step 
which is given by 
, where 
is a uniform time step.
To create a simple example, we assume that the delay from the inductive PEEC cell to the eSensor origin 
is 
. Then we can compute the current derivative as
If the delay is not a multiple of the step delay 
, the linear interpolations can be used. Note that these issues are the same as the updating of the right-hand-side elements for the time domain MNA equation solution (2.28) for systems with delay.
The computation of the delayed currents in the frequency domain is rather straightforward. The equivalent of (12.6) in the frequency domain can be approximated as
where 
is the same delay as in the time domain. Recognizing that we can use a partial inductance that couples to the filament in Fig. 12.4, (12.8) can be simply evaluated as
It is clear that, in general, the length of the sensor 
is chosen to be small compared to the shortest wavelength 
, like 
. But on the other hand it shall be large enough not to lead to numerical errors.
If finite dielectric bodies are present as considered in (10.62), the currents and the inductive couplings also need to be taken into account in exactly the same way. The equations for the contributions 
for the dielectrics are the same as (12.6) for the time domain or (12.9) in the frequency domain. This is due to the fact that finite dielectric models also include partial inductances.
12.2.3 Potential Coefficient Coupling Contribution
We evaluate the last part in (12.5), 
. The electric field part of the sensed field is given by
where the potential evaluation points are shown as squares at the ends of the sensor in Fig. 12.4. The gradient is found by evaluating the potential 
at the two end point squares of the sensor. The gradient is numerically approximated as
We note again that the sensors only involve mutual couplings. We have to establish a coupling mechanism from all the capacitive cells in the PEEC model to evaluate the potentials 
at the two end points. To accomplish this, we have to compute the coupled potentials based on Section 6.3.4 for the 
capacitive cells in the problem at hand:
and
where the delays 
and 
both are the delays from the capacitive PEEC cells to the eSensor squares. Here, the sums include all the capacitive cells in the problem. This includes all the contributions necessary for the 
-field computation in (12.14) or (12.15).
It is evident that we need to add all the contributions from each of the terms of the equation to get the total 
-field. This has to be done at each time point and the contributions at field sensor observation point 
are found. Again, summing up all potentials will lead to the total radiated 
-field.
12.2.4 Summary of 
-Field Calculation with eSensor
Finally, all the components have been prepared for the 
-field sensor. This leads to the following equation for the field evaluation:
where the potentials are evaluated at each end of the sensor filament. The 
-field in the frequency domain is very similar to the time domain. Essentially, we need to transform (12.14) to the frequency domain for the direct evaluation of the field to get
where the delays are given by the physical location of the sensors. It is clear that the evaluation of the 
-field in the frequency domain is similar to the time domain since the same small dipole arrangement is used at the observation point 
.
12.2.5 Magnetic Field Calculation Using Sensors
The magnetic field (
-field) is calculated differently from the 
-field in the previous sections. There are several ways to compute the 
-fields where some of them do not lead to reliable numerical results, or where they do not work well for a wide frequency range. The hSensor approach we present is also from Ref. [6]. It is based on utilizing partial inductances from the PEEC model.
In Fig. 12.5, we show the hSensor, which consists of three small field test loops, where the total field is
Each of the loops senses the field for one of the orthogonal directions. They measure the field at the observation point 
. We again assume that the sensors are small compared to the smallest wavelength in the spectrum.
Figure 12.5 Magnetic field sensors loops for all three directions.
12.2.6 Time Domain Solution for 
-Field Sensor
We assume that all sides of the sensor arrangements in Fig. 12.5 are the same, 
. Since all three loops are fundamentally equivalent, it is sufficient to consider a single loop to illustrate the approach. Our example is a loop in the 
–
plane to compute 
shown in Fig. 12.6.
The voltage induced in the loop from the PEEC circuit is
where the normal component of 
is integrated over the area 
of the sensor loop. With 
given by (3.1d), we can solve (12.17) for 
where the induced unknown voltage time integral of 
in Fig. 12.5 needs to be computed to find 
.
Thin filament conductors are used to form the loop in Fig. 12.6 for the computation of the coupled induced voltage. To compute the total induced voltage for the 
-loop in the example Fig. 12.6, we need to compute all partial mutual inductances that couple from the inductive PEEC cells in the problem to the loop filament conductors. Of course, the couplings are direction dependent and can be sparse, especially for rectangular Manhattan problems. Then, the voltage induced in test loop in Fig. 12.6 is
where the sum is over all conductors 
that are not orthogonal to the sensor filament considered. All three components of the field in (12.16) can be computed.
Figure 12.6 Example 
-loop for inductive coupled voltages.
We observe that all sensors do not involve partial self-inductances. Hence, sensors do not have an impact on the solution and the above techniques can be applied as a postprocessing step once the solution vector 
is known. Rectangular loops can always be used even if the rest of the problem consists of nonorthogonal cells.
12.2.7 Frequency Domain Solution for 
-Field Sensor
We consider the time domain computation 
and the frequency domain computation 
. We note that the key equation (12.18) can easily be transformed into the frequency domain to
since integration in the time domain is equivalent to the division by 
in the Laplace domain. Due to the 
behavior, it is clear that the application for low frequencies loses accuracy.
All the other solution steps are the same as that of the time domain solution in the previous section. Of course, the coupling (12.19) with retardation transforms to
Finally, the computing of the contributions by the sides of the loop in Fig. 12.5 are very similar in both domains. In the frequency domain, we utilize the calculated currents at each frequency in a straightforward way. This is in contrast to the time domain, where we utilize all the current waveforms from the transient analysis over the time interval.
12.3 Direct Far-Field Radiation Computation
In this section, we present the second approach for the computation of far fields at points outside of the structures. This approach is easier to apply in the frequency domain rather than in the time domain. We start the derivation assuming that a single frequency time harmonic field in air at an angular frequency 
or a wave number 
is applied as considered in Section 3.4.1.
12.3.1 General Radiated Field
Following the formulations in Chapter 3, the magnetic field can be represented by (3.18) based on the auxiliary vector potential
and the electric field (3.22) using also the scalar potential
where the vector potential can be generally computed from the currents from the PEEC solution vector as (3.50)
The scalar potential (3.52) is calculated from the solved charge distribution (3.52)
where 
is the usual free space Green's function (3.63)
where 
and 
.
Based on the gradient of Green's function
by using (12.27) and (12.24) in (12.22), we find
or
which is based on [7]. From this equation, it is clear that the far field 
can only have the tangential components relative to the longitudinal direction 
. At infinite, according to the Sommerfeld radiation boundary condition [7], the radiated waves are plain waves. Hence, the electric field will also have tangential components only.
Even though the electric field intensity can be computed directly based on (12.23), it is more consistent by using Ampere's circuital law at the observation position to avoid any numerical inconsistency between the computed current and charge distributions. In the frequency domain, at the field observation point where 
, we have
We can compute the electric field 
by substituting (12.28) into (12.30).
12.3.2 Radiated Field Computation Based on the PEEC Computation Results
For the solution we use for weighted residuals method (WRM) approach, where the capacitive cells have the conventional constant charge density. The currents in rectangular cells are in one direction. Therefore, the current in each inductive cell is constant in both value and direction. Therefore, if the cross section of the filament is 
and its length is 
, the resultant current and the currentdensity in this rectangular filament is 
. The current 
is a vector with a given direction. Assuming that the problem has a total of 
inductive current cells and we apply the discretization to (12.28), we have
where 
is along the longitudinal direction of the cell filament. Based on this assumption, the current density is replaced by the current for the constant current density in each cell. Accordingly, the electric field can be computed similar to (12.30) and (12.28).
Figure 12.7 Example of approximation for far-field computation.
12.3.3 Approximate Computation of Far Fields
As shown in Fig. 12.7, 
is a vector to the distant observation point location. A condition for a far-field approximation is that the observation point is far in comparison to the relative size of the object 
. Also, the wavelength 
is assumed to be smaller than 
. On the other hand, the point vector 
for a point on the object close to the origin is much smaller than r. We call the angle at the origin 
. Under these assumptions, it is possible to use the far-field approximation to simplify the field calculation [12]. It is well known from the geometry that we can approximate the distance 
as
The condition for the approximation to be applied can be expressed as
where again 
is the length of the vector 
and 
is the maximum dimension of the radiator model. We can use it in (12.28), considering the fact that at infinity 
, 
, 
. We can assume that the components of the far field such as the 
or higher order term decay fast and can be ignored. This results in
where starting from (12.26) Green's function used is
An approximation can be obtained for the far field starting with (12.23). The scalar potential primarily contributes to the longitudinal field components, while it cancels the contribution to the longitudinal components of the vector potential. Hence, we only need to compute the tangential components of 
to approximate the far field of 
. As a result, the far field of 
is derived to be
By taking the ratio of 
, we can find the intrinsic impedance 
. It is understood that the solution is a plain wave satisfying the Sommerfeld radiation condition at 
[7].
Problems
- 12.1 External incident electrical field
We assume that an electric field is incident to a PEEC cell in the
–
plane. Explain and formulate the contribution of the external incident electric field and derive the equivalent circuit source. Consider both the polarization and the orientation of the wave compared to the orientation of the mesh cell. - 12.2 Circular polarization incidence
Derive the PEEC model when the external incident wave is a circularly polarized plane wave.
- 12.3 Dipole radiation field
Assume that a half-wavelength dipole is made of two strips that are perfect electrical conductors (PECs) of zero thickness. The length of the dipole is 1.5 m. Compute the radiated magnetic field at a distance of
at a frequency of 300 MHz using the electric field sensors introduced in Section 12.2. - 12.4 Loop radiation field
The problem consists of a square loop with an edge length of 1 m. The cross section of the loop is
being a PEC. Compute the radiated magnetic field at a distance of 50 m at a frequency of 300 MHz using the magnetic field sensors introduced in Section 12.2. - 12.5 Far-field zone
The approximate computation of the far field is given in Section 12.3.3. In the derivation, the formula (12.34) is given. Give an explanation of the physical meaning of the far-field zone limit given in this equation.
References
- 1. R. F. Harrington. Field Computation by Moment Methods. Macmillan, New York, 1968.
- 2. J. M. Jin. The Finite Element Method in Electromagnetics. John Wiley and Sons, Inc., New York, 2nd edition, 2002.
- 3. A. Taflove Ed. Computational Electrodynamics. Artech House, Inc., Norwood, MA, 1998.
- 4. A. E. Ruehli, J. Garrett, and C. R. Paul. Circuit models for 3D structures with incident fields. In Proceedings of the IEEE International Symposium on Electromagnetic Compatibility, Dallas, TX, pp. 28–31, August 1993.
- 5. W. Pinello, A. C. Cangellaris, and A. Ruehli. Hybrid electromagnetic modeling of noise interactions in packaged electronics based on the partial-element equivalent circuit formulation. IEEE Trans MTT, Volume 45(10):1889–1896, October 1997.
- 6. G. Wollenberg and A. Görisch. Analysis of 3-D interconnect structures with PEEC using SPICE. IEEE Transactions on Electromagnetic Compatibility, 41(2):412–417, November 1999.
- 7. W. C. Chew. Waves and Fields in Inhomogeneous Media. IEEE Press, New York, 1995.
- 8. B. Archambeault, S. Connor, M. S. Halligan, J. L. Drewniak, and A. E. Ruehli. Electromagnetic radiation resulting from PCB/high density connector interfaces. IEEE Transactions on Electromagnetic Compatibility, 55(4):614–623, August 2013.
- 9. J. Nitsch, F. Gronnwald, and G. Wollenberg. Radiating Nonuniform Transmission-Line Systems and the Partial Element Equivalent Circuit Method. John Wiley and Sons, Inc., New York, 2009.
- 10. Y. S. Cao, L. J. Jiang, and A. E. Ruehli. Distributive radiation and transfer characterization based on the PEEC method. IEEE Transactions on Electromagnetic Compatibility, 57(4):734–742, August 2013.
- 11. R. T. Abraham and C. R. Paul. Coupling of electromagnetic fields to transmission lines. In Proceedings of the IEEE International Symposium on Electromagnetic Compatibility, pp. 164–170, August 1981.
- 12. C. A. Balanis. Advanced Engineering Electromagnetics. John Wiley and Sons, Inc., New York, 1989.
- 13. L. K. Yeung and Ke-Li Wu. PEEC modeling of radiation problems for microstrip structure. IEEE Transactions on Antennas and Propagation, 61(7):3648–3655, July 2013.
- 14. C. C. Chou, W. C. Lee, and T. L. Wu. A rigorous proof on the radiation resistance in generalized PEEC models. IEEE Transactions Microwave Theory and Techniques, 64(12):4091–4097, December 2016.
- 15. Y. S. Cao, L. J. Jiang, and A. E. Ruehli. Distributive radiation and transfer characterization based on the PEEC method. IEEE Transactions Electromagnetic Compatibility, 57(4):134–142, August 2015.