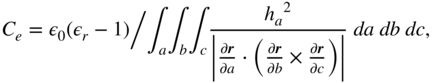7.1 Representation of Nonorthogonal Shapes

It is clear that one of the more complicated parts for the nonorthogonal shape modeling is the coordinate system that represents the geometry. This is an important part of this chapter.

A few concepts are fundamental for the treatment of nonorthogonal shapes. First, the global coordinate system determines the location of all objects independent of their local orientation. This global coordinate system is a conventional, orthogonal one where an object is assumed to be located at a point . How can we then represent an object with an arbitrary orientation? In general, this local object can be an orthogonal, quadrilateral, and/or hexahedral conductor or dielectric block or cell. Hence, we need to define the center point of the th object and its orientation with respect to the general coordinates.

In the global orthogonal coordinates, a vector from the origin to the point is given by where the global unit vectors , and are position independent. To emphasize the vector represents always the global coordinate system. However, a typical case has many local coordinates for the many nonorthogonals subsystems that are represented with different orientations in the global system.

It is important to understand that each separate local coordinate system is locally coupled to the global coordinates. Hence, the local coordinates allow the arbitrary orientation of the local objects. We call the local coordinates . We use to distinguish them from circuit variables such as voltage . It is clear that we need to relate the local coordinates to the global ones.

We start out with the description of the geometrical objects that can be orthogonal and/or nonorthogonal. The more difficult issue is the representation of nonorthogonal geometries. The global coordinate system represents all parts of the geometry. Ultimately, all bodies need to be described in global coordinates such that the interactions can be represented.

A simple nonorthogonal example is the case where a straight wire connects between and , which is shown in Fig. 7.2. For example, we would like to represent the global coordinate in terms of the local coordinate variable . Then, we can represent all points in between the two end points and as

7.1

by choosing a point where . It is evident that if , then and if then .

The local unit vectors are defined as , , and . Details about nonorthogonal coordinate systems can be found in several texts, for example, Ref. [19]. Figure 7.3 shows an example of a zero thickness quadrilateral element with its local coordinate system. For example, we need to be able to specify the location of points on the surface of the quadrilateral. In this text, we assume that all local cell surfaces for all objects such as quadrilateral as well as hexahedrons are planar. From Fig. 7.3, it is clear that the quadrilateral is uniquely defined by the coordinates of four plane corner points. This introduces a linear dependence of some of the coordinates. The global coordinate center point is at the origin of the local coordinates shown in Fig. 7.3.

Next, we present a simple approach for a unique definition of the corners of the local coordinates in the global system. This is accomplished in a clever way by the local variables where and as will be given below. Based on Fig. 7.3, the corner location corresponds to or and or . Hence, it is convenient to use logical variable to identify the corners. We assign a logical zero to the variable and a logical to the variable , and so on. Hence, Table 7.1 can be constructed for the corner representation.

Variable	Variable	Logic	Logic	Corner assigned
		0	0	0
	1	0	1	1
1		1	0	2
1	1	1	1	3

From this, it is easy to uniquely assign logical codes to the corners in Fig. 7.3.

With this definition of the corners, we can uniquely relate the location of a point on the quadrilateral surface to a point in the global rectangular coordinate system . This is accomplished by the following conventional mappings:

7.2a

7.2b

7.2c

7.2d

and

7.3a

7.3b

7.3c

where () is located on the quadrilateral surface and () is the corresponding point in the global coordinates.

7.1.1 Hexahedral Bodies

It is clear that for many partial inductance and resistance cells and dielectric bodies, etc., we need finite thickness cells. For this case, we need three coordinates () to describe a point, where is added to the quadrilateral sheet representation as shown in Fig. 7.4. Clearly, the model is an extension of the quadrilateral case. We only have to add the equations for the three local directions.

First, the corner assignment for eight corners is shown in Table 7.2.

Logic	Logic	Logic	Corner assigned
0	0	0	0
0	0	1	1
0	1	0	2
0	1	1	3
1	0	0	4
1	0	1	5
1	1	0	6
1	1	1	7

The coefficients for (7.5) are given by

7.4a

7.4b

7.4c

7.4d

7.4e

7.4f

7.4g

7.4h

where all the local coordinate variables are between . Because node indices are unique, again we can obtain the mappings to the global coordinates as

7.5

At this point, we have a unique mapping between a local point located anywhere in the hexahedral shape to the global coordinates . The combined coordinate systems represent a convenient way to represent nonorthogonal coordinates for the shapes at hand.

7.1.2 Derivatives of the Local Coordinates

Hopefully, it is clear now that local coordinates pertain to a specific body. The local variables are valid only on the surfaces or inside the volume of the body. The main purpose of the local coordinates is to facilitate the evaluation of PEEC circuit elements the nonorthogonal partial inductances, potential coefficient, and the resistances. For these computations, we notonly need relations between the global coordinate vector and its local coordinates but also local derivatives for the local coordinates and other information.

For example, for a quadrilateral shape in Fig. 7.3, we can simply find the general derivatives

7.6a

7.6b

7.6c

7.6c

Based on (7.3), we can obtain the desired derivatives using (7.6a)–(7.9)

7.7a

7.7b

7.7c

where the other two sets of derivatives with respect to and are specified by replacing by or . We finally have all the components for the evaluation of the important tangential vector with respect to the local coordinates that are

7.8

The importance of these derivatives is evident in the following section.

7.2 Specification of Nonorthogonal Partial Elements

The derivations of the vectors in the previous section provide the foundation for the formulation of the nonorthogonal partial elements. For the partial coefficients of potential , zero thickness rectangular or quadrilateral shapes are used since the charge is a surface quantity. For resistances and partial inductances , rectangular or hexahedral boxes are used. As a practical solution for uniform thin partial inductances or resistance, we can utilize quadrilateral shapes with a uniform thickness without having to resort to more complex hexahedral representations. It is clear that we want to use nonorthogonal coordinates only where it is necessary. For example, for the coupling between a rectangular and a nonorthogonal shape, we represent each shape with the appropriate coordinates. Of course, we can adhere to the global rectangular coordinates for the rectangular Manhattan object.

We use a zero thickness or very thin quadrilateral conductive sheet shown in Fig. 7.5 to motivate the derivation of the next step. An inductive/resistance half cell between nodes 0 and 2 is illustrated on the quadrilateral shape with the current density vectors. Further, the crosshatched area attached to node 1 is an example of a capacitive quarter cell. We recognize that in both cases, full cells can be formed by attaching other sheets to the same nodes forming larger bodies. As an example, two inductive half cells from two different quads can be connected between nodes 0 and 2 and four capacitive quarter cells may be connected to node 1 to form full capacitive cell.

The direction of the current flow in Fig. 7.5 from node 0 to node 2 is given by a vector that changes direction with position on the half cell. We can compute the tangential direction vectors , , from the tangential vector by first forming the magnitude of the vectors

7.9

The unit vectors are found by dividing the vectors by the magnitude, or

7.10

These unit vectors give the direction of the current anywhere on the cells.

For completeness, we also want to introduce that the square of the magnitude is also called the metric coefficient [19]. For example,

7.11

7.2.1 Discretization of Conductor and Dielectric Geometries

Chapter 3 shows the integral equation representing the solution to be discretized, for example, (3.54) for orthogonal structures whose solution is given in Chapter 6.

The basic hexahedral element or object for the nonorthogonal element is shown in Fig. 7.4 and an example for the connection between quadrilateral and orthogonal surface elements is shown in Fig. 7.6. As we do for rectangular coordinates, we set up the inductive and capacitive meshes. For example, we see how the quarter cells connected to the node form the capacitance plate. However, it is clear that the total cell potential coefficients are also computed by combining the quarter cell values. The inductive cells are formed by half cells or by combining two half cells into a full cell. To represent thecurrent flow in the orthogonal cells, we use the conventional current density or weighting function , where and are the current and current density while and are the cell width and thickness, respectively.

For the nonorthogonal case, we assume that the conductor thickness is also subdivided into cells. As an example, the thickness divisions take the skin effect into account as considered in Chapter 9. This leads to the hexahedral elements in Fig. 7.4 for the nonorthogonal case. It directly leads to a nonorthogonal version of the volume filament (VFI) skin-effect model presented in Section 9.3 especially for conductors with a constant thickness.

The generalization of the current distribution weighting for nonorthogonal hexahedral cell shapes is given by

7.12

where and can easily be found by permuting the indices. We call the quotient in (7.12) the weight so that it is simplified to . We shall note that all the above quantities are a function of the local position coordinates .

Next, we use an integral or inner product operator that essentially implements for the nonorthogonal case, or

7.13

Where is the field term to be integrated. In fact, we need to apply the inner product to each term of (3.54) to transform each term to a voltage drop across a PEEC circuit element in the Kirchhoff's voltage law (KVL) equation.

The first element on the right-hand side terms (3.54), equivalent to the derivation for rectangular coordination in Section 6.1, leads to the series resistance term in the form

7.14

To give a specific example of a resistance case, if we consider the cell between corners 0 and 2 in Fig. 7.5. The resistance connected to corners will be

7.15

where we assign a uniform thickness to the layer in the direction.

The second right-hand side term of (3.54) yields the partial inductance corresponding to (5.17). The orthogonal Manhattan case is repeated here for convenience:

7.16

For the nonorthogonal case, after applying (7.13) becomes the generalization of the partial inductance concept for nonorthogonal problems, or

7.17

where the Green's function still is evaluated with the same global coordinates and . This clearly makes the analytical evaluation of the integral more difficult in the nonorthogonal coordinates. We also want to give a specific example for the evaluation of the integral for the quad sheet in Fig. 7.5. In this case, also assume a small thickness in the direction where we compute the partial mutual inductance between the half cells with corners (0,2) and (1,3), which is

7.18

The dot-product in (7.18) can be evaluated in several different ways depending on the details of the integration techniques used in Appendix C. Also, as an approximation we may evaluate the unit vectors at the center of each of the half cells.

The charge density is of a similar form as (7.12). Of course, the charge does not have a directional dependence. The volume charge density is given by

7.19

where is the total charge in the volume cell. For conventional conductors, the charge is located on the surface cells only. The gradient of the potential in the direction is evaluated to be

7.20

To maintain the symmetry for the circuit elements or coefficients, we approximate the derivative using an integrated average over the two corner cells corresponding to the derivative where the spacing is the projection in the direction for the center-to-center distance . This approximation implies that (7.20) can be simplified to

7.21

where is a surface in the appropriate surface direction.

Finally, by substituting for the potential as in (3.58b) into (7.21) and by canceling the appropriate terms, we get for the normalized coefficients of potential

7.22

where the global coordinates and are evaluated on the cell related to the cell of interest.

We also want to give an example for the evaluation of a . In Fig. 7.5, we chose the capacitive quarter cells, one is the crosshatched attached to corner 1 and to the quarter cell attached at corner 2.

7.23

The PEEC circuit for a quadrilateral element is shown in Fig. 7.7. It consists of basic KVL loops. Specifically, a KVL loop involves two nodes with a partial inductance and a resistance in series that is closed by the capacitances to infinity. As is evident from Fig. 7.5, the part of the model represented by Fig. 7.7 includes the inductive half cells and the capacitive quarter cells.

Of course, we can simplify neighboring quads with some partial elements that are connected to the same nodes in parallel. Specifically, the two inductive half cells connected to and in Fig. 7.6 could be combined. Again, the PEEC circuit topology for the orthogonal and the nonorthogonal cases are the same, with the exception of the circuit element values and the additional partial mutuals. Importantly, the same modified nodal analysis (MNA) circuit solver can be used for all cases.

Using the excess capacitance model in Section 10.4.6, we can also treat dielectric hexagonal blocks. The fundamental formulation is same for both situations. Similar to the orthogonal case, the dielectrics are represented with the same circuit elements. Using the nonorthogonal excess capacitance of a dielectric cell that is equivalent to (10.68) as

7.24

where is the dielectric constant of the dielectric cell. The equivalent circuit shown in Fig. 7.8 for the dielectric excess capacitance model is copied for convenience from Fig. 10.18. Importantly, we simply can take the nonorthogonal partial inductance in (7.17) and the series resistance in (7.14). The details of the derivation are given in Section 10.4.6.

7.2.2 Continuity Equation and KCL for Nonorthogonal Geometries

The continuity equation for the rectangular PEEC models is considered in Section 6.3.1. The continuity equation must also be satisfied for the nonorthogonal case at the cell level for the currents and charges. Its differential form is given by (3.3) or where again is the current density and is the surface charge density. The continuity equation needs to be applied at the location of each node corresponding to Figs. 7.3–7.5.

Unlike in Fig. 6.3, for the model we only show a quarter of the area in Fig. 7.9 for which the continuity equation is applied. Here, we show only one quarter of the centre cell unlike in Fig. 6.3, which shows the cell for rectangular coordinates. Since only one quarter of the elements surrounding the node is shown, we assume that the surface element in Fig. 7.9 may be connected to other similar surfaces along the – and the – surfaces. Hence, the volume for which the continuity equation is applied consists of the corners that are involved in the geometry surrounding the node(s). It is sufficient to consider only the corner elements by ignoring the internal surfaces shown in Fig. 7.9 for simplicity.

Integrating the continuity equation over the corner yields

7.25

where the divergence theorem (3.33) [20] is used in the last step and the vector is normal to the surface . The volume integral part pertains to the charge on the top and bottom surface corners connected to nodes 1 and 0, which are charged as indicated with in Fig. 7.9. If the nodes 0 and 1 are shorted, then the charge density consists of two -functions at the surfaces of the conductors with the surface charge and the contributions at are

7.26

and where the surface charge can be found from (7.19) as . Substituting this into (7.26) yields the charges on the corner surfaces.

Similarly, the currents associated with the corner nodes 0,1 are flowing through the cross-sectional areas indicated by in the direction and in the direction. The current through the section of conductor cross section for is given by

7.27

Where is given by (7.12).

Again, the same relationship holds for the equation for the coordinate. Adding all terms pertaining to the continuity equation, we get for one corner only

7.28

which can be recognized as the Kirchhoff's current law (KCL). It is evident that the continuity equation is satisfied since the admittance part of the MNA [21] formulation method is based on summing up all the current contributions at a node. Since the partial inductances extend from one node to a neighbor node, we need to subdivide the partial inductances into two halves where the part at the node is instantaneous and where the second part which belongs to a neighboring cell must include retarded partial mutual inductances.

7.3 Evaluation of Partial Elements for Nonorthogonal PEEC Circuits

For nonorthogonal geometries, the partial element evaluations are more challenging. In all cases, the singular Green's function is more difficult for the partial self-terms. Of course, the singularity can be eliminated if an analytic integration is possible.

The nearest neighbor results in coupling elements that are largest in magnitude. Therefore, these coefficients usually require more care. The magnitude sensitivity decreases with the distance between the cells for the partial elements. However, this is not the case for the radiation or phase sensitivity that is almost the same for all distances between the cells.

The partial element evaluation represents an important part of the overall solution. For this reason – and for the efficient evaluation of all elements – the so-called multifunction approach was devised, which is outlined in Appendix E. Issues of importance are both the accuracy and speed for the partial element evaluation. A general evaluation of partial elements for nonorthogonal structures consists of the combination of analytic and numerical techniques. Some of the formulations are presented in Appendices C and D.

We consider an example for partial element evaluation using a mixed numerical–analytic combination. The example involves a quadrilateral cell problem where the thickness is represented by a set of layers or sheets as shown in Fig. 7.10. In this example, the thickness of the 3D hexahedral structure is assumed to be thin compared to the other cell dimensions. Hence, the numerical integration is applied in the thin direction as shown with the sheets in Fig. 7.10.

If we use local coordinates, the th sheet is specified by , , and . The values of the are the values obtained from the Gaussian quadrature rule for the levels. Hence, each inductive cell is represented by four sheets as is shown in Fig. 7.10. There are thus a total of four sheets for each inductive cell shown in Fig. 7.10. The value of determines the accuracy for a given aspect ratio of the cell and the accuracy required.

For the inductance computation, the partial inductance of each sheet cell is required with respect to all the other sheet cells. Importantly, the integral (7.17) is reduced to the evaluation fourfold integrals of the following form

7.29

where is the product of the number of layers represented by each of the two cells. The partial inductance problem is reduced to a fourfold integral with the surface subdivisions that is easier to evaluate even if numerical integration is used.

As an example, we can use rectangular or triangular subcells to compute the self- or mutual value for two cells. The important issue is that at the PEEC level, we still want to use rectangular, quadrilateral, or hexahedral cells. Assuming that we subdivide a local coordinate sheet into subcells, then we have subdivisions that are chosen to maintain a reasonable aspect ratio as well as the required accuracy. Fortunately, analytical formulas also exist for the evaluation of quasistatic triangle surface integrals such that the singularity can be avoided [24]. The integral over the smaller of the two cells can be performed numerically.

As another example, the integration in (7.17) with respect to and can be performed by using a nine-point sixth-order accurate product Gaussian quadrature rule. Once we have obtained an approximation to the integral (7.17) using this method, we divide each cell into twice as many layers as before, by doubling , and repeat the procedure, obtaining another approximation, . Then, we can use a second- order Richardson extrapolation to obtain our final estimate [22, 25].

Analytical formulas are available for rectangular shapes. Therefore, it is always desirable to use as many rectangular cells as possible. But it is also possible and actually convenient to use Gaussian quadrature for rectangles when accuracy is not critical. For example, for the far distance interaction for the static field, the Gaussian quadrature rule can achieve convenience and satisfactory accuracy without excessive compute time.

If triangles are used, most calculations are performed in the numerical regime. Gaussian quadrature rules as shown in Appendix E will be a convenient facility to handle the integrals.

The overall integral can lead to a time-consuming evaluation for too many subdivisions. Hence, we would like the number of subareas as small as possible. The compute time and accuracy are the key issues why this is such an important issue. Hence, the evaluation of the integrals is predominantly performed analytically, given the techniques in Appendices C and D. In the example in Fig. 7.11, results in a partial self ( or ) double integral, which leads to the following two integrations over the subareas

7.30

Assuming that we want to compute a self or for the example in Fig. 7.11, we set . We want to point out that the practical evaluations of (7.30) can be simplified due to the symmetry of the subintegrals and other issues if some shapes are the same. If we have to compute the partial mutual or , we can take advantage of the symmetry of the coefficients.

We note that the subdivision of the cells into subcells allows the additional refinement of the phase by the assignment of the local retardation in the time and frequency domains. Only a small amount of additional compute time results since the subcells are located on the same cell without introducing additional element in the MNA unknown vector. This serves as phase refinement that is used in the passivity enhancement techniques as presented in Section 13.5.2.

The techniques presented in this chapter results in a refined solution for nonorthogonal shapes with large aspect ratio cells.

7.3.1 Analytic Solution for Quadrilateral Cells in a Plane

In this section, we present the analytical evaluation of the zero thickness integrals for quadrilateral cells located on a plane. This derivation would be too lengthy for the Appendices C and D. In addition, there are other results that are useful such as the integral over filament with the kernel . The integrals are complicated in spite of the fact that they do not have singularities in the integrand. Remember that the original integrals have singularities for the self-terms. In this section, we are using global coordinates for the evaluation of the integrals since an analytic result can be obtained in global coordinates for this case.

The original work was presented in Ref. [23], whereas the new solution was led by D. Romano in a recent work. The evaluation of the partial potential coefficient using local coordinates is given by (7.24). A self-term for a quadrilateral cell is shown in Fig. 7.12 and the coupling situation for two quadrilateral cells is given in Fig. 7.13.

We observe that the key difference between the partial coefficients of potential and the partial inductances is a different multiplication factor as well as the dot-product between the current directions. We have to approximate the dot-product for partial inductances by using average current directions. However, the accuracy is reduced if the current direction changes considerably over at least one of the cells. This may require further subdivisions of the cells.

The geometry of the problem of interest is shown in Fig. 7.13 for the general case for two quadrilaterals, whereas Fig. 7.12 represents the special case for the self-term. In this computation, we have to assume that both surfaces are located in the plane in the general coordinate system . The two zero thickness quadrilateral cells 1 and 2 are specified using the local corner coordinates 0–3, with the associated global coordinates with the surfaces for quadrilateral 1 and for 2 corresponding to the primed coordinates. The integral to be evaluated for the zero thickness or is

7.31a

with

7.31b

where and denote the source and observation points on and . For the two generic quadrilaterals and , the following identity holds [24]:

7.32

where and are the surface operators, and where the second one operates on the primed coordinates, respectively. By means of the surface gradient and the surface divergence theorem [19], (7.31a) is transformed to

7.33

where and represent the circumferences of the quadrilateral shapes. We should repeat that they are in the plane. Also, and are the outward vectors normal to and as shown in Figs 7.12 and 7.13. They are related to the unit vector tangential to the quadrilateral sides and and they are normal to their surfaces unit vector , by means of

7.34a

7.34b

Application of (7.33) to and gives a 16-term sum of line integrals

7.35

Since the sides of the quadrilaterals are straight lines for each pair of sides and , then each term of (7.35) becomes

7.36

The analytical integration of integrals depends on the configuration of two sides and .

If the two sides are perpendicular where , then the computation of is zero. Hence, removing the evaluation saves compute time. Of course, the and axes are exchanged if the integration is set up in the wrong direction. The analytical evaluation of is considered in the following section for the general case as well as the special case when two sides coincide is considered.

7.3.2 General Case for Evaluation of Integral

It is clear from the previous section that to evaluate , we have to solve the integrals between two segments and as shown in Fig. 7.14. Hence, the integrals involve two lines with the end points , and with the end points and , which can substitute from (7.35) in the global reference system for as

7.37

and for as

7.38

Substituting (7.31b), (7.37), and (7.38) in (7.36) one obtains

7.39

In (7.39), the internal integral is solved by using the formula (7.56a)

7.40

where it is defined that

7.41

Substituting (7.40) in (7.39) one has

7.42

The integrals for on the right-hand side of (7.42) refer to the four terms shown in (7.40). These four integrals are evaluated next.

For which is

7.43

by substituting in the first and the last equations of (7.37)

7.44

where

7.45

The integrals in (7.44) are solved by using the formulas (7.56 a) and (7.56 b).

Following the same steps, an expression for is obtained, which is the same as in (7.44). The only difference is in the expressions for the coefficients , and , which are equal to the ones in (7.45) if is substituted by .

For

7.46

by substituting in the first and the last equations of (7.37)

7.47

where

7.48

In the above expressions, the coefficients , , and are given in (7.45). In order to further simplify the analytical solutions of the integrals of (7.47), it is possible to set that can be written as

7.49a

7.49b

7.49c

with

7.50

We should exclude from the solution for , which results for the case when the two segments are perpendicular. For this case, the evaluation of is eliminated as mentioned in Section 7.3.2. The analytical solution for the integrals , , and is given in (7.56) and (7.58).

Following the same steps, the expression for is obtained: it is completely equal to that for in (7.47). The only difference is in the expressions of the coefficients , , and that are equal to those in (7.45) and (7.48) with substituted by .

7.3.3 Evaluation of Integral When Two Sides Coincide

For two sides coincident, equation (7.38) can be written as

7.51

Hence, the coefficients , , and in equation (7.41) can be written as

7.52

In this case, . This implies that equation (7.40) turns into

7.53

Hence, equation (7.42) turns into

7.54

The expression of is the same as that of equation (7.43) with

7.55

The solution of the integrals required is given next. If we define , then the first and the second integrals are with the solution given as

7.56a

7.56b

7.57a

7.57b

7.57c

where the definitions used are

7.58

It is clear that the analytic solutions are not trivial to implement. However, it was found that they are much faster for closely located conductors. Also, the singularity for self-terms is automatically taken care of. The above equation is best used for very close cells while approximate solutions are more efficient for cells which are further apart.

Problems

1. 7.1 Conversion of coordinates

   Coordinate conversion is required for nonorthogonal, global coordinates to a quadrilateral element shown in Fig. 7.3. Show that points on the quadrilateral element can be converted into a point in the local by the formulation in Section 7.1 to a point on the surfaces of the quadrilateral shape. We note that the quadrilateral surface is bounded by the cornerpoints points 0 to 3. Show that the points (a, b) in the −1, +1 range correspond to global coordinate points (x, y, z) by using equation (7.3).

2. 7.2 Continuity equation

   Explain the function of the continuity equation in relation to the equivalent circuit in Fig. 7.7. Show that equation (7.27) is based on the continuity equation for the nonorthogonal geometry shown.

3. 7.3 Resistance for nonorthogonal geometries

   Prove equation (7.14) for the resistance of the nonorthogonal geometries. Also, we don't consider possible resistive couplings due to the nonorthogonal overlap of resistive cells. Find a formula for the resistive coupling between overlapping cells, which is an extension of (7.14). An example for resistive coupling in Fig. 7.3 for two overlapping inductance half cells which are connected between nodes 0 and 2 and the other one is connected between nodes 0 and 1. Of course the quadrilateral is not rectangular.

4. 7.4 PEEC inductance circuit model for coupled current strips

   This problem is very similar to the first problem in Chapter 6. However, the conductor shape is trapezoidal rather than rectangular. The thickness and the corner point is and the width for the trapezoidal strip in Fig. 7.15. The same way as in the first problem in Chapter 6, split the strip in the middle into two pieces that are connected at the ends. These two half-cell pieces are coupled to each other. Build an inductance–resistance PEEC model for the strip two partial. Make an equivalent circuit for the problem. Is the model an open-loop model?

   

References

1. 1. P. K. Wolff and A. E. Ruehli. Inductance computations for complex three dimensional geometries. In Proceedings of the IEEE International Symposium on Circuits and Systems, pp. 16–19, 1981.
2. 2. R. F. Milsom, K. J. Scott, G. Clark, J. C. McEntegart, S. Ahmed, and F. N. Soper. FACET – a CAE system for RF analogue simulation including layout. In Proceedings of the Design Automation Conference, Volume 26, pp. 622–625, 1989.
3. 3. R.-B. Wu, C.-N. Kuo, and K. K. Chang. Inductance and resistance computations for three-dimensional multiconductor interconnection structures. IEEE Transactions on Microwave Theory and Techniques, MTT-40(2):263–270, February 1992.
4. 4. M. Kamon, M. J. Tsuk, and J. White. FastHenry: a multipole-accelerated 3-d inductance extraction program. In Proceedings of the Design Automation Conference, pp. 678–683, June 1993.
5. 5. Y. Wang, V. Jandjayla, and C.-J. R. Shi. Coupled electromagnetic-circuit simulation of arbitrary-shaped conducting structures. In Digest of Electrical Performance of Electronic Packaging, Volume 10, Boston, MA, pp. 233–236, October 2001.
6. 6. A. Rong and A. C. Cangellaris. Generalized PEEC models for three-dimensional interconnect structures and integrated passives of arbitrary shapes. In Digest of Electrical Performance of Electronic Packaging, Volume 10, Boston, MA, pp. 225–228, October 2001.
7. 7. M. Tröscher and H. Katzier. Efficient PEEC modeling of multi-layer boards and multi-chip modules. In Proceedings International Zurich Symposium on EMC, Volume 14, Zürich, Switzerland, pp. 269–273, February 2001.
8. 8. A. E. Ruehli, G. Antonini, and A. Orlandi. Extension of the partial element equivalent circuit method to non-rectangular geometries. In Proceedings of the IEEE International Symposium on Electromagnetic Compatibility, Seattle, WA, pp. 728–733, August 1999.
9. 9. G. Antonini, A. Ruehli, and J. Esch. Non orthogonal PEEC formulation for time and frequency domain modeling. In Proceedings of the IEEE International Symposium on Electromagnetic Compatibility, Minneapolis, MN, August 2002.
10. 10. A. E. Ruehli, G. Antonini, J. Esch, J. Ekman, A. Mayo, and A. Orlandi. Non-orthogonal PEEC formulation for time and frequency domain EM and circuit modeling. In Proceedings of the IEEE International Symposium on Electromagnetic Compatibility, Volume 45, pp. 167–176, May 2003.
11. 11. B. M. Kolundzija and B. D. Popovic. Entire-domain Galerkin method for analysis of metallic antennas and scatterers. IEE Proceedings H Microwaves, Antennas and Propagation, 140(1):1–10, January 1993.
12. 12. H. Singer, H.-D. Brüns, and G. Bürger. State of the art in the moment method. In Proceedings of the IEEE International Symposium on Electromagnetic Compatibility, Santa Clara, CA, pp. 122–227, August 1996.
13. 13. G. Antonini, S. Cristina, and A. Orlandi. PEEC modeling of high voltage tower under direct and nearby lightning strike. In Proceedings of the 10th International Symposium on High Voltage Engineering ISH, Volume 10, Montreal, CA, August 1997.
14. 14. K.-B. Wu, G.-H. Shiue, W.-D. Guo, C.-M. Lin, and R.-B. Wu. Delaunay-Voronoi modeling of power-ground planes with source port corrections. IEEE Transactions on Advanced Packaging, 31(2):303–310, May 2008.
15. 15. H. Shi, J. Fan, and J. Drewniak. Modeling multilayered PCB power-bus designs using an MPIE based circuit extraction technique. In Proceedings of the IEEE International Symposium on Electromagnetic Compatibility, Denver, CO, pp. 647–651, August 1998.
16. 16. J. F. Fan, H. Shi, A. Orlandi, J. L. Knighten, and J. L. Drewniak. Modeling DC power-bus structures with vertical discontinuities using a circuit extraction approach based on a mixed-potential integral equation formulation. IEEE Transactions on Advanced Packaging, 24:143–157, May 2001.
17. 17. A. E. Ruehli, G. Papadopoulos, E. Michielssen, A. Cangellaris, and K. Aygun. Transient analysis for printed circuit board problem using two different solvers. In Proceedings of the IEEE International Symposium on Electromagnetic Compatibility, Montreal, CA, pp. 1327–1332, August 2001.
18. 18. B. Archambeault and A. E. Ruehli. Analysis of power/ground-plane EMI decoupling performance using the partial-element equivalent circuit technique. IEEE Transactions on Electromagnetic Compatibility, 43(4):437–445, November 2001.
19. 19. C.-T. Tai. Generalized Vector and Dyadic Analysis. IEEE Press, New York, 1992.
20. 20. S. Ramo, J. R. Whinnery, and T. Van Duzer. Fields and Waves in Communication Electronics. John Wiley and Sons, Inc., New York, 1994.
21. 21. C. Ho, A. Ruehli, and P. Brennan. The modified nodal approach to network analysis. IEEE Transactions on Circuits and Systems, 22(6):504–509, June 1975.
22. 22. A. E. Ruehli. Equivalent circuit models for three dimensional multiconductor systems. IEEE Transactions on Microwave Theory and Techniques, MTT-22(3):216–221, March 1974.
23. 23. G. Antonini, A. Orlandi, and A. Ruehli. Analytical integration of quasi-static potential integrals on non-orthogonal coplanar quadrilaterals for the PEEC method. IEEE Transactions on Electromagnetic Compatibility, 44(2):399–403, May 2002.
24. 24. P. Arcioni, M. Bressan, and L. Perregrini. On the evaluation of the double surface integrals arising in the application of the boundary integral method to 3-d problems. IEEE Transactions on Microwave Theory and Techniques, 45(3):436–439, March 1997.
25. 25. W. Gander, M. Gander, and M. Kwok. Scientific Computing, An introduction using Maple and MATLAB, Springer-Verlag, Berlin and New York, 2014.