Chapter 10
PEEC Models for Dielectrics
Many practical problems include dielectric insulating materials, substrates, dielectric coatings, and other applications of dielectric materials. Hence, it is important to also include dielectrics in partial element equivalent circuit (PEEC) models. A fundamental, physics-based representation of the dielectric issues is presented in [1]. We concentrate on inclusion of several different dielectric circuit-oriented models in PEEC to cover a wide range of applications.
Specifically, three different issues are considered in this chapter. First, we treat the electrical description of dielectric materials in the time and frequency domains. Second, we consider different approaches for the description of the properties of dielectrics such that they can be included in the solution. Third, we present approaches for the inclusion of dielectrics in a PEEC model.
10.1 Electrical Models for Dielectric Materials
10.1.1 Frequency and Time Domain Models for Dielectric Materials
Dielectrics can be lossless or lossy, and the dielectric constant 
can be frequency or time dependent or independent. Hence, models must be available and suitable for many different cases. Today, the inclusion of frequency or time dependence in dielectrics is important as the ever-increasing frequencies present challenges.
Clearly, the most simple dielectric model in PEEC is if a uniform relative dielectric constant 
can be used. Hence, the assumption is that the entire dielectric space consists of the same material. A fair number of problems can be represented with such a model, which is straightforward to implement. We replace 
by the new dielectric constant 
for all partial potential coefficients in the frequency domain. For the lossless dielectric case, the same approach can be applied in the time domain. This approach is considered in more detail in Section 10.4.1.
Fortunately, most of the dielectric models can be represented with an equivalent circuit description such that they can naturally fit into the PEEC circuit environment.
In the frequency domain, a general formulation for the relative permittivity of lossy material is specified in the form
where 
is the real part of the dielectric constant, 
represents the loss part, and 
is the angular frequency.
Perhaps another more clear notation used for (10.1) is
where the notation used for the real part is 
and for the imaginary part 
, Ref. [2]. The loss tangent is defined by 
. For convenience, we use both notations in this chapter.
For conventional dielectrics, a slow decrease with frequency in the important region is observed for 
for realistic lossy dielectrics. The loss tangent is less predictable in its variation with frequency. If it is not zero for 
, then the material also has a dc resistance. Furthermore, we want to point out that a loss tangent 
which is constant with frequency is inconsistent with the behavior of 
as discussed in the following section. It is important to recognize that we do not have complete data over the entire frequency range 
from physical measurement. Unfortunately, this results in problems finding dielectric models for the new, faster technologies and denser layout IC designs, for example, Refs [3, 4].
A question that is beyond the scope of this book is the availability of accurate broadband data for the complex permittivity 
. However, very accurate broadband data for dielectrics above the 100 GHz range is harder to obtain. Very often, a loss tangent is specified for material properties. As is evident from (10.2)
From (10.10), it is also evident that the loss tangent 
is an odd function of frequency, as is clearly pointed out in Ref. [5].Importantly, Hilbert consistent, causal models of dispersive and lossy dielectrics cannot have a constant relative permittivity 
. Hilbert consistency or the equivalent Kramers–Krönig relation is considered in Section 10.1.3.
10.1.2 Models for Lossy Dielectric Materials
The models for dielectrics must be suitable to represent different material behavior such that they can be embedded in a PEEC solution as efficiently as possible. As was pointed out in, for example, Refs [6, 7], significant mismatches have been observed for model with lossy dielectrics between measurements and results for 2D quasistatic (QS) models used for 3D interconnect problems. This is especially true if they are used with transmission line tranverse electromagnetic mode (TEM) mode type models. A better approximation is required for quasistatic (QS)PEEC models with losses included. The full-wave (FW) PEEC models are even more challenging from an implementation point of view.
10.1.3 Permittivity Properties of Dielectrics
The properties of dielectrics are mostly given in the frequency domain rather than the time domain. In general, we need to know both 
and 
to properly use the material. The interesting aspect is that once either the real or imaginary part of the dielectric model is known for the entire frequency range 
, then the other part is uniquely determined by the so-called Hilbert transform. Experimentally, we lack the complete knowledge of the data for the entire frequency range. From a theoretical point of view, if the material satisfies the Hilbert relations between the real and the imaginary parts [8], then we say that it is Hilbert consistent, which is clearly an important feature for obtaining passive models considered in Chapter 13.
We use the Hilbert transform between the real and imaginary parts 
and 
. For dielectrics, it is also called the Kramers–Krönig relations [10] that are
where 
denotes the principal value. Fortunately, this implies that the singular points are such that for the numerical integration of the integrals, we can ignore the behavior in the immediate small neighborhoods on both sides near the singularities. An equivalent form that is easier to implement is given by
which uses positive frequencies only.
Hilbert consistency between the real and imaginary parts of the relative dielectric constant is essential for the construction of passive models, for example, Ref. [5, 8].
10.1.4 Electrical Permittivity Model for Time Domain
We start from (3.2b) in Chapter 3, which is 
. We also need to define the electric susceptibility 
, which is given as
With this, the susceptibility can be written as
using the usual time domain convolution. To obtain 
, we have to use the inverse Fourier transform of the frequency dependent dielectric constant such that we obtain
Of course, this corresponds to the time-to-frequency forward Fourier transform
If the quantities 
and 
are positive real functions [11, 12], we have for real frequencies 
that
where 
is an even function. Causality of the electromagnetic (EM) solution is in question if the relationships (10.10) are violated [5, 8].
10.1.5 Causal Models for Dispersive and Lossy Dielectrics
We pointed out in Section 10.1.3 that Hilbert consistent models are required to construct valid EM solutions for lossy dielectrics. Theoretically, we assume that all the relevant quantities are known for the entire frequency range 
. However, we are lucky if the electrical permittivity 
is known for a sufficient number of frequency decades. Furthermore, it is well known that many EM-solver techniques do not provide a dc solution.
A class of circuit-oriented models is represented by a ratio of polynomials in 
where all coefficients are real. A general band-limited susceptibility function 
is of the form
In these polynomials, the order of the denominator must be larger than the numerator such that the model leads to 
at the limit 
. Thus, the general form of the electrical permittivity 
is
where 
describes the permittivity at 
.
The most common and simple dispersive dielectric model is the single-pole Debye model:
where 
is the relaxation constant. A Lorentzian model is defined as
where 
is the relaxation constant and 
is the resonance angular frequency. The Debye model has its main applications in the subterahertz range, whereas the Lorentz model yields a better approximation for higher resonance models. We also observe that a model with a single real or complex pole pair is a very narrow-band model valid only for a limited frequency range.
In general, broadband models are obtained by addition of several models of the form of (10.13) or (10.14). However, we have to point out the computational cost which each additional term implies. These models are of the general form
where parameters 
, 
, 
, 
and 
are all positive and satisfy the following conditions:
where 
and 
represent the permittivity at dc and at infinite frequency. In these equations, 
represents the number of Debye terms according to (10.13) and 
are the number of Lorentz terms according to (10.14).
Fortunately, a loss model can be designed for high-speed electrical interconnect applications using typical dielectric materials such as FR-4. As an example, a result is given in Fig. 10.1, where we show the magnitude of permittivity and loss tangent for DriClad. The results, which are valid for about four decades, are obtained with a fourth-order Debye model, where 
, 
, and the other parameters chosen as shown in Section 10.3. The Debye model parameters are carefully chosen terms (
) to keep the computational cost at a minimum.
Figure 10.1 Fourth-order Debye model for DriClad. (a) Magnitude of permittivity. (b) Loss tangent.
For completeness, we also include two additional models. For example, for polymer and composite materials, the Cole–Cole dispersion law is also widely used [13, 14], which is
This model can also be approximated by fitting a sum of third and fourth terms in (10.15). We should note that (10.17) is a special case of the more general dispersion law described by the Havriliak–Negami function [15, 16]
In general, these formulas can also be used in multiterm form (10.15).
10.2 Circuit Oriented Models for Dispersive Dielectrics
Circuit models for dielectrics are of importance for several reasons. We considered techniques in Chapter 2 on the inclusion of frequency-dependent circuits in the PEEC–modified nodal analysis (MNA) time solution. The best choice for the implementation of the dispersive model depends on the complexity of the model. The recursive convolution approach in Section 2.10.2 is preferable for the inclusion of very complicated circuit models with a large number of circuit elements and internal nodes.
An equivalent circuit-based approach is very suitable for a PEEC model with a smaller number of nodes since it allows the use of the conventional solver techniques presented in Chapter 2. Another important factor is always for a model to be suitable for both the time and the frequency domain. This simplifies the solution in both domains.
In the following sections, equivalent circuits are presented for the Debye model, the Lorentz model, and other general combined models.
10.2.1 Simple Debye Medium Circuit Model for Dielectric Block
We first consider the one-pole Debye model (10.13) for lossy dielectrics. The equivalent circuit is used from the dielectric PEEC model in Section 10.4.5. This one-pole model is the most simple for dielectrics with loss resulting in the least number of unknowns or compute time. However, a single-pole model can only accommodate a limited frequency range. Figure 10.2 shows the geometry for the dielectric bar cell for which we apply the model. We assume that the crosshatched areas are the contact surfaces.
Figure 10.2 Rectangular block of dielectric material.
The admittance of the block of dielectric material in Fig. 10.2 for a Debye model is
where the model parameters to be specified are 
, 
and 
.
It is easy to identify the equivalent circuit parameters. The capacitive admittance can be rewritten as
where the capacitance at 
, 
is given by
The RC series parameters are
and
The corresponding equivalent circuit is shown in Fig. 10.3.
Figure 10.3 Equivalent circuit for a one-pole Debye medium.
Again, this simple model can only represent a limited variation of the permittivity with frequency. The implementation of the circuit model in the MNA solution works equally well for both the frequency and the time domains since all the elements in the equivalent circuit are frequency independent.
10.2.2 Simple Capacitance Model for Lorentz Media
The Lorentz media equations add somewhat more flexibility over the Debye model, which is necessary for some materials since it involves possibly complex pole behavior. Applying the same reasoning as in the Debye model case, the equivalent circuit for the model is given in Fig. 10.4.
Figure 10.4 Complex pole equivalent circuit for a Lorentz medium.
The admittance for the model branch is given by
where the shape of the dielectric block is the same as for the Debye model in Fig. 10.2. The first term in (10.24) is again the admittance of the excess capacitance at infinite frequency and the second one is treated as an admittance 
for the series connection in the equivalent circuit in Fig. 10.4 such that we have
where 
. It is a small task in circuit analysis to find the values of the circuit elements. Some simple manipulations allow us to synthesize 
as a series 
equivalent circuit with the following values of circuit parameters:
in the equivalent circuit in Fig. 10.4.
We notice that at very high frequencies, the admittance of the capacitance that dominates is 
. For very low frequencies, the admittance of the circuit is 
.
We can verify that the equivalent circuit is also consistent for the nondispersive case. This can be obtained for the low-frequency range assuming that 
. Then in Fig. 10.4, the series 
circuit reduces to the capacitor 
. Thisshows that the global circuit is equivalent to the static excess capacitance 
.
To enhance the accuracy of a model, we have to add the losses to a model by including a loss with the appropriate 
and a 
. We note that a frequency-independent loss factor is not physically consistent since it does not represent the high frequencies correctly [5].
10.3 Multi-Pole Debye Model
The models presented in the previous two sections allow only a limited frequency variation because of the small number of poles used. However, the frequency dependence can be improved by adding more sections to the model. The Debye model with multiple poles is widely used, and the complexity is limited only by the need to keep the number of poles as small as possible. Additional poles added to a model cover a broader frequency range. Specifically, we consider a multipole Debye model, where potentially only one pole is used for each frequency decade to maintain the computational efficiency.
It is possible to design a physical consistent Debye model starting from the limited set of data, 
, 
, and 
, where 
and 
now have the meaning of loss tangent and time constant of the first relaxation process. In the following, we refer to Ref. [17] where a methodology is presented to obtain analytically the Debye model parameters for substrates with a constant loss tangent over a specified bandwidth. Hence, a multipole Debye model leads to
where the number of poles is determined by 
.
Figure 10.5 shows the circuit representation of the Debye model where 
, determined by 
, impacts the constant highest frequency behavior of the dielectric.
Figure 10.5 
N-pole Debye dielectric equivalent circuit.
In order to obtain a sufficiently smooth loss tangent over several decades, multiple 
branches have to be included. According to Ref. [17], the values of the circuit elements in 
branches in the equivalent network can be evaluated as
for 
; 
is a scale factor set to 1 for 
and to 0.9 for 
. The capacitances 
and 
must meet the low frequency condition
Actually, 
corresponds to 
and the knowledge of 
, 
, and the number of poles 
allow us to obtain 
that determines 
from
Once 
and 
are known, all the other parameters can be evaluated from the analogy between the Debye model (10.27) and the 
circuit
We should note that the multipole Debye circuit model is automatically Hilbert consistent.
We give an example for a multipole Debye model. The structure consists of a microstrip line over a dielectric layer with a ground plane underneath. The lossy dielectric layer is 1 mm thick and the zero thickness trace is 1 mm wide while the overall length of the structure is 10 cm.
We choose an FR-4 dielectric material in the example with a 
and 
, where 
in (10.27). Equation (10.28a) is used to determine the other time constants for the number of poles, which are 
. This results in the representation of the dielectric as
where 
and 
is again the time constant of the 
th relaxation process, respectively. The parameters used are summarized in Table 10.1.
Table 10.1 FR-4 Debye model parameters.
 |
 |
 (ns) |
|
| Pole 1 | 4.7 | 4.55 | 1.59 |
| Pole 2 | 4.55 | 4.40 | 0.159 |
| Pole 3 | 4.40 | 4.25 | 0.0159 |
| Pole 4 | 4.25 | 4.10 | 0.00159 |
Figure 10.6 FR-4 loss tangent representation for an increasing number of poles (example in Section 10.5.2).
Figure 10.7 FR-4 permittivity representation for an increasing number of poles.
Figures 10.6 and 10.7 show the loss tangent and the magnitude of electrical permittivity where the number of poles is increased from 1 to 4. This illustrates how the number of poles to the model increases the frequency range for which the model is valid. The overall PEEC model mesh included 924 volume cells for the volume filament (VFI) skin-effect inductance model and 760 zero thickness surface cells, resulting in 924 currents and 168 nodes since some of the capacitive cells are joined at the nodes in this example.
10.3.1 Combined Debye and Lorentz Dielectric Model
This model is added mostly for generality since its complexity contributes to very long compute times. Of course, the models are very general in representing the behavior of different materials by the sum of Debye and Lorentz terms. We assume that 
Debye and 
Lorentz terms are combined in the form of (10.15)
where 
is the permittivity at infinite frequency, 
and 
are the static dielectric constants for the 
th Debye and Lorentz medium, 
is the resonance frequency of the 
th Lorentz medium. The loss constant of the 
th Debye term is 
. The admittance corresponding to the capacitance is
which is given by the synthesized circuit shown in Fig. 10.8. The techniques presented in these sections are applied in the rest of this chapter.
Figure 10.8 Equivalent circuit for a general dispersive dielectric.
10.4 Including Dielectric Models in PEEC Solutions
Dielectric models have so far been presented independently of how we include them in a PEEC model. Different approaches will be presented below which show applications of the dielectric models presented so far in this chapter. The model we use may be problem specific and not general. Mainly, the compute time for general techniques could be excessive in some cases. For example, only a limited number of approaches apply to lossy full-wave (FW)PEEC models.
It is important that not all dielectric models result in an increase in the size of the PEEC circuit model. For example, the technique in Section 10.4.2 impacts the Green's function rather than the circuit topology of the PEEC model. This exemplifies the fact that a combination of circuits as well as EM techniques can be mixed for different solution methods.
10.4.1 Models for Uniform, Lossless Dielectrics
In the most simple situation, we can use a model where the entire problem is embedded in a uniform dielectric material, which, theoretically, extends to infinity in all directions. The relative dielectric constant 
is replaced by 
for all the partial potential coefficients. This uniformly results in a reduces velocity 
everywhere 
, where 
is the speed of light in air.
This can result in very effective solutions for many problems. While the implementation in PEEC is simple, we notice that the meshing also needs to be made more dense to achieve the same accuracy. The mesh size has to be reduced by 
. This can result in a significant increase in compute time for very high values of 
. Also, the inclusion of lossy dielectric regions with 
can be used to make the problem lossy.
Figure 10.9 Two infinite dielectric layers geometry for images.
10.4.2 Green's Functions for Dielectric Layers Based on the Image Theory
Dielectric layers can be taken into account in a different way. First, we show that they can be included directly in the Green's function by a combination of free-space type Green's functions. The capacitance and inductance models are de-coupled, and the Green's functions are not classified by the direction of the current, etc., as is the case for the ones considered in Chapter 3 and Section 3.4.
The details of the solution are determined by the location of the source and observation points in the layer structure. For this reason, we label the Green's functions according to the layer region where the observation point and the field points are located. For example, for the Green's function 
the observation point is in region 1 while the source point is in region 2.
The method of images we use has a long history, e.g., [18, 19]. The image planes are theoretically infinite in size since the boundary conditions are matched between the entire planar layers.
We start with the two infinite dielectric half-spaces where the dielectric half-space above the boundary is filled with a dielectric constant of 
while the dielectric constant below the interface is filled with 
as shown in Fig. 10.9. We use the notation that 
for layer 
. For clarity, we only show a finite section of the infinite dielectric layer in Fig. 10.9 and all the subsequent figures for layered Green's functions. They extend to infinity in the 
and 
direction.
The interface between two dielectrics is in the 
plane and it is placed at a distance 
from the 
plane. We are interested in computing the potential at 
which may be located in one of the two dielectric regions. For the Green's function, we assume that a unit charge 
is placed at 
which can be located anywhere.
For the case when both observation point 
and the source point 
are located in the same dielectric region, the observation point sees two effects. One is the direct field contribution from the source direction through a distance vector 
and another one is the reflected contribution by the source. The reflection happens at the interface and its equivalence consists of a weighted image source. The total contribution of these two is added up for the Green's function 
.
If the observation point is in region 1 and the source point is in region 2, then the situation is different. A new weighted source has to be computed to find the Green's function 
. Obviously, there are two other cases to be considered when the observation point is located in region 2 instead. Fortunately, the above results can be used where the corresponding Green's functions are 
and 
, respectively.
In all cases, the solutions must satisfy the boundary conditions at the interface(s). One of the required boundary conditions is that the tangential electric fields are matched (3.14a)
on the two sides of the interface where 
is the tangential unit vector shown in Fig. 10.9. Since this boundary condition has to be satisfied at any point on the interface, we can put a tangential vector of unit length 
in any direction on the plane. For the unit length to be satisfied, we require that 
. Without loss of generality, we place the tangential vector at the origin in Fig. 10.9.
The second boundary condition which has to be met is the continuity of the normal electric displacement flux density for 
in (3.14c)
where 
is the unit normal vector on the dielectric interface and points into region 1 as shown in Fig. 10.9.
10.4.3 Green's Function for One Dielectric Interface
All the preliminaries for computing the Green's functions have been covered in the last section. Assume the observation point 
as well as the source point 
are in region 1. The contribution from the source charge 
located at 
is
Figure 10.10 Solution for region above the dielectric interface.
Based on the image theory we introduced at the beginning of this section, we can set up a proposed solution using one image source 
and then match the boundary conditions at the interface. Figure 10.10 shows the image solution valid for the region 1 case where both source and field positions are above the dielectric interface. If the image source is properly constructed, the electric field can be finally computed from the following equation
It is noted that the source charge 
and the image charge 
are the same distance to the other side of the common interface.
If the observation field position is in region 2 while the source 
is still 
in region 1, we use an image source 
located at 
that is working in a homogeneous medium with the same permittivity 
as region 2. The situation is shown in Fig. 10.11, where the electric field is
where 
is also unknown and the entire space is filled with 
. The two unknown charges 
and 
have to be found by matching the boundary conditions (10.35) and (10.36).
Figure 10.11 Solution for region below the dielectric interface.
To match the tangential components starting with (10.38), the dot product between with 
results in
Also for (10.39), we obtain
Equating (10.40) to (10.41), we obtain one of the equations for the determination of the charges
For the electric displacement 
normal boundary condition, we apply 
to (10.38) and (10.39), which results in the displacement flux density on the interface but in region 1 
:
Similarly, the normal dot product of the field on the interface and in region 2 is
For the evaluation of (10.37), matching (10.44) and (10.45) on the boundary 
, we get
Since 
is the original known charge, from the (10.42) and (10.45), we can solve 
and 
to be
where
Using 
and 
, we can revise the homogeneous Green's function to adapt the effects of the two dielectrics. As we considered before, there are four Green's functions that can be divided into two cases: two for the source charge point are in the upper layer Fig. 10.10 and two for the source point in the lower region.
The Green's function whose source and observation points are both in region 1 is found from (10.38) and the coefficient 
as
where we define to simplify 
.
Next, the Green's function whose observation point is in region 1 and the source charge is in region 2 is
The third case is for the observation point in region 2 and the source point in region 1. The result is
The last case is given when both the observation and the source point are region 2 with a dielectric constant 
Working out the proper images for the three dielectric layers considered in the next section is quite challenging. However, we can use the two layer results to significantly simplify the process since meeting local boundary conditions is the same for all cases of interest. We summarize the four Green's function in Fig. 10.12 where we show the location of the image as well as the reflection needed for the next section.
Figure 10.12 Reflection and image for the four Green's functions.
10.4.4 Three Dielectric Layers Green's Functions
Another class of problems which can be solved with the image method consists of three dielectric layers as shown in Fig. 10.13. Even for the more complicated problems, we can take advantage of what we did learn about the two layer dielectric problems. For the three dielectric layer problems, the observation point 
as well as the source point 
can be located in each of the three layer. This results in nine Green's functions for all the situations. However, fortunately only five Green's functions are needed to cover the fundamentally different functions. The rest of the equations can be obtained from the formulas in this section by a simple exchange of variables.
Figure 10.13 Example geometry for three dielectric layers.
For the three layer case considered, we have two reflection coefficients, 
for the upper dielectric interfaces and 
for the lower case. By applying (10.47) to the three layer situation in Fig. 10.13 we obtain
It is noticed from the above example in Fig. 10.12, that in general the regions where the observation point is located does not contain any image charges.
The locations of images are always equidistant from the interface. The strength of the images requires some thought in that the reflections must be considered carefully. Because there are multi-reflections due to the existence of two parallel dielectric boundaries, the coefficients 
in (10.52) have to be determined by multiple applications of the 
's in (10.53). A summary of diagrams in Fig. 10.12 is very helpful for the determination of the strength as well as the location of the images.
Figure 10.14 Images for 
where observation and source points are in layer 1.
We start with 
where both the source and the observation points are located in region 1 shown in Fig. 10.14.
Each of the situations lead to as new formulation. Also, 
can be derived from 
by a change of variables.
For the second Green's function, the source is still located in layer 1 while the observation point is in the middle layer 2, as shown in Fig. 10.15. By a change of variables we can construct 
from this result since the observation point is staying in layer 2.
Figure 10.15 Images for 
where the source point is in region 1 and the observation point is in region 2.
The third Green's function for which the source is in layer 1 is 
. The observation point is moved to layer or region 3, as shown in Fig. 10.16. We should note that by a change of variables in the solution can also be used to find the result for 
. Hence, both the source point and observation points are in the outside layers.
Figure 10.16 Images for where the source point is in region 1 and the observation point is in region 3.
For the case where the source point is in layer 2 and the observation point is in Layer 1 which is 
is treated next. We should observe that this solution can also used to obtain 
since the observation point is just in the other outer layer while the source point is in the same layer.
We give the reflection diagrams for 
in Fig. 10.17. The resultant Green's function is given in (10.57).
Figure 10.17 Images for 
where the source point is in region 2 and the observation point is in region 1.
Figure 10.18 Images for 
where the observation and source points are in region 2.
Finally, the Green's function for the case where both the source and observation point are in layer 2 is 
. In this case, images occur on both sides. The refections are shown in Fig. 10.18.
This includes the images which are needed to construct all cases required. Note that we also included the permitivtiy needed for each Green's function for clarity.
10.4.5 Dielectric Model Based on the Volume Equivalence Theorem
The technique presented in this section is based on the volume equivalence theorem in Section 3.5.1. The theorem allows the replacement of a finite dielectric body by charges and currents. The volume PEEC finite dielectric bodies was originally added to the classical PEEC conductor model in Refs [25, 21]. The model was extended to nonorthogonal-shaped bodies [22]. Surface PEEC models have also been added to the classical PEEC volume approach [23, 24], which includes finite dielectric bodies. This different approach is given in Section 11.4.2.
The volume model considered in this section transforms the dielectric materials to bound charges located in a uniform free space with a dielectric constant 
. Hence, this approach results in a very convenient model. Importantly, the technique can be used for both quasistatic (QS)PEEC models and full-wave (FW)PEEC models. Also, lossy and dispersive dielectrics are included in the model in Section 10.4.7.
Figure 10.19 Dielectric block between two zero thickness metal plates.
We start the derivation of the volume equivalence model with a simple problem consisting of a single dielectric block between two zero thickness conducting sheets, which is shown in Fig. 10.19.
As always, we consider a problem geometry, which may be part of a larger one, with other conductors or dielectrics. Here, we take a finite dielectric part only since the PEEC formulation for conductors is treated carefully in Chapter 6. This is permissible if we remember to take the couplings into account between all the different parts of the overall problem.
So far, we have dealt with the free charge density 
on conductors. To represent the dielectrics using the volume equivalence theorem given in Section 3.5.1, we use bound charge density 
that describes the dielectric charge where 
is handled separately from the conducting currents that are due to free charge 
. Maxwell's equation (3.1d) defines the relationship between the displacement flux density and the charge densities as
where 
is the free charge and 
is the bound charge.
We purposely chose an example in Fig. 10.19 where the side surfaces have a bound charge only, since the surfaces are dielectric–air interfaces. The top and bottom surfaces have dielectric bounded polarization charge densities 
as well as free charge densities 
due to the conductors.
The volume equivalence formulation is derived by adding and subtracting the displacement current 
in the free space through the Ampere's law for 
in Section 3.1.1 such that the formulation results
in the time domain. Of course, the formulation is the same if we replace the time derivative 
with the Laplace variable 
for a frequency domain solution. Thus, the total current in (10.59) takes into account both the conduction electric current related to the conductivity of the medium and the polarization current due to the dielectrics
Hence, considering that the last term is related to displacement current density, which is modeled by time variation of charges residing only on the surface of the objects, the total current within the dielectric is
which suggests a parallel RC circuit modeling both conductive and polarization current densities. From (10.60), we can define an equivalent dielectric current density 
as
We can include this term in the electric field integral equation in the form
This leads to the electric field equation for points in the dielectric region
corresponding to the conventional EFIE for conductors (3.25).
10.4.6 Discretization of Dielectrics
The next step is again the discretization of the integral equation and to construct an equivalent circuit for the equation. Fortunately, we already have discretized two out of the three right-hand-side terms in (10.64). For this reason, we are not repeating the parts that are given in Sections 6.1, 6.2 and 6.3.3. We need to construct the PEEC model for the first term, which is (10.63).
The same averaging technique that is used for the resistance (6.7) is used for this term. As an example, we pick a 
-directed cell in Fig. 10.19 for the derivation. Of course, all four vertical divisions are quarter cells. Then, the integration will be for the left-front cell
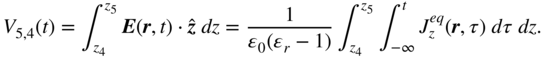
Using conventional current density averaging, we get
With the constant approximation in the 
-direction, this simplifies to
We note that the first part can be interpreted as the inverse of a parallel plate capacitance of the form 
or
However, we notice that the difference in the capacitance is proportional to 
. We recognize that this capacitance is in excess of the free space values. For this reason, it is called excess capacitance [21, 25].
We further observe that for a capacitor, the current and the voltage can be written as
It is clear from (10.70) that the model for the new term in (10.61) is interpreted as the equivalent circuit model in Fig. 10.20.
Figure 10.20 One section example of equivalent circuit for dielectric.
Some observations help to understand this important model.
- The excess capacitance
takes the dielectric constant above air 
into account. - A parallel resistance could be used to include a model for losses due to finite conductivity of the dielectric material. This would include dielectrics with a
resistance. - Surprisingly, a partial inductance
has to be computed for the dielectric cell. Also, all the partial inductances in a PEEC model are coupled including the dielectric ones. - Capacitive cells are only placed on surfaces with conductor–dielectric interfaces. Interfaces with dielectric cells only do not connect to the free-charge model.
We take a specific example to illustrate the last point. For example, node 5 in Fig. 10.19 includes several faces. The free side faces do not have free charge associated with them, whereas the top face does have a free charge associated with the conductor surface. However, bound charge or the excess capacitance 
is associated with all faces. This happens automatically when we compute 
for the model.
10.4.7 Dispersive Dielectrics Included in the Volume Equivalence Theorem Model
An important observation is that the models for dispersive dielectrics in Section 10.1 can directly be used in the volume equivalence theorem model. The implementation is simple since we can use any one of the dielectric models.
To give a specific example, we take the widely used multipole Debye model in (10.27) as part of the volume equivalence model. We consider the 
excess capacitance in Definition 10.1 and replace it with a model with the appropriate equivalent circuit.
The Debye model for the excess capacitance is given by
where 
, 
series branches are used in the circuit model. This model can be implemented in a solver with the equivalent circuit shown in Fig. 10.5.
10.4.8 Dispersive Dielectrics with Finite Electrical Conductivity
If a dispersive dielectric is characterized by a finite conductivity, then the corresponding equivalent circuit is obtained by placing a resistance representing the finite conductivity in parallel to the equivalent circuit for the dispersive behavior of the dielectric. An example of the equivalent circuit for a Debye medium with finite electrical conductivity is shown in Fig. 10.21. This model is based on the one-pole Debye model in Fig. 10.3 where as an example, a dc resistance 
is added to the equivalent circuit.
Figure 10.21 Equivalent circuit for a Debye medium with finite electrical conductivity.
10.4.9 Convolution Formulation for General Dispersive Media
The implementation of the frequency-dependent dielectrics is simple in the frequency domain since the dielectric model can directly be applied in (3.2b), 
. For the time domain, we use convolution as an alternative way to implement the dielectric model, which includes the susceptibility functions (10.11). The displacement vector (10.7) 
, for the linear dispersive medium is given by
in the time domain. Here, we simplified the notation by omitting the space variable dependence of the field quantities. Again, 
is the permittivity of free space and the electric susceptibility is given by 
.
A discrete time solution for the convolution at 
time steps 
, is
Fortunately, the recursive convolution algorithm from Section 2.10.2 can be used to speed up the computation. This has been done for a single-pole model [26] and also in PEEC framework [27].
As done in (2.80), the derivation can be based on a residue–pole model that directly fits with the Debye model for the volume dielectric model in Section 10.4.7, (10.71). Of course, it can also be used for a conventional Debye circuit model (10.27) if the number of elements is large.
which we can represent in the general form (2.83)
where 
are the usual residues and 
the poles.
The recursive convolution algorithm presented in Section 2.10.2 is
We write (10.76) recursively as
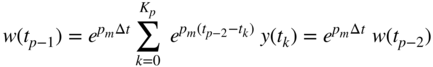
using (2.85) for the time step 
where 
is evident from (10.76) and by recursively computing 
. Using this approach, we can compute the solution as
by recursively updating. The last part in the convolution sum is evaluated by the recursive scheme [28]
where 
, which takes into account the past history and can be efficiently computed by a recursive scheme [28].
Figure 10.22 Transmission line example for lossy dielectrics.
Losses for the dielectric material are usually available in different forms. The use of table data as a function of frequency is a common approach. Alternatively, data is based on physics-based models such as the Lorentz or Debye models considered earlier. A fundamental requirement is that the real and imaginary parts of the data or model are Hilbert consistent. This implies that the requirements of the model for passivity are guaranteed, for example, Ref. [29].
10.5 Example for Impact of Dielectric Properties in the Time Domain
In this section, we want to illustrate the impact of the dielectric loss on the solution results. Additional examples for the application of the dielectric models are given in Ref. [27]. It is clear that at high frequencies both the dielectric losses and the skin-effect losses modeled in Chapter 9, are of importance. For this reason, we want to give examples that include both types of loss problems. We should specify that we assume that the conductors in all examples are copper. The conductivity of copper is specified in Appendix A.
Figure 10.23 Time domain output port voltage with Debye model with 
and different values of 
.
10.5.1 On-Chip Type Interconnect
We modeled the simple small interconnect connection over a ground plane shown in Fig. 10.22. The source resistance was 
and the termination was 
. The highest frequencies in the spectrum of the current impulse waveform is in the 50–100 GHz range. We considered the lossless dielectric case as well as a Debye model with different loss tangents. The mesh discretization was chosen using the 
rule such that 
corresponds to 200 GHz. This resulted in the unknowns of 948 currents or partial inductances and 156 node potentials for the PEEC model.
We applied a 1 V voltage source with a 20 ps rise time in this example. The dielectric has been modeled by a third-order Debye model with increasing values of 
for fixed values of 
and 
. The results of the analysis are shown in Fig. 10.23 for different dielectric loss tangent. We observe that the larger value of 
results in the reduction of the peak amplitude.
10.5.2 Microstrip Line with Dispersive, Lossy dielectric
In this section, we consider an example where the dielectric is represented by 
= 4 poles. The dielectric material was assumed to be FR-4 with 
, 
, 
. The dispersive, lossy behavior of the dielectric has been taken into account by means of a Debye model where
and where 
and 
are the value and the time constant for the 
th relaxation process, respectively. The parameters used are given in Table 10.2.
Table 10.2 Parameters for an FR-4 Debye model.
| Pole number |  |
 |
 |
| Pole 1 | 4.7 | 4.55 | 1.59 |
| Pole 2 | 4.55 | 4.40 | 0.159 |
| Pole 3 | 4.40 | 4.25 | 0.0159 |
| Pole 4 | 4.25 | 4.10 | 0.00159 |
Figure 10.24 FR-4 loss tangent for increasing number of poles (example in Section 10.5.2).
Figure 10.25 FR-4 permittivity for increasing number of poles (example in Section 10.5.2).
Figures 10.24 and 10.25 give the loss tangent and also the magnitude of electrical permittivity as a function of an increasing number of poles. Clearly, adding poles to the model increases the accuracy for a wider range of frequencies. From this, it is evident that for accurate wide-band frequency responses, multipole models are required.
Figure 10.26 Output port voltage (example in Section 10.5.2).
Figure 10.27 Magnitude spectrum of the output port voltage (example in Section 10.5.2).
A microstrip transmission line on a dielectric was modeled using this dispersive model. The trace with a zero thickness was 1 mm wide and the dielectric thickness was also 1 mm. The ground plane underneath was 1 cm wide and 10 cm long. The modeling resulted in 924 inductance volume cells and 760 capacitance surface cells. This lead to a PEEC model with 924 current unknowns and 168 potential nodes.
Both the source and the load resistances for the microstrip are 50 
. The input voltage source is a 2 V volt step with a rise time of 35 ps. The results for this example are shown in Fig. 10.26. The voltage given is for a perfect dielectric (solid line, Non Disp) and for Debye models with a different number of poles. In this example, the dielectric is taken into account using recursive convolution for this time domain response. The damping due to dispersion is clearly visible in the broadband loss model.
Figure 10.27 shows the voltage magnitude of the spectrum at the output obtained by using the two solvers, implementing dispersive and lossy dielectrics by means of equivalent circuits. A satisfactory agreement is reached in the frequency range 0–1 GHz.
Figure 10.28 Coplanar microstrip line (example in Section 10.5.3).
Figure 10.29 Near-end (a) and far-end (b) voltages for the coplanar lines. The solid line refers to the results obtained using the proposed methodology in the time domain (PEEC–TD–MNA). The dash–dot line refers to the results obtained using the finite integration technique (FIT) technique in the frequency domain via-inverse fast Fourier transform (IFFT) (FIT–FD–IFFT).
10.5.3 Coplanar Microstrip Line Example
A last example with dielectrics is based on two coupled lines on a lossy dielectric block with a size of 
with a thickness of 1 mm. The dielectric is again FR-4 and the loss is again represented with a fourth-order 
= 4 Debye model in a (QS)PEEC solution. As shown in Fig. 10.28, two 1 mm wide zero thickness wires are spaced by 3 mm centered on the dielectric. Both conductors are terminated with 50 
resistors, while one of them is driven by a 1 V source with a 30 ps rise and fall time where the pulse is 5 ns wide. The PEEC model is discretized with 1008 volume and 796 surface cells, which leads to 1008 partial inductance with currents and 176 nodes.
The response for the model for the coplanar microstrip transmission line shown in Fig. 10.29 was validated using an finite integration technique (FIT)-based computer simulation technology (CST) solver [30] in the frequency domain, which has been transformed to the time domain using the inverse fast Fourier transform (IFFT). The agreement can be observed to be very good.
Problems
- 10.1 Hilbert transform
Verify that you understand the Hilbert transform given in (10.4) and (10.5). Note that they should be satisfied for the real and imaginary parts of any complex impedance function. An important issue is how we take care of the singular behavior when
. Describe how you numerically treat the singularity in the Hilbert integrals. - 10.2 Debye model evaluation
Plot the magnitude of the permittivity and the loss tangent versus frequency for the fourth-order Debye model introduced in Section 10.1.5, (10.15). Do not use the Lorentzian terms in the model.
- 10.3 Lorentz medium
Derive an equivalent circuit for Lorentz medium using a complex pole model. (Hint: Complex pole models are discussed in Chapter 2.)
- 10.4 Static Green's function
Using Fig. 10.12 explain the contributions to the static Green's function in (10.53).
- 10.5 Asymptotic form of the static Green's function
Assume that a problem consists of air above a planar dielectric half space. Assume that the permittivity
is close to infinite. Derive the static Green's function asymptotically based on the results from (10.48)–(10.51).
References
- 1. P. G. Huray. The Foundations of Signal Integrity. John Wiley and Sons, Inc., New York, 2010.
- 2. C. A. Balanis. Advanced Engineering Electromagnetics. John Wiley and Sons, Inc., New York, 1989.
- 3. R. Achar and M. Nakhla. Simulation of high-speed interconnects. Proceedings of the IEEE, 89(5):693–728, May 2001.
- 4. E.-P. Li. Electrical Modeling and Design for 3D System Integration. John Wiley and Sons, Inc., New York, Hoboken, NJ, 2012.
- 5. K. M. C. Branch, J. Morsey, A. Cangellaris, and A. Ruehli. Physically consistent transmission line models for high-speed interconnects in lossy dielectrics. IEEE Transactions on Advanced Packaging, 25(2):129–135, May 2002.
- 6. M. J. Kobrinsky, S. Chakravarty, D. Jiao, M. Harmes, S. List, and M. Mazumder. Experimental validation of crosstalk simulations for on-chip interconnects at high frequencies using S-parameters. In Digest of Electrical Performance of Electronic Packaging, pp. 329–332, October 2003.
- 7. D. Jiao, C. Dai, S.-W. Lee, T. R. Arabi, and G. Taylor. Computational electromagnetics for high-frequency IC design. In Proceedings of IEEE Antennas and Propagation Society International Symposium, Volume 3, pp. 3317–3320, June 2004.
- 8. P. Triverio, S. Grivet-Talocia, M. S. Nakhla, F. G. Canavero, and R. Achar. Stability, causality, and passivity in electrical interconnect models. IEEE Transactions on Advanced Packaging, 30(4):795–808, November 2007.
- 9. E. C. Titchmarsh. Introduction to the Theory of Fourier Integrals. Clarendon Press, Oxford, 1967.
- 10. L. D. Landau and E. M. Lifshitz. Electrodynamics of Continuous Media. Addison Wesley Publishing Company, New York, London, Paris, 1960.
- 11. R. E. Diaz and N. G. Alexopoulos. An analytic continuation method for the analysis and design of dispersive materials. IEEE Transactions on Antennas and Propagation, 45(11):1602–1610, November 1997.
- 12. K. Inan and R. E. Diaz. Automatic analytic continuation method for the analysis and design of dispersive materials. IEEE Transactions on Antennas and Propagation, 59(4):1228–1236, April 2011.
- 13. K. S. Cole and R. H. Cole. Dispersion and absorption in dielectrics. Journal of Chemical Physics, 9(4):341–351, 1941.
- 14. D. W. Davidson and R. H. Cole. Dielectric relaxation in glycol, propylene glycol and n-propanol. Journal of Chemical Physics, 19(12):1484–1490, 1951.
- 15. S. Havriliak and S. Negami. A complex plane analysis of
dispersion in some polymer systems. Journal of Polymer Science, Part C, 14(1):99–117, 1966. - 16. E. Tuncer and S. M. Gubanski. On dielectric data analysis. Using the Monte Carlo method to obtain relaxation time distribution and comparing non-linear spectral function fits. IEEE Transactions on Dielectrics and Electrical Insulation, 8(3):310–320, June 2001.
- 17. A. E. Engin, W. Mathis, W. John, G. Sommer, and H. Reichl. Time domain modeling of lossy substrates with constant loss tangent. In 6th IEEE Workshop on Signal Propagation on Interconnects, Heidelberg, Germany, pp. 151–154, May 2004.
- 18. E. Weber. Electromagnetic Theory. Dover Publications, New York, 1965.
- 19. S. Ramo, J. R. Whinnery, and T. Van Duzer. Fields and Waves in Communication Electronics. John Wiley and Sons, Inc., New York, 1994.
- 20. L. J. Jiang, W. C. Chew, and Y. C. Pan. Capacitance Extraction in the Multilayer Medium Using DCIM and SMFMA. Journal of Electromagnetic Waves and Applications, 19(14):1851–1864, 2005.
- 21. H. Heeb and A. Ruehli. Three-dimensional interconnect analysis using partial element equivalent circuits. IEEE Transactions on Circuits and Systems, 39(11):974–982, November 1992.
- 22. A. E. Ruehli, G. Antonini, J. Esch, J. Ekman, A. Mayo, and A. Orlandi. Non-orthogonal PEEC formulation for time and frequency domain EM and circuit modeling. In Proceedings of the IEEE International Symposium on Electromagnetic Compatibility, Volume 45, pp. 167–176, May 2003.
- 23. A. Rong and A. C. Cangellaris. Generalized PEEC models for three-dimensional interconnect structures and integrated passives of arbitrary shapes. In Digest of Electrical Performance of Electronic Packaging, Volume 10, Boston, MA, pp. 225–228, October 2001.
- 24. D. Gope, A. Ruehli, and V. Jandhyala. Surface-based PEEC formulation for modeling conductors and dielectrics in time and frequency domain combined circuit electromagnetic simulation. In Digest of Electrical Performance of Electronic Packaging, Volume 13, Portland, OR, pp. 329–332, October 2004.
- 25. A. E. Ruehli and H. Heeb. Circuit models for three-dimensional geometries including dielectrics. IEEE Transactions on Microwave Theory and Techniques, 40(7):1507–1516, July 1992.
- 26. G. Antonini. PEEC modelling of Debye dispersive dielectrics. In Electrical Engineering and Electromagnetics (Eds C. A. Brebbia and D. Polyak), WIT Press, Southampton, pp. 126–133, 2003.
- 27. G. Antonini, A. E. Ruehli, and A. Haridass. Including dispersive dielectrics in PEEC models. In Digest of Electrical Performance of Electronic Packaging, Princeton, NJ, pp. 349–352, October 2003.
- 28. K. S. Kunz and R. J. Luebbers. The Finite Difference Time Domain Method for Electromagnetics. CRC Press, Boca Raton, FL, 1993.
- 29. T. R. Arabi, A. T. Murphy, T. K. Sarkar, R. F. Harrington, and A. R. Djordjevic. On the modeling of conductor and substrate losses in multiconductor, multidielectric transmission line systems. IEEE Transactions on Microwave Theory and Techniques, 39(7):1090–1097, July 1991.
- 30. Computer Simulation Technology, www.cst.com. CST Studio Suite, 2006B, 2007.