4.3 Polynomial Division; The Remainder Theorem and the Factor Theorem

  • Perform long division with polynomials and determine whether one polynomial is a factor of another.

  • Use synthetic division to divide a polynomial by x−cx−c.

  • Use the remainder theorem to find a function value f(c)f(c).

  • Use the factor theorem to determine whether x−cx−c is a factor of f(x)f(x).

In general, finding exact zeros of many polynomial functions is neither easy nor straightforward. In this section and the one that follows, we develop concepts that help us find exact zeros of certain polynomial functions with degree 3 or greater.

Consider the polynomial

h(x)=x3+2x2−5x−6=(x+3)(x+1)(x−2).
h(x)=x3+2x2−5x−6=(x+3)(x+1)(x−2).

The factors are

x+3, x+1, and x−2,
x+3, x+1, and x−2,

and the zeros are

−3,  −1, and 2.
−3,  −1, and 2.

When a polynomial is expressed in factored form, each factor determines a zero of the function. Thus if we know the factors of a polynomial, we can easily find the zeros. The “reverse” is also true: If we know the zeros of a polynomial function, we can find the factors of the polynomial.

Division and Factors

When we divide one polynomial by another, we obtain a quotient and a remainder. If the remainder is 0, then the divisor is a factor of the dividend.

Example 1

Divide to determine whether x+1x+1 and x−3x−3 are factors of

x3+2x2−5x−6.
x3+2x2−5x−6.

Solution

We divide x3+2x2−5x−6x3+2x2−5x−6 by x+1x+1.

Since the remainder is 0, we know that x+1x+1 is a factor of x3+2x2−x3+2x2− 5x−65x−6. In fact, we know that

x3+2x2−5x−6=(x+1)(x2+x−6).
x3+2x2−5x−6=(x+1)(x2+x−6).

We divide x3+2x2−5x−6x3+2x2−5x−6 by x−3x−3.

x2+5x+10x−3x3+2x2−5x−6x3−3x2¯5x2−5x5x2−15x¯10x−610x−30¯24← Remainder
x2+5x+10x−3x3+2x2−5x−6x3−3x2¯¯¯¯¯¯¯¯¯¯¯¯5x2−5x5x2−15x¯¯¯¯¯¯¯¯¯¯¯¯¯¯10x−610x−30¯¯¯¯¯¯¯¯¯¯¯¯¯24←−−−−−−−−−−− Remainder

Since the remainder, 24, is not 0, we know that x−3x−3 is not a factor of x3+2x2−5x−6x3+2x2−5x−6.

Now Try Exercise 3.

When we divide a polynomial P(x)P(x) by a divisor d(x)d(x), a polynomial Q(x)Q(x) is the quotient and a polynomial R(x)R(x) is the remainder. The quotient Q(x)Q(x) must have degree less than that of the dividend P(x)P(x). The remainder R(x)R(x) must either be 0 or have degree less than that of the divisor d(x)d(x).

As in arithmetic, to check a division, we multiply the quotient by the divisor and add the remainder, to see if we get the dividend. Thus these polynomials are related as follows:

For instance, if P(x)=x3+2x2−5x−6P(x)=x3+2x2−5x−6 and d(x)=x−3d(x)=x−3, as in Example 1, then Q(x)=x2+5x+10Q(x)=x2+5x+10 and R(x)=24R(x)=24, and

P(x)=d(x)⋅Q(x)+R(x)x3+2x2−5x−6=(x−3)⋅(x2+5x+10)+24=x3+5x2+10x−3x2−15x−30+24=x3+2x2−5x−6.
P(x)x3+2x2−5x−6====d(x)⋅Q(x)+R(x)(x−3)⋅(x2+5x+10)+24x3+5x2+10x−3x2−15x−30+24x3+2x2−5x−6.

The Remainder Theorem and Synthetic Division

Consider the function

h(x)=x3+2x2−5x−6.
h(x)=x3+2x2−5x−6.

When we divided h(x)h(x) by x+1x+1 and x−3x−3 in Example 1, the remainders were 0 and 24, respectively. Let’s now find the function values h(−1)h(−1) and h(3):h(3):

h(−1)=(−1)3+2(−1)2−5(−1)−6=0;h(3)=(3)3+2(3)2−5(3)−6=24.
h(−1)=(−1)3+2(−1)2−5(−1)−6=0;h(3)=(3)3+2(3)2−5(3)−6=24.

Note that the function values are the same as the remainders. This suggests the following theorem.

Proof (Optional). The equation f(x)=d(x)⋅Q(x)+R(x)f(x)=d(x)⋅Q(x)+R(x), where d(x)=x−cd(x)=x−c, is the basis of this proof. If we divide f(x)f(x) by x−cx−c, we obtain a quotient Q(x)Q(x) and a remainder R(x)R(x) related as follows:

f(x)=(x−c)⋅Q(x)+R(x).
f(x)=(x−c)⋅Q(x)+R(x).

The remainder R(x)R(x) must either be 0 or have degree less than x−cx−c. Thus, R(x)R(x) must be a constant. Let’s call this constant R. The equation above is true for any replacement of x, so we replace x with c. We get

f(c)=(c−c)⋅Q(c)+R=0⋅Q(c)+R=R.
f(c)===(c−c)⋅Q(c)+R0⋅Q(c)+RR.

Thus the function value f(c)f(c) is the remainder obtained when we divide f(x)f(x) by x−cx−c.

The remainder theorem motivates us to find a rapid way of dividing by x−cx−c in order to find function values. To streamline division, we can arrange the work so that duplicate and unnecessary writing is avoided. Consider the following:

(4x3−3x2+x+7)÷(x−2).
(4x3−3x2+x+7)÷(x−2).

  1. 4x2+5x+11x−24x3−3x2+x+74x3−8x2¯5x2+x5x2−10x¯11x+711x−22¯294x2+5x+11x−24x3−3x2+x+74x3−8x2¯¯¯¯¯¯¯¯¯¯¯¯¯¯5x2+x5x2−10x¯¯¯¯¯¯¯¯¯¯¯¯¯¯11x+711x−22¯¯¯¯¯¯¯¯¯¯¯¯¯29

  2. 45111−24−3+1+74−8¯5+15−10¯11+711−22¯2945111−24−3+1+74−8¯¯¯¯¯¯¯¯5+15−10¯¯¯¯¯¯¯¯¯11+711−22¯¯¯¯¯¯¯¯¯¯¯29

    The division in (B) is the same as that in (A), but we wrote only the coefficients. The red numerals are duplicated, so we look for an arrangement in which they are not duplicated. In place of the divisor in the form x−cx−c, we can simply use c and then add rather than subtract. When the procedure is “collapsed,” we have the algorithm known as synthetic division.

  3. Synthetic Division

We “bring down” the 4. Then we multiply it by the 2 to get 8 and add to get 5. We then multiply 5 by 2 to get 10, add, and so on. The last number, 29, is the remainder. The others, 4, 5, and 11, are the coefficients of the quotient, 4x2+5x+114x2+5x+11. (Note that the degree of the quotient is 1 less than the degree of the dividend when the degree of the divisor is 1.)

When using synthetic division, we write a 0 for a missing term in the dividend.

Example 2

Use synthetic division to find the quotient and the remainder:

(2x3+7x2−5) ÷ (x+3).
(2x3+7x2−5) ÷ (x+3).

Solution

First, we note that x+3=x−(−3)x+3=x−(−3).

−3270−5−6−3921−3|4Note: We must write a 0for the missing x-term.
−3227−610−3−3|−594Note: We must write a 0for the missing x-term.

The quotient is 2x2+x−32x2+x−3. The remainder is 4.

Now Try Exercise 13.

We can now use synthetic division to find polynomial function values.

Example 3

Given that f(x)=2x5−3x4+x3−2x2+x−8f(x)=2x5−3x4+x3−2x2+x−8, find f(10)f(10).

Solution

By the remainder theorem, f(10)f(10) is the remainder when f(x)f(x) is divided by x−10x−10. We use synthetic division to find that remainder.

102−31−21−820170171017, 080 170, 810217171170817, 081|170, 802
1022−320171170171−217101708117, 08017, 081|−8 170, 810170, 802

Thus, f(10)=170,802f(10)=170,802.

Now Try Exercise 25.

Compare the computations in Example 3 with those in a direct substitution:

f(10)=2(10)5−3(10)4+(10)3−2(10)2+10−8=2⋅100,000−3⋅10,000+1000−2⋅100+10−8=200,000−30,000+1000−200+10−8=170,802.
f(10)====2(10)5−3(10)4+(10)3−2(10)2+10−82⋅100,000−3⋅10,000+1000−2⋅100+10−8200,000−30,000+1000−200+10−8170,802.

Example 4

Determine whether 5 is a zero of g(x)g(x), where

g(x)=x4−26x2+25.
g(x)=x4−26x2+25.

Solution

We use synthetic division and the remainder theorem to find g(5)g(5).

510−26025525−5 −2515−1−5|0Writing 0’s for missing terms:x4+0x3−26x2+0x+25
511055−2625−10−5−5|25 −250Writing 0’s for missing terms:x4+0x3−26x2+0x+25

Since g(5)=0g(5)=0, the number 5 is a zero of g(x)g(x).

Now Try Exercise 31.

Example 5

Determine whether i is a zero of f(x)f(x), where

f(x)=x3−3x2+x−3.
f(x)=x3−3x2+x−3.

Solution

We use synthetic division and the remainder theorem to find f(i)f(i).

Since f(i)=0f(i)=0, the number i is a zero of f(x)f(x).

Now Try Exercise 35.

Finding Factors of Polynomials

We now consider a useful result that follows from the remainder theorem.

Proof (Optional). If we divide f(x)f(x) by x−cx−c, we obtain a quotient and a remainder, related as follows:

f(x)=(x−c)⋅Q(x)+f(c).
f(x)=(x−c)⋅Q(x)+f(c).

Then if f(c)=0f(c)=0, we have

f(x)=(x−c)⋅Q(x),
f(x)=(x−c)⋅Q(x),

so x−cx−c is a factor of f(x)f(x).

The factor theorem is very useful in factoring polynomials and hence in solving polynomial equations and finding zeros of polynomial functions. If we know a zero of a polynomial function, we know a factor.

Example 6

Let f(x)=x3−3x2−6x+8f(x)=x3−3x2−6x+8. Factor f(x)f(x) and solve the equation f(x)=0f(x)=0.

Solution

We look for linear factors of the form x−cx−c. Let’s try x+1x+1, or x−(−1)x−(−1). (In the next section, we will learn a method for choosing the numbers to try for c.) We use synthetic division to determine whether f(−1)=0f(−1)=0.

−11−3−68−1421−4−2|10
−111−3−1−4−64−2|8210

Since f(−1)≠0f(−1)≠0, we know that x+1x+1 is not a factor of f(x)f(x). We now try x−1x−1.

11−3−681−2−81−2−8|0
111−31−2−6−2−8|8−80

Since f(1)=0f(1)=0, we know that x−1x−1 is one factor of f(x)f(x) and the quotient, x2−2x−8x2−2x−8, is another. Thus,

f(x)=(x−1)(x2−2x−8).
f(x)=(x−1)(x2−2x−8).

The trinomial x2−2x−8x2−2x−8 is easily factored, so we have

f(x)=(x−1)(x−4)(x+2).
f(x)=(x−1)(x−4)(x+2).

Our goal is to solve the equation f(x)=0f(x)=0. To do so, we use the principle of zero products:

(x−1)(x−4)(x+2)=0x−1=0orx−4=0orx+2=0x=1orx=4orx=−2.
(x−1)(x−4)(x+2)=0x−1x==01ororx−4x==04ororx+2x==0−2.

The solutions of the equation x3−3x2−6x+8=0x3−3x2−6x+8=0 are −2, 1, and 4. They are also the zeros of the function f(x)=x3−3x2−6x+8f(x)=x3−3x2−6x+8.

Now Try Exercise 41.

4.3 Exercise Set

  1. 1. For the function

    f(x)=x4−6x3+x2+24x−20,
    f(x)=x4−6x3+x2+24x−20,

    use long division to determine whether each of the following is a factor of f(x)f(x).

    1. x+1x+1

    2. x−2x−2

    3. x+5x+5

  2. 2. For the function

    h(x)=x3−x2−17x−15,
    h(x)=x3−x2−17x−15,

    use long division to determine whether each of the following is a factor of h(x)h(x).

    1. x+5x+5

    2. x+1x+1

    3. x+3x+3

  3. 3. For the function

    g(x)=x3−2x2−11x+12,
    g(x)=x3−2x2−11x+12,

    use long division to determine whether each of the following is a factor of g(x)g(x).

    1. x−4x−4

    2. x−3x−3

    3. x−1x−1

  4. 4. For the function

    f(x)=x4+8x3+5x2−38x+24,
    f(x)=x4+8x3+5x2−38x+24,

    use long division to determine whether each of the following is a factor of f(x)f(x).

    1. x+6x+6

    2. x+1x+1

    3. x−4x−4

In each of the following, a polynomial P(x)P(x) and a divisor d(x)d(x) are given. Use long division to find the quotient Q(x)Q(x) and the remainder R(x)R(x) when P(x)P(x) is divided by d(x)d(x). Express P(x)P(x) in the form d(x)⋅Q(x)+R(x)d(x)⋅Q(x)+R(x).

  1. 5. P(x)=x3−8,d(x)=x+2P(x)d(x)==x3−8,x+2

  2. 6. P(x)=2x3−3x2+x−1,d(x)=x−3P(x)d(x)==2x3−3x2+x−1,x−3

  3. 7. P(x)=x3+6x2−25x+18,d(x)=x+9P(x)d(x)==x3+6x2−25x+18,x+9

  4. 8. P(x)=x3−9x2+15x+25,d(x)=x−5P(x)d(x)==x3−9x2+15x+25,x−5

  5. 9. P(x)=x4−2x2+3,d(x)=x+2P(x)d(x)==x4−2x2+3,x+2

  6. 10. P(x)=x4+6x3,d(x)=x−1P(x)d(x)==x4+6x3,x−1

Use synthetic division to find the quotient and the remainder.

  1. 11. (2x4+7x3+x−12)÷(x+3)(2x4+7x3+x−12)÷(x+3)

  2. 12. (x3−7x2+13x+3)÷(x−2)(x3−7x2+13x+3)÷(x−2)

  3. 13. (x3−2x2−8)÷(x+2)(x3−2x2−8)÷(x+2)

  4. 14. (x3−3x+10)÷(x−2)

  5. 15. (3x3−x2+4x−10)÷(x+1)

  6. 16. (4x4−2x+5)÷(x+3)

  7. 17. (x5+x3−x)÷(x−3)

  8. 18. (x7−x6+x5−x4+2)÷(x+1)

  9. 19. (x4−1)÷(x−1)

  10. 20. (x5+32)÷(x+2)

  11. 21. (2x4+3x2−1)÷(x−12)

  12. 22. (3x4−2x2+2)÷(x−14)

Use synthetic division to find the function values. Then check your work using a graphing calculator.

  1. 23. f(x)=x3−6x2+11x−6; find f(1), f(−2), and f(3).

  2. 24. f(x)=x3+7x2−12x−3; find f(−3), f(−2), and f(1).

  3. 25. f(x)=x4−3x3+2x+8; find f(−1), f(4), and f(−5).

  4. 26. f(x)=2x4+x2−10x+1; find f(−10), f(2), and f(3).

  5. 27. f(x)=2x5−3x4+2x3−x+8; find f(20) and f(−3).

  6. 28. f(x)=x5−10x4+20x3−5x−100; find f(−10) and f(5).

  7. 29. f(x)=x4−16; find f(2), f(−2), f(3), and f(1−√2).

  8. 30. f(x)=x5+32; find f(2), f(−2), f(3), and f(2+3i).

Using synthetic division, determine whether the numbers are zeros of the polynomial function.

  1. 31. −3, 2; f(x)=3x3+5x2−6x+18

  2. 32. −4, 2; f(x)=3x3+11x2−2x+8

  3. 33. −3, 1; h(x)=x4+4x3+2x2−4x−3

  4. 34. 2, −1; g(x)=x4−6x3+x2+24x−20

  5. 35. i, −2i; g(x)=x3−4x2+4x−16

  6. 36. 13, 2; h(x)=x3−x2−19x+19

  7. 37. −3, 12; f(x)=x3−72x2+x−32

  8. 38. i, −i, −2; f(x)=x3+2x2+x+2

Factor the polynomial function f(x). Then solve the equation f(x)=0.

  1. 39. f(x)=x3+4x2+x−6

  2. 40. f(x)=x3+5x2−2x−24

  3. 41. f(x)=x3−6x2+3x+10

  4. 42. f(x)=x3+2x2−13x+10

  5. 43. f(x)=x3−x2−14x+24

  6. 44. f(x)=x3−3x2−10x+24

  7. 45. f(x)=x4−7x3+9x2+27x−54

  8. 46. f(x)=x4−4x3−7x2+34x−24

  9. 47. f(x)=x4−x3−19x2+49x−30

  10. 48. f(x)=x4+11x3+41x2+61x+30

Sketch the graph of the polynomial function. Follow the procedure outlined on p. 240. Use synthetic division and the remainder theorem to find the zeros.

  1. 49. f(x)=x4−x3−7x2+x+6

  2. 50. f(x)=x4+x3−3x2−5x−2

  3. 51. f(x)=x3−7x+6

  4. 52. f(x)=x3−12x+16

  5. 53. f(x)=−x3+3x2+6x−8

  6. 54. f(x)=−x4+2x3+3x2−4x−4

Skill Maintenance

Solve. Find exact solutions. [3.2]

  1. 55. 2x2+12=5x

  2. 56. 7x2+4x=3

Consider the function

g(x)=x2+5x−14

in Exercises 57–59.

  1. 57. What are the inputs if the output is −14? [3.2]

  2. 58. What is the output if the input is 3? [1.2]

  3. 59. Given an output of −20, find the corresponding inputs. [3.2]

  4. 60. Movie Ticket Price. The average price of a movie ticket has increased linearly over the years, rising from $2.69 in 1980 to $8.38 in 2013 (Source: Motion Picture Association of America). Using these two data points, find a linear function, f(x)=mx+b, that models the data. Let x represent the number of years after 1980. Then use this function to estimate the average price of a movie ticket in 1995 and in 2018. [1.4]

  5. 61. The sum of the base and the height of a triangle is 30 in. Find the dimensions for which the area is a maximum. [3.2]

Synthesis

In Exercises 62 and 63, a graph of a polynomial function is given. On the basis of the graph:

  1. Find as many factors of the polynomial as you can.

  2. Construct a polynomial function with the zeros shown in the graph.

  3. Can you find any other polynomial functions with the given zeros?

  4. Can you find any other polynomial functions with the given zeros and the same graph?

  1. 62.

  2. 63.

  3. 64. For what values of k will the remainder be the same when x2+kx+4 is divided by x−1 and by x+1?

  4. 65. Find k such that x+2 is a factor of x3−kx2+3x+7k.

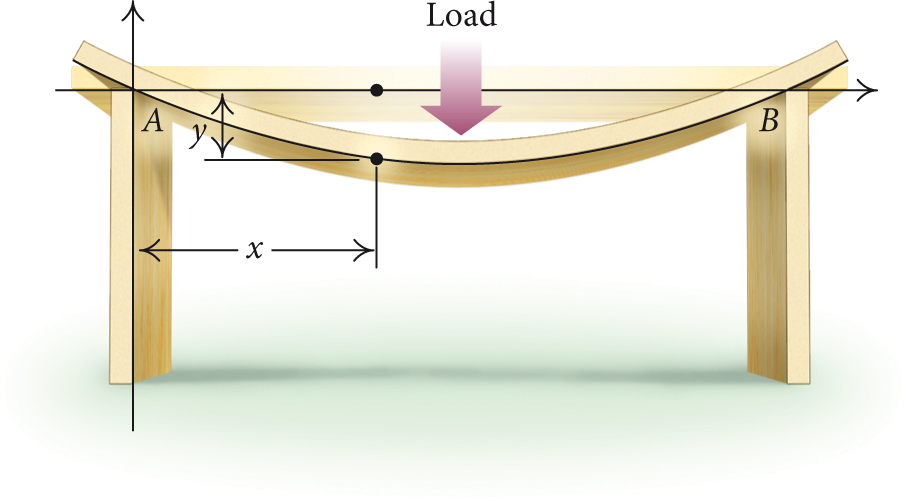
  5. 66. Beam Deflection. A beam rests at two points A and B and has a concentrated load applied to its center, as shown below. Let y= the deflection, in feet, of the beam at a distance of x feet from A. Under certain conditions, this deflection is given by

    y=113x3−114x.

    Find the zeros of the polynomial in the interval [0, 2].

Solve.

  1. 67. 2x2x2−1+4x+3=12x−4x3+3x2−x−3

  2. 68. 6x2x2+11+60x3−7x2+11x−77=1x−7

  3. 69. Find a 15th-degree polynomial for which x−1 is a factor. Answers may vary.

Use synthetic division to divide.

  1. 70. (x4−y4)÷(x−y)

  2. 71. (x3+3ix2−4ix−2)÷(x+i)

  3. 72. (x2−4x−2)÷[x−(3+2i)]

  4. 73. (x2−3x+7)÷(x−i)

..................Content has been hidden....................

You can't read the all page of ebook, please click here login for view all page.
Reset