Search in book...
Toggle Font Controls
Create new playlist

Name your new playlist

Playlist description (optional)
Sign In

Email address

Password

Forgot Password?

or

Continue with Facebook

Continue with Google
Sign Up

Full Name

Email address

Confirm Email Address

Password

or

Continue with Facebook

Continue with Google

Just-In-Time Review

Throughout this text, there are Just-In-Time icons, numbered 1–25, that refer to the following 25 intermediate-algebra topics. Each mini-review lesson is accompanied by several exercises. All answers are provided in the answer section at the back of the text.

Real Numbers

Some frequently used sets of real numbers and the relationships among them are shown in the following diagram.

Numbers that can be expressed in the form p/q, where p and q are integers and $q \neq 0$ , are rational numbers. Decimal notation for rational numbers either terminates (ends) or repeats. Each of the following is a rational number:

$\begin{array}{l} 0, & - 17, & \frac{13}{4}, & \sqrt{25} = 5; \end{array}$

$\begin{array}{l} \frac{1}{4} = 0.25 & (terminating decimal); \end{array}$

$\begin{array}{l} - \frac{5}{11} = - 0.454545 \dots = - 0. \bar{45} & (repeating decimal); \end{array}$

$\begin{array}{l} \frac{5}{6} = 0.8333 \dots = 0.8 \bar{3} & (repeating decimal) . \end{array}$

The real numbers that are not rational are irrational numbers. Decimal notation for irrational numbers neither terminates nor repeats. Each of the following is an irrational number. Note in each that there is no repeating block of digits.

$\sqrt{2} = 1.414213562 \dots,$

$- 6.12122122212222 \dots,$

$π = 3.1415926535 \dots$

$(\frac{22}{7} and 3.14 are rational approximations of the irrational number π .)$

The set of all rational numbers combined with the set of all irrational numbers gives us the set of real numbers.

Do Exercises 1–6.

In Exercises 1–6, consider the numbers

$\frac{2}{3}, 6, \sqrt{3}, - 2.45, \sqrt[6]{26}, 18. \bar{4},$

$- 11, \sqrt[3]{27}, 5 \frac{1}{6}, 7.151551555 \dots,$

$- \sqrt{35}, \sqrt[5]{3}, - \frac{8}{7}, 0, \sqrt{16} .$

Which are rational numbers?
Which are rational numbers but not integers?
Which are irrational numbers?
Which are integers?
Which are whole numbers?
Which are real numbers?

Properties of Real Numbers

For any real numbers a, b, and c:

$\begin{array}{l} a + b = b + a and a b = b a & Commutative properties of addition and multiplication \\ a + (b + c) = (a + b) + c and a (b c) = (a b) c & Associative properties of addition and multiplication \\ a + 0 = 0 + a = a & Additive identity property \\ - a + a = a + (- a) = 0 & Additive inverse property \\ a \cdot 1 = 1 \cdot a = a & Multiplicative identity property \\ a \cdot \frac{1}{a} = \frac{1}{a} \cdot a = 1 (a \neq 0) & Multiplicative inverse property \\ a (b + c) = a b + a c and a (b - c) = a b - a c & Distributive properties \end{array}$

Examples

Name the property illustrated in each sentence.

$\begin{array}{l} 1. & 8 \cdot 5 = 5 \cdot 8 & Commutative property of multiplication \\ 2. & 14 + (- 14) = 0 & Additive inverse property \\ 3. & 2 (a - b) = 2 a - 2 b & Distributive property \\ 4. & 5 + (m + n) = (5 + m) + n & Associative property of addition \\ 5. & 6 \cdot 1 = 1 \cdot 6 = 6 & Multiplicative identity property \end{array}$

Do Exercises 1–10.

Name the property illustrated by the sentence.

$- 24 + 24 = 0$
$7 (x y) = 7 (x) y$
$9 (r - s) = 9 r - 9 s$
$11 + z = z + 11$
$- 20 \cdot 1 = - 20$
$5 (x + y) = (x + y) 5$
$q + 0 = q$
$75 \cdot \frac{1}{75} = 1$
$(x + y) + w = x + (y + w)$
$8 (a + b) = 8 a + 8 b$

Absolute Value

The absolute value of a number a, denoted $| a |$ , is its distance from 0 on the number line. For example, $| - 5 | = 5$ , because the distance of −5 from 0 is 5. For any real number a,

$| a | = a if a \geq 0$

and

$| a | = - a if a < 0.$

Examples

Simplify.

$| - 10 | = 10$
$| 0 | = 0$
$| \frac{4}{9} | = \frac{4}{9}$

Absolute value can be used to find the distance between two points on the number line. For any real numbers a and b, the distance between a and b is $| a - b |$ or, equivalently, $| b - a |$ .

Example 4

Find the distance between −2 and 3.

$| - 2 - 3 | = | - 5 | = 5,$

or equivalently,

$| 3 - (- 2) | = | 3 + 2 | = | 5 | = 5$

Do Exercises 1–8.

Simplify.

$| - 98 |$
$| 0 |$
$| 4.7 |$
$| - \frac{2}{3} |$

Find the distance between the given pair of points on the number line.

−7, 13
2, 14.6
−39, −28
$- \frac{3}{4}, \frac{15}{8}$

Operations with Real Numbers

Rules for Operations with Real Numbers

Addition

Positive Numbers: Add the same way that we add arithmetic numbers. The answer is positive.
Negative Numbers: Add absolute values. The answer is negative.
A Positive Number and a Negative Number: If the numbers have different absolute values, subtract the smaller absolute value from the larger. If the positive number has the greater absolute value, the answer is positive. If the negative number has the greater absolute value, the answer is negative.

Examples

Add.

$9 + (- 29) = - 20$
$- 9 + (- 29) = - 38$
$- 9 + 29 = 20$

Subtraction

To subtract, add the opposite, or additive inverse, of the number being subtracted.

Examples

Subtract.

$15 - 6 = 15 + (- 6) = 9$
$15 - (- 6) = 15 + 6 = 21$
$- 15 - 6 = - 15 + (- 6) = - 21$
$- 15 - (- 6) = - 15 + 6 = - 9$

Multiplication and Division, where the divisor is nonzero

Multiply or divide the absolute values. If the signs are the same, the answer is positive. If the signs are different, the answer is negative.

Examples

Multiply or divide.

$- 5 \cdot 20 = - 100$
$32 \div (- 4) = - 8$
$- 32 \div 4 = - 8$
$- 32 \div (- 4) = 8$
$- 5 \cdot (- 20) = 100$
$5 \cdot 20 = 100$

Do Exercises 1–15.

Compute and simplify.

$8 - (- 11)$
$- \frac{3}{10} \cdot (- \frac{1}{3})$
$15 \div (- 3)$
$- 4 - (- 1)$
$7 \cdot (- 50)$
$- 0.5 - 5$
$- 3 + 27$
$- 400 \div (- 40)$
$4.2 \cdot (- 3)$
$- 13 - (- 33)$
$- 60 + 45$
$\frac{1}{2} - \frac{2}{3}$
$- 24 \div 3$
$- 6 + (- 16)$
$- \frac{1}{2} \div (- \frac{5}{8})$

Order on the Number Line

The real numbers are modeled using a number line, as shown below. Each point on the line represents a real number, and every real number is represented by a point on the line.

The order of the real numbers can be determined from the number line. If a number a is to the left of a number b, then a is less than b $(a < b)$ . Similarly, a is greater than b $(a > b)$ if a is to the right of b on the number line. For example, we see from the number line above that $- 2.9 < - \frac{3}{5}$ , because −2.9 is to the left of $- \frac{3}{5}$ . Also, $\frac{17}{4} >$ $\sqrt{3}$ , because $\frac{17}{4}$ is to the right of $\sqrt{3}$ .

The statement $a \leq b$ , read “a is less than or equal to b,” is true if either $a < b$ is true or $a = b$ is true. A similar statement holds for $a \geq b$ .

Do Exercises 1–6.

Classify the inequality as true or false.

$9 < - 9$
$- 10 \leq - 1$
$- \sqrt{26} < - 5$
$\sqrt{6} \geq \sqrt{6}$
$- 30 > - 25$
$- \frac{4}{5} > - \frac{5}{4}$

Interval Notation

Sets of real numbers can be expressed using interval notation. For example, for real numbers a and b such that $a < b$ , the open interval (a, b) is the set of real numbers between, but not including, a and b.

Some intervals extend without bound in one or both directions. The interval $[a, \infty)$ , for example, begins at a and extends to the right without bound. The bracket indicates that a is included in the interval.

SET NOTATION	INTERVAL NOTATION	GRAPH
${x \| a < x < b}$	(`a`, `b`)
${x \| a \leq x \leq b}$	$[a, b]$
${x \| a \leq x < b}$	$[a, b)$
${x \| a < x \leq b}$	$(a, b]$
${x \| x > a}$	$(a, \infty)$
${x \| x \geq a}$	$[a, \infty)$
${x \| x < b}$	$(- \infty, b)$
${x \| x \leq b}$	$(- \infty, b]$
${x \| x is a real number}$	$(- \infty, \infty)$

Do Exercises 1–10.

Write interval notation.

${x | - 5 \leq x \leq 5}$
${x | - 3 < x \leq - 1}$
${x | x \leq - 2}$
${x | x > 3.8}$
${x | 7 < x}$
${x | - 2 < x < 2}$

Write interval notation for the graph.

Integers as Exponents

When a positive integer is used as an exponent, it indicates the number of times that a factor appears in a product. For example, $7^{3}$ means $7 \cdot 7 \cdot 7$ , where 7 is the base and 3 is the exponent.

For any nonzero numbers a and b and any integers m and n,

$a^{0} = 1, a^{- m} = \frac{1}{a^{m}}, and \frac{a^{- m}}{b^{- n}} = \frac{b^{n}}{a^{m}} .$

Properties of Exponents

For any real numbers a and b and any integers m and n, assuming 0 is not raised to a nonpositive power:

$a^{m} \cdot a^{n} = a^{m + n}$	Product rule
$\frac{a^{m}}{a^{n}} = a^{m - n} (a \neq 0)$	Quotient rule
${(a^{m})}^{n} = a^{m n}$	Power rule
${(a b)}^{m} = a^{m} b^{m}$	Raising a product to a power
${(\frac{a}{b})}^{m} = \frac{a^{m}}{b^{m}} (b \neq 0)$	Raising a quotient to a power

Examples

Simplify each of the following.

$4^{2} \cdot 4^{- 5} = 4^{2 + (- 5)} = 4^{- 3}$ , or $\frac{1}{4^{3}}$
${(\frac{7}{9})}^{0} = 1$
${(8^{2})}^{- 5} = 8^{2 (- 5)} = 8^{- 10}$ , or $\frac{1}{8^{10}}$
$\frac{x^{11}}{x^{4}} = x^{11 - 4} = x^{7}$
${(\frac{a}{b})}^{3} = \frac{a^{3}}{b^{3}}$
${(c d)}^{- 2} = c^{- 2} d^{- 2}$ , or $\frac{1}{c^{2} d^{2}}$

Do Exercises 1–10.

Simplify.

$3^{- 6}$
$\frac{1}{{(0.2)}^{- 5}}$
$\frac{w^{- 4}}{z^{- 9}}$
${(\frac{z}{y})}^{2}$
$100^{0}$
$\frac{a^{5}}{a^{- 3}}$
$(2 x y^{3}) (- 3 x^{- 5} y)$
$x^{- 4} \cdot x^{- 7}$
${(m n)}^{- 6}$
${(t^{- 5})}^{4}$

Scientific Notation

We can use scientific notation to name both very large and very small positive numbers and to perform computations. Scientific notation for a number is an expression of the type $N \times 10^{m}$ , where $1 \leq N < 10$ , N is in decimal notation, and m is an integer.

Examples

Convert to scientific notation.

$\begin{array}{l} 1. & 9,460,000,000,000 = 9.46 \times 10^{12} & Large number; exponent is positive . \\ 2. & 0.0648 = 6.48 \times 10^{- 2} & Small number; exponent is negative . \end{array}$

Convert to decimal notation.

$5.4 \times 10^{7} = 54,000,000$
$3.819 \times 10^{- 3} = 0.003819$

Do Exercises 1–8.

Convert to scientific notation.

18,500,000
0.000786
0.0000000023
8,927,000,000

Convert to decimal notation.

$4.3 \times 10^{- 8}$
$5.17 \times 10^{6}$
$6.203 \times 10^{11}$
$2.94 \times 10^{- 5}$

Order of Operations

Recall that to simplify the expression $3 + 4 \cdot 5$ , first we multiply 4 and 5 to get 20 and then we add 3 to get 23. Mathematicians have agreed on the following procedure, or rules for order of operations.

Rules for Order of Operations

Do all calculations within grouping symbols before operations outside. When nested grouping symbols are present, work from the inside out.
Evaluate all exponential expressions.
Do all multiplications and divisions in order from left to right.
Do all additions and subtractions in order from left to right.

Examples

$\begin{array}{l} 1. 8 {(5 - 3)}^{3} - 20 \\ = 8 \cdot 2^{3} - 20 \\ = 8 \cdot 8 - 20 \\ = 64 - 20 \\ = 44 \end{array}$

$\begin{array}{l} 2. \frac{10 \div (8 - 6) + 9.4}{2^{5} + 3^{2}} \\ = \frac{10 \div 2 + 9 \cdot 4}{32 + 9} \\ = \frac{5 + 36}{41} = \frac{41}{41} = 1 \end{array}$

Do Exercises 1–6.

Calculate.

$3 + 18 \div 6 - 3$
$5 \cdot 3 + 8 \cdot 3^{2} + 4 (6 - 2)$
$5 (3 - 8 \cdot 3^{2} + 4 \cdot 6 - 2)$
$16 \div 4 \cdot 4 \div 2 \cdot 256$
$2^{6} \cdot 2^{- 3} \div 2^{10} \div 2^{- 8}$
$\frac{4 {(8 - 6)}^{2} - 4 \cdot 3 + 2 \cdot 8}{3^{1} + 19^{0}}$

Introduction to Polynomials

Polynomials are a type of algebraic expression that you will often encounter in your study of algebra. Some examples of polynomials are

$\begin{array}{l} 3 x - 4 y, 5 y^{3} - \frac{7}{3} y^{2} + 3 y - 2, - 2.3 a^{4}, \\ 16, and z^{6} - \sqrt{5} . \end{array}$

Algebraic expressions like $8 x - 13, x^{2} + 3 x - 4$ , and $3 a^{5} - 11 + a$ are polynomials in one variable. Algebraic expressions like $3 a b^{3} - 8$ and $5 x^{4} y^{2} - 3 x^{3} y^{8} + 7 x y^{2} + 6$ are polynomials in several variables. The degree of a term is the sum of the exponents of the variables in that term. The degree of a polynomial is the degree of the term of highest degree.

A polynomial with just one term, like $- 9 y^{6}$ , is a monomial. If a polynomial has two terms, like $x^{2} + 4$ , it is a binomial. A polynomial with three terms, like $4 x^{2} - 4 x y + 1$ , is a trinomial.

Examples

Determine the degree of the polynomial.

$2 x^{3} - 1$ Degree: 3
$- 5 (- 5 = - 5 x^{0})$ Degree: 0
$w^{2} - 3.5 + 4 w^{5} = 4 w^{5} + w^{2} - 3.5$ Degree: 5
$7 x y^{3} - 16 x^{2} y^{4}$ Degree: 2 $+$ 4, or 6

Do Exercises 1–8.

Determine the degree of the polynomial.

$5 - x^{6}$
$x^{2} y^{5} - x^{7} y + 4$
$2 a^{4} - 3 + a^{2}$
−41
$4 x - x^{3} + 0.1 x^{8} - 2 x^{5}$

Classify the polynomial as a monomial, a binomial, or a trinomial.

$x - 3$
$14 y^{5}$
$2 y - \frac{1}{4} y^{2} + 8$

Add and Subtract Polynomials

If two terms of an expression have the same variables raised to the same powers, they are called like terms, or similar terms. We can combine, or collect, like terms using the distributive property. For example, $3 y^{2}$ and $5 y^{2}$ are like terms and $3 y^{2} + 5 y^{2} = (3 + 5) y^{2}$ . We add or subtract polynomials by combining like terms.

Examples

Add or subtract each of the following.

$\begin{array}{l} 1. & (- 5 x^{3} + 3 x^{2} - x) + (12 x^{3} - 7 x^{2} + 3) \\ = (- 5 x^{3} + 12 x^{3}) + (3 x^{2} - 7 x^{2}) - x + 3 \\ = (- 5 + 12) x^{3} + (3 - 7) x^{2} - x + 3 = 7 x^{3} - 4 x^{2} - x + 3 \\ 2. & (6 x^{2} y^{3} - 9 x y) - (5 x^{2} y^{3} - 4 x y) \\ = (6 x^{2} y^{3} - 9 x y) + (- 5 x^{2} y^{3} + 4 x y) \\ = 6 x^{2} y^{3} - 9 x y - 5 x^{2} y^{3} + 4 x y = x^{2} y^{3} - 5 x y \end{array}$

Do Exercises 1–5.

Add or subtract.

$(8 y - 1) - (3 - y)$
$\begin{array}{l} (3 x^{2} - 2 x - x^{3} + 2) - (5 x^{2} - 8 x - x^{3} + 4) \end{array}$
$(2 x + 3 y + z - 7) + (4 x - 2 y - z + 8) + (- 3 x + y - 2 z - 4)$
$(3 a b^{2} + 4 a^{2} b - 2 a b + 6) + (- a b^{2} - 5 a^{2} b + 8 a b + 4)$
$(5 x^{2} + 4 x y - 3 y^{2} + 2) - (9 x^{2} - 4 x y + 2 y^{2} - 1)$

Multiply Polynomials

To multiply monomials, we first multiply their coefficients, and then we multiply their variables.

Examples

$(- 2 x^{3}) (5 x^{4}) = (- 2 \cdot 5) (x^{3} \cdot x^{4}) = - 10 x^{7}$
$(3 y z^{2}) (8 y^{3} z^{5}) = (3 \cdot 8) (y \cdot y^{3}) (z^{2} \cdot z^{5}) = 24 y^{4} z^{7}$

We can find the product of two binomials by multiplying the First terms, then the Outer terms, then the Inner terms, then the Last terms. Then we combine like terms, if possible. This procedure is sometimes called FOIL.

Example 3

Multiply: $(2 x - 7) (3 x + 4)$ .

Special Products of Binomials

${(A + B)}^{2} = A^{2} + 2 A B + B^{2}$	Square of a sum
${(A - B)}^{2} = A^{2} - 2 A B + B^{2}$	Square of a difference
$(A + B) (A - B) = A^{2} - B^{2}$	Product of a sum and a difference

Examples

$\begin{array}{rcl} {(4 x + 1)}^{2} & = & {(4 x)}^{2} + 2 \cdot 4 x \cdot 1 + 1^{2} \\ = & 16 x^{2} + 8 x + 1 \end{array}$
$\begin{array}{rcl} {(3 y^{2} - 2)}^{2} & = & {(3 y^{2})}^{2} - 2 \cdot 3 y^{2} \cdot 2 + 2^{2} \\ = & 9 y^{4} - 12 y^{2} + 4 \end{array}$
$\begin{array}{l} (x^{2} + 3 y) (x^{2} - 3 y) & = & {(x^{2})}^{2} - {(3 y)}^{2} \\ = & x^{4} - 9 y^{2} \end{array}$

Do Exercises 1–10.

Multiply.

$(3 a^{2}) (- 7 a^{4})$
$(y - 3) (y + 5)$
$(x + 6) (x + 3)$
$(2 a + 3) (a + 5)$
$(2 x + 3 y) (2 x + y)$
${(x + 3)}^{2}$
${(5 x - 3)}^{2}$
${(2 x + 3 y)}^{2}$
$(n + 6) (n - 6)$
$(3 y + 4) (3 y - 4)$

Factor Polynomials

When a polynomial is to be factored, we should always look first to factor out a factor that is common to all the terms using the distributive property. We generally look for the constant common factor with the largest absolute value and for variables with the largest exponent common to all the terms.

Example 1

Factor: $15 + 10 x - 5 x^{2}$ .

$15 + 10 x - 5 x^{2} = 5 \cdot 3 + 5 \cdot 2 x - 5 \cdot x^{2} = 5 (3 + 2 x - x^{2})$

In some polynomials, pairs of terms have a common binomial factor that can be removed in a process called factoring by grouping.

Example 2

Factor: $x^{3} + 3 x^{2} - 5 x - 15$ .

$\begin{array}{rcl} x^{3} + 3 x^{2} - 5 x - 15 & = & (x^{3} + 3 x^{2}) + (- 5 x - 15) \\ = & x^{2} (x + 3) - 5 (x + 3) \\ = & (x + 3) (x^{2} - 5) \end{array}$

Some trinomials can be factored into the product of two binomials. To factor a trinomial of the form $x^{2} + b x + c$ , we look for binomial factors of the form $(x + p) (x + q)$ , where $p \cdot q = c$ and $p + q = b$ . That is, we look for two numbers p and q whose sum is the coefficient of the middle term of the polynomial, b, and whose product is the constant term, c.

Examples

Factor.

$x^{2} + 5 x + 6 = (x + 2) (x + 3)$
$x^{4} - 6 x^{3} + 8 x^{2} = x^{2} (^{} x^{2} - 6 x + 8) = x^{2} (x - 2) (x - 4)$

To factor trinomials of the type $a x^{2} + b x + c, a \neq 1$ , using the FOIL method:

Factor out the largest common factor.
Find two First terms whose product is $a x^{2} :$
Find two Last terms whose product is c:
Repeat steps (2) and (3) until a combination is found for which the sum of the Outer product and the Inner product is bx:

Examples

Factor.

$3 x^{2} - 10 x - 8 = (3 x + 2) (x - 4)$
$12 y^{2} + 44 y - 45 = (2 y + 9) (6 y - 5)$

Special Factorizations

Examples

$\begin{array}{l} A^{2} - B^{2} = (A + B) (A - B) : \\ x^{2} - 16 = x^{2} - 4^{2} = (x + 4) (x - 4) \end{array}$
$\begin{array}{l} A^{2} + 2 A B + B^{2} = {(A + B)}^{2} : \\ x^{2} + 8 x + 16 = x^{2} + 2 \cdot x \cdot 4 + 4^{2} = {(x + 4)}^{2} \end{array}$
$\begin{array}{l} A^{2} - 2 A B + B^{2} = {(A - B)}^{2} \\ 25 y^{2} - 30 y + 9 = {(5 y)}^{2} - 2 \cdot 5 y \cdot 3 + 3^{2} \\ = {(5 y - 3)}^{2} \end{array}$
$\begin{array}{l} A^{3} + B^{3} = (A + B) (A^{2} - A B + B^{2}) : \\ x^{3} + 27 = x^{3} + 3^{3} = (x + 3) (x^{2} - 3 x + 9) \end{array}$
$\begin{array}{l} A^{3} - B^{3} = (A - B) (A^{2} + A B + B^{2}) : \\ 16 y^{3} - 250 = 2 (8 y^{3} - 125) = 2 [{(2 y)}^{3} - 5^{3}] \\ = 2 (2 y - 5) (4 y^{2} + 10 y + 25) \end{array}$

Do Exercises 1–20.

Factor out the largest common factor.

$3 x + 18$
$2 z^{3} - 8 z^{2}$

Factor by grouping.

$3 x^{3} - x^{2} + 18 x - 6$
$t^{3} + 6 t^{2} - 2 t - 12$

Factor the trinomial.

$w^{2} - 7 w + 10$
$t^{2} + 8 t + 15$
$2 n^{2} - 20 n - 48$
$y^{4} - 9 y^{3} + 14 y^{2}$
$2 n^{2} + 9 n - 56$
$2 y^{2} + y - 6$

Factor the difference of squares.

$z^{2} - 81$
$16 x^{2} - 9$
$7 p q^{4} - 7 p y^{4}$

Factor the square of a binomial.

$x^{2} + 12 x + 36$
$9 z^{2} - 12 z + 4$
$a^{3} + 24 a^{2} + 144 a$

Factor the sum or the difference of cubes.

$x^{3} + 64$
$m^{3} - 216$
$3 a^{5} - 24 a^{2}$
$t^{6} + 1$

Equation-Solving Principles

For any real numbers a, b, and c,

The Addition Principle

If $a = b$ is true, then $a + c = b + c$ is true.

The Multiplication Principle

If $a = b$ is true, then $a c = b c$ is true.

Examples

Solve.

$\begin{array}{rcl} y - 11 & = & 12 \\ y - 11 + 11 & = & 12 + 11 \\ y & = & 23 \end{array}$
$\begin{array}{rcl} 15 c & = & 90 \\ \frac{1}{15} \cdot 15 c & = & \frac{1}{15} \cdot 90 \\ c & = & 6 \end{array}$
$\begin{array}{rcl} \frac{1}{4} x + 5 & = & 8 \\ \frac{1}{4} x + 5 - 5 & = & 8 - 5 \\ \frac{1}{4} x & = & 3 \\ 4 \cdot \frac{1}{4} x & = & 4 \cdot 3 \\ x & = & 12 \end{array}$
$\begin{array}{rcl} 2 x + 3 & = & 1 - 6 (x - 1) \\ 2 x + 3 & = & 1 - 6 x + 6 \\ 2 x + 3 & = & 7 - 6 x \\ 8 x + 3 & = & 7 \\ 8 x & = & 4 \\ x & = & \frac{1}{2} \end{array}$

Do Exercises 1–8.

Solve.

$7 t = 70$
$x - 5 = 7$
$3 x + 4 = - 8$
$6 x - 15 = 45$
$7 y - 1 = 23 - 5 y$
$3 m - 7 = - 13 + m$
$2 (x + 7) = 5 x + 14$
$5 y - 4 (2 y - 10) = 25$

Inequality-Solving Principles

For any real numbers a, b, and c:

The Addition Principle for Inequalities

If $a < b$ is true, then $a + c < b + c$ is true.

The Multiplication Principle for Inequalities

If $a < b$ and $c > 0$ are true, then $a c < b c$ is true.
If $a < b$ and $c < 0$ are true, then $a c > b c$ is true.

(When both sides of an inequality are multiplied by a negative number, the inequality sign must be reversed.)

Similar statements hold for $a \leq b$ .

Examples

Solve.

$\begin{array}{rcl} a + 9 & \leq & - 50 \\ a + 9 - 9 & \leq & - 50 - 9 \\ a & \leq & - 59 \end{array}$
$\begin{array}{rcl} - 5 x & > & 4 \\ - \frac{1}{5} (- 5 x) & < & - \frac{1}{5} (4) \\ x & < & - \frac{4}{5} \end{array}$
$\begin{array}{rcl} 2 y - 1 & < & 5 \\ 2 y - 1 + 1 & < & 5 + 1 \\ 2 y & < & 6 \\ \frac{1}{2} \cdot 2 y & < & \frac{1}{2} \cdot 6 \\ y & < & 3 \end{array}$
$\begin{array}{rcl} 4 - 3 x & \geq & 13 \\ - 4 + 4 - 3 x & \geq & - 4 + 13 \\ - 3 x & \geq & 9 \\ \frac{- 3 x}{- 3} & \leq & \frac{9}{- 3} \\ x & \leq & - 3 \end{array}$

Do Exercises 1–6.

Solve.

$p + 25 \geq - 100$
$- \frac{2}{3} x > 6$
$9 x - 1 < 17$
$- x - 16 \geq 40$
$\frac{1}{3} y - 6 < 3$
$8 - 2 w \leq - 14$

Principle of Zero Products

The product of two numbers is 0 if one or both of the numbers is 0. Furthermore, if any product is 0, then a factor must be 0. For example:

If $7 x = 0$ , then we know that $x = 0$ .
If $x (2 x - 9) = 0$ , then we know that $x = 0$ or $2 x - 9 = 0$ .
If $(x + 3) (x - 2) = 0$ , then we know that $x + 3 = 0$ or $x - 2 = 0$ .

The Principle of Zero Products

If $a b = 0$ is true, then $a = 0$ or $b = 0$ , and if $a = 0$ or $b = 0$ , then $a b = 0$ .

Some quadratic equations can be solved using the principle of zero products.

Examples

Solve.

$\begin{array}{l} \begin{array}{rcl} x^{2} - 3 x - 4 & = & 0 \\ (x + 1) (x - 4) & = & 0 \end{array} \\ \begin{array}{rclcrcl} x + 1 & = & 0 & or & x - 4 & = & 0 \\ x & = & - 1 & or & x & = & 4 \end{array} \end{array}$

The solutions are −1 and 4.
$\begin{array}{l} \begin{array}{rcl} 2 x^{2} + 5 x - 3 & = & 0 \\ (x + 3) (2 x - 1) & = & 0 \end{array} \\ \begin{array}{rclcrcl} x + 3 & = & 0 & or & 2 x - 1 & = & 0 \\ x & = & - 3 & or & 2 x & = & 1 \\ x & = & - 3 & or & x & = & \frac{1}{2} \end{array} \end{array}$

The solutions are −3 and $\frac{1}{2}$ .

Do Exercises 1–7.

Solve.

$(a + 7) (a - 1) = 0$
$(5 y + 3) (y - 4) = 0$
$6 x^{2} + 7 x - 5 = 0$
$t (t - 8) = 0$
$x^{2} - 8 x - 33 = 0$
$x^{2} + 13 x = 30$
$12 x^{2} - 7 x - 12 = 0$

Principle of Square Roots

The principle of square roots can be used to solve some quadratic equations.

The Principle of Square Roots

If $x^{2} = k$ , then $x = \sqrt{k}$ or $x = - \sqrt{k}$ .

Examples

Solve.

$\begin{array}{l} \begin{array}{rcl} s^{2} - 144 & = & 0 \\ s^{2} & = & 144 \end{array} \\ \begin{array}{rclcrcl} s & = & - \sqrt{144} & or & s & = & \sqrt{144} \\ s & = & - 12 & or & s & = & 12 \end{array} \end{array}$

The solutions are −12 and 12, or $\pm 12$ .
$\begin{array}{l} \begin{array}{rcl} 3 x^{2} - 21 & = & 0 \\ 3 x^{2} & = & 21 \\ x^{2} & = & 7 \end{array} \\ x = - \sqrt{7} or x = \sqrt{7} \end{array}$

The solutions are $- \sqrt{7}$ and $\sqrt{7}$ , or $\pm \sqrt{7}$ .

Do Exercises 1–6.

Solve.

$x^{2} - 36 = 0$
$2 y^{2} - 20 = 0$
$6 z^{2} = 18$
$3 t^{2} - 15 = 0$
$z^{2} - 1 = 24$
$5 x^{2} - 75 = 0$

Simplify Rational Expressions

A rational expression is the quotient of two polynomials. The domain of an algebraic expression is the set of all real numbers for which the expression is defined. Since division by 0 is not defined, any number that makes the denominator 0 is not in the domain of a rational expression.

Example 1

Find the domain of

$\frac{x^{2} - 4}{x^{2} - 4 x - 5} .$

We solve the equation $x^{2} - 4 x - 5 = 0$ , or $(x + 1) (x - 5) = 0$ , to find the numbers that are not in the domain. The solutions are −1 and 5. Since the denominator is 0 when $x = - 1$ or $x = 5$ , the domain is the set of all real numbers except −1 and 5.

Examples

Simplify.

$\begin{array}{rcl} \frac{9 x^{2} + 6 x - 3}{12 x^{2} - 12} & = & \frac{3 (3 x^{2} + 2 x - 1)}{12 (x^{2} - 1)} \\ = & \frac{3 (x + 1) (3 x - 1)}{3 \cdot 4 (x + 1) (x - 1)} \\ = & \frac{3 (x + 1)}{3 (x + 1)} \cdot \frac{3 x - 1}{4 (x - 1)} \\ = & 1 \cdot \frac{3 x - 1}{4 (x - 1)} \\ = & \frac{3 x - 1}{4 (x - 1)} \end{array}$

Canceling is a shortcut that is often used to remove a factor of 1.
$\begin{array}{l} \frac{2 - x}{x^{2} + x - 6} & = & \frac{2 - x}{(x + 3) (x - 2)} \\ = & \frac{- 1 (x - 2)}{(x + 3) (x - 2)} \\ = & \frac{- 1 (x - 2)}{(x + 3) (x - 2)} \\ = & \frac{- 1}{x + 3}, or - \frac{1}{x + 3} \end{array}$

Do Exercises 1–6.

Find the domain of the rational expression.

$\frac{3 x - 3}{x (x - 1)}$
$\frac{y + 6}{y^{2} + 4 y - 21}$

Simplify.

$\frac{x^{2} - 4}{x^{2} - 4 x + 4}$
$\frac{x^{2} + 2 x - 3}{x^{2} - 9}$
$\frac{x^{3} - 6 x^{2} + 9 x}{x^{3} - 3 x^{2}}$
$\frac{6 y^{2} + 12 y - 48}{3 y^{2} - 9 y + 6}$

Multiply and Divide Rational Expressions

To multiply rational expressions, we multiply numerators and multiply denominators and, if possible, simplify the result. To divide rational expressions, we multiply the dividend by the reciprocal of the divisor and, if possible, simplify the result; that is,

$\frac{a}{b} \cdot \frac{c}{d} = \frac{a c}{b d} and \frac{a}{b} \div \frac{c}{d} = \frac{a}{b} \cdot \frac{d}{c} = \frac{a d}{b c} .$

Examples

Multiply or divide.

$\begin{array}{rcl} \frac{a^{2} - 4}{16 a} \cdot \frac{20 a^{2}}{a + 2} & = & \frac{(a^{2} - 4) (20 a^{2})}{16 a (a + 2)} \\ = & \frac{(a + 2) (a - 2) \cdot 4 \cdot 5 \cdot a \cdot a}{4 \cdot 4 \cdot a \cdot (a + 2)} \\ = & \frac{5 a (a - 2)}{4} \end{array}$
$\begin{array}{l} \frac{x - 2}{12} \div \frac{x^{2} - 4 x + 4}{3 x^{3} + 15 x^{2}} & = & \frac{x - 2}{12} \cdot \frac{3 x^{3} + 15 x^{2}}{x^{2} - 4 x + 4} \\ = & \frac{(x - 2) (3 x^{3} + 15 x^{2})}{12 (x^{2} - 4 x + 4)} \\ = & \frac{(x - 2) (3) (x^{2}) (x + 5)}{3 \cdot 4 (x - 2) (x - 2)} \\ = & \frac{x^{2} (x + 5)}{4 (x - 2)} \end{array}$

Do Exercises 1–6.

Multiply or divide and, if possible, simplify.

$\frac{r - s}{r + s} \cdot \frac{r^{2} - s^{2}}{{(r - s)}^{2}}$
$\frac{m^{2} - n^{2}}{r + s} \div \frac{m - n}{r + s}$
$\frac{4 x^{2} + 9 x + 2}{x^{2} + x - 2} \cdot \frac{x^{2} - 1}{3 x^{2} + x - 2}$
$\frac{a^{2} - a - 2}{a^{2} - a - 6} \div \frac{a^{2} - 2 a}{2 a + a^{2}}$
$\frac{3 x + 12}{2 x - 8} \div \frac{{(x + 4)}^{2}}{{(x - 4)}^{2}}$
$\frac{x^{2} - y^{2}}{x^{3} - y^{3}} \cdot \frac{x^{2} + x y + y^{2}}{x^{2} + 2 x y + y^{2}}$

Add and Subtract Rational Expressions

When rational expressions have the same denominator, we can add or subtract by adding or subtracting the numerators and retaining the common denominator. If the denominators differ, we must find equivalent rational expressions that have a common denominator. In general, it is most efficient to find the least common denominator (LCD) of the expressions.

To find the least common denominator of rational expressions, factor each denominator and form the product that uses each factor the greatest number of times it occurs in any factorization.

Example 1

Add.

$\begin{array}{l} \frac{x^{2} - 4 x + 4}{2 x^{2} - 3 x + 1} + \frac{x + 4}{2 x - 2} \\ \begin{array}{l} \begin{array}{l} = \frac{x^{2} - 4 x + 4}{(2 x - 1) (x - 1)} + \frac{x + 4}{2 (x - 1)} \\ The LCD is (2 x - 1) (x - 1) (2), or 2 (2 x - 1) (x - 1) . \\ = \frac{x^{2} - 4 x + 4}{(2 x - 1) (x - 1)} \cdot \frac{2}{2} + \frac{x + 4}{2 (x - 1)} \cdot \frac{2 x - 1}{2 x - 1} \\ = \frac{2 x^{2} - 8 x + 8}{(2 x - 1) (x - 1) (2)} + \frac{2 x^{2} + 7 x - 4}{2 (x - 1) (2 x - 1)} \\ = \frac{4 x^{2} - x + 4}{2 (2 x - 1) (x - 1)} \end{array} \end{array} \end{array}$

Example 2

Subtract.

$\begin{array}{l} \frac{x}{x^{2} + 11 x + 30} - \frac{5}{x^{2} + 9 x + 20} \\ \begin{array}{l} \begin{array}{l} = \frac{x}{(x + 5) (x + 6)} - \frac{5}{(x + 5) (x + 4)} \\ The LCD is (x + 5) (x + 6) (x + 4) . \\ = \frac{x}{(x + 5) (x + 6)} \cdot \frac{x + 4}{x + 4} - \frac{5}{(x + 5) (x + 4)} \cdot \frac{x + 6}{x + 6} \\ = \frac{x^{2} + 4 x}{(x + 5) (x + 6) (x + 4)} - \frac{5 x + 30}{(x + 5) (x + 4) (x + 6)} \\ = \frac{x^{2} + 4 x - (5 x + 30)}{(x + 5) (x + 6) (x + 4)} = \frac{x^{2} + 4 x - 5 x - 30}{(x + 5) (x + 6) (x + 4)} \\ = \frac{x^{2} - x - 30}{(x + 5) (x + 6) (x + 4)} = \frac{(x + 5) (x - 6)}{(x + 5) (x + 6) (x + 4)} \\ = \frac{(x - 6)}{(x + 6) (x + 4)} \end{array} \end{array} \end{array}$

Do Exercises 1–6.

Add or subtract and, if possible, simplify.

$\frac{a - 3 b}{a + b} + \frac{a + 5 b}{a + b}$
$\frac{x^{2} - 5}{3 x^{2} - 5 x - 2} + \frac{x + 1}{3 x - 6}$
$\frac{a^{2} + 1}{a^{2} - 1} - \frac{a - 1}{a + 1}$
$\frac{9 x + 2}{3 x^{2} - 2 x - 8} + \frac{7}{3 x^{2} + x - 4}$
$\frac{y}{y^{2} - y - 20} - \frac{2}{y + 4}$
$\frac{3 y}{y^{2} - 7 y + 10} - \frac{2 y}{y^{2} - 8 y + 15}$

Simplify Complex Rational Expressions

A complex rational expression has rational expressions in its numerator or its denominator or both.

To simplify a complex rational expression: First, add or subtract, if necessary, to get a single rational expression in the numerator and in the denominator. Then divide by multiplying by the reciprocal of the denominator.

Example

$\begin{array}{rcl} \frac{\frac{1}{a} + \frac{1}{b}}{\frac{1}{a^{3}} + \frac{1}{b^{3}}} & = & \frac{\frac{1}{a} \cdot \frac{b}{b} + \frac{1}{b} \cdot \frac{a}{a}}{\frac{1}{a^{3}} \cdot \frac{b^{3}}{b^{3}} + \frac{1}{b^{3}} \cdot \frac{a^{3}}{a^{3}}} \begin{array}{l} \begin{array}{l} \leftarrow The LCD is a b . \\ \leftarrow The LCD is a^{3} b^{3} . \end{array} \end{array} \\ = & \frac{\frac{b}{a b} + \frac{a}{a b}}{\frac{b^{3}}{a^{3} b^{3}} + \frac{a^{3}}{a^{3} b^{3}}} \\ = & \frac{\frac{b + a}{a b}}{\frac{b^{3} + a^{3}}{a^{3} b^{3}}} \\ = & \frac{b + a}{a b} \cdot \frac{a^{3} b^{3}}{b^{3} + a^{3}} \\ = & \frac{(b + a) (a) (b) (a^{2} b^{2})}{(a) (b) (b + a) (b^{2} - b a + a^{2})} \\ = & \frac{a^{2} b^{2}}{b^{2} - b a + a^{2}} \end{array}$

Do Exercises 1–5.

Simplify.

$\frac{\frac{x}{y} - \frac{y}{x}}{\frac{1}{y} + \frac{1}{x}}$
$\frac{\frac{a - b}{b}}{\frac{a^{2} - b^{2}}{a b}}$
$\frac{w + \frac{8}{w^{2}}}{1 + \frac{2}{w}}$
$\frac{\frac{x^{2} - y^{2}}{x y}}{\frac{x - y}{y}}$
$\frac{\frac{a}{b} - \frac{b}{a}}{\frac{1}{a} - \frac{1}{b}}$

Note: $b - a = - 1 (a - b)$ .

Simplify Radical Expressions

The symbol $\sqrt{a}$ denotes the nonnegative square root of a, and the symbol $\sqrt[3]{a}$ denotes the real-number cube root of a. The symbol $\sqrt[n]{a}$ denotes the nth root of a; that is, a number whose nth power is a. The symbol $\sqrt[n]{}$ is called a radical, and the expression under the radical is called the radicand. The number n (which is omitted when it is 2) is called the index.

Any real number has only one real-number odd root. Any positive number has two square roots, one positive and one negative. Similarly, for any even index, a positive number has two real-number roots. The positive root is called the principal root.

Examples

Simplify.

$\sqrt{36} = 6$ because $6 \cdot 6 = 36$ .
$- \sqrt{36} = - 6$
$\sqrt[3]{- 8} = - 2$
$\sqrt[5]{\frac{32}{243}} = \frac{2}{3}$
$\sqrt[4]{- 16} is not a real number$ .

Properties of Radicals

Let a and b be any real numbers or expressions for which the given roots exist. For any natural numbers m and $n (n \neq 1)$ :

If n is even, $\sqrt[n]{a^{n}} = | a |$ .
If n is odd, $\sqrt[n]{a^{n}} = a$ .
$\sqrt[n]{a} \cdot \sqrt[n]{b} = \sqrt[n]{a b}$ .
$\sqrt[n]{\frac{a}{b}} = \frac{\sqrt[n]{a}}{\sqrt[n]{b}} (b \neq 0)$ .
$\sqrt[n]{a^{m}} = {(\sqrt[n]{a})}^{m}$ .

Examples

Simplify.

$\sqrt{{(- 5)}^{2}} = | - 5 | = 5$
$\sqrt[3]{{(- 5)}^{3}} = - 5$
$\sqrt[4]{4} \cdot \sqrt[4]{5} = \sqrt[4]{4 \cdot 5} = \sqrt[4]{20}$
$\sqrt[3]{8^{5}} = {(\sqrt[3]{8})}^{5} = 2^{5} = 32$
$\sqrt{50} = \sqrt{25 \cdot 2} = \sqrt{25} \cdot \sqrt{2} = 5 \sqrt{2}$
$\frac{\sqrt{72}}{\sqrt{6}} = \sqrt{\frac{72}{6}} = \sqrt{12} = \sqrt{4 \cdot 3} = \sqrt{4} \cdot \sqrt{3} = 2 \sqrt{3}$
$\begin{array}{rcl} \sqrt{216 x^{5} y^{3}} & = & \sqrt{36 \cdot 6 \cdot x^{4} \cdot x \cdot y^{2} \cdot y} = \sqrt{36 x^{4} y^{2}} \sqrt{6 x y} \\ = & 6 x^{2} y \sqrt{6 x y} \end{array}$
$\begin{array}{rcl} 8 \sqrt{50} - 3 \sqrt{8} & = & 8 \sqrt{25 \cdot 2} - 3 \sqrt{4 \cdot 2} = 8 \cdot 5 \sqrt{2} - 3 \cdot 2 \sqrt{2} \\ = & 40 \sqrt{2} - 6 \sqrt{2} = 34 \sqrt{2} \end{array}$
$\begin{array}{rcl} (5 - \sqrt{2}) (4 + 3 \sqrt{2}) & = & 20 + 15 \sqrt{2} - 4 \sqrt{2} - 3 {(\sqrt{2})}^{2} \\ = & 20 + 11 \sqrt{2} - 6 = 14 + 11 \sqrt{2} \end{array}$

Do Exercises 1–20.

Simplify. Assume that no radicands were formed by raising negative quantities to even powers.

$\sqrt{{(- 21)}^{2}}$
$\sqrt{9 y^{2}}$
$\sqrt{{(a - 2)}^{2}}$
$\sqrt[3]{- 27 x^{3}}$
$\sqrt[4]{81 x^{8}}$
$\sqrt[5]{32}$
$\sqrt[4]{48 x^{6} y^{4}}$
$\sqrt{15} \sqrt{35}$
$\frac{\sqrt{40 x y}}{\sqrt{8 x}}$
$\frac{\sqrt[3]{3 x^{2}}}{\sqrt[3]{24 x^{5}}}$
$\sqrt{x^{2} - 4 x + 4}$
$\sqrt{2 x^{3} y} \sqrt{12 x y}$
$\sqrt{3 x^{2} y} \sqrt{36 x}$
$5 \sqrt{2} + 3 \sqrt{32}$
$7 \sqrt{12} - 2 \sqrt{3}$
$2 \sqrt{32} + 3 \sqrt{8} - 4 \sqrt{18}$
$6 \sqrt{20} - 4 \sqrt{45} + \sqrt{80}$
$(2 + \sqrt{3}) (5 + 2 \sqrt{3})$
$(\sqrt{8} + 2 \sqrt{5}) (\sqrt{8} - 2 \sqrt{5})$
${(1 + \sqrt{3})}^{2}$

Rationalizing Denominators

There are times when we need to remove the radicals in a denominator. This is called rationalizing the denominator. It is done by multiplying by 1 in such a way as to obtain a perfect nth power.

Examples

Rationalize the denominator.

$\sqrt{\frac{3}{2}} = \sqrt{\frac{3}{2} \cdot \frac{2}{2}} = \sqrt{\frac{6}{4}} = \frac{\sqrt{6}}{\sqrt{4}} = \frac{\sqrt{6}}{2}$
$\frac{2}{\sqrt{3}} = \frac{2}{\sqrt{3}} \cdot \frac{\sqrt{3}}{\sqrt{3}} = \frac{2 \sqrt{3}}{3}$
$\frac{\sqrt[3]{7}}{\sqrt[3]{9}} = \frac{\sqrt[3]{7}}{\sqrt[3]{9}} \cdot \frac{\sqrt[3]{3}}{\sqrt[3]{3}} = \frac{\sqrt[3]{21}}{\sqrt[3]{27}} = \frac{\sqrt[3]{21}}{3}$

Pairs of expressions of the form $a \sqrt{b}$ $+ c \sqrt{d}$ and $a \sqrt{b} - c \sqrt{d}$ are called conjugates. The product of such a pair contains no radicals and can be used to rationalize a denominator or a numerator.

Example 4

Rationalize the denominator: $\frac{7}{3 + \sqrt{5}}$ .

$\begin{array}{rcl} \frac{7}{3 + \sqrt{5}} & = & \frac{7}{3 + \sqrt{5}} \cdot \frac{3 - \sqrt{5}}{3 - \sqrt{5}} \\ = & \frac{21 - 7 \sqrt{5}}{3^{2} - 3 \sqrt{5} + 3 \sqrt{5} - {(\sqrt{5})}^{2}} \\ = & \frac{21 - 7 \sqrt{5}}{9 - 5} \\ = & \frac{21 - 7 \sqrt{5}}{4} \end{array}$

Do Exercises 1–7.

Rationalize the denominator.

$\frac{4}{\sqrt{11}}$
$\sqrt{\frac{3}{7}}$
$\frac{\sqrt[3]{7}}{\sqrt[3]{2}}$
$\sqrt[3]{\frac{16}{9}}$
$\frac{3}{\sqrt{30} - 4}$
$\frac{1 - \sqrt{2}}{\sqrt{3} - \sqrt{6}}$
$\frac{6}{\sqrt{m} - \sqrt{n}}$

Rational Exponents

For any real number a and any natural numbers m and n, $n \neq 1$ , for which $\sqrt[n]{a}$ exists:

$a^{1 / n} = \sqrt[n]{a}, a^{m / n} = {(\sqrt[n]{a})}^{m} = \sqrt[n]{a^{m}}, and a^{- m / n} = \frac{1}{a^{m / n}} .$

Examples

Convert to radical notation and, if possible, simplify.

$m^{1 / 6} = \sqrt[6]{m}$
$7^{3 / 4} = \sqrt[4]{7^{3}}$ , or ${(\sqrt[4]{7})}^{3}$
$8^{- 5 / 3} = \frac{1}{8^{5 / 3}} = \frac{1}{{(\sqrt[3]{8})}^{5}} = \frac{1}{2^{5}} = \frac{1}{32}$

Examples

Convert to exponential notation.

${(\sqrt[4]{7 x y})}^{5} = {(7 x y)}^{5 / 4}$
$\sqrt[6]{x^{3}} = x^{3 / 6} = x^{1 / 2}$

Examples

Simplify and then, if appropriate, write radical notation.

$\begin{array}{rcl} x^{5 / 6} \cdot x^{2 / 3} & = & x^{5 / 6 + 2 / 3} = x^{9 / 6} = x^{3 / 2} = \sqrt{x^{3}} \\ = & \sqrt{x^{2}} \sqrt{x} = x \sqrt{x} \end{array}$
${(x + 3)}^{5 / 2} {(x + 3)}^{- 1 / 2} = {(x + 3)}^{5 / 2 - 1 / 2} = {(x + 3)}^{2}$

Do Exercises 1–11.

Convert to radical notation and, if possible, simplify.

$y^{5 / 6}$
$x^{2 / 3}$
$16^{3 / 4}$
$4^{7 / 2}$
$125^{- 1 / 3}$
$32^{- 4 / 5}$

Convert to exponential notation.

$\sqrt[12]{y^{4}}$
$\sqrt{x^{5}}$

Simplify and then, if appropriate, write radical notation.

$x^{1 / 2} \cdot x^{2 / 3}$
${(a - 2)}^{9 / 4} {(a - 2)}^{- 1 / 4}$
${(m^{1 / 2} n^{5 / 2})}^{2 / 3}$

Pythagorean Theorem

A right triangle is a triangle with a 90° angle, as shown in the following figure. The small square in the corner indicates the 90° angle.

In a right triangle, the longest side is called the hypotenuse. It is also the side opposite the right angle. The other two sides are called legs. We generally use the letters a and b for the lengths of the legs and c for the length of the hypotenuse. They are related as follows.

The Pythagorean Theorem

In any right triangle, if a and b are the lengths of the legs and c is the length of the hypotenuse, then

$a^{2} + b^{2} = c^{2} .$

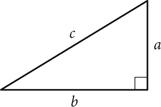
The equation $a^{2} + b^{2} = c^{2}$ is called the Pythagorean theorem.

Example 1

Find the length of the hypotenuse of this right triangle. Give an exact answer and an approximation to three decimal places.

$\begin{array}{rcl} 4^{2} + 5^{2} & = & c^{2} \\ 16 + 25 & = & c^{2} \\ 41 & = & c^{2} \\ c & = & \sqrt{41} \\ c & \approx & 6.403 \end{array}$

Example 2

Find the length of leg b of this right triangle. Give an exact answer and an approximation to three decimal places.

$\begin{array}{rcl} 10^{2} + b^{2} & = & 12^{2} \\ 100 + b^{2} & = & 144 \\ b^{2} & = & 144 - 100 \\ b^{2} & = & 44 \\ b & = & \sqrt{44} \\ b & \approx & 6.633 \end{array}$

Do Exercises 1–5.

Find the length of the third side of each right triangle. Where appropriate, give both an exact answer and an approximation to three decimal places.

..................Content has been hidden....................

You can't read the all page of ebook, please click here login for view all page.

Table of Contents for Just-In-Time Review

Create new playlist

Sign In

Sign Up

Table of Contents for
Just-In-Time Review