5.3 PDF of L-values for 2D Constellations
The analysis shown in Section 5.2 is slightly more involved in the case of 2D constellations. In what follows, we will first describe how to find the tessellation regions ![]() , and then, we will find the PDF of the L-values for arbitrary 2D constellations.
, and then, we will find the PDF of the L-values for arbitrary 2D constellations.
5.3.1 Space Tessellation
Finding the tessellation regions ![]() for 1D constellations is relatively simple and can be done by inspection, as we did, e.g., in Example 5.5. A more structured approach is required for 2D constellations, because as we will see, even with very regular constellations such as
for 1D constellations is relatively simple and can be done by inspection, as we did, e.g., in Example 5.5. A more structured approach is required for 2D constellations, because as we will see, even with very regular constellations such as ![]() QAM, the regions
QAM, the regions ![]() may significantly change in a function of the binary labeling.
may significantly change in a function of the binary labeling.
We start by rewriting (5.27) as

where ![]() ,
, ![]() , and
, and ![]() is given by (3.54).
is given by (3.54).
These tessellation regions ![]() are mutually disjoint
are mutually disjoint
and span the whole space
Moreover, because ![]() in (5.69) is defined by linear inequalities, the tessellation region may be (i) a (convex) polygon, (ii) a region that extends to infinity (i.e., an “infinite” polygon), or (iii) an empty set (if the inequalities in (5.69) are contradictory).
in (5.69) is defined by linear inequalities, the tessellation region may be (i) a (convex) polygon, (ii) a region that extends to infinity (i.e., an “infinite” polygon), or (iii) an empty set (if the inequalities in (5.69) are contradictory).
It should be rather clear that the regions ![]() cannot be deduced from the so-called Voronoi regions of the constellation (see (3.100)). The Voronoi regions depend solely on the constellation
cannot be deduced from the so-called Voronoi regions of the constellation (see (3.100)). The Voronoi regions depend solely on the constellation ![]() , while
, while ![]() depends also the on the labeling (via
depends also the on the labeling (via ![]() and
and ![]() ), or equivalently, on the subconstellations
), or equivalently, on the subconstellations ![]() and
and ![]() . However, the tessellation regions
. However, the tessellation regions ![]() can be obtained as the intersection of the Voronoi regions of the subconstellations
can be obtained as the intersection of the Voronoi regions of the subconstellations ![]() and
and ![]() , as explained in the following example.
, as explained in the following example.

Figure 5.13 Tessellation regions  in (5.69) for a 16QAM constellation labeled by the BRGC (see Fig. 2.14): (a)
in (5.69) for a 16QAM constellation labeled by the BRGC (see Fig. 2.14): (a)  , (b)
, (b)  , (c)
, (c)  , and (d)
, and (d)  . For clarity, only selected regions
. For clarity, only selected regions  are identified with labels. The subconstellations
are identified with labels. The subconstellations  and
and  are indicated by white and black circles, respectively
are indicated by white and black circles, respectively

Figure 5.14 Tessellation regions  , for an 8PSK constellation labeled by the BRGC. The subconstellations
, for an 8PSK constellation labeled by the BRGC. The subconstellations  and
and  are indicated by white and black circles, respectively
are indicated by white and black circles, respectively
Finding the tessellation regions in Examples 5.6 and 5.7 is relatively simple, however, this is not always the case. For example, when a 16PAM constellation labeled by the M16 (shown in Fig. 2.15) is considered, the labeling cannot be factorized as the ordered direct product of two labelings, so the tessellation regions are difficult to find by inspection. As we will see in Example 5.8, the regions in this case are very irregular, and thus, to find them, we require an algorithmic support.
In order to find ![]() , we need to remove redundant constraints from (5.69). The
, we need to remove redundant constraints from (5.69). The ![]() linear inequalities
linear inequalities ![]() and
and ![]() in (5.69) can be reformulated in a matrix form6 as
in (5.69) can be reformulated in a matrix form6 as
where
is an ![]() matrix,7 and where
matrix,7 and where ![]() and
and ![]() are
are ![]() matrices whose columns are taken from the respective sets
matrices whose columns are taken from the respective sets
Similarly, the ![]() vector
vector ![]() in (5.72) is
in (5.72) is
where ![]() and
and ![]() are
are ![]() column vectors whose elements are taken from the sets
column vectors whose elements are taken from the sets
respectively. To make (5.72) correspond to (5.69), we also assume that the matrix ![]() and the vector
and the vector ![]() are ordered in the same way. In other words, if the column of
are ordered in the same way. In other words, if the column of ![]() is defined by a particular pair of indices
is defined by a particular pair of indices ![]() , the same pair defines the corresponding element of
, the same pair defines the corresponding element of ![]() . The same applies to
. The same applies to ![]() and
and ![]() whose entries are defined by the pairs
whose entries are defined by the pairs ![]() .
.
In general, (5.72) has redundant inequalities, i.e., the number of linear forms defining the region ![]() is smaller than
is smaller than ![]() . Removing the redundant inequalities in (5.72) is a “classical” problem in computational geometry, and to solve it, we first require the region
. Removing the redundant inequalities in (5.72) is a “classical” problem in computational geometry, and to solve it, we first require the region ![]() to be closed, i.e., infinite polygons (which indeed exists, as shown in Fig. 5.13) are artificially closed by adding constraints forming a square with arbitrarily large dimensions
to be closed, i.e., infinite polygons (which indeed exists, as shown in Fig. 5.13) are artificially closed by adding constraints forming a square with arbitrarily large dimensions ![]()
where ![]() is a
is a ![]() vector of ones. We can keep track of these artificial constraints and, if they appear in the final solution, we should eliminate them, which would produce an infinite polygon. However, for practical purposes, retaining the artificial inequalities has negligible effect when
vector of ones. We can keep track of these artificial constraints and, if they appear in the final solution, we should eliminate them, which would produce an infinite polygon. However, for practical purposes, retaining the artificial inequalities has negligible effect when ![]() is sufficiently large.
is sufficiently large.
We then focus on the augmented problem
where ![]() is an
is an ![]() matrix and
matrix and ![]() is an
is an ![]() column vector. To solve (5.80), we translate the coordinates
column vector. To solve (5.80), we translate the coordinates ![]() via
via ![]() to obtain
to obtain
so that after the translation, ![]() satisfies all the inequalities in (5.82). The problem then boils down to finding a solution of
satisfies all the inequalities in (5.82). The problem then boils down to finding a solution of
Various methods may be used to find a feasible solution of the set of inequalities in (5.83). Here, we have solved the following quadratic optimization problem:
Note that the objective function ![]() is defined arbitrarily as we are interested in finding any translation point
is defined arbitrarily as we are interested in finding any translation point ![]() satisfying the constraints. If the solution of (5.84) does not exist, it means that the inequalities (5.72) are contradictory and the tessellation region
satisfying the constraints. If the solution of (5.84) does not exist, it means that the inequalities (5.72) are contradictory and the tessellation region ![]() is empty.
is empty.
After ![]() has been found, (5.82) can be expressed as
has been found, (5.82) can be expressed as
where ![]() . The next step is to normalize each inequality in (5.85) to obtain
. The next step is to normalize each inequality in (5.85) to obtain
where the normalization is such that the ![]() th row of
th row of ![]() is equal to the
is equal to the ![]() th row of
th row of ![]() divided by the (positive by definition)
divided by the (positive by definition) ![]() th entry of
th entry of ![]() .
.
The original problem in (5.72) expressed as in (5.86) is now in a standard form and can be solved using the duality between the line and points description. This duality states that removing redundant inequalities from (5.86) is equivalent to finding the minimum convex region enclosing the ![]() rows of
rows of ![]() , where each row is treated as a point in 2D space. We thus have to find a convex hull of these
, where each row is treated as a point in 2D space. We thus have to find a convex hull of these ![]() points, which can be done efficiently using numerical routines available, e.g., in MATLAB® or Mathematica®.
points, which can be done efficiently using numerical routines available, e.g., in MATLAB® or Mathematica®.
As we will see in the next section, to compute the PDF of the L-values, we need not only the linear pieces defining the tessellation regions ![]() but also the vertices of the polygons. Finding these vertices is again relatively simple and corresponds to a vertex enumeration problem treated in computational geometry.
but also the vertices of the polygons. Finding these vertices is again relatively simple and corresponds to a vertex enumeration problem treated in computational geometry.

Figure 5.15 Tessellation regions 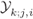 in (5.69) for a 16QAM constellation labeled by the M16: (see Fig. 2.15): (a)
in (5.69) for a 16QAM constellation labeled by the M16: (see Fig. 2.15): (a)  , (b)
, (b)  , (c)
, (c)  , and (d)
, and (d) 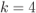 . For clarity, only selected regions
. For clarity, only selected regions  are identified with labels. The subconstellations
are identified with labels. The subconstellations  and
and  are indicated by white and black circles, respectively
are indicated by white and black circles, respectively
5.3.2 Finding the PDF
In the previous section, we have shown how to find the tessellation regions for arbitrary 2D constellations and labelings. The next step toward finding the PDF of the L-values is to find the CDFs ![]() as required by (5.31). We start by rewriting (5.69) as
as required by (5.31). We start by rewriting (5.69) as
where we use
to denote each of the ![]() nonredundant linear forms
nonredundant linear forms ![]() defining the tessellation regions
defining the tessellation regions ![]() , i.e., for each
, i.e., for each ![]() there exists a mapping between
there exists a mapping between ![]() and the indices
and the indices ![]() defining
defining ![]() . These nonredundant linear forms are the ones we have already shown, e.g., in Fig. 5.13: if
. These nonredundant linear forms are the ones we have already shown, e.g., in Fig. 5.13: if ![]() ,
, ![]() , and
, and ![]() , the region
, the region ![]() is an infinite polygon defined by
is an infinite polygon defined by ![]() linear forms; if
linear forms; if ![]() ,
, ![]() , and
, and ![]() , we obtain
, we obtain ![]() ; and for the region
; and for the region ![]() (the closed polygon containing
(the closed polygon containing ![]() and
and ![]() ), we have
), we have ![]() . We also define the vertices of the tessellation regions as
. We also define the vertices of the tessellation regions as ![]() .
.
The CDF ![]() (5.32) can be expressed as
(5.32) can be expressed as
where
contains observations ![]() which satisfy
which satisfy ![]() (this region is shown shaded in Fig. 5.16) and
(this region is shown shaded in Fig. 5.16) and
where ![]() given by (5.43). The equation
given by (5.43). The equation ![]() defines the line perpendicular to
defines the line perpendicular to ![]() , as schematically shown in Fig. 5.16.
, as schematically shown in Fig. 5.16.

Figure 5.16 The tessellation region  is a polygon delimited by the lines
is a polygon delimited by the lines  , where
, where 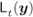 is given by (5.88). The values of
is given by (5.88). The values of  defining the intervals
defining the intervals  in (5.93) for
in (5.93) for  together with the line
together with the line  and the two active linear pieces are also shown. The shaded area corresponds to
and the two active linear pieces are also shown. The shaded area corresponds to 
The region ![]() in (5.90) is a subset of (5.87) and depends on
in (5.90) is a subset of (5.87) and depends on ![]() . Further, to simplify the presentation, we assume that the tessellation region
. Further, to simplify the presentation, we assume that the tessellation region ![]() is a closed polygon defined by
is a closed polygon defined by ![]() nonredundant inequalities. Then the line
nonredundant inequalities. Then the line ![]() either (i) intersects8 two sides of polygon
either (i) intersects8 two sides of polygon ![]() and these sides are then active, or (ii) does not have a common point with the polygon. The first case is critical to the calculation of the CDF. We note that while the indices of the linear forms
and these sides are then active, or (ii) does not have a common point with the polygon. The first case is critical to the calculation of the CDF. We note that while the indices of the linear forms ![]() defining the active sides change with
defining the active sides change with ![]() , they remain constant as long as, varying
, they remain constant as long as, varying ![]() , the line
, the line ![]() does not cross one of the vertices
does not cross one of the vertices ![]() of the polygon; i.e., the indices change when
of the polygon; i.e., the indices change when ![]() satisfies
satisfies ![]() , which may occur for
, which may occur for ![]() distinct values of
distinct values of ![]() defined by
defined by
Thus, denoting by ![]() the sorted values of
the sorted values of ![]() in (5.92), we find the
in (5.92), we find the ![]() intervals
intervals
such that
For a given value of ![]() , we will use the indices
, we will use the indices ![]() and
and ![]() to denote the two sides of the polygon which remain active for all
to denote the two sides of the polygon which remain active for all ![]() .
.
To clarify the above discussion, consider the example shown in Fig. 5.16. In this case, we have ![]() and
and ![]() ,
, ![]() , and
, and ![]() . For the particular value of
. For the particular value of ![]() in Fig. 5.16,
in Fig. 5.16, ![]() so
so ![]() and
and ![]() . Furthermore, in this figure we schematically show the values of
. Furthermore, in this figure we schematically show the values of ![]() as a projection of the vertices on the line connecting
as a projection of the vertices on the line connecting ![]() and
and ![]() which becomes the “axis” for the arguments
which becomes the “axis” for the arguments ![]() of the PDF (see also Fig. 3.2). The origin of this axis corresponds to
of the PDF (see also Fig. 3.2). The origin of this axis corresponds to ![]() . Note that the origin does not necessarily belong to
. Note that the origin does not necessarily belong to ![]() .
.
The calculation of (5.89) requires now a 2D-equivalent of the integration shown in (5.48). This is practically the same problem we need to solve when evaluating the bit- and symbol-error rates, so the approach we have adopted here is also explained in detail in Section 6.1.2. More particularly, we decompose the observation space ![]() into elementary wedges (see also (6.34)) defined as
into elementary wedges (see also (6.34)) defined as
Integration over such wedge can be expressed as9
where ![]() is the bivariate Q-function defined in (2.11).
is the bivariate Q-function defined in (2.11).
As shown in Fig. 5.16, the union of the wedges and the polygon over which the integration must be carried out yields the entire observation space. In the particular case shown in Fig. 5.16 we can write
where we used shorthand notation ![]() to denote the parameters of the linear form (5.91). We note that the linear form
to denote the parameters of the linear form (5.91). We note that the linear form ![]() , being redundant for the definition of
, being redundant for the definition of ![]() (for the particular value of
(for the particular value of ![]() used in this example), does not affect the integration result.
used in this example), does not affect the integration result.
We are now ready to find the conditional PDF of the L-values ![]() .
.
Analyzing Theorem 5.10, we note that the indicator function in (5.106) takes into account the variation of the indices ![]() and
and ![]() because of the change of
because of the change of ![]() moving throughout the intervals
moving throughout the intervals ![]() . As we see, the form of the PDF does not depend uniquely on
. As we see, the form of the PDF does not depend uniquely on ![]() ,
, ![]() , and
, and ![]() , but also on other symbols from the constellation which define the polygon's sides. We also note that the Gaussian piece
, but also on other symbols from the constellation which define the polygon's sides. We also note that the Gaussian piece ![]() we have already obtained in the case of 1D constellations, is still present, but it is now multiplied by the “correction” terms (5.107).
we have already obtained in the case of 1D constellations, is still present, but it is now multiplied by the “correction” terms (5.107).
5.3.3 Case Study: 8PSK Labeled by the BRGC
In this section, we consider an 8PSK constellation, which is probably the simplest nontrivial example of a 2D constellation. Furthermore, because of its practical relevance, we consider the BRGC. The constellation and labeling are shown in Fig. 5.14.
The tessellation regions are simple to find as we have already shown it in Example 5.7: they are always either (i) the Voronoi regions of the constellation symbols (e.g., ![]() ,
, ![]() in Fig. 5.14) or (ii) a union of two Voronoi regions (e.g.,
in Fig. 5.14) or (ii) a union of two Voronoi regions (e.g., ![]() , or any
, or any ![]() , see again Fig. 5.14). This property spares us the need to apply the algorithmic approach of Section 5.3.1, which means we do not need to set the artificial constraints (5.79). Second, because of symmetry of the BRGC, the regions also have a notable symmetry, which we will exploit to simplify the analysis.
, see again Fig. 5.14). This property spares us the need to apply the algorithmic approach of Section 5.3.1, which means we do not need to set the artificial constraints (5.79). Second, because of symmetry of the BRGC, the regions also have a notable symmetry, which we will exploit to simplify the analysis.
As for ![]() PSK constellations
PSK constellations ![]()
![]() , we obtain
, we obtain
and thus,
The expression in (5.112) shows that all the lines delimiting the regions pass through the origin and so does the line ![]() .
.
Let us focus on the case ![]() which also gives us the results for
which also gives us the results for ![]() (as explained in Example 5.7). This case is shown in Fig. 5.17. The piece of the PDF
(as explained in Example 5.7). This case is shown in Fig. 5.17. The piece of the PDF ![]() depends on the form of the tessellation region
depends on the form of the tessellation region ![]() as well as on the position of the symbol
as well as on the position of the symbol ![]() with respect to this region. An inspection of the constellation in Fig. 5.17 lets us conclude the following:
with respect to this region. An inspection of the constellation in Fig. 5.17 lets us conclude the following:

Figure 5.17 Some tessellation regions for 8PSK labeled by the BRGC and  . To obtain
. To obtain  ,
,  ,
,  , or
, or  for
for  , integration should be carried over the shaded regions
, integration should be carried over the shaded regions
- Because of the symmetry of the constellation and the tessellation regions, we may write
5.114
 5.115
5.115
thus, it is sufficient to find
 for
for 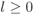 , conditioned on
, conditioned on 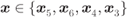 .
. - For
 the lines
the lines  always intersect with the same sides of the tessellation regions, therefore we do not need to take into account intervals changing with
always intersect with the same sides of the tessellation regions, therefore we do not need to take into account intervals changing with  as in (5.106). This is obvious from Fig. 5.17: the line
as in (5.106). This is obvious from Fig. 5.17: the line  crosses the same two sides of the region
crosses the same two sides of the region  , the line
, the line 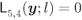 crosses only one side of
crosses only one side of  , and so on. Considering only
, and so on. Considering only  thus simplifies the analysis.
thus simplifies the analysis. - Inspecting the regions
 and
and  (shown shaded), we conclude that
(shown shaded), we conclude that

i.e.,
 .Moreover, for
.Moreover, for  we observe the following relationship:
we observe the following relationship:
i.e.,
 .
.
After differentiation and generalization to other regions we obtain the following relationships:
The advantage of (5.116)–(5.118) is that we can now express the PDF ![]() using (5.33) as
using (5.33) as
The same can be done for the PDF pieces conditioned on ![]() , namely,
, namely,
which yields
Thus, instead of varying the regions ![]() for a constant
for a constant ![]() as suggested by (5.33), in (5.120) and (5.125), we limit our considerations to two regions
as suggested by (5.33), in (5.120) and (5.125), we limit our considerations to two regions ![]() and change the symbols
and change the symbols ![]() . We emphasize that this is possible in the particular case of an
. We emphasize that this is possible in the particular case of an ![]() PSK constellation labeled by the BRGC because of the symmetries of the constellation and the binary labeling. This is very convenient because we only need to find
PSK constellation labeled by the BRGC because of the symmetries of the constellation and the binary labeling. This is very convenient because we only need to find ![]() and
and ![]() for
for ![]() .
.
The same can be done for ![]() . In this case, only one symbol needs to be considered, namely,
. In this case, only one symbol needs to be considered, namely, ![]() . It can be shown that in this case
. It can be shown that in this case
In order to reuse the results obtained for ![]() , we can further exploit the equivalence (up to a rotation) of the tessellation regions
, we can further exploit the equivalence (up to a rotation) of the tessellation regions ![]() and
and ![]() (see Fig. 5.13), i.e.,
(see Fig. 5.13), i.e., ![]() for
for ![]() and
and ![]() .
.
Up to now, we have shown the PDF ![]() can be expressed as a function of
can be expressed as a function of ![]() and
and ![]() . The next step is to use Theorem 5.10. Before doing this, however, we study some properties of
. The next step is to use Theorem 5.10. Before doing this, however, we study some properties of ![]() PSK constellations.
PSK constellations.
More specifically, using ![]() , where
, where ![]() (see (2.52)), we find
(see (2.52)), we find
where
Similarly, we can find
We can now analyze the contribution of the region ![]() . From (5.106), we obtain
. From (5.106), we obtain
where ![]() , and
, and ![]() . Here,
. Here, ![]() ,
, ![]() and
and ![]() , so (5.107) becomes
, so (5.107) becomes
where we used ![]() .
.
Note that there is only one correction term ![]() in (5.136) because the region
in (5.136) because the region ![]() is a semi-infinite polygon and the line
is a semi-infinite polygon and the line ![]() intersects only one of its sides. Equivalently, we might set an artificial constraint to close the polygon, e.g.,
intersects only one of its sides. Equivalently, we might set an artificial constraint to close the polygon, e.g., ![]() , where
, where ![]() and
and ![]() . Then
. Then ![]() and
and ![]() , cf. (5.107).
, cf. (5.107).
Similarly, for ![]() we obtain
we obtain
where ![]() ,
, ![]() , and
, and ![]() and
and ![]() , so
, so
with ![]() , and
, and ![]() .
.
The form of ![]() is shown in Fig. 5.18 for
is shown in Fig. 5.18 for ![]() and
and ![]() , where we identify the pieces
, where we identify the pieces ![]() . Similarly, we show the corresponding results for
. Similarly, we show the corresponding results for ![]() in Fig. 5.19. We can observe that for
in Fig. 5.19. We can observe that for ![]() , the term
, the term ![]() has a “dominating” contribution to
has a “dominating” contribution to ![]() . In particular, in Fig. 5.18 (a), we see that for
. In particular, in Fig. 5.18 (a), we see that for ![]() ,
, ![]() takes on the largest values, while in Fig. 5.18 (b), we see that for
takes on the largest values, while in Fig. 5.18 (b), we see that for ![]() , the piece
, the piece ![]() dominates the others. Finally, in Fig. 5.19 we see that for
dominates the others. Finally, in Fig. 5.19 we see that for ![]() ,
, ![]() is again the dominating piece.
is again the dominating piece.

Figure 5.18 PDF of the L-values for an 8PSK constellation labeled by the BRGC and 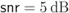 :
:  (thick solid lines) in (5.120) and the pieces
(thick solid lines) in (5.120) and the pieces  (lines with markers) for (a)
(lines with markers) for (a)  and (b)
and (b) 

Figure 5.19 PDF of the L-values for an 8PSK constellation labeled by the BRGC and  :
:  (thick solid line) in (5.120) and the pieces
(thick solid line) in (5.120) and the pieces  (lines with markers)
(lines with markers)

