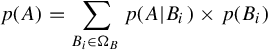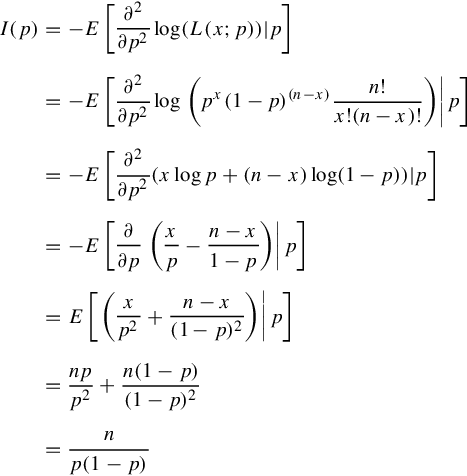3.1 A Multidisciplinary Background

The inspiration for developing mathematical foundations for reliability of social sensing systems comes from multiple research communities. Many of these communities do not interact. They have different research objectives, different applications, and different publication venues. As a result, some opportunities were missed for connecting the dots between their advances. Jointly, these advances offer the needed foundations for leveraging unreliable social sensing sources, while offering collective reliability guarantees.

In the sensor fusion community, well established results exist that describe estimation algorithms using noisy sensors and quantify the corresponding estimation error bounds. It is possible to exploit Bayesian analysis to combine evidence and use estimation theory to rigorously compute confidence intervals as a function of reliability of input sources, even in the presence of noise and uncertainty. These results have typically been applied to the estimation of physical signals and tracking dynamic state such as trajectories of mobile targets. Given a physical model of how a target behaves, and given some observations, theory was developed on how to infer hidden variables that are not directly observed. Since sensor fusion deals with measuring state of the physical world, a key concept that threads through the research is the existence of a unique ground truth (barring, for the moment, the quantum effects and Schrodinger’s cat). The existence of a unique ground truth offers a non-ambiguous notion of error that quantifies the deviation of estimated state from ground truth. In turn, the existence of a non-ambiguous notion of error lends itself nicely to the formulation of optimization problems that minimize this error. Such problems were formulated for estimating the state of physical systems, usually given by well-understood models, from noisy indirect observations. However, they have seldom been applied to the estimation of parameters of social sources and reliability of social observations.

Data mining researchers, on the other hand, do not usually exploit physical models of targets. This is because of the nature of the data mining problems. Rather than dealing with well-defined and well-understood objects for which physical dynamic models exist, data mining research tries to understand very large systems, and infer relations that are observed to hold true in the data. Much advances were made in data mining on representing very large data sets as abstract graphs of heterogeneous nodes, and inferring interesting new properties of the underlying systems from the topology of such graphs. This area is referred to as heterogeneous network mining. The analysis techniques described in that space are mostly heuristic, but have the power of producing interesting insights starting with no prior knowledge about the system whose data are collected. Importantly, since the system in question is often very complex and not well-understood, much of the work stops at computing different properties, without defining a notion of error. In many cases, ground truth cannot be defined. For example, when clustering individuals according to their beliefs into liberals and conservatives, it is really hard to define a rigorous and unbiased notion of what ground truth means, and offer a non-ambiguous notion of error. As a consequence of the difficulty in defining error for solutions of data mining problems, few problems are cast as ones of error optimization. Rather, data mining problems are often cast as minimizing internal conflict between observations. Hence, data mining literature does not usually offer bounds on error of data mining algorithms.

Machine learning researchers take a different approach to extracting properties of poorly understood systems. They typically propose a generative model for how the system behaves. Unlike researchers in sensor data fusion who often exploit representations of the exact dynamics of their targets, in machine learning the generative model has hidden parameters that are estimated only empirically. Machine learning literature describes techniques for learning model parameters using algorithms such as expectation maximization (EM).

The above body of results, put together, suggests an approach to reliable social sensing. Namely, we borrow from data mining the techniques used for knowledge representation. Specifically, we represent sources and observations by graphs that allow us to infer interesting properties of nodes. We then borrow from machine learning the idea of using generative models with hidden parameters to be estimated. Hence, we propose simple models for behavior of individual nodes in those graphs, such as lying, gossiping, or telling the truth. These models allow us to compute likelihood of observations as a function of model parameters of nodes. Finally, once a generative model is present, we are able to use the body of results developed in sensor data fusion to design optimal estimators and assess estimator error and confidence intervals. Specifically, we find model parameters that maximize the likelihood of the specific graph topology borne out from our data. Note specifically that, since the final outcome of this work is to decide which of a large number of social observations are true, we are able to define a rigorous notion of ground truth. After all, the observations we are interested in are those concerning the physical state of the world. Hence, ground truth exists (although is not known). A non-ambiguous notion of error therefore exists as well, and we are able to rigorously cast reliable social sensing as an error optimization problem.

Below, we first survey the foundations of social sensing borrowed from aforementioned different communities. We then bring it all together and discuss our problem formulation.

3.2 Basics of Generic Networks

A generic network represents an abstraction of our real world with a focus on the objects (normally represented by nodes) and the interactions between the objects (normally represented by links) [80]. Our world is an interconnected world. A large number of information and physical entities (e.g., individual agents, social groups, web pages, genomes, vehicles, computers, etc.) are interconnected or interact with each other and form numerous, large-scale, and sophisticated networks. Some well-known examples of generic networks include World Wide Web, social networks, biological networks, transportation networks, epidemic networks, communication networks, healthcare networks, electrical power grids, and so on. Due to its prevalence and importance, the analysis of generic networks has gained a wide attention from researchers from different disciplines (e.g., computer science, sociology, biology, physics, economics, health, and so on).

Considering the node and link types, generic networks in general can be classified into two main categories: homogeneous and heterogeneous. Homogeneous networks usually represent the networks where the nodes are the objects of the same type and links are the relationships from the same type. A popular example of such networks is the web page network, which is the fundamental abstraction of Google’s PageRank algorithm [34]. In this network, entities are all of the same type (i.e., web pages) while links are also of the same type (i.e., hyperlinks). In contrast, heterogeneous networks are the networks where the nodes and links are of different types. For example, in a university network, we may have different types of nodes to represent professors, students, courses, and departments as well as different types of links to represent their interactions such as teaching, course registration, or departmental association. Hence, we need to treat different nodes and links in heterogeneous networks as appropriate types to better capture the essential semantics of the real world [81].

Numerous techniques and methods have been developed to analyze both homogeneous [82–85] and heterogeneous [36, 86–88] networks. Many homogeneous network problems are related with World Wide Web and social networks. Examples include ranking [82], community detection [83], link prediction [84], and influence analysis [85]. State-of-the-art research developments in heterogeneous networks explore the power of links to mine hidden information related with both nodes and links in the network. Examples include fact-finding [36], rank-based clustering [86], relationship prediction [87], and network evolution [88]. In this chapter, we focus on a special type of heterogeneous networks that are usually used in fact-finding literature [35–37] and relate that to the data reliability problem in social sensing. In its simplest form, this special type of heterogeneous networks can be represented by bipartite graphs. Nodes on one side of the graph represent information sources and nodes on the other side represent information entities. The links in the graph connecting two types of nodes describe which source contributes/claims which information entity. The goal of the problem is to find the attributes of the nodes in the graph. For example, what is the likelihood of a source to generate a correct information entity? What is the probability of a given entity to be true? This bipartite graph can be generated to model more complex networks where links between sources and links between information entities are considered.

In the rest of this chapter, we will first review several basic concepts and methods from statistics and estimation theory that will be used throughout this book. They include Bayesian analysis in Section 3.3, maximum likelihood estimation (MLE) in Section 3.4, EM in Section 3.5 and confidence intervals in Section 3.6. Then we will put everything together under a framework that studies the aforementioned heterogeneous network in Section 3.7.

3.3 Basics of Bayesian Analysis

Bayesian analysis (also called Bayesian inference or Bayesian statistics) is a method of analysis where the Bayes’ rule is used to update the probability estimate of a hypothesis as additional data is observed [89]. In this section, we review the basics of Bayesian analysis. Let us start with a simple example. Suppose a 50-year-old patient has a positive lab test for a cardiac disease. Assume the accuracy of this test is 95%. That is to say given a patient has a cardiac disease, the probability of positive result of this test is 95%. In this scenario, the patient would like to know the probability that he/she has the cardiac disease given the positive test. However, the information available is the probability of testing positive if the patient has a cardiac disease, along with the fact that the patient had a positive test result.

Bayes’ theorem offers a way for us to answer the above question. The basic theorem simply states:

$\begin{array}{l}\hfill p(B|A)=\frac{p(A|B)\times p(B)}{p(A)}\end{array}$

where event B represents the event of our interests (e.g., having a cardiac disease) and A represents an event related to B (e.g., positive lab test). p(B|A) is the probability of event B given event A, p(A) and p(B) is the unconditional marginal probability of event A and B, respectively. The proof of Bayes’ theorem is straightforward: we know from probability rules that p(A,B) = p(A|B) × p(B) and p(B,A) = p(B|A) × p(A). Given the fact that p(A,B) = p(B,A), we can easily obtain:

$\begin{array}{l}\hfill p(A|B)\times p(B)=p(B|A)\times p(A)\end{array}$

Then we divide each side by p(A), we obtain Equation (3.1). Normally, p(A|B) is given in the context of applications (e.g., the lab test accuracy in our example) and p(B|A) is what we are interested to know (e.g., the probability of having a cardiac disease given a positive lab test result). p(B) is the unconditional probability of the event of interests, which is usually assumed to be known as prior knowledge (e.g., the probability of a 50-year-old to have a cardiac disease in the population). p(A) is the marginal probability of A, which can be computed as the sum of the conditional probability of A under all possible events of B in its sample space Ω_B. In our example, the sample space of B is whether a patient has a cardiac disease or not. Formally, p(A) can be computed as:

$\begin{array}{l}\hfill p(A)=\sum _{B_i\in {\mathrm{\Omega }}_B}p(A|B_i)\times p(B_i)\end{array}$

Now, let us come back to our cardiac disease example to make the theorem more concrete. Suppose that, in addition to the 95% accuracy of the test, we also know the false positive rate of the lab test is 40%, which means the test will produce the positive results with a probability of 40% given the patient does not have the cardiac disease. Hence, we have two possible events for B: B₁ represents the event that the patient has the cardiac disease while B₂ represents the negation. Given the accuracy and false positive rate of the test, we know p(A|B₁) = 0.95 and p(A|B₂) = 0.4. The prior knowledge p(B) is the marginal probability of a patient to have a cardiac disease, not knowing anything beyond the fact he/she is a 50-year-old. We call this information prior knowledge because it exists before the test. Suppose we know from previous research and statistics that the probability of a 50-year-old to have a cardiac disease is 5% in the population. Using all above information, we can compute p(B|A) as follows:

$\begin{array}{l}\hfill p(B|A)=\frac{0.95\times 0.05}{0.95\times 0.05+0.4\times 0.95}=\frac{0.0475}{0.0475+0.38}=0.111\end{array}$

Therefore, the probability of a patient to have a cardiac disease given the positive test is only 0.111. In Bayesian theorem, we call such probability the posterior probability, because it is the estimated probability after we observe the data (i.e., the positive test result). The small posterior probability is somewhat counter-intuitive given a test with so-called “95%” accuracy. However, if we look at the Bayes’ theorem, a few factors affect this probability. First is the relatively low probability to have the cardiac disease (i.e., 5%). Second is the relatively high false positive rate (i.e., 40%), which will be further enlarged by the high probability of not having a cardiac disease (i.e., 95%).

The next interesting question to ask is: what happens to Bayes theorem if we have more data. Suppose that, in the first experiment, we have data A₁. After that we repeat the experiment and have new data A₂. Let us assume that A₁ and A₂ are conditionally independent. We want to compute the posterior probability of B after two experiments: p(B|A₁,A₂). This can be done using the basic Bayes’ theorem in Equation (3.1) as follows:

$\begin{array}{ll}\hfill p(B|A_1,A_2)& =\frac{p(A_1,A_2|B)\times p(B)}{p(A_1,A_2)}\hfill \\ \hfill & =\frac{p(A_1|B)\times p(A_2|B)\times p(B)}{p(A_1)\times p(A_2|A_1)}\hfill \\ \hfill & =\frac{p(B|A_1)\times p(A_2|B)}{p(A_2|A_1)}\hfill \end{array}$

The above result tells us we can use the posterior of the first experiment (i.e., p(B|A₁)) as the prior for the second experiment. The process of repeating the experiment and recomputing the posterior probability of interest is the basic process in Bayes’ analysis. From a Bayesian perspective, we start with some initial prior probability of some event of interests. Then we keep on updating this prior probability with a posterior probability that is computed using the new information we obtained from experiment. In practice, we continue to collect data to examine a particular hypothesis. We do not start each time from scratch by ignoring all previously collected data. Instead, we use our previous analysis results as prior knowledge for the new experiment to examine the hypothesis.

Let us come back to our cardiac example again. Once the patient knows the limitation of the test, he/she may choose to repeat the test. Now the patient can use Equation (3.5) to compute the new p(B) after each repeated experiment. For example, if the patient repeats the test one more time, the new posterior probability of having a cardiac disease is:

$\begin{array}{l}\hfill p(B|A)=\frac{0.95\times 0.111}{0.95\times 0.111+0.4\times 0.889}=\frac{0.10545}{0.10545+0.3556}=0.229\end{array}$

This result is still not very affirmative to claim the patient has a cardiac disease. However, if the patient chooses to keep on repeating the test and finding positive results, his/her probability to have a cardiac disease increases. In the following repeated test, subsequent positive results generate probabilities: test 3 = 0.41352, test 4 = 0.62611, test 5 = 0.79908, test 6 = 0.90427, test 7 = 0.95733, test 8 = 0.98158, test 9 = 0.99216, test 10 =0.99668. As we can see, after enough tests and successive positive test results, the probability to make an affirmative conclusion is pretty high. Note that the above is a toy example to demonstrate the basic Bayesian analysis. It assumes that the results of all tests are statically independent conditioned on B, which may not always be true in actual medical tests.

3.4 Basics of Maximum Likelihood Estimation

In statistics and estimation theory, MLE is a method to estimate the parameters of a statistical model in a way that is asymptotically most consistent with the data observed. Let us start with a simple example to explain the intuition of this method. In this example, we have a random number generator G(T). It can generate a random integer number from 1 to T with a uniform probability distribution (i.e., it has the same probability to generate every number in its range). Let us first suppose that T only has two possible values: 10 and 20. After one run, the generator generated a number: 5. The question is: which of the two values does T equal to? Many people guess T is 10. Their reason is that 5 is more likely to come up when T is 10 (i.e., the probability is 0.1) than T is 20 (i.e., the probability is 0.05). Now suppose T can be any integer value, the generated number is still 5. What is the most likely value of T? I guess you already get the answer: 5. The reason is simple: in the case T < 5: the probability to generate 5 is 0; in the case T > 5: the probability to generate 5 is smaller than the case of T = 5. The above reasoning follows the basic principle of MLE: make the guess of estimated parameters for which the observed data are least surprising.

In general, for a fixed set of data and given statistical model, the MLE method searches for the set of values of the model parameters that maximize the likelihood of the selected model matching the observed data. Formally, suppose X₁,X₂,…,X_n are statistically independent random variables with a family of distributions represented by f(X_i|θ), where θ is the unknown vector of estimation parameters that determines the distribution. For continuous random variables, f(X_i|θ) represents the probability density function of X_i. For discrete variables, f(X_i|θ) represents the probability mass function (pmf) p(X_i|θ). To use the MLE method, one first need to specify the joint density function of all observations. Let us denote the observed values X₁ = x₁,…,X_n = x_n. The joint density function is:

$\begin{array}{l}\hfill f(x_1,x_2,\dots ,x_n|\theta )=f(x_1|\theta )\times f(x_2|\theta )\times \cdots \times f(x_n|\theta )\end{array}$

The above joint density function can be seen from a different perspective. One can consider x₁,x₂,…,x_n as the fixed “parameters” of the above function and consider θ as the “variable” of the function that can change freely. Then we can rewrite the above function as follows:

$\begin{array}{l}\hfill L_n(\theta ;x_1,x_2,\dots ,x_n)=f(x_1|\theta )\times f(x_2|\theta )\times \cdots \times f(x_n|\theta )=\prod _{i=1}^{n}f(x_i|\theta )\end{array}$

The above function is called the likelihood function. It represents the joint probability of observing the data values X₁ = x₁,…,X_n = x_n as a function of the parameter θ. The MLE $\widehat{{\theta }_n}$ is the estimated value of θ that maximizes the likelihood function (i.e., $L(\widehat{{\theta }_n})\ge L(\theta )$ for all θ). Since it is easier to deal with sums than products, we usually use the logarithm of the likelihood function in practice. We call this function log-likelihood function:

$\begin{array}{l}\hfill ln{L}_n(\theta ;x_1,x_2,\dots ,x_n)=\sum _{i=1}^{n}lnf(x_i|\theta )\end{array}$

The derivation of the log-likelihood function is called score function:

$\begin{array}{l}\hfill V_n(\theta )=\frac{\partial }{\partial \theta }ln{L}_n(\theta ;x_1,x_2,\dots ,x_n)=\sum _{i=1}^n\frac{\partial }{\partial \theta }lnf(x_i|\theta )\end{array}$

Usually we can find the MLE by setting the score function to 0 (i.e., V_n(θ) = 0 for $\widehat{{\theta }_n})$). V_n(θ) is a random function of θ and the solution $\widehat{{\theta }_n}$ is a random variable.

Now let us review the basic concepts and ideas of MLE by walking through a simple example. In this example, we consider the following binomial distribution:

$\begin{array}{l}\hfill P(x|n,p)=\left(\genfrac{}{}{0.0pt}{}{n}{x}\right)p^x{(1-p)}^{(n-x)}\end{array}$

where P(x|n,p) represents the probability of x successes in a sequence of n Bernoulli experiments, each of which yields success with probability p. For example, suppose p = 0.7 and n = 10, we can use the above equation to answer the question: “what is the probability to have 4 successful experiments in 10 trials?” However, we can look at the problem from a different perspective: suppose we do not know the value of p before the experiments, but after 10 trials, we know that there are 4 successful experiments. Then our question is: “what is the most likely value of p?” This is a MLE problem: now the data x are fixed, we view Equation (3.11) as a function of parameter p, and use it to compute the MLE of p. Thus we define the likelihood function of our problem as:

$\begin{array}{l}\hfill L(p|n,x)=\left(\genfrac{}{}{0.0pt}{}{n}{x}\right)p^x{(1-p)}^{(n-x)}\end{array}$

which is essentially the same function as Equation (3.11), but it is now viewed as a function of p. The MLE of p is the value of p that maximizes the function L(p|n,x). It is easier to maximize the logarithm of the likelihood function, which is:

$\begin{array}{l}\hfill logL(p|n,x)=log\left(\genfrac{}{}{0.0pt}{}{n}{x}\right)+xlogp+(n-x)log(1-p)\end{array}$

We set the derivative of the above function to 0 with respect to p, and solve for p the value that maximize the likelihood function. It turns out that in this case, the MLE of p is $\widehat{p}=\frac{x}{n}$, which matches with our intuition.

The negative second derivative of the likelihood function is called observed information I(θ), which is defined as follows:

$\begin{array}{l}\hfill I_n(\theta )=-\frac{{\partial }^2}{\partial {\theta }^2}ln{L}_n(\theta )=-\sum _{i=1}^n\frac{{\partial }^2}{\partial {\theta }^2}lnf(x_i|\theta )=\frac{\partial }{\partial \theta }{V}_n(\theta )\end{array}$

The observed information in general depends on the observe data, and is also a random variable. The Fisher information is defined as the expectation of the observed information, which is a way of measuring the amount of information the observed random variable X carries about the unknown estimation parameter θ upon which the probability of X depends. It can be proved that expected value of the score function V_n(θ) is 0 and the variance of V_n(θ) is the Fisher information at θ [90]. Also the fisher information and score function can be used in a recursive method to estimate the model parameters efficiently [91].

The MLE has several nice properties. The first one is called consistent: $\widehat{\theta }$ converges to the true value of θ (i.e., θ₀) both in weak and strong convergence. The second one is called asymptotic normality: as the sample size n increases, the distribution of MLE tends to be the Gaussian distribution with mean as θ₀ and covariance matrix equals to the inverse of the Fisher information matrix. The third one is called efficiency: as the sample size goes to infinity, the MLE achieves the least mean squared error among all consistent estimators. Its performance can be characterized by Cramer-Rao lower bound (CRLB), which will be discussed in details in Section 3.6. For the proofs of the above properties, one can refer to [92] for details.

3.5 Basics of Expectation Maximization

In statistics and estimation theory, EM is an iterative algorithm that is used to find the maximum likelihood or maximum posteriori estimation of parameters of statistical models, where the data are “incomplete” or the likelihood function involves latent variables [93]. The latent variables (sometimes also called hidden variables) are defined as the variables that are not directly observed from the data we have but can rather be inferred from the observed variables. Here is a simple example of Binomial Mixture Model: we have two binary number generators which generate either 1 or 0 in a trial. Suppose the probability of generating 1s of two generators are p₁,p₂, respectively. Every trial we choose the first generator with probability q and the second one with probability 1 − q. Suppose that, we used the two generators to generate a sequence of binary numbers x = 1,0,0,1,0,1,1,0,1,1,1,0. Our goal here is to jointly estimate θ = (p₁,p₂,q) from the data we observed (i.e., x). This problem is a bit tricky because we do not know which generator was used in every trial to generate numbers and p₁,p₂ can be different. However, this problem is much easier to formulate if we just choose to add a latent variable Z_i for trial i to indicate which generators was used. We will come back to this example after we review the basics of EM algorithm.

Intuitively, what EM does is iteratively “completes” the data by “guessing” the values of hidden variables then re-estimates the parameters by using the guessed values as true values. More specifically, EM algorithm contains two main steps: (i) an expectation step (E-step) that computes the expectation of the log-likelihood function using the current estimates for the parameters; (ii) a maximization step (M-step) that computes the estimate of the parameters to maximize the expected log-likelihood function in E-step. As we discussed in the previous section, finding the solution to a MLE problem generally requires taking derivatives of the likelihood function with respect to unknown variables (including both the estimation parameters and latent variables) and solving the resulting equations. However, in statistical models with latent variables, such approach is often not possible: the result is typically a set of inter-locking equations where the solution of the parameters requires the values of the latent variables and vice-versa, but substituting one set of equations into another produces unsolvable equations. Based on the aforementioned observation, the EM algorithm provides a numerical way to solve the two sets of inter-locking equations. It starts by picking arbitrary values of one of two sets of unknowns, use them to estimate the second set, then use the new values of the second set to better estimate the first set, and then keep iterating between the two until estimation converges.

The following is a more formal description of EM algorithm. Given a statistical model consisting a set of observed data X, a set of unobserved or missing data Z, and a vector of unknown estimation parameters θ to be estimated. The likelihood function L(θ;x) is given by:

$\begin{array}{l}\hfill L(\theta ;x)=p(x|\theta )=\sum _{z}p(x,z|\theta )\end{array}$

As we discussed earlier, the log-likelihood function is normally used to compute the MLE. Hence, we denote the log-likelihood function $l(\theta ;x)=logL(\theta ;x)$. Let us first consider the following inequality:

$\begin{array}{ll}\hfill l(\theta ;x)& =logp(x|\theta )=log\sum _{z}p(x,z|\theta )\hfill \\ \hfill & =log\sum _{z}q(z|x,\theta )\frac{p(x,z|\theta )}{q(z|x,\theta )}\hfill \\ \hfill & \ge \sum _{z}q(z|x,\theta )log\frac{p(x,z|\theta )}{q(z|x,\theta )}=F(q,\theta )\hfill \end{array}$

where q(z|x,θ) is an arbitrary density function over Z. The above inequality is called Jensen’s inequality, which basically states for a real continuous concave function: ${\sum }_{x}p(x)f(x)\le f({\sum }_{x}p(x)x)$. Instead of maximizing l(θ;x), the EM algorithm maximizes its lower bound F(q,θ) through following two steps:

$\begin{array}{l}\hfill q^{(t+1)}(z|x,{\theta }^{(t)})=\underset{q}{argmax}F(q,{\theta }^{(t)})\end{array}$

$\begin{array}{l}\hfill {\theta }^{(t+1)}=\underset{\theta }{argmax}F(q^{(t+1)}(z|x,{\theta }^{(t)}),\theta )\end{array}$

The above two steps is another interpretation of the E-step and M-step. We can start with some random initial value of parameters θ⁽⁰⁾ and iterate between the above two steps until the estimation converges. Solving Equation (3.17) while fixing θ, we can obtain q^(t+1) = p(z|x,θ^(t)). To compute Equation (3.18), we fix q and note that:

$\begin{array}{ll}\hfill F(q^{(t+1)},\theta )& =\sum _z{q}^{(t+1)}(z|x,{\theta }^{(t)})log\frac{p(x,z|\theta )}{q^{(t+1)}(z|x,{\theta }^{(t)})}\hfill \\ \hfill & =\sum _z{q}^{(t+1)}(z|x,{\theta }^{(t)})logp(x,z|{\theta }^{(t)})-\sum _z{q}^{(t+1)}(z|x,{\theta }^{(t)})log{q}^{(t+1)}(z|x,{\theta }^{(t)})\hfill \\ \hfill & =Q(\theta |{\theta }^{(t)})+H(q^{(t+1)})\hfill \end{array}$

As we mentioned earlier, maximizing l(θ;z) is equivalent to maximizing its lower bound F(q,θ). Maximizing F(q,θ) with respect to θ is equivalent to maximizing Q(θ|θ^(t)) with respect to θ. Now, we can re-interpret Equations (3.17) and 3.18 as follows:

$\begin{array}{ll}\hfill & E-step:\text{Compute}Q(\theta |{\theta }^{(t)})=E_{p(z|x,{\theta }^{(t)})}logp(x,z|\theta )\hfill \end{array}$

$\begin{array}{ll}\hfill & M-step:{\theta }^{(t+1)}=\underset{\theta }{argmax}Q(\theta |{\theta }^{(t)})\hfill \end{array}$

Equations (3.20) and 3.21 are the E-step and M-step of the EM algorithm. In E-step, we compute the expectation of the log-likelihood function with the distribution of the latent variables that depends on the observed data and θ^(t). In M-step, we compute the estimation of the θ in next round as the ones that maximize the expectation function in E-step. The algorithm iterates between the above two steps until convergence. Note that, in order to show that the EM converges to a local maximal of the likelihood surface, one need to show that log(p(x|θ^(t+1))) ≥ log(p(x|θ^(t))), which is an easy proof [94].

After introducing the EM algorithm, let us come back to the Binomial Mixture Model example we mentioned at the start of this section and apply the EM to solve it. Let us specify the definition of the latent variable: Z_i = 1 if the first binary number generator was used in the ith trial and 0 otherwise. We start by writing down the expected log-likelihood function of our problem.

$\begin{array}{ll}\hfill Q(\theta |{\theta }^{(t)})& =E\left[log\prod _{i=1}^n{[q\times p_1^{x_i}\times {(1-p_1)}^{(1-x_i)}]}^{z_i}\times {[(1-q)\times p_2^{x_i}\times {(1-p_2)}^{(1-x_i)}]}^{1-z_i}\right]\hfill \\ \hfill & =\sum _{i=1}^{n}E[z_i|x_i,{\theta }^{(t)}][logq+x_{i}log{p}_1+(1-x_i)log(1-p_1)]\hfill \\ \hfill & +(1-E[z_i|x_i,{\theta }^{(t)}])[log(1-q)+x_{i}log{p}_2+(1-x_i)log(1-p_2)]\hfill \end{array}$

Then we can compute E[z_i|x_i,θ^(t)] for E-step as:

$\begin{array}{ll}\hfill Z(i,t)& =E[z_i|x_i,{\theta }^{(t)}]=p(z_i=1|x_i,{\theta }^{(t)})\hfill \\ \hfill & =\frac{p(x_i|z_i,{\theta }^{(t)})p(z_i=1|{\theta }^{(t)})}{p(x_i|{\theta }^{(t)})}\hfill \\ \hfill & =\frac{q^{(t)}\times {[p_1^{(t)}]}^{x_i}\times {[(1-p_1^{(t)})]}^{(1-x_i)}}{q^{(t)}\times {[p_1^{(t)}]}^{x_i}\times {[(1-p_1^{(t)})]}^{(1-x_i)}+(1-q^{(t)})\times {[p_2^{(t)}]}^{x_i}\times {[(1-p_2^{(t)})]}^{(1-x_i)}}\hfill \end{array}$

Following M-step, we maximize Q(θ|θ^(t)) with respect to θ, we obtain:

$\begin{array}{ll}\hfill \frac{\partial Q(\theta |{\theta }^{(t)})}{\partial p_1}& =0:p_1^{(t+1)}=\frac{\sum _{i}Z(i,t)x_i}{\sum _{i}Z(i,t)}\hfill \\ \hfill \frac{\partial Q(\theta |{\theta }^{(t)})}{\partial p_2}& =0:p_2^{(t+1)}=\frac{\sum _i(1-Z(i,t))x_i}{\sum _i(1-Z(i,t))}\hfill \\ \hfill \frac{\partial Q(\theta |{\theta }^{(t)})}{\partial q}& =0:q^{(t+1)}=\frac{\sum _{i}Z(i,t)}{n}\hfill \end{array}$

3.6 Basics of Confidence Intervals

In statistics, a confidence interval provides an estimated range of values which is likely to include an unknown estimation parameter [95]. The confidence interval is calculated from a given set of sample data and used to indicate the reliability of the estimate. Confidence limits are the lower and upper bounds of a confidence interval, which define the range of the interval. Confidence level is the probability that the confidence interval contains the true value of the estimation parameter given a distribution of samples. For example, when we say, “we are 95% confident that the true value of the estimation parameter is in our confidence interval,” what we really mean is 95% of the observed confidence intervals will capture the true value of the parameter. However, once a sample is taken, the true value of the population parameter is either in or outside the confidence interval, it is not a matter of chance. If a corresponding hypothesis test is performed, the confidence level is the complement of the significance level (i.e., 95% confidence interval reflects a significance level of 0.05).

Now let us go through a simple example of norm distribution to better illustrate the above concepts. Suppose that a simple random sample of size n is drawn from a norm population with unknown mean μ and known standard deviation σ. Then the sample distribution is $N(\mu ,\sigma /\sqrt{n})$. Then we can use the standard norm distribution N(0,1) to compute the confidence interval for the confidence level p = 95% as shown in Figure 3.1. Here we need to introduce one more concept: standard score (also called z score). It represents the number of standard deviations that an observation is away from the mean. For example, the z score for the 95% confidence level of a standard norm distribution is 1.96. For this problem, we use the sample mean $\stackrel{-}{x}$ as an estimate for μ, then the 95% confidence interval is:

$\begin{array}{l}\hfill \left(\stackrel{-}{x}-z^{*}\frac{\sigma }{\sqrt{n}},\stackrel{-}{x}+z^{*}\frac{\sigma }{\sqrt{n}}\right)\end{array}$

In estimation theory and statistics, the CRLB is defined as the inverse of Fisher information and describes a lower bound on the estimation variance of any unbiased estimator [96]. An unbiased estimator that achieves CRLB actually achieves the lowest possible mean squared error among all unbiased estimators and is said to be efficient. To give an intuitive explanation, we provide an inform proof as follows. Let us start with the definition of an unbiased estimator $\widehat{\theta }(X)$:

$\begin{array}{l}\hfill E[\widehat{\theta }(X)-\theta |\theta ]=\int [\widehat{\theta }(x)-\theta ]\times L(x;\theta )\text{d}x=0\end{array}$

where L(x;θ) = p(x|θ) is the likelihood function we discussed in the previous section. Intuitively, if the likelihood is strongly dependent on θ (e.g., sharply peaked w.r.t. to changes in θ), it is easy to estimate the correct value of θ, and hence the data contains a lot of information about parameters. On the contrary, if the likelihood is weakly dependent on θ (e.g., flat and spread-out w.r.t. to changes in θ), then it would take many samples of data to estimate the correct value of θ. Hence the data contain much less information about the estimation parameter.

We take the derivative of Equation (3.26) with respect to θ, we get:

$\begin{array}{l}\hfill \frac{\partial }{\partial \theta }\int [\widehat{\theta }(x)-\theta ]\times L(x;\theta )\text{d}x=\int [\widehat{\theta }(x)-\theta ]\times \frac{\partial L(x;\theta )}{\partial \theta }\text{d}x-\int L(x;\theta )\text{d}x=0\end{array}$

Given the fact that L(x;θ) is a probability, we know that $\int L(x;\theta )\text{d}x=1$. From calculus, we know that $\frac{\partial L}{\partial \theta }=L\frac{\partial logL}{\partial \theta }$. We can rewrite Equation (3.27) as:

$\begin{array}{ll}\hfill & \int [\widehat{\theta }(x)-\theta ]\times L(x;\theta )\times \frac{\partial logL(x;\theta )}{\partial \theta }\text{d}x=1\hfill \\ \hfill & \int [\widehat{\theta }(x)-\theta ]\times \sqrt{L(x;\theta )}\times \sqrt{L(x;\theta )}\times \frac{\partial logL(x;\theta )}{\partial \theta }\text{d}x=1\hfill \end{array}$

If we square the above equation and use Cauchy-Schwarz inequality, we can obtain:

$\begin{array}{l}\hfill \left[\int {[\widehat{\theta }(x)-\theta ]}^2\times L(x;\theta )\text{d}x\right]\times \left[\int {\left[\frac{\partial logL(x;\theta )}{\partial \theta }\right]}^2\times L(x;\theta )\text{d}x\right]\ge 1\end{array}$

The right most factor is the Fisher information as we mentioned in Section 3.4: $I(\theta )=\int {\left[\frac{\partial logL(x;\theta )}{\partial \theta }\right]}^2\times L(x;\theta )\text{d}x$. The left most factor is the expected mean squared error (i.e., variance) of our estimation $\widehat{\theta }$:

$\begin{array}{l}\hfill Var(\widehat{\theta })=E[{(\widehat{\theta }(x)-\theta )}^2|\theta ]=\int {[\widehat{\theta }(x)-\theta ]}^2\times L(x;\theta )\text{d}x\end{array}$

Finally, we can show from the above derivation:

$\begin{array}{l}\hfill Var(\widehat{\theta })\ge \frac{1}{I(\theta )}=CRLB(\theta )\end{array}$

This equation re-states the definition of CRLB we introduced earlier, which provides an fundamental bound to quantify the estimation accuracy on the parameter θ of an unbiased estimator like MLE.

Now let us revisit the binomial example we discussed in Section 3.4 to give a concrete example of computing CRLB. The experiments in this example include n independent Bernoulli trials, with x trials succeed. The probability of each trial to succeed is p, which is the estimation parameter of our problem. We already showed the MLE $\widehat{p}=\frac{x}{n}$. In the following we compute the Fisher information to obtain the CRLB for our estimate. We denote the likelihood function as $L(x;p)=\left(\genfrac{}{}{0.0pt}{}{n}{x}\right)p^x{(1-p)}^{(n-x)}$

$\begin{array}{ll}\hfill I(p)& =-E\left[\frac{{\partial }^2}{\partial p^2}log(L(x;p))|p\right]\hfill \\ \hfill & =-E\left[\frac{{\partial }^2}{\partial p^2}log\left.\left(p^x{(1-p)}^{(n-x)}\frac{n!}{x!(n-x)!}\right)\right|p\right]\hfill \\ \hfill & =-E\left[\frac{{\partial }^2}{\partial p^2}(xlogp+(n-x)log(1-p))|p\right]\hfill \\ \hfill & =-E\left[\frac{\partial }{\partial p}\left.\left(\frac{x}{p}-\frac{n-x}{1-p}\right)\right|p\right]\hfill \\ \hfill & =E\left[\left.\left(\frac{x}{p^2}+\frac{n-x}{{(1-p)}^2}\right)\right|p\right]\hfill \\ \hfill & =\frac{np}{p^2}+\frac{n(1-p)}{{(1-p)}^2}\hfill \\ \hfill & =\frac{n}{p(1-p)}\hfill \end{array}$

Hence, the CRLB is the inverse of Fisher information, which is $\frac{p(1-p)}{n}$ in this case.

3.7 Putting It All Together

After we reviewed several concepts and methods from statistics and estimation theory in previous sections, we will discuss, in this section, a generic network model for social sensing where we can put everything together under the same framework.

As we discussed earlier, in social sensing, a group of participants (sources) with unknown reliability collectively report observations about the physical world. Since we usually are not certain about the correctness of the observations, we call the collected data claims. This basic data collection paradigm can be represented by a graph model as shown in Figure 3.2. In this model, nodes on the left represent participants (sources) and nodes on the right represent claims. The links connecting two types of nodes in the graph describe “who said what.” For simplicity, in the basic model, claims are assumed to be binary (either true or false). This network abstraction belongs to heterogeneous networks that are discussed in Section 3.2 since there are two types of nodes in the network. What we are interested in social sensing context is the attributes of the nodes in the network. For example, what is the reliability of sources (i.e., the likelihood of a particular source to generate true claims)? What is the correctness of claims (i.e., the probability of a particular claim to be true)? This problem is trivial if we either know the source reliability or the claim correctness in advance. However, one key challenge in social sensing is that we are aware of neither the source reliability nor the claim correctness a priori.

This book reviews a series of recent work that address the data reliability challenge under the same analytic framework. In particular, Chapter 4 reviews the sate-of-the-art fact-finders as well as a Bayesian interpretation of the basic fact-finding scheme used in generic network analysis. To overcome some fundamental limitations of the basic fact-finding scheme, Chapter 5 reviews a MLE framework by leveraging the MLE principle discussed in Section 3.4. This MLE framework allows applications to jointly estimate both the reliability of sources and the correctness of claims to obtain the optimal solutions that are most consistent with the data observed. In order to quantify the accuracy of the MLE, Chapter 6 reviews a quantification scheme based on CRLB discussed in Section 3.6. After that, we will review the work that study different extensions and generalizations of the basic MLE model. Chapter 7 reviews the extension of the basic model where observations can be conflicting and claims can be non-binary. Chapter 8 reviews the generalization of the model where dependencies between sources (e.g., links in social networks) are explicitly considered. Chapter 9 reviews the further generalization of the model where the dependencies between claims (e.g., correlations between variables in physical network) are considered. Chapter 10 reviews a recursive version of the model that is tailored to better handle streaming data. In the remaining of this book, we will review these exciting progress and discoveries in social sensing.