If we are using the perfect VaR model, then given all the information available to us at the time the VaR forecast is made, we should not be able to predict whether the VaRwill be violated. Our forecast of the probability of a VaR violation should be simply p every day. If we could predict the VaR violations, then that information could be used to construct a better risk model. In other words, the hit sequence of violations should be completely unpredictable and therefore distributed independently over time as a Bernoulli variable that takes the value 1 with probability p and the value 0 with probability (1 − p). We write

If p is 1/2, then the i.i.d. Bernoulli distribution describes the distribution of getting a “head” when tossing a fair coin. The Bernoulli distribution function is written

When backtesting risk models, p will not be 1/2 but instead on the order of 0.01 or 0.05 depending on the coverage rate of the VaR. The hit sequence from a correctly specified risk model should thus look like a sequence of random tosses of a coin, which comes up heads 1% or 5% of the time depending on the VaR coverage rate.

We first want to test if the fraction of violations obtained for a particular risk model, call it π, is significantly different from the promised fraction, p. We call this the unconditional coverage hypothesis. To test it, we write the likelihood of an i.i.d. Bernoulli(π) hit sequence

where T₀ and T₁ are the number of 0s and 1s in the sample. We can easily estimate π from ; that is, the observed fraction of violations in the sequence. Plugging the maximum likelihood (ML) estimates back into the likelihood function gives the optimized likelihood as

Under the unconditional coverage null hypothesis that π = p, where p is the known VaR coverage rate, we have the likelihood

We can check the unconditional coverage hypothesis using a likelihood ratio test

Asymptotically, that is, as the number of observations, T goes to infinity, the test will be distributed as a with one degree of freedom. Substituting in the likelihood functions, we write

The larger the value is the more unlikely the null hypothesis is to be true. Choosing a significance level of say 10% for the test, we will have a critical value of 2.7055 from the distribution. If the test value is larger than 2.7055, then we reject the VaR model at the 10% level. Alternatively, we can calculate the P-value associated with our test statistic. The P-value is defined as the probability of getting a sample that conforms even less to the null hypothesis than the sample we actually got given that the null hypothesis is true. In this case, the P-value is calculated as

where denotes the cumulative density function of a variable with one degree of freedom. If the P-value is below the desired significance level, then we reject the null hypothesis. If we, for example, obtain a test value of 3.5, then the associated P-value is

If we have a significance level of 10%, then we would reject the null hypothesis, but if our significance level is only 5%, then we would not reject the null that the risk model is correct on average.

The choice of significance level comes down to an assessment of the costs of making two types of mistakes: We could reject a correct model (Type I error) or we could fail to reject (that is, accept) an incorrect model (Type II error). Increasing the significance level implies larger Type I errors but smaller Type II errors and vice versa. In academic work, a significance level of 1%, 5%, or 10% is typically used. In risk management, the Type II errors may be very costly so that a significance level of 10% may be appropriate.

Often, we do not have a large number of observations available for backtesting, and we certainly will typically not have a large number of violations, T₁, which are the informative observations. It is therefore often better to rely on Monte Carlo simulated P-values rather than those from the distribution. The simulated P-values for a particular test value can be calculated by first generating 999 samples of random i.i.d. Bernoulli(p) variables, where the sample size equals the actual sample at hand. Given these artificial samples we can calculate 999 simulated test statistics, call them The simulated P-value is then calculated as the share of simulated values that are larger than the actually obtained 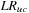test value. We can write

where takes on the value of one if the argument is true and zero otherwise.

To calculate the tests in the first place, we need samples where VaR violations actually occurred; that is, we need some ones in the hit sequence. If we, for example, discard simulated samples with zero or one violations before proceeding with the test calculation, then we are in effect conditioning the test on having observed at least two violations.

Imagine all the VaR violations or “hits” in a sample happening around the same time, which was the case in Figure 13.1. Would you then be happy with a VaR with correct average (or unconditional) coverage? The answer is clearly no. For example, if the 5% VaR gave exactly 5% violations but all of these violations came during a three-week period, then the risk of bankruptcy would be much higher than if the violations came scattered randomly through time. We therefore would very much like to reject VaR models that imply violations that are clustered in time. Such clustering can easily happen in a VaR constructed from the Historical Simulation method in Chapter 2, if the underlying portfolio return has a clustered variance, which is common in asset returns and which we studied in Chapter 4.

If the VaR violations are clustered, then the risk manager can essentially predict that if today is a violation, then tomorrow is more than likely to be a violation as well. This is clearly not satisfactory. In such a situation, the risk manager should increase the VaR in order to lower the conditional probability of a violation to the promised p.

Our task is to establish a test that will be able to reject a VaR with clustered violations. To this end, assume the hit sequence is dependent over time and that it can be described as a so-called first-order Markov sequence with transition probability matrix

These transition probabilities simply mean that conditional on today being a nonviolation (that is, I_t = 0), then the probability of tomorrow being a violation (that is, ) is π₀₁. The probability of tomorrow being a violation given today is also a violation is defined by

Similarly, the probability of tomorrow being a violation given today is not a violation is defined by

The first-order Markov property refers to the assumption that only today's outcome matters for tomorrow's outcome—that the exact sequence of past hits does not matter, only the value of I_t matters. As only two outcomes are possible (zero and one), the two probabilities π₀₁ and π₁₁ describe the entire process. The probability of a nonviolation following a nonviolation is and the probability of a nonviolation following a violation is

If we observe a sample of T observations, then we can write the likelihood function of the first-order Markov process as

where T_ij, i, j = 0, 1 is the number of observations with a j following an i. Taking first derivatives with respect to π₀₁ and π₁₁ and setting these derivatives to zero, we can solve for the maximum likelihood estimates

Using then the fact that the probabilities have to sum to one, we have

which gives the matrix of estimated transition probabilities

Allowing for dependence in the hit sequence corresponds to allowing π₀₁ to be different from π₁₁. We are typically worried about positive dependence, which amounts to the probability of a violation following a violation (π₁₁) being larger than the probability of a violation following a nonviolation (π₀₁). If, on the other hand, the hits are independent over time, then the probability of a violation tomorrow does not depend on today being a violation or not, and we write Under independence, the transition matrix is thus

We can test the independence hypothesis that using a likelihood ratio test

where is the likelihood under the alternative hypothesis from the test.

In large samples, the distribution of the test statistic is also with one degree of freedom. But we can calculate the P-value using simulation as we did before. We again generate 999 artificial samples of i.i.d. Bernoulli variables, calculate 999 artificial test statistics, and find the share of simulated test values that are larger than the actual test value.

As a practical matter, when implementing the 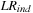tests we may incur samples where In this case, we simply calculate the likelihood function as

Ultimately, we care about simultaneously testing if the VaR violations are independent and the average number of violations is correct. We can test jointly for independence and correct coverage using the conditional coverage test

which corresponds to testing that

Notice that the test takes the likelihood from the null hypothesis in the test and combines it with the likelihood from the alternative hypothesis in the test. Therefore,

so that the joint test of conditional coverage can be calculated by simply summing the two individual tests for unconditional coverage and independence. As before, the P-value can be calculated from simulation.

In Chapter 1 we used the autocorrelation function (ACF) to assess the dependence over time in returns and squared returns. We can of course use the ACF to assess dependence in the VaR hit sequence as well. Plotting the hit-sequence autocorrelations against their lag order will show if the risk model gives rise to autocorrelated hits, which it should not.

As in Chapter 3, the statistical significance of a set of autocorrelations can be formally tested using the Ljung-Box statistic. It tests the null hypothesis that the autocorrelation for lags 1 through m are all jointly zero via

where is the autocorrelation of the VaR hit sequence for lag order τ. The chi-squared distribution with m degrees of freedom is denoted by . We reject the null hypothesis that the hit autocorrelations for lags 1 through m are jointly zero when the test value is larger than the critical value in the chi-squared distribution with m degrees of freedom.

Consider regressing the hit sequence on the vector of known variables, X_t. In a simple linear regression, we would have

where the error term is assumed to be independent of the regressor, X_t.

The hypothesis that is then equivalent to

As X_t is known, taking expectations yields

which can only be true if b₀ = p and b₁ is a vector of zeros. In this linear regression framework, the null hypothesis of a correct risk model would therefore correspond to the hypothesis

which can be tested using a standard F-test (see the econometrics textbooks referenced at the end of Chapter 3). The P-value from the test can be calculated using simulated samples as described earlier.

There is, of course, no particular reason why the explanatory variables should enter the conditional expectation in a linear fashion. But nonlinear functional forms could be tested as well.

In risk management, we often only really care about forecasting the left tail of the distribution correctly. Testing the entire distribution as we did earlier may lead us to reject risk models that capture the left tail of the distribution well, but not the rest of the distribution. Instead, we should construct a test that directly focuses on assessing the risk model's ability to capture the left tail of the distribution, which contains the largest losses.

Consider restricting attention to the tail of the distribution to the left of the 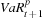—that is, to the largest losses.

If we want to test that the observations from, for example, the 10% largest losses are themselves uniform, then we can construct a rescaled variable as

Then we can write the null hypothesis that the risk model provides the correct tail distribution as

or equivalently

Figure 13.3 shows the histogram of corresponding to the 10% smallest returns. The data again follow a Student's t(d) distribution with d = 6 but the density forecast model assumes the normal distribution. We have simply zoomed in on the leftmost 10% of the histogram from Figure 13.2. The systematic deviation from a flat histogram is again obvious.

To do formal statistical testing, we can again construct an alternative hypothesis as in

for t + 1 such that We can then calculate a likelihood ratio test

where nb again is the number of elements in the parameter vector b₁.

Standard implementation of stress testing amounts to defining a set of scenarios, running them through the risk model using the current portfolio weights, and if a scenario results in an extreme loss, then the portfolio manager may decide to rebalance the portfolio. Notice how this is very different from deciding to rebalance the portfolio based on an undesirably high VaR or Expected Shortfall (ES). VaR and ES are proper probabilistic statements: What is the loss such that I will lose more only 1% of the time (VaR)? Or what is the expected loss when I exceed my VaR(ES)? Standard stress testing does not tell the portfolio manager anything about the probability of the scenario happening, and it is therefore not at all clear what the portfolio rebalancing decision should be. The portfolio manager may end up overreacting to an extreme scenario that occurs with very low probability, and underreact to a less extreme scenario that occurs much more frequently. Unless a probability of occurring is assigned to each scenario, then the portfolio manager really has no idea how to react.

On the other hand, once scenario probabilities are assigned, then stress testing can be very useful. To be explicit, consider a simple example of one stress scenario, which we define as a probability distribution of the vector of factor returns. We simulate a vector of risk factor returns from the risk model, calling it and we also simulate from the scenario distribution, . If we assign a probability α of a draw from the scenario distribution occurring, then we can combine the two distributions as in

Data from the combined distribution is generated by drawing a random variable U_i from a Uniform(0,1) distribution. If U_i is smaller than α, then we draw a return from ; otherwise we draw it from The combined distribution can easily be generalized to multiple scenarios, each of which has its own preassigned probability of occurring.

Notice that by simulating from the combined distribution, we are effectively creating a new data set that reflects our available historical data as well our view of the deficiencies of it. The deficiencies are rectified by including data from the stress scenarios in the new combined data set.

Once we have simulated data from the combined data set, we can calculate the VaR or ES risk measure on the combined data using the previous risk model. If the risk measure is viewed to be inappropriately high then the portfolio can be rebalanced. Notice that now the rebalancing is done taking into account both the magnitude of the stress scenarios and their probability of occurring.

Assigning the probability, α, also allows the risk manager to backtest the VaR system using the combined probability distribution . Any of these tests can be used to test the risk model using the data drawn from If the risk model, for example, has too many VaR violations on the combined data, or if the VaR violations come in clusters, then the risk manager should consider respecifying the risk model. Ultimately, the risk manager can use the combined data set to specify and estimate the risk model.

Having decided to do stress testing, a key challenge to the risk manager is to create relevant scenarios. The scenarios of interest will typically vary with the type of portfolio under management and with the factor returns applied. The exact choice of scenarios will therefore be situation specific, but in general, certain types of scenarios should be considered. The risk manager ought to do the following:

Even if we have identified a set of scenario types, pinpointing the specific scenarios is still difficult. But the long and colorful history of financial crises may serve as a source of inspiration. Examples could include crises set off by political events or natural disasters. For example, the 1995 Nikkei crisis was set off by the Kobe earthquake, and the 1979 oil crisis was rooted in political upheaval. Other crises such as the 1997 Thai baht float and subsequent depreciation mentioned earlier could be the culmination of pressures such as a continuing real appreciation building over time resulting in a loss of international competitiveness.

The effects of market crises can also be very different. They can result in relatively brief market corrections, as was the case after the October 1987 stock market crash, or they can have longer lasting effects, such as the Great Depression in the 1930s. Figure 13.4 depicts the 15 largest daily declines in the Dow Jones Industrial Average during the past 100 years.

Figure 13.4 clearly shows that the October 19, 1987, decline was very large even on a historical scale. We see that the second dip arriving a week later on October 26, 1987 was large by historical standards as well: It was the tenth-largest daily drop. The 2008–2009 financial crisis shows up in Figure 13.4 with three daily drops in the top 15. None of them are in the top 10 however. October–November 1929, which triggered the Great Depression, has four daily drops in the top 10—three of them in the top 5. This bunching in time of historically large daily market drops is quite striking. It strongly suggests that extremely large market drops do not occur randomly but are instead driven by market volatility being extraordinarily high. Carefully modeling volatility dynamics as we did in Chapter 4 and Chapter 5 is therefore crucial.

Figure 13.5 shows nine episodes of prolonged market downturn—or bear markets—which we define as at least a 30% decline lasting for at least 50 days. Figure 13.5 shows that the bear market following the 1987 market crash was relatively modest compared to previous episodes. The 2008–2009 bear market during the recent financial crises was relatively large at 50%.

Figure 13.5 suggests that stress testing scenarios should include both rapid corrections, such as the 1987 episode, as well as prolonged downturns that prevailed in 2008–2009.

The Filtered Historical Simulation (or bootstrapping) method developed in Chapter 8 to construct the term structure of risk can be used to stress test the term structure of risk as well. Rather than feeding randomly drawn shocks through the model over time we can feed a path of historical shocks from a stress scenario through the model. The stress scenario can for example be the string of daily shocks observed from September 2008 through March 2009. The outcome of this simulation will show how a stressed market scenario will affect the portfolio under consideration.