8. Simulating the Term Structure of Risk
This chapter introduces simulation methods for computing VaR and ES when the horizon of interest is longer than one day. The simulation based methods introduced here allow the risk manager to use dynamic risk models to compute VaR and ES at any horizon of interest and therefore to compute the entire term structure of risk. We will introduce two techniques: Monte Carlo simulation, which relies on artificial random numbers, and Filtered Historical Simulation, which uses historical random shocks. First, we will consider simulating forward univariate risk models. Second, we simulate forward in time multivariate risk models with constant correlations across assets. Third, we simulate multivariate risk models with dynamic correlations.
Keywords: Monte Carlo simulation, Filtered Historical Simulation, bootstrapping, random number generation
1. Chapter Overview
So far we have focused on the task of computing VaR and ES for the one-day-ahead horizon only. The dynamic risk models we have introduced have closed-form solutions for one-day-ahead VaR and ES but not when the horizon of interest is longer than one day. In this case we need to rely on simulation methods for computing VaR and ES. This chapter introduces two methods for doing so. The simulation-based methods introduced here allow the risk manager to use the dynamic risk model to compute VaR and ES at any horizon of interest and therefore to compute the entire term structure of risk. By analogy with the term structure of variance plots in Chapter 4 we refer to the term structure of risk as the VaR(or ES) plotted against the horizon of interest.
The chapter proceeds as follows:
• First, we will consider simulating forward the univariate risk models from Part II of the book. We will introduce two techniques: Monte Carlo simulation, which relies on artificial random numbers, and Filtered Historical Simulation (FHS), which uses historical random shocks.
• Second, we simulate forward in time multivariate risk models with constant correlations across assets. Again we will consider Monte Carlo as well as FHS.
• Third, we simulate multivariate risk models with dynamic correlations using the DCC model from Chapter 7.
We are assuming that the portfolio variance (in the case of univariate risk models) and individual asset variances (in the case of multivariate risk models) have already been modeled and estimated on historical returns using the techniques in Chapter 4 and Chapter 5. We are also assuming that the correlation dynamics have been modeled and estimated using the DCC model in Chapter 7.
For convenience we are assuming normally distributed variables when doing Monte Carlo simulation in this chapter. Chapter 9 will provide the details on simulating random variables from the t distribution.
2. The Risk Term Structure in Univariate Models
In the simplistic case, where portfolio returns are normally distributed with a constant variance,  , the returns over the next K days are also normally distributed, but with variance
, the returns over the next K days are also normally distributed, but with variance  . In that case, we can easily calculate the VaR for returns over the next K days calculated on day t, as
. In that case, we can easily calculate the VaR for returns over the next K days calculated on day t, as
In the much more realistic case where the portfolio variance is time varying, going from 1-day-ahead to K-days-ahead VaR is not so simple. As we saw in Chapter 4, the variance of the K-day return is in general
In the simple RiskMetrics variance model, where  we get
we get
In the symmetric GARCH(1,1) model, where  , we instead get
, we instead get
In the GARCH case, the variance does mean revert and it therefore does not scale by the horizon K, and again the returns over the next K days are not normally distributed, even if the 1-day returns are assumed to be. However, a nice feature of mean-reverting GARCH models is that as K gets large, the return distribution does approach the normal. This appears to be a common feature of real-life return data as we argued in Chapter 1.
The upshot is that we are faced with the challenge of computing risk measures such as VaR at multiday horizons, without knowing the analytical form for the distribution of returns at those horizons. Fortunately, this challenge can be met through the use of Monte Carlo simulation techniques.
In Chapter 1 we discussed two stylized facts regarding the mean or average daily return—first, that it is very difficult to forecast, and, second that it is very small relative to the daily standard deviation. At a longer horizon, it is still fairly difficult to forecast the mean but its relative importance increases with horizon. Consider a simple example where daily returns are normally distributed with a constant mean and variance as in
The K-day return in this case is distributed as
Although the mean return is potentially important at longer horizons, in order to save on notation, we will still assume that the mean is zero in the sections that follow. However, it is easy to generalize the analysis to include a nonzero mean.
2.1. Monte Carlo Simulation
We illustrate the power of Monte Carlo simulation (MCS) through a simple example. Consider our GARCH(1,1)-normal model of returns, where
As mentioned earlier, at the end of day t we obtain Rt and we can calculate  , which is tomorrow's variance in the GARCH model.
, which is tomorrow's variance in the GARCH model.
Using random number generators, which are standard in most quantitative software packages, we can generate a set of artificial (or pseudo) random numbers
From these random numbers we can calculate a set of hypothetical returns for tomorrow as
Graphically, we can illustrate the simulation of hypothetical daily returns from day t + 1 to day t + K as

Each row corresponds to a so-called Monte Carlo simulation path, which branches out from 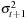 on the first day, but which does not branch out after that. On each day a given branch gets updated with a new random number, which is different from the one used any of the days before. We end up with MC sequences of hypothetical daily returns for day t + 1 through day t + K. From these hypothetical future daily returns, we can easily calculate the hypothetical K-day return from each Monte Carlo path as
on the first day, but which does not branch out after that. On each day a given branch gets updated with a new random number, which is different from the one used any of the days before. We end up with MC sequences of hypothetical daily returns for day t + 1 through day t + K. From these hypothetical future daily returns, we can easily calculate the hypothetical K-day return from each Monte Carlo path as
If we collect these MC hypothetical K-day returns in a set  then we can calculate the K-day value at risk simply by calculating the 100pth percentile as in
then we can calculate the K-day value at risk simply by calculating the 100pth percentile as in
Notice that in contrast to the HS and WHS techniques introduced in Chapter 2, the GARCH-MCS method outlined here is truly conditional in nature as it builds on today's estimate of tomorrow's variance, 
A key advantage of the MCS technique is its flexibility. We can use MCS for any assumed distribution of standardized returns—normality is not required. If we think the standardized t(d) distribution with d = 12 for example describes the data better, then we simply draw from this distribution. Commercial software packages typically contain the regular t(d) distribution, but we can standardize these draws by multiplying by  as we saw in Chapter 6. Furthermore, the MCS technique can be used for any fully specified dynamic variance model.
as we saw in Chapter 6. Furthermore, the MCS technique can be used for any fully specified dynamic variance model.
In Figure 8.1 we apply the NGARCH model for the S&P 500 from Chapter 4 along with a normal distribution assumption. We use Monte Carlo simulation to construct and plot VaR per day,  as a function of horizon K for two different values of
as a function of horizon K for two different values of  . In the top panel the initial volatility is one-half the unconditional level and in the bottom panel
. In the top panel the initial volatility is one-half the unconditional level and in the bottom panel  is three times the unconditional level. The horizon goes from 1 to 500 trading days, corresponding roughly to two calendar years.
is three times the unconditional level. The horizon goes from 1 to 500 trading days, corresponding roughly to two calendar years.
The VaR coverage level p is set to 1%. Figure 8.1 gives a VaR-based picture of the term structure of risk. Perhaps surprisingly the term structure of VaR is initially upward sloping both when volatility is low and when it is high. The VaR term structure is driven partly by the variance term structure, which is upward sloping when current volatility is low and downward sloping when current volatility is high as we saw in Chapter 4. But the VaR term structure is also driven by the term structure of skewness and kurtosis and other moments. Kurtosis is strongly increasing at short horizons and then decreasing for longer horizons. This hump-shape in the term structure of kurtosis creates the hump in the VaR that we see in the bottom panel of Figure 8.1 when the initial volatility is high.
The coverage level p is again set to 1% and the horizon goes from 1 to 500 trading days. Figure 8.2 gives an ES-based picture of the term structure of risk, which is clearly qualitatively similar to the term structure of VaR in Figure 8.1. Note however, that the slope of the ES term structure in the upper panel of Figure 8.2 is steeper than the corresponding VaR term structure in the upper panel of Figure 8.2. Note also that the hump in the ES term structure in the bottom panel of Figure 8.2 is more pronounced than the hump in the VaR term structure in the upper panel of Figure 8.1.
2.2. Filtered Historical Simulation (FHS)
In the book so far, we have discussed methods that take very different approaches: Historical Simulation (HS) in Chapter 2 is a completely model-free approach, which imposes virtually no structure on the distribution of returns: the historical returns calculated with today's weights are used directly to calculate a percentile. The GARCH Monte Carlo simulation (MCS) approach in this chapter takes the opposite view and assumes parametric models for variance, correlation (if a disaggregate model is estimated), and the distribution of standardized returns. Random numbers are then drawn from this distribution to calculate the desired risk measure.
Both of these extremes in the model-free/model-based spectrum have pros and cons. Taking a model-based approach (MCS, for example) is good if the model is a fairly accurate description of reality. Taking a model-free approach (HS, for example) is sensible in that the observed data may capture features of the returns distribution that are not captured by any standard parametric model.
The Filtered Historical Simulation (FHS) approach, which we introduced in Chapter 6, attempts to combine the best of the model-based with the best of the model-free approaches in a very intuitive fashion. FHS combines model-based methods of variance with model-free methods of the distribution of shocks.
Assume we have estimated a GARCH-type model of our portfolio variance. Although we are comfortable with our variance model, we are not comfortable making a specific distributional assumption about the standardized returns, such as a normal or a  distribution. Instead, we would like the past returns data to tell us about the distribution directly without making further assumptions.
distribution. Instead, we would like the past returns data to tell us about the distribution directly without making further assumptions.
To fix ideas, consider again the simple example of a GARCH(1,1) model:
Given a sequence of past returns,  , we can estimate the GARCH model and calculate past standardized returns from the observed returns and from the estimated standard deviations as
, we can estimate the GARCH model and calculate past standardized returns from the observed returns and from the estimated standard deviations as
Moving forward now, at the end of day t we obtain Rt and we can calculate  , which is day t + 1's variance in the GARCH model. Instead of drawing random
, which is day t + 1's variance in the GARCH model. Instead of drawing random  s from a random number generator, which relies on a specific distribution, we can draw with replacement from our own database of past standardized residuals,
s from a random number generator, which relies on a specific distribution, we can draw with replacement from our own database of past standardized residuals,  The random drawing can be operationalized by generating a discrete uniform random variable distributed from 1 to m. Each draw from the discrete distribution then tells us which τ and thus which
The random drawing can be operationalized by generating a discrete uniform random variable distributed from 1 to m. Each draw from the discrete distribution then tells us which τ and thus which  to pick from the set
to pick from the set  .
.
We again build up a distribution of hypothetical future returns as

We end up with FH sequences of hypothetical daily returns for day t + 1 through day t + K. From these hypothetical daily returns, we calculate the hypothetical K-day returns as
If we collect the FH hypothetical K-day returns in a set  then we can calculate the K-day Value-at-Risk simply by calculating the 100pth percentile as in
then we can calculate the K-day Value-at-Risk simply by calculating the 100pth percentile as in
The ES measure can again be calculated from the simulated returns by simply taking the average of all the  s that fall below the
s that fall below the  number; that is,
number; that is,
An interesting and useful feature of FHS as compared with simple HS is that it can generate large losses in the forecast period, even without having observed a large loss in the recorded past returns. Consider the case where we have a relatively large negative z in our database, which occurred on a relatively low variance day. If this z gets combined with a high variance day in the simulation period then the resulting hypothetical loss will be large.
In Figure 8.3 we use the FHS approach based on the NGARCH model for the S&P 500 returns. We use the NGARCH-FHS model to construct and plot the  per day as a function of horizon K for two different values of
per day as a function of horizon K for two different values of  . In the top panel the initial volatility is one-half the unconditional level and in the bottom panel
. In the top panel the initial volatility is one-half the unconditional level and in the bottom panel  is three times the unconditional level. The horizons goes from 1 to 500 trading days, corresponding roughly to two calendar years.
is three times the unconditional level. The horizons goes from 1 to 500 trading days, corresponding roughly to two calendar years.
The VaR coverage level p is set to 1% again. Comparing Figure 8.3 with Figure 8.1 we see that for this S&P 500 portfolio the Monte Carlo and FHS simulation methods give roughly equal VaR term structures when the initial volatility is the same.
In Figure 8.4 we plot the  per day against horizon K.
per day against horizon K.
The coverage level p is again set to 1% and the horizon goes from 1 to 500 trading days. The FHS-based ES term structure in Figure 8.4 closely resembles the NGARCH Monte Carlo-based ES term structure in Figure 8.2.
We close this section by reemphasizing that the FHS method suggested here combines a conditional model for variance with a Historical Simulation method for the standardized returns. FHS thus captures the current level of market volatility via  but we do not need to make assumptions about the tail distribution. The FHS method has been found to perform very well in several studies and it should be given serious consideration by any risk management team.
but we do not need to make assumptions about the tail distribution. The FHS method has been found to perform very well in several studies and it should be given serious consideration by any risk management team.
3. The Risk Term Structure with Constant Correlations
The univariate methods discussed in Section 2 are useful if the main purpose of the risk model is risk measurement. If instead the model is required for active risk management including deciding on optimal portfolio allocations, or VaR sensitivities to allocation changes, then a multivariate model is required. In this section, we use the multivariate models built in Chapter 7 to simulate VaR and ES for different maturities. The multivariate risk models allow us to compute risk measures for different hypothetical portfolio allocations without having to reestimate model parameters.
We will assume that the risk manager knows his or her set of assets of interest. This set can either contain all the assets in the portfolio or a smaller set of base assets, which are believed to be the main drivers of risk in the portfolio. Base asset choices are, of course, portfolio-specific, but typical examples include equity indices, bond indices, and exchange rates as well as more fundamental economic drivers such as oil prices and real estate prices as discussed in Chapter 7.
Once the set of assets has been determined, the next step in the multivariate model is to estimate a dynamic volatility model of the type in Chapter 4 and Chapter 5 for each of the n assets. When this is complete, we can write the n asset returns in vector form as follows:
Now, define the conditional covariance matrix of the returns as
When simulating the multivariate model forward we face a new challenge, namely, that we must ensure that the vector of shocks have the correct correlation matrix,  . Random number generators provide us with uncorrelated random standard normal variables,
. Random number generators provide us with uncorrelated random standard normal variables,  , and we must correlate them before using them to simulate returns forward.
, and we must correlate them before using them to simulate returns forward.
In the case of two uncorrelated shocks, we have
In the bivariate case we have that
We can also verify the  matrix by multiplying it by its transpose
matrix by multiplying it by its transpose
In the case of n > 2 assets we need to use a so-called Cholesky decomposition or a spectral decomposition of  to compute
to compute  . See the references for details on these methods.
. See the references for details on these methods.
3.1. Multivariate Monte Carlo Simulation
In order to simulate the model forward in time using Monte Carlo we need to assume a multivariate distribution of the vector of shocks,  . In this chapter we will rely on the multivariate standard normal distribution because it is convenient and so allows us to focus on the issues involved in simulation. In Chapter 9 we will look at more complicated multivariate t distributions.
. In this chapter we will rely on the multivariate standard normal distribution because it is convenient and so allows us to focus on the issues involved in simulation. In Chapter 9 we will look at more complicated multivariate t distributions.
The algorithm for multivariate Monte Carlo simulation is as follows:
• First, draw a vector of uncorrelated random normal variables  with a mean of zero and a variance of one.
with a mean of zero and a variance of one.
• Second, use the matrix square root  to correlate the random variables; this gives
to correlate the random variables; this gives  .
.
• Third, update the variances for each asset using the approach in Section 2.
• Fourth, compute returns for each asset using the approach in Section 2.
Loop through these four steps from day t + 1 until day t + K. Now we can compute the portfolio return using the known portfolio weights and the vector of simulated returns on each day.
Repeating these steps  times gives a Monte Carlo distribution of portfolio returns. From these MC portfolio returns we can compute VaR and ES from the simulated portfolio returns as in Section 2.
times gives a Monte Carlo distribution of portfolio returns. From these MC portfolio returns we can compute VaR and ES from the simulated portfolio returns as in Section 2.
3.2. Multivariate Filtered Historical Simulation
Multivariate Filtered Historical Simulation can be done easily when we assume constant correlations.
• First, draw a vector (across assets) of historical shocks from a particular day in the historical sample of shocks, and use that to simulate tomorrow's shock, 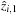 . The key insight is that when we draw the entire vector (across assets) of historical shocks from the same day, they will preserve the correlation across assets that existed historically as long as correlations are constant over time.
. The key insight is that when we draw the entire vector (across assets) of historical shocks from the same day, they will preserve the correlation across assets that existed historically as long as correlations are constant over time.
• Second, update the variances for each asset using the approach in Section 2.
• Third, compute returns for each asset using the approach in Section 2.
Loop through these steps from day t + 1 until day t + K. Now we can compute the portfolio return using the known portfolio weights and the vector of simulated returns on each day as before.
Repeating these steps  times gives a simulated distribution of portfolio returns. From these FH portfolio returns we can compute VaR and ES from the simulated portfolio returns as in Section 2.
times gives a simulated distribution of portfolio returns. From these FH portfolio returns we can compute VaR and ES from the simulated portfolio returns as in Section 2.
4. The Risk Term Structure with Dynamic Correlations
We now consider the more complicated case where the correlations are dynamic as in the DCC model in Chapter 7. We again have
Now, we have
4.1. Monte Carlo Simulation with Dynamic Correlations
As mentioned before, random number generators typically provide us with uncorrelated random standard normal variables,  , and we must correlate them before simulating returns forward.
, and we must correlate them before simulating returns forward.
At the end of day t the GARCH and DCC models provide us with  and
and  without having to do simulation. We can therefore compute a random return for day t + 1 as
without having to do simulation. We can therefore compute a random return for day t + 1 as
Using the new simulated shock vector,  , we can update the volatilities and correlations using the GARCH models and the DCC model. We thus obtain simulated
, we can update the volatilities and correlations using the GARCH models and the DCC model. We thus obtain simulated  and
and  . Drawing a new vector of uncorrelated shocks,
. Drawing a new vector of uncorrelated shocks,  , enables us to simulate the return for the second day ahead as
, enables us to simulate the return for the second day ahead as
We continue this simulation from day t + 1 through day t + K, and repeat it for  vectors of simulated shocks on each day. As before we can compute the portfolio return using the known portfolio weights and the vector of simulated returns on each day. From these MC portfolio returns we can compute VaR and ES from the simulated portfolio returns as in Section 2.
vectors of simulated shocks on each day. As before we can compute the portfolio return using the known portfolio weights and the vector of simulated returns on each day. From these MC portfolio returns we can compute VaR and ES from the simulated portfolio returns as in Section 2.
In Figure 8.5 we use the DCC model for S&P 500 returns and the 10-year treasury bond index from Chapter 7 to plot the expected future correlations. We have assumed four different values of the current correlation, ranging from −0.5 in the blue line to +0.5 in the purple line. Note that over the 60-day horizon considered, the correlations converge toward the long-run correlation value but significant differences remain even after 60 days.
 |
| Figure 8.5 |
In Chapter 4 we saw how the expected future variance can be computed analytically from current variance using the GARCH model dynamics. The key equations were repeated in Section 2. Unfortunately for dynamic correlation models, such exact analytical formulas for expected future correlation do not exist. We need to rely on the simulation methods developed here in order to construct correlation forecasts for more than one day ahead. If we for example want to construct a forecast for the correlation matrix two days ahead we can use
4.2. Filtered Historical Simulation with Dynamic Correlations
When correlations across assets are assumed to be constant then FHS is relatively easy because we can draw from historical asset shocks, using the entire vector (across assets) of historical shocks. The (constant) historical correlation will be preserved in the simulated shocks. When correlations are dynamic then we need to ensure that the correlation dynamics are simulated forward but in FHS we still want to use the historical shocks.
In this case we must first create a database of historical dynamically uncorrelated shocks from which we can resample. We create the dynamically uncorrelated historical shock as
When calculating the multiday conditional VaR and ES from the model, we again need to simulate daily returns forward from today's (day t) forecast of tomorrow's matrix of volatilities,  and correlations,
and correlations,  .
.
From the database of uncorrelated shocks  , we can draw a random vector of historical uncorrelated shocks, called
, we can draw a random vector of historical uncorrelated shocks, called  . It is important to note that in order to preserve asset-specific characteristics and potential nonlinear dependence in the shocks, we draw an entire vector representing the same day for all the assets.
. It is important to note that in order to preserve asset-specific characteristics and potential nonlinear dependence in the shocks, we draw an entire vector representing the same day for all the assets.
From this draw, we can compute a random return for day t + 1 as
Using the new simulated shock vector,  , we can update the volatilities and correlations using the GARCH models and the DCC model. We thus obtain simulated
, we can update the volatilities and correlations using the GARCH models and the DCC model. We thus obtain simulated  and
and  . Drawing a new vector of uncorrelated shocks,
. Drawing a new vector of uncorrelated shocks,  , enables us to simulate the return for the second day as
, enables us to simulate the return for the second day as
The advantages of the multivariate FHS approach tally with those of the univariate case: It captures current market conditions by means of dynamic variance and correlation models. It makes no assumption on the conditional multivariate shock distributions. And, it allows for the computation of any risk measure for any investment horizon of interest.
5. Summary
Risk managers rarely have one particular horizon of interest but rather want to know the risk profile across many different horizons; that is, the term structure of risk. The purpose of this chapter has therefore been to introduce Monte Carlo simulation and filtered Historical Simulation techniques, which can be used to compute the term structure of risk in the univariate risk models in Part II as well as in the multivariate risk models in Chapter 7. It is important to keep in mind that because we are simulating from dynamic risk models, we use all the relevant information available at any given time to compute the risk forecasts across future horizons.
Further Resources
Theoretical issues involved in temporal aggregation of GARCH models are analyzed in Drost and Nijman (1993). Diebold et al. (1998a) study the problems arising in risk management from simple scaling rules of variance across horizons. Christoffersen et al. (1998) elaborate on the issues involved in calculating VaR s at different horizons. Christoffersen and Diebold (2000) investigate the usefulness of dynamic variance models for risk management at various forecast horizons. Portfolio aggregation of GARCH models is analyzed in Zaffaroni (2007).
A thorough and current treatment of Monte Carlo methods in financial engineering can be found in the Glasserman (2004) book. Hammersley and Handscomb (1964) is the classic reference on Monte Carlo methods.
Diebold et al. (1998a); Hull and White (1998); and Barone-Adesi et al. (1999) independently suggested the filtered Historical Simulation approach. See also Barone-Adesi et al. (1998); and Barone-Adesi et al. (2002), who consider an application of FHS to portfolios of options and futures. Pritsker (2006) provides a powerful comparison between FHS and traditional Historical Simulation.
When constructing correlated random shocks, Patton and Sheppard (2009) recommend the spectral decomposition of the correlation matrix over the standard Cholesky decomposition because the latter is not invariant to the ordering of the assets in the vector of shocks.
Engle (2009) and Engle and Sheppard (2001) develop approximate formulas for correlation forecasts in DCC models. Asai and McAleer (2009) consider a stochastic correlation modeling approach.
Parametric alternatives to the Filtered Historical Simulation approach include specifying a multivariate normal or t distribution for the GARCH shocks. See, for example, Pesaran et al. (2009) as well as Chapter 9 in this book.
See Engle and Manganelli (2004) for a survey of different VaR modeling approaches. Manganelli (2004) considers a unique asset allocation approach that only requires a univariate model.
References
Asai, M.; McAleer, M., The structure of dynamic correlations in multivariate stochastic volatility models, J. Econom. 150 (2009) 182–192.
Barone-Adesi, G.; Bourgoin, F.; Giannopoulos, K., Don't look back, Risk 11 (August) (1998) 100–104.
Barone-Adesi, G.; Giannopoulos, K.; Vosper, L., VaR without correlations for non-linear portfolios, J. Futures Mark. 19 (1999) 583–602.
Barone-Adesi, G.; Giannopoulos, K.; Vosper, L., Backtesting derivative portfolios with filtered historical simulation (FHS), Eur. Financ. Manag. 8 (2002) 31–58.
Christoffersen, P.; Diebold, F., How relevant is volatility forecasting for financial risk management?Rev. Econ. Stat. 82 (2000) 1–11.
Christoffersen, P.; Diebold, F.; Schuermann, T., Horizon problems and extreme events in financial risk management, Fed. Reserve Bank New York Econ. Policy Rev. 4 (1998) 109–118.
Diebold, F.X.; Hickman, A.; Inoue, A.; Schuermann, T., Scale models, Risk 11 (1998) 104–107.
Drost, F.; Nijman, T., Temporal aggregation of GARCH processes, Econometrica 61 (1993) 909–927.
Engle, R., Anticipating Correlations: A New Paradigm for Risk Management. (2009) Princeton University Press, Princeton, NJ.
Engle, R.; Manganelli, S., A comparison of value at risk models in finance, In: (Editor: Szego, G.) Risk Measures for the 21st Century (2004) Wiley Finance, John Wiley Sons, Ltd., Chichester, West Sussex, England, pp. 123–144.
Engle, R.; Sheppard, K., Theoretical and empirical properties of dynamic conditional correlation multivariate GARCH, Available from: SSRN,http://ssrn.com/abstract=1296441 (2001).
Glasserman, P., Monte Carlo Methods in Financial Engineering. (2004) Springer Verlag.
Hammersley, J.; Handscomb, D., Monte Carlo Methods. (1964) Fletcher and Sons, Norwich, UK.
Hull, J.; White, A., Incorporating volatility updating into the historical simulation method for VaR, J. Risk 1 (1998) 5–19.
Manganelli, S., Asset allocation by variance sensitivity analysis, J. Financ. Econom. 2 (2004) 370–389.
Patton, A.; Sheppard, K., Evaluating volatility and correlation forecasts, In: (Editors: Andersen, T.G.; Davis, R.A.; Kreiss, J.-P.; Mikosch, T.) Handbook of Financial Time Series (2009) Springer Verlag, Berlin, pp. 801–838.
Pesaran, H.; Schleicher, C.; Zaffaroni, P., Model averaging in risk management with an application to futures markets, J. Empir. Finance 16 (2009) 280–305.
Pritsker, M., The hidden dangers of historical simulation, J. Bank. Finance 30 (2006) 561–582.
Zaffaroni, P., Aggregation and memory of models of changing volatility, J. Econom. 136 (2007) 237–249.
1. Construct the 10-day, 1% VaR on the last day of the sample using FHS (with 10,000 simulations), RiskMetrics scaling the daily VaR s by  (although it is incorrect), and Monte Carlo simulations of the NGARCH(1,1) model with normally distributed shocks and with parameters as estimated in Chapter 4.
(although it is incorrect), and Monte Carlo simulations of the NGARCH(1,1) model with normally distributed shocks and with parameters as estimated in Chapter 4.
2. Consider counterfactual scenarios where the volatility on the last day of the sample was three times its actual value and also one-half its actual value. Recompute the 10-day VaR in exercise 1. What do you see?
3. Repeat exercise 1 computing ES rather than VaR.
4. Using the DCC model estimated in Chapter 7 try to replicate the correlation forecasts in Figure 8.5, using 10,000 Monte Carlo simulations. Compared with Figure 8.5 do you find evidence of Monte Carlo estimation error when MC = 10,000?
The answers to these exercises can be found in the Chapter8Results.xlsx file. Which is available in the companion site.
For more information see the companion site at http://www.elsevierdirect.com/companions/9780123744487
..................Content has been hidden....................
You can't read the all page of ebook, please click here login for view all page.




