2. Historical Simulation, Value-at-Risk, and Expected Shortfall
This chapter introduces the most commonly used method for computing Value-at-Risk, namely Historical Simulation (HS), and discusses the pros and cons of this method. We also consider an extension of HS, referred to as Weighted Historical Simulation (WHS). We compare HS and WHS during the 1987 crash. We then study the performance of HS during the 2008–2009 financial crisis and compare it to the RiskMetrics alternative. The inherent problems with HS highlighted in this chapter serves to motivate the dynamic risk models considered later on in the book. The second part of the chapter discusses the pros and cons of the Value-at-Risk measure itself and considers the Expected Shortfall alternative.
Keywords: Historical Simulation, Value-at-Risk, Expected Shortfall.
1. Chapter Overview
The main objectives of this chapter are twofold. First we want to introduce the most commonly used method for computing VaR, Historical Simulation, and we discuss the pros and cons of this method. We then discuss the pros and cons of the VaR risk measure itself and consider the Expected Shortfall (ES) alternative.
The chapter is organized as follows:
• We introduce the Historical Simulation (HS) method and discuss its pros and particularly its cons.
• We consider an extension of HS, often referred to as Weighted Historical Simulation (WHS). We compare HS and WHS during the 1987 crash.
• We then study the performance of HS and RiskMetrics during the 2008–2009 financial crisis.
• We simulate artificial return data and assess the HS VaR on this data.
• Finally we compare the VaR risk measure with a potentially more informative alternative, ES.
The overall conclusion from this chapter is that HS is problematic for computing VaR. This will motivate the dynamic models considered later. These models can be used to compute Expected Shortfall or any other desired risk measure.
2. Historical Simulation
This section defines the HS approach to Value-at-Risk and then discusses the pros and cons of the approach.
2.1. Defining Historical Simulation
Let today be day t. Consider a portfolio of n assets. If we today own 
units or shares of asset i then the value of the portfolio today is
units or shares of asset i then the value of the portfolio today is
Using today's portfolio holdings but historical asset prices we can compute the history of “pseudo” portfolio values that would have materialized if today's portfolio allocation had been used through time. For example, yesterday's pseudo portfolio value is
Armed with this definition, we are now ready to define the Historical Simulation approach to risk management. The HS technique is deceptively simple. Consider the availability of a past sequence of m daily hypothetical portfolio returns, calculated using past prices of the underlying assets of the portfolio, but using today's portfolio weights; call it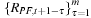 
.
.The HS technique simply assumes that the distribution of tomorrow's portfolio returns,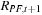 
, is well approximated by the empirical distribution of the past m observations, 
. Put differently, the distribution of 
is captured by the histogram of 
. The VaR with coverage rate, p, is then simply calculated as 100pth percentile of the sequence of past portfolio returns. We write
, is well approximated by the empirical distribution of the past m observations, . Put differently, the distribution of is captured by the histogram of . The VaR with coverage rate, p, is then simply calculated as 100pth percentile of the sequence of past portfolio returns. We write
Thus, we simply sort the returns in 
in ascending order and choose the 
to be the number such that only 100p% of the observations are smaller than the 
As the VaR typically falls in between two observations, linear interpolation can be used to calculate the exact number. Standard quantitative software packages will have the Percentile or similar functions built in so that the linear interpolation is performed automatically.
in ascending order and choose the to be the number such that only 100p% of the observations are smaller than the As the VaR typically falls in between two observations, linear interpolation can be used to calculate the exact number. Standard quantitative software packages will have the Percentile or similar functions built in so that the linear interpolation is performed automatically.2.2. Pros and Cons of Historical Simulation
Historical Simulation is widely used in practice. The main reasons are (1) the ease with which is it implemented and (2) its model-free nature.
The first advantage is difficult to argue with. The HS technique clearly is very easy to implement. No parameters have to be estimated by maximum likelihood or any other method. Therefore, no numerical optimization has to be performed.
The second advantage is more contentious, however. The HS technique is model-free in the sense that it does not rely on any particular parametric model such as a RiskMetrics model for variance and a normal distribution for the standardized returns. HS lets the past m data points speak fully about the distribution of tomorrow's return without imposing any further assumptions. Model-free approaches have the obvious advantage compared with model-based approaches that relying on a model can be misleading if the model is poor.
The model-free nature of the HS model also has serious drawbacks, however.
Consider the choice of the data sample length, m. How large should m be? If m is too large, then the most recent observations, which presumably are the most relevant for tomorrow's distribution, will carry very little weight, and the VaR will tend to look very smooth over time. If m is chosen to be too small, then the sample may not include enough large losses to enable the risk manager to calculate, say, a 1% VaR with any precision. Conversely, the most recent past may be very unusual, so that tomorrow's VaR will be too extreme. The upshot is that the choice of m is very ad hoc, and, unfortunately, the particular choice of m matters a lot for the magnitude and dynamics of VaR from the HS technique. Typically m is chosen in practice to be between 250 and 1000 days corresponding to approximately 1 to 4 years. Figure 2.1 shows VaRs from HS m = 250 and m = 1000, respectively, using daily returns on the S&P 500 for July 1, 2008 through December 31, 2009. Notice the curious box-shaped patterns that arise from the abrupt inclusion and exclusion of large losses in the moving sample. Notice also how the dynamic patterns of the HS VaRs are crucially dependent on m. The 250-day HS VaR is almost twice as high as the 1000-day VaR during the crisis period. Furthermore, the 250-day VaR rises quicker at the beginning of the crisis and it drops quicker as well at the end of the crisis. The key question is whether the HS VaR rises quickly enough and to the appropriate level.
 |
| Figure 2.1 |
The lack of properly specified dynamics in the HS methodology causes it to ignore well-established stylized facts on return dependence, most importantly variance clustering. This typically causes the HS VaR to react too slowly to changes in the market risk environment. We will consider a stark example of this next.
Because a reasonably large m is needed in order to calculate 1% VaRs with any degree of precision, the HS technique has a serious drawback when it comes to calculating the VaR for the next, say, 10 days rather than the next day. Ideally, the 10-day VaR should be calculated from 10-day nonoverlapping past returns, which would entail coming up with 10 times as many past daily returns. This is often not feasible. Thus, the model-free advantage of the HS technique is simultaneously a serious drawback. As the HS method does not rely on a well-specified dynamic model, we have no theoretically correct way of extrapolating from the 1-day distribution to get the 10-day distribution other than finding more past data. While it may be tempting to simply multiply the 1-day VaR from HS by 
to obtain a 10-day VaR, doing so is only valid under the assumption of normality, which the HS approach is explicitly tailored to avoid.
to obtain a 10-day VaR, doing so is only valid under the assumption of normality, which the HS approach is explicitly tailored to avoid.In contrast, the dynamic return models suggested later in the book can be generalized to provide return distributions at any horizon. We will consider methods to do so in Chapter 8.
3. Weighted Historical Simulation (WHS)
We have discussed the inherent tension in the HS approach regarding the choice of sample size, m. If m is too small, then we do not have enough observations in the left tail to calculate a precise VaR measure, and if m is too large, then the VaR will not be sufficiently responsive to the most recent returns, which presumably have the most information about tomorrow's distribution.
We now consider a modification of the HS technique, which is designed to relieve the tension in the choice of m by assigning relatively more weight to the most recent observations and relatively less weight to the returns further in the past. This technique is referred to as Weighted Historical Simulation (WHS).
WHS is implemented as follows:
• Our sample of m past hypothetical returns, 
, is assigned probability weights declining exponentially through the past as follows:
, is assigned probability weights declining exponentially through the past as follows:
Note that 
goes to zero as τ gets large, and that the weights 
for τ = 1, 2.., m sum to 1.Typically, η is assumed to be a number between 0.95 and 0.99.
• The 100p% VaR is calculated by accumulating the weights of the ascending returns until 100p% is reached. Again, linear interpolation can be used to calculate the exact VaR number between the two sorted returns with cumulative probability weights surrounding p.
Notice that once η is chosen, the WHS technique still does not require estimation and thus retains the ease of implementation, which is the hallmark of simple HS. It has the added advantage that the weighting function builds dynamics into the technique: Today's market conditions matter more because today's return gets weighted much more than past returns. The weighting function also makes the choice of m somewhat less crucial.
An obvious downside of the WHS approach is that no guidance is given on how to choose η. A more subtle, but also much more important downside is the effect on the weighting scheme of positive versus negative past returns—a downside that WHS shares with HS. We illustrate this with a somewhat extreme example drawing on the month surrounding the October 19, 1987, crash in the stock market. Figure 2.2 contains two panels both showing in blue lines the daily losses on a portfolio consisting of a $1 long position in the S&P 500 index. Notice how the returns are relatively calm before October 19, when a more than 20% loss from the crash set off a dramatic increase in market variance.
The blue line in the top panel shows the VaR from the simple HS technique, using an m of 250. The key thing to notice of course is how the simple HS technique responds slowly and relatively little to the dramatic loss on October 19. The HS's lack of response to the crash is due to its static nature: Once the crash occurs, it simply becomes another observation in the sample that carries the same weight as the other 250 past observations. The VaR from the WHS method in the bottom panel (shown in red) shows a much more rapid and large response to the VaR forecast from the crash. As soon as the large portfolio loss from the crash is recorded, it gets assigned a large weight in the weighting scheme, which in turn increases the VaR dramatically. The WHS VaRs in Figure 2.2 assume a η of 0.99.
Thus, apparently the WHS performs its task sublimely. The dynamics of the weighting scheme kicks in to lower the VaR exactly when our intuition says it should. Unfortunately, all is not well. Consider Figure 2.3, which in both panels shows the daily losses from a short $1 position in the S&P 500 index. Thus, we have simply flipped the losses from before around the x-axis. The top panel shows the VaR from HS, which is even more sluggish than before: Since we are short the S&P 500, the market crash corresponds to a large gain rather than a large loss. Consequently, it has no impact on the VaR, which is calculated from the largest losses only. Consider now the WHS VaR instead. The bottom panel of Figure 2.3 shows that as we are short the market, the October 19 crash has no impact on our VaR, only the subsequent market rebound, which corresponds to a loss for us, increases the VaR.
Thus, the upshot is that while WHS responds quickly to large losses, it does not respond to large gains. Arguably it should. The market crash sets off an increase in market variance, which the WHS only picks up if the crash is bad for our portfolio position. To put it bluntly, the WHS treats a large loss as a signal that risk has increased, but a large gain is chalked up to the portfolio managers being clever. This is not a prudent risk management approach.
Notice that the RiskMetrics model would have picked up the increase in market variance from the crash regardless of whether the crash meant a gain or a loss to us. In the RiskMetrics model, returns are squared and losses and gains are treated as having the same impact on tomorrow's variance and therefore on the portfolio risk.
Finally, a serious downside of WHS, and one it shares with the simple HS approach, is that the multiday Value-at-Risk requires a large amount of past daily return data, which is often not easy to obtain. We will study multiperiod risk modeling in Chapter 8.
4. Evidence from the 2008–2009 Crisis
The 1987 crash provides a particularly dramatic example of the problems embedded in the HS approach to VaR computation. The recent financial crisis involved different market dynamics than the 1987 crash but the implications for HS VaR are equally serious in the recent example.
Figure 2.4 shows the daily closing prices for a total return index (that is including dividends) of the S&P 500 starting in July 2008 and ending in December 2009. The index lost almost half its value between July 2008 and the market bottom in March 2009. The recovery in the index starting in March 2009 continued through the end of 2009.
 |
| Figure 2.4 |
HS again provides a simple way to compute VaR, and the red line in Figure 2.5 shows the 10-day, 1% HS VaR. As is standard, the 10-day VaR is computed from the 1-day VaR by simply multiplying it by 
:
:
to get the 10-day VaR. We have assumed a standard normal distribution for the return innovation so that the percentile is easily computed as 
. |
| Figure 2.5 |
Notice the dramatic difference between the HS and the RM VaRs in Figure 2.5. The HS VaR rises much more slowly as the crisis gets underway in the fall of 2008 and perhaps even more strikingly, the HS VaR stays at its highest point for almost a year during which the volatility in the market has declined considerably. The units in Figure 2.5 refer to the least percent of capital that would be lost over the next 10 days in the 1% worst outcomes.
The upshot is that a risk management team that relies on HS VaR will detect the brewing crisis quite slowly and furthermore will enforce excessive caution after volatility drops in the market.
In order to put some dollar figures on this effect Figure 2.6 conducts the following experiment. Assume that each day a trader has a 10-day, 1% dollar VaR limit of $100,000. Each day he or she is therefore allowed to invest
Let us assume that the trader each day simply invests the maximum amount possible in the S&P 500, that is
The difference in performance is quite striking. The RM trader will lose less in the fall of 2008 and earn much more in 2009. The HS trader takes more dramatic losses in the fall of 2008 and is not allowed to invest sufficiently in the market in 2009 to take advantage of the run-up in the index. The HS VaR reacts too slowly to increases in volatility as well as to decreases in volatility. Both errors are potentially very costly.
The RM risk model is very simple—potentially too simple in several respects, which will be discussed in Chapter 4, Chapter 6 and Chapter 8. Important extensions to the simple variance dynamic assumed in RiskMetrics will be discussed in detail in Chapter 4. Recall also that we have assumed a standard normal distribution for the return innovation. This assumption is just made for convenience at this point. In Chapter 6 we will discuss ways to improve the risk model by allowing for nonnormal return innovations. Finally, we simply scaled the 1-day VaR by 
to get the 10-day VaR. This simple rule is an approximation that is often not accurate. It will be discussed in detail in Chapter 8.
to get the 10-day VaR. This simple rule is an approximation that is often not accurate. It will be discussed in detail in Chapter 8.5. The True Probability of Breaching the HS VaR
The 1987 and the 2008–2009 examples indicated the problems inherent in the HS approach but they could be dismissed as being just examples and of course not randomly chosen periods. In order to get beyond these concerns we now conduct the following purely artificial but revealing experiment.
Assume that the S&P 500 market returns are generated by a time series process with dynamic volatility and normal innovations. In reality of course they are not but if we make this radically simplifying assumption then we are able to compute how wrong the HS VaR can get. To be specific, assume that innovation to S&P 500 returns each day is drawn from the normal distribution with mean zero and variance equal to 
, which is generated by a GARCH type variance process that we will introduce in Chapter 4. We can write
, which is generated by a GARCH type variance process that we will introduce in Chapter 4. We can write
If we simulate 1,250 return observations from this process, then starting on day 251 we can, on each day, compute the 1-day, 1% VaR using Historical Simulation. Because we know how the returns were created, we can, on each day, compute the true probability that we will observe a loss larger than the HS VaR we have computed. We call this the probability of a VaR breach. It is computed as
is again the cumulative density function for a standard normal random variable. Figure 2.7 shows this probability over the 1,000 simulated return days. |
| Figure 2.7 |
If the HS VaR model had been accurate then this plot should show a roughly flat line at 1%. Instead we see numbers as high as 16%, which happens when volatility is high, and numbers very close to 0%, which happens when volatility is low. The HS VaR will tend to overestimate risk when the true market volatility is low, which will generate a low probability of a VaR breach in Figure 2.7. Conversely, and more crucially, HS will underestimate risk when true volatility is high in which case the VaR breach volatility will be high. The HS approach, which is supposed to deliver a 1% VaR, sometimes delivers a 16% VaR, which means that there is roughly a 1 in 6 chance of getting a loss worse than the HS VaR, when there is supposed to be only a 1 in 100 chance. The upshot is that HS VaR may be roughly correct on average (the average of the probabilities in Figure 2.7 is 2.3%) but the HS VaR is much too low when volatility is high and the HS VaR is too high when volatility is low.
This example has used Monte Carlo simulation to generate artificial returns. We will study the details of Monte Carlo simulation in Chapter 8.
6. VaR with Extreme Coverage Rates
The most complete picture of risk is no doubt provided by reporting the entire shape of the tail of the distribution of losses beyond the VaR. The tail of the portfolio return distribution, when modeled correctly, tells the risk manager everything about the future losses. Reporting the entire tail of the return distribution corresponds to reporting VaRs for many different coverage rates, say p ranging from 0.01% to 2.5% in increments. Note that when using HS with a 250-day sample it is not even possible to compute the VaR when 
.
.Figure 2.8 illustrates the relative difference between a VaR from a nonnormal distribution (with an excess kurtosis of 3) and a VaR from a normal distribution as a function of the VaR probability, p. Notice that as p gets close to zero (the smallest p in the figure is 0.0001, which is 0.01%) the nonnormal VaR gets much larger than the normal VaR. Strikingly, when p = 0.025 (i.e., 2.5%) there is almost no difference between the two VaRs even though the underlying distributions are actually quite different as the VaRs with extreme p s show. Relying on VaR with large p is dangerous because extreme risks are hidden. Chapter 6 will detail the important task of modeling nonnormality in the return distribution.
 |
| Figure 2.8 |
The popularity of VaR as a risk measurement tool is due to its simple interpretation: “What's the loss so that only 100p% of potential losses tomorrow will be worse?” However, reporting the VaR for several values of p, where p is small, should be given serious consideration in risk reporting as it maps out the tail of the loss distribution.
7. Expected Shortfall
We previously discussed a key shortcoming of VaR, namely that it is concerned only with the percentage of losses that exceed the VaR and not the magnitude of these losses. The magnitude, however, should be of serious concern to the risk manager. Extremely large losses are of course much more likely to cause financial distress, such as bankruptcy, than are moderately large losses; therefore we want to consider a risk measure that accounts for the magnitude of large losses as well as their probability of occurring.
The challenge is to come up with a portfolio risk measure that retains the simplicity of the VaR, but conveys information regarding the shape of the tail. Expected Shortfall (ES), or TailVaR as it is sometimes called, is one way to do this.
Mathematically ES is defined as
The distribution tail gives us information on the range of possible extreme losses and the probability associated with each outcome. The Expected Shortfall measure aggregates this information into a single number by computing the average of the tail outcomes weighted by their probabilities. So where VaR tells us the loss so that only 1% of potential losses will be worse, the ES tells us the expected loss given that we actually get a loss from the 1% tail. So while we are not conveying all the information in the shape of the tail when using ES, the key is that the shape of the tail beyond the VaR measure is now important for determining the risk number.
To gain more insight into the ES as a risk measure, let's first consider the normal distribution. In order to compute ES we need the distribution of a normal variable conditional on it being below the VaR. The truncated standard normal distribution is defined from the standard normal distribution as
denotes the density function and 
the cumulative density function of the standard normal distribution.Recall that 
. In the normal distribution case ES can therefore be derived as
. In the normal distribution case ES can therefore be derived as
The relative difference between ES and VaR is
, and the relative difference is then
From this it would seem that it really doesn't matter much whether the risk manager uses VaR or ES as a risk measure. The difference is only 15% when the VaR coverage rate is 1%. Recall, however, that we argued in Chapter 1 that normal distributions fit asset return data poorly, particularly in the tail. So what happens to the 
ratio when we look at nonnormal distributions?
ratio when we look at nonnormal distributions?Figure 2.9 considers a fat-tailed distribution where the degree of fatness in the tail is captured by excess kurtosis as defined in Chapter 1: the higher the excess kurtosis the fatter the distribution tail. The blue line in Figure 2.9 covers the case where p = 1% and the red line shows p = 5%.
 |
| Figure 2.9 |
The blue line shows that when excess kurtosis is zero we get that the relative difference between the ES and VaR is 15%, which matches the preceding computation for the normal distribution. The blue line in Figure 2.9 also shows that for moderately large values of excess kurtosis, the relative difference between ES and VaR is above 30%.
Comparing the red line with the blue line in Figure 2.9 it is clear that the relative difference between VaR and ES is larger when p is larger and thus further from zero. When p is close to zero VaR and ES will both capture the fat tails in the distribution. When p is far from zero, only the ES will capture the fat tails in the return distribution. When using VaR and a large p the dangerous large losses will be hidden from view. Generally an ES-based risk measure will be better able to capture the fact that a portfolio with large kurtosis (or negative skewness) is more risky than a portfolio with low kurtosis.
Risk managers who rely on Historical Simulation often report VaR with relatively large p because they are worried about basing the VaR estimate on too few observations. Figure 2.9 indirectly shows that this argument has a serious downside: The larger the p the more likely it is that extreme risks (evident in ES) in the portfolio return distribution will go unnoticed in the VaR. The ES risk measure will capture such extreme risks. The VaR will not.
8. Summary
VaR is the most popular risk measure in use and HS is the most often used methodology to compute VaR. This chapter has argued that VaR as commonly reported has some shortcomings and that using HS to compute VaR has serious problems as well.
We need instead to use risk measures that capture the degree of fatness in the tail of the return distribution, and we need risk models that properly account for the dynamics in variance and models that can be used across different return horizons.
Going forward the goal will be to develop risk models with the following characteristics:
• The model is a fully specified statistical process that can be estimated on daily returns.
• The model can be estimated and implemented for portfolios with a large number of assets.
• VaR and ES can be easily computed for any prespecified level of confidence, p, and for any horizon of interest, K.
• VaR and ES are dynamic reflecting current market conditions.
In order to deliver accurate risk predictions, the model should reflect the following stylized facts of daily asset returns discussed in Chapter 1:
• The expected daily returns have little or no predictability.
• The variance of daily returns greatly exceeds the mean.
• The variance of daily returns is predictable.
• Daily returns are not normally distributed.
• Even after standardizing daily returns by a dynamic variance model, the standardized daily returns are not normally distributed.
• Positive and negative returns of the same magnitude may have different impacts on the variance.
• Correlations between assets appear to be time-varying.
• As the investment horizon increases, the return data distribution approaches the normal distribution.
Further Resources
Useful overviews of the various approaches to VaR calculation can be found in Duffie and Pan (1997), Engle and Manganelli (2004a), Jorion (2006) and Christoffersen (2009).
Dowd and Blake (2006) discuss the use of VaR-like measures in the insurance industry. Danielsson (2002) warns against using risk models estimated on asset return data from calm markets.
Bodoukh et al. (1998) introduced the Weighted Historical Simulation approach. They found that it compares favorably with both the HS approach and the RiskMetrics model. Figure 2.2 and Figure 2.3 are based on Pritsker (2006).
Engle and Manganelli (2004b) suggest an interesting alternative method (not discussed in this chapter) for VaR calculation based on conditional quantile regression.
Artzner et al. (1999) define the concept of a coherent risk measure and showed that Expected Shortfall (ES) is coherent whereas VaR is not. Inui and Kijima (2005) provide additional theoretical arguments for the use of ES. Taylor (2008) provides econometric tools for ES computation.
Studying dynamic portfolio management based on ES and VaR, Basak and Shapiro (2001) found that when a large loss does occur, ES risk management leads to lower losses than VaR risk management. Cuoco et al. (2008) argued instead that VaR and ES risk management lead to equivalent results as long as the VaR and ES risk measures are recalculated often. Both Basak and Shapiro (2001) and Cuoco et al. (2008) assumed that returns are normally distributed. Yamai and Yoshiba (2005) compare VaR and ES from a practical perspective. Berkowitz and O'Brien (2002) and Alexander and Baptista (2006) look at VaR from a regulatory perspective.
Alexander, G.J.; Baptista, A.M., Does the Basle Capital Accord reduce bank fragility? An assessment of the Value-at-Risk approach., J. Monet. Econom. 53 (2006) 1631–1660.
Artzner, P.; Delbaen, F.; Eber, J.; Heath, D., Coherent measures of risk, Math. Finance 9 (1999) 203–228.
Basak, S.; Shapiro, A., Value-at-risk-based risk management: Optimal policies and asset prices, Rev. Financial Stud. 14 (2001) 371–405.
Berkowitz, J.; O'Brien, J., How accurate are Value-at-Risk models at commercial banks?J. Finance 57 (2002) 1093–1111.
Bodoukh, J.; Richardson, M.; Whitelaw, R., The best of both worlds, Risk 11 (1998) 64–67.
Christoffersen, P., Value-at-Risk models, In: (Editors: Mikosch, T.; Kreib, J.-P.; Davis, R.A.; Andersen, T.G.) Handbook of Financial Time Series (2009) Springer Verlag, Berlin, pp. 753–766.
Cuoco, D.; He, H.; Issaenko, S., Optimal dynamic trading strategies with risk limits, Oper. Res. 56 (2008) 358–368.
Danielsson, J., The emperor has no clothes: Limits to risk modelling, J. Bank. Finance 26 (2002) 1273–1296.
Dowd, K.; Blake, D., After VaR: The theory, estimation, and insurance applications of quantile-based risk measures, J. Risk Insur. 73 (2006) 193–229.
Duffie, D.; Pan, J., An overview of value at risk, J. Derivatives 4 (1997) 7–49.
Engle, R.; Manganelli, S., A comparison of value at risk models in finance, In: (Editor: Szego, Giorgio) Risk Measures for the 21st Century (2004) Wiley Finance, West Sussex England.
Engle, R.; Manganelli, S., CAViaR: Conditional value at risk by quantile regression, J. Bus. Econom. Stat. 22 (2004) 367–381.
Inui, K.; Kijima, M., On the significance of expected shortfall as a coherent risk measure, J. Bank. Finance 29 (2005) 853–864.
Jorion, P., Value-at-Risk: The New Benchmark for Managing Financial Risk. third ed (2006) McGraw-Hill, New York, NY.
Pritsker, M., The hidden dangers of historical simulation, J. Bank. Finance 30 (2006) 561–582.
Taylor, J.W., Estimating value at risk and expected shortfall using expectiles, J. Financial Econom. 6 (2008) 231–252.
Yamai, Y.; Yoshiba, T., Value-at-Risk versus expected shortfall: A practical perspective, J. Bank. Finance 29 (2005) 997–1015.
Open the Chapter2data.xlsx file on the web site. Use sheet 1 for questions 1 and 2, and sheet 2 for questions 3 and 4.
Assume you are long $1 of the S&P 500 index on each day. Calculate the 1-day, 1% VaRs on each day in October 1987 using Historical Simulation. Use a 250-day moving window. Plot the VaR and the losses. Repeat the exercise assuming you are short $1 each day. Plot the VaR and the losses again. Compare with Figure 2.2 and Figure 2.3.
Assume you are long $1 of the S&P 500 index on each day. Calculate the 1-day, 1% VaRs on each day in October 1987 using Weighted Historical Simulation. You can ignore the linear interpolation part of WHS. Use a weighting parameter of η = 0.99 in WHS. Use a 250-day moving window. ( Excel hint: Sort the returns along with their weights by selecting both columns in Excel and sorting by returns.) Repeat the exercise assuming you are short $1 each day. Plot the VaR and the losses again. Compare with Figure 2.2 and Figure 2.3.
For each day from July 1, 2008 through December 31, 2009, calculate the 10-day, 1% VaRs using the following methods: (a) RiskMetrics, that is, normal distribution with an exponential smoother on variance using the weight, λ = 0.94; and (b) Historical Simulation. Use a 250-day moving sample. Compute the 10-day VaRs from the 1-day VaRs by just multiplying by square root of 10. Plot the VaR s.
Reconstruct the P/Ls in Figure 2.6.
The answers to these exercises can be found in the Chapter2Results.xlsx file on the companion website.
For more information see the companion site at http://www.elsevierdirect.com/companions/9780123744487
..................Content has been hidden....................
You can't read the all page of ebook, please click here login for view all page.