10. Option Pricing
This chapter is devoted to the pricing of options. An option derives its value from an underlying asset, but its payoff is a nonlinear function of the underlying asset price, and so the option price is also a nonlinear function of the underlying asset price. This nonlinearity adds complications to pricing and risk management. In this chapter we will first introduce the binomial tree approach and the Black-Scholes-Merton (BSM) approach to option pricing. We then extend the BSM model by allowing for skewness and kurtosis in returns as well as for time-varying volatility. We will also introduce the ad hoc implied volatility function (IVF) approach to option pricing. The IVF method is not derived from any coherent theory but it works well in practice.
Keywords: Binomial trees, Black-Scholes-Merton model, Gram-Charlier approximation, implied volatility functions.
1. Chapter Overview
The previous chapters have established a framework for constructing the distribution of a portfolio of assets with simple linear payoffs—for example, stocks, bonds, foreign exchange, forwards, futures, and commodities. This chapter is devoted to the pricing of options. An option derives its value from an underlying asset, but its payoff is not a linear function of the underlying asset price, and so the option price is not a linear function of the underlying asset price either. This nonlinearity adds complications to pricing and risk management.
In this chapter we will do the following:
• Provide some basic definitions and derive a no-arbitrage relationship between put and call prices on the same underlying asset.
• Briefly summarize the binomial tree approach to option pricing.
• Establish an option pricing formula under the simplistic assumption that daily returns on the underlying asset follow a normal distribution with constant variance. We will refer to this as the Black-Scholes-Merton (BSM) formula. While the BSM model provides a useful benchmark, it systematically misprices observed options. We therefore consider the following alternatives.
• Extend the normal distribution model by allowing for skewness and kurtosis in returns. We will rely on the Gram-Charlier expansion around the normal distribution to derive an option pricing formula in this case.
• Extend the model by allowing for time-varying variance relying on the GARCH models from Chapter 4. Two GARCH option pricing models are considered: one allows for general variance specifications, but requires Monte Carlo simulation or another numerical technique; the other assumes a specific variance dynamic but provides a closed-form solution for the option price.
• Introduce the ad hoc implied volatility function (IVF) approach to option pricing. The IVF method is not derived from any coherent theory but it works well in practice.
In this chapter, we will mainly focus attention on the pricing of European options, which can only be exercised on the maturity date. American options that can be exercised early will only be discussed briefly. The following chapter will describe in detail the risk management techniques available when the portfolio contains options.
There is enough material in this chapter to fill an entire book, so needless to say the discussion will be brief. We will simply provide an overview of different available option pricing models and suggest further readings at the end of the chapter.
2. Basic Definitions
A European call option gives the owner the right but not the obligation (that is, it gives the option) to buy a unit of the underlying asset  days from now at the price X. We refer to
days from now at the price X. We refer to  as the days to maturity and X as the strike price of the option. We denote the price of the European call option today by c, the price of the underlying asset today by
as the days to maturity and X as the strike price of the option. We denote the price of the European call option today by c, the price of the underlying asset today by  and at maturity of the option by
and at maturity of the option by  .
.
A European put option gives the owner of the option the right to sell a unit of the underlying asset  days from now at the price X. We denote the price of the European put option today by p. The European option restricts the owner from exercising the option before the maturity date. American options can be exercised any time before the maturity date.
days from now at the price X. We denote the price of the European put option today by p. The European option restricts the owner from exercising the option before the maturity date. American options can be exercised any time before the maturity date.
We note that the number of days to maturity,  , is counted in calendar days and not in trading days. A standard year of course has 365 calendar days but only around 252 trading days. In previous chapters, we have been using trading days for returns and Value-at-Risk (VaR) horizons, for example, referring to a two-week VaR as a 10-day VaR. In this chapter it is therefore important to note that we are using 365 days per year when calculating volatilities and interest rates.
, is counted in calendar days and not in trading days. A standard year of course has 365 calendar days but only around 252 trading days. In previous chapters, we have been using trading days for returns and Value-at-Risk (VaR) horizons, for example, referring to a two-week VaR as a 10-day VaR. In this chapter it is therefore important to note that we are using 365 days per year when calculating volatilities and interest rates.
The payoff function is the option's defining characteristic. Figure 10.1 contains four panels. The top-left panel shows the payoff from a call option and the top-right panel shows the payoff of a put option both with a strike price of 1137. The payoffs are drawn as a function of the hypothetical price of the underlying asset at maturity of the option,  Mathematically, the payoff function for a call option is
Mathematically, the payoff function for a call option is
We next consider the relationship between European call and put option prices. Put-call parity does not rely on any particular option pricing model. It states
| Time t | Time | |
|---|---|---|
| Portfolio I | If | If |
| p | 0 | |
| X | ||
| Portfolio II | If | If |
| c | 0 | |
| X | X | |
| X | ||
The put-call parity also suggests how options can be used in risk management. Suppose an investor who has an investment horizon of  days owns a stock with current value St. The value of the stock at the maturity of the option is
days owns a stock with current value St. The value of the stock at the maturity of the option is  , which in the worst case could be zero. But an investor who owns the stock along with a put option with a strike price of X is guaranteed the future portfolio value
, which in the worst case could be zero. But an investor who owns the stock along with a put option with a strike price of X is guaranteed the future portfolio value  which is at least X. The downside of the stock portfolio including this so-called protective put is thus limited, whereas the upside is still unlimited. The protection is not free however as buying the put option requires paying the current put option price or premium, p.
which is at least X. The downside of the stock portfolio including this so-called protective put is thus limited, whereas the upside is still unlimited. The protection is not free however as buying the put option requires paying the current put option price or premium, p.
3. Option Pricing Using Binomial Trees
The key challenge we face when wanting to find a fair value of an option is that it depends on the distribution of the future price of the underlying risky asset (the stock). We begin by making the simplest possible assumption about this distribution, namely that it is binomial. This means that in a short interval of time, the stock price can only take on one of two values, which we can think of as up and down. Clearly this is the simplest possible assumption we can make: If the stock could only take on one possible value going forward then it would not be risky at all. While simple, the binomial tree approach is able to compute the fair market value of American options, which are complicated because early exercise is possible.
The binomial tree option pricing method will be illustrated using the following example: We want to find the fair value of a call and a put option with three months to maturity and a strike price of $900. The current price of the underlying stock is $1,000 and the volatility of the log return on the stock is 0.60 or 60% per year corresponding to  per calendar day.
per calendar day.
3.1. Step 1: Build the Tree for the Stock Price
We first must model the distribution of the stock price. The binomial model assumes that the stock price can only take on one of two values at the end of each period. This simple assumption enables us to map out exactly all the possible future values of the stock price. In our example we will assume that the tree has two steps during the six-month maturity of the option, but in practice, a hundred or so steps will be used. The more steps we use, the more accurate the model price will be, but of course the computational burden will increase as well.
Table 10.1 shows how the tree is built in Excel. We know that today's stock price is  and so we know the starting point of the tree. We also know the volatility of the underlying stock return (60% per year) and so we know the magnitude of a typical move in the stock price. We need to make sure that the tree accurately reflects the 60% stock return volatility per year.
and so we know the starting point of the tree. We also know the volatility of the underlying stock return (60% per year) and so we know the magnitude of a typical move in the stock price. We need to make sure that the tree accurately reflects the 60% stock return volatility per year.
If the option has three months to maturity and we are building a tree with two steps then each step in the tree corresponds to 1.5 months. The magnitude of the up and down move in each step should therefore reflect a volatility of 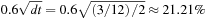 . In this equation dt denotes the length (in years) of a step in the tree. If we had measured volatility in days then dt should be measured in days as well.
. In this equation dt denotes the length (in years) of a step in the tree. If we had measured volatility in days then dt should be measured in days as well.
Using these up and down factors the tree is built from the current price of  on the left side to three potential values in three months, namely
on the left side to three potential values in three months, namely  if the stock price moves up twice,
if the stock price moves up twice,  if it has one up and one down move, and
if it has one up and one down move, and  if it moves down twice.
if it moves down twice.
3.2. Step 2: Compute the Option Payoff at Maturity
Once we have constructed the tree for the stock price we have three hypothetical stock price values at maturity and we can easily compute the hypothetical call option at each one. The value of an option at maturity is just the payoff stated in the option contract. For a call option we have the payoff function from before:

For the put option we have in general the payoff function

Table 10.2 shows the three terminal values of the call and put option in the right side of the tree.
The call option values are shown in green font and the put option values are shown in red font.
3.3. Step 3: Work Backward in the Tree to Get the Current Option Value
In the tree we have two possible stock price values 1.5 months from now:  at B and
at B and  at C. The challenge now is to compute a fair value of the option corresponding to these two stock prices. Consider first point B. We know that going forward from B the stock can only move to either D or E. We know the stock prices at these two points. We also know the option prices at D and E. We need one more piece of information, namely the return on a risk-free bond with 1.5 months to maturity, which corresponds to the length of a step in the tree. The term structure of government debt can be used to obtain this information. Let us assume that the term structure of interest rates is flat at 5% per year.
at C. The challenge now is to compute a fair value of the option corresponding to these two stock prices. Consider first point B. We know that going forward from B the stock can only move to either D or E. We know the stock prices at these two points. We also know the option prices at D and E. We need one more piece of information, namely the return on a risk-free bond with 1.5 months to maturity, which corresponds to the length of a step in the tree. The term structure of government debt can be used to obtain this information. Let us assume that the term structure of interest rates is flat at 5% per year.
The key insight is that in a binomial tree we are able to construct a risk-free portfolio using the stock and the option. Because it is risk-free such a portfolio must earn exactly the risk-free rate, which is 5% per year in our example. Consider a portfolio of −1 call option and ΔB shares of the stock. This means that we have sold one call option and we have bought ΔB shares of the stock. We need to find a ΔB such that the portfolio of the option and the stock is risk-free. A portfolio is risk-free if it pays exactly the same in any future state of the world. In our simple binomial world there are only two future states at the end of each step: up and down. Constructing a risk-free portfolio is therefore incredibly simple. Starting from point B we need to find a ΔB so that
This shows that we must hold one stock along with the short position of one option in order for the portfolio to be risk-free. The value of this portfolio at D (or E) is $900 and the portfolio value at B is the discounted value using the risk-free rate for 1.5 months, which is
Now that we have the option prices at points B and C we can construct a risk-free portfolio again to get the option price at point A. We get
3.4. Risk Neutral Valuation
Earlier we priced options based on no-arbitrage arguments: We have constructed a risk-free portfolio that in the absence of arbitrage must earn exactly the risk-free rate. From this portfolio we can back out European option prices. For example, for a call option at point B we used the formula
Using the ΔB formula we can rewrite the  formula as
formula as
In our example  ,
,  , and
, and  , so that
, so that
We can use this number to check that the new formula works. We get

The new formula can be used at any point in the tree. For example at point A we have
3.5. Pricing an American Option Using the Binomial Tree
American-style options can be exercised prior to maturity. This added flexibility gives them potentially higher fair market values than European-style options. Fortunately, binomial trees can be used to price American-style options also. We only have to add one calculation in the tree: At the maturity of the option American- and European-style options are equivalent. But at each intermediate point in the tree we must compare the European option value (also known as the continuation value) with the early exercise value and put the largest of the two into the tree at that point.
Consider Table 10.4 where we are pricing an American option that has a strike price of 1,100 but otherwise is exactly the same as the European option considered in Table 10.1, Table 10.2 and Table 10.3.
The American call option price is $90.25, which turns out to be the European call option price as well. This is because American call stock options should only be exercised early if a large cash dividend is imminent. In our example there were no dividends and so early exercise of the American call is never optimal, which in turn makes the American call option price equal to the European call option price.
3.6. Dividend Flows, Foreign Exchange, and Futures Options
In the case where the underlying asset pays out a stream of dividends or other cash flows we need to adjust the RNP formula. Consider an underlying stock index that pays out cash at a rate of q per year. In this case we have
When the underlying asset is a foreign exchange rate then q is set to the interest rate of the foreign currency. When the underlying asset is a futures contract then  so that
so that  for futures options.
for futures options.
4. Option Pricing under the Normal Distribution
The binomial tree approach is very useful because it is so simple to derive and because it allows us to price American as well as European options. A downside of binomial tree pricing is that we do not obtain a closed-form formula for the option price.
In order to do so we now assume that daily returns on an asset be independently and identically distributed according to the normal distribution,
The risk-neutral valuation principle calculates the option price as the discounted expected payoff, where discounting is done using the risk-free rate and where the expectation is taken using the risk-neutral distribution:


Black, Scholes, and Merton derived this pricing formula in the early 1970s using a model where trading takes place in continuous time when assuming continuous trading only the absence of arbitrage opportunities is needed to derive the formula.
It is worth emphasizing that to stay consistent with the rest of the book, the volatility and risk-free interest rates are both denoted in daily terms, and option maturity is denoted in number of calendar days, as this is market convention.
The elements in the option pricing formula have the following interpretation:
•  is the risk-neutral probability of exercise.
is the risk-neutral probability of exercise.
•  is the expected risk-neutral payout when exercising.
is the expected risk-neutral payout when exercising.
•  is the risk-neutral expected value of the stock acquired through exercise of the option.
is the risk-neutral expected value of the stock acquired through exercise of the option.
•  measures the sensitivity of the option price to changes in the underlying asset price,
measures the sensitivity of the option price to changes in the underlying asset price,  , and is referred to as the delta of the option, where
, and is referred to as the delta of the option, where  is the first derivative of the option with respect to the underlying asset price. This and other sensitivity measures are discussed in detail in the next chapter.
is the first derivative of the option with respect to the underlying asset price. This and other sensitivity measures are discussed in detail in the next chapter.

In the case where cash flows such as dividends accrue to the underlying asset, we discount the current asset price to account for the cash flows by replacing  by
by  everywhere, where q is the expected rate of cash flow per day until maturity of the option. This adjustment can be made to both the call and the put price formula, and in both cases the formula for d will then be
everywhere, where q is the expected rate of cash flow per day until maturity of the option. This adjustment can be made to both the call and the put price formula, and in both cases the formula for d will then be
The adjustment is made because the option holder at maturity receives only the underlying asset on that date and not the cash flow that has accrued to the asset during the life of the option. This cash flow is retained by the owner of the underlying asset.
We now want to use the Black-Scholes pricing model to price a European call option written on the S&P 500 index. On January 6, 2010, the value of the index was 1137.14. The European call option has a strike price of 1110 and 43 days to maturity. The risk-free interest rate for a 43-day holding period is found from the T-bill rates to be  per day (that is,
per day (that is,  ) and the dividend accruing to the index over the next 43 days is expected to be
) and the dividend accruing to the index over the next 43 days is expected to be  per day. For now, we assume the volatility of the index is
per day. For now, we assume the volatility of the index is  per day. Thus, we have
per day. Thus, we have

4.1. Model Implementation
The simple BSM model implies that a European option price can be written as a nonlinear function of six variables,
The stock price is readily available, and a treasury bill rate with maturity  can be used as the risk-free interest rate. The strike price and time to maturity are known features of any given option contract, thus only one parameter needs to be estimated—namely, the volatility, σ. As the option pricing formula is nonlinear, volatility can be estimated from a sample of n options on the same underlying asset, minimizing the mean-squared dollar pricing error (MSE):
can be used as the risk-free interest rate. The strike price and time to maturity are known features of any given option contract, thus only one parameter needs to be estimated—namely, the volatility, σ. As the option pricing formula is nonlinear, volatility can be estimated from a sample of n options on the same underlying asset, minimizing the mean-squared dollar pricing error (MSE):
Using prices on a sample of 103 call options traded on the S&P 500 index on January 6, 2010, we estimate the volatility, which minimizes the MSE to be  per day. This was the volatility estimate used in the numerical pricing example. Further details of this calculation can be found on the web page.
per day. This was the volatility estimate used in the numerical pricing example. Further details of this calculation can be found on the web page.
4.2. Implied Volatility
From Chapter 1, we know that the assumption of daily asset returns following the normal distribution is grossly violated in the data. We therefore should worry that an option pricing theory based on the normal distribution will not offer an appropriate description of reality. To assess the quality of the normality-based model, consider the so-called implied volatility calculated as
Returning to the preceding numerical example of the S&P 500 call option traded on January 6, 2010, knowing that the actual market price for the option was  , we can calculate the implied volatility to be
, we can calculate the implied volatility to be
If the normality assumption imposed on the model were true, then the implied volatility should be roughly constant across strike prices and maturities. However, actual option data displays systematic patterns in implied volatility, thus violating the normality-based option pricing theory. Figure 10.2 shows the implied volatility of various S&P 500 index call options plotted as a function of moneyness (S/X) on January 6, 2010. The picture shows clear evidence of the so-called smirk. Furthermore, the smirk is most evident at shorter horizons. As we will see shortly, this smirk can arise from skewness in the underlying distribution, which is ignored in the BSM model relying on normality. Options on foreign exchange tend to show a more symmetric pattern of implied volatility, which is referred to as the smile. The smile can arise from kurtosis in the underlying distribution, which is again ignored in the BSM model.
 |
| Figure 10.2 |
Smirk and smile patterns in implied volatility constitute evidence of misspecification in the BSM model. Consider for example pricing options with the BSM formula using a daily volatility of approximately 1% for all options. In Figure 10.2, the implied volatility is approximately 1% for at-the-money options for which  . Therefore, the BSM price would be roughly correct for these options. However, for options that are in-the-money—that is,
. Therefore, the BSM price would be roughly correct for these options. However, for options that are in-the-money—that is,  —the BSM implied volatility is higher than 1%, which says that the BSM model needs a higher than 1% volatility to fit the market data. This is because option prices are increasing in the underlying volatility. Using the BSM formula with a volatility of 1% would result in a BSM price that is too low. The BSM is thus said to underprice in-the-money call options. From the put-call parity formula, we can conclude that the BSM model also underprices out-of-the-money put options.
—the BSM implied volatility is higher than 1%, which says that the BSM model needs a higher than 1% volatility to fit the market data. This is because option prices are increasing in the underlying volatility. Using the BSM formula with a volatility of 1% would result in a BSM price that is too low. The BSM is thus said to underprice in-the-money call options. From the put-call parity formula, we can conclude that the BSM model also underprices out-of-the-money put options.
5. Allowing for Skewness and Kurtosis
We now introduce a relatively simple model that is capable of making up for some of the obvious mispricing in the BSM model. We again have one day returns defined as
Assuming that returns are independent over time, the skewness at horizon  can be written as a simple function of the daily skewness,
can be written as a simple function of the daily skewness,
We now define the standardized return at the  -day horizon as
-day horizon as

The Gram-Charlier density function  is an expansion around the normal density function,
is an expansion around the normal density function,  , allowing for a nonzero skewness,
, allowing for a nonzero skewness,  , and kurtosis
, and kurtosis  The Gram-Charlier expansion can approximate a wide range of densities with nonzero higher moments, and it collapses to the standard normal density when skewness and kurtosis are both zero. We notice the similarities with the Cornish-Fisher expansion for Value-at-Risk in Chapter 6, which is a similar expansion, but for the inverse cumulative density function instead of the density function itself.
The Gram-Charlier expansion can approximate a wide range of densities with nonzero higher moments, and it collapses to the standard normal density when skewness and kurtosis are both zero. We notice the similarities with the Cornish-Fisher expansion for Value-at-Risk in Chapter 6, which is a similar expansion, but for the inverse cumulative density function instead of the density function itself.

In this case, the call option price can be derived as being approximately equal to

5.1. Model Implementation
This GC model has three unknown parameters:  and
and  They can be estimated as before using a numerical optimizer minimizing the mean squared error
They can be estimated as before using a numerical optimizer minimizing the mean squared error
Notice this is just volatility times an additional term, which equals one if there is no skewness or kurtosis. Figure 10.3 plots two implied volatility curves for options with 10 days to maturity. One has a skewness of −3 and a kurtosis of 7 and shows the smirk, and the other has no skewness but a kurtosis of 8 and shows a smile.
 |
| Figure 10.3 |
The main advantages of the GC option pricing framework are that it allows for deviations from normality, that it provides closed-form solutions for option prices, and, most important, it is able to capture the systematic patterns in implied volatility found in observed option data. For example, allowing for negative skewness implies that the GC option price will be higher than the BSM price for in-the-money calls, thus removing the tendency for BSM to underprice in-the-money calls, which we saw in Figure 10.2.
6. Allowing for Dynamic Volatility
While the GC model is capable of capturing implied volatility smiles and smirks at a given point in time, it assumes that volatility is constant over time and is thus inconsistent with the empirical observations we made earlier. Put differently, the GC model is able to capture the strike price structure but not the maturity structure in observed options prices. In Chapter 4 and Chapter 5 we saw that variance varies over time in a predictable fashion: High-variance days tend to be followed by high-variance days and vice versa, which we modeled using GARCH and other types of models. When returns are independent, the standard deviation of returns at the  -day horizon is simply
-day horizon is simply  times the daily volatility, whereas the GARCH model implies that the term structure of variance depends on the variance today and does not follow the simple square root rule.
times the daily volatility, whereas the GARCH model implies that the term structure of variance depends on the variance today and does not follow the simple square root rule.
We now consider option pricing allowing for the underlying asset returns to follow a GARCH process. The GARCH option pricing model assumes that the expected return on the underlying asset is equal to the risk-free rate, rf, plus a premium for volatility risk, λ, as well as a normalization term. The observed daily return is then equal to the expected return plus a noise term. The noise term is conditionally normally distributed with mean zero and variance following a GARCH(1,1) process with leverage as in Chapter 4. By letting the past return feed into variance in a magnitude depending on the sign of the return, the leverage effect creates an asymmetry in the distribution of returns. This asymmetry is important for capturing the skewness implied in observed option prices.
Specifically, we can write the return process as

Notice that the expected value and variance of tomorrow's return conditional on all the information available at time t are

For a generic normally distributed variable  , we have that
, we have that  and therefore we get
and therefore we get

We can again solve for the option price using the risk-neutral expectation as in
Under risk neutrality, we must have that



An advantage of the GARCH option pricing approach introduced here is its flexibility: The previous analysis could easily be redone for any of the GARCH variance models introduced in Chapter 4. More important, it is able to fit observed option prices quite well.
6.1. Model Implementation
While we have found a way to price the European option under risk neutrality, unfortunately, we do not have a closed-form solution available. Instead, we have to use simulation to calculate the price
Now, for a given conditional variance  , and parameters
, and parameters  , we can use Monte Carlo simulation as in Chapter 8 to create future hypothetical paths of the asset returns. Parameter estimation will be discussed subsequently. Graphically, we can illustrate the simulation of hypothetical daily returns from day
, we can use Monte Carlo simulation as in Chapter 8 to create future hypothetical paths of the asset returns. Parameter estimation will be discussed subsequently. Graphically, we can illustrate the simulation of hypothetical daily returns from day  to the maturity on day
to the maturity on day  as
as


Once we have simulated, say, 5000 paths  each day until the maturity date
each day until the maturity date  , we can calculate the hypothetical risk-neutral asset prices at maturity as
, we can calculate the hypothetical risk-neutral asset prices at maturity as

Thus, we are using simulation to calculate the average future payoff, which is then used as an estimate of the expected value,  As the number of Monte Carlo replications gets infinitely large, the average will converge to the expectation. In practice, around 5000 replications suffice to get a reasonably precise estimate. The web site accompanying this book contains a spreadsheet with a Monte Carlo simulation calculating GARCH option prices.
As the number of Monte Carlo replications gets infinitely large, the average will converge to the expectation. In practice, around 5000 replications suffice to get a reasonably precise estimate. The web site accompanying this book contains a spreadsheet with a Monte Carlo simulation calculating GARCH option prices.
In theory, we could, of course, estimate all the parameters in the GARCH model using the maximum likelihood method from Chapter 4 on the underlying asset returns. But to obtain a better fit of the option prices, we can instead minimize the option pricing errors directly. Treating the initial variance  as a parameter to be estimated, we can estimate the GARCH option pricing model on a daily sample of options by numerically minimizing the mean squared error
as a parameter to be estimated, we can estimate the GARCH option pricing model on a daily sample of options by numerically minimizing the mean squared error
6.2. A Closed-Form GARCH Option Pricing Model
A significant drawback of the GARCH option pricing framework outlined here is clearly that it does not provide us with a closed-form solution for the option price, which must instead be calculated through simulation. Although the simulation technique is straightforward, it does take computing time and introduces an additional source of error arising from the approximation of the simulated average to the expected value.
Fortunately, if we are willing to accept a particular type of GARCH process, then a closed-form pricing formula exists. We will refer to this as the closed-form GARCH or CFG model. Assume that returns are generated by the process
The risk-neutral version of this process is

To verify that the risky assets earn the risk-free rate under the risk-neutral measure, we check again that

Under this special GARCH process for returns, the European option price can be calculated as
7. Implied Volatility Function (IVF) Models
The option pricing methods surveyed so far in this chapter can be derived from well-defined assumptions about the underlying dynamics of the economy. The next approach to European option pricing we consider is instead completely static and ad hoc but it turns out to offer reasonably good fit to observed option prices, and we therefore give a brief discussion of it here. The idea behind the approach is that the implied volatility smile changes only slowly over time. If we can therefore estimate a functional form on the smile today, then that functional form may work reasonably in pricing options in the near future as well.
The implied volatility smiles and smirks mentioned earlier suggest that option prices may be well captured by the following four-step approach:
1. Calculate the implied BSM volatilities for all the observed option prices on a given day as
2. Regress the implied volatilities on a second-order polynomial in moneyness and maturity. That is, use ordinary least squares (OLS) to estimate the a parameters in the regression
3. Compute the fitted values of implied volatility from the regression
4. Calculate model option prices using the fitted volatilities and the BSM option pricing formula, as in
Notice that this option pricing approach requires only a sequence of simple calculations and it is thus easily implemented.
While this four-step linear estimation approach is standard, we can typically obtain much better model option prices if the following modified estimation approach is taken. We can use a numerical optimization technique to solve for  by minimizing the mean squared error
by minimizing the mean squared error
8. Summary
This chapter has surveyed some key models for pricing European options. First, we introduced the simple but powerful binomial tree approach to option pricing. Then we discussed the famous Black-Scholes-Merton (BSM) model. The key assumption underlying the BSM model is that the underlying asset return dynamics are captured by the normal distribution with constant volatility. While the BSM model provides crucial insight into the pricing of derivative securities, the underlying assumptions are clearly violated by observed asset returns. We therefore next considered a generalization of the BSM model that was derived from the Gram-Charlier (GC) expansion around the normal distribution. The GC distribution allows for skewness and kurtosis and it therefore offers a more accurate description of observed returns than does the normal distribution. However, the GC model still assumes that volatility is constant over time, which we argued in earlier chapters was unrealistic. Next, we therefore presented two types of GARCH option pricing models. The first type allowed for a wide range of variance specifications, but the option price had to be calculated using Monte Carlo simulation or another numerical technique since no closed-form formula existed. The second type relied on a particular GARCH specification but in return provided a closed-form solution for the option price. Finally, we introduced the ad hoc implied volatility function (IVF) approach, which in essence consists of a second-order polynomial approximation of the implied volatility smile.
Appendix. The CFG Option Pricing Formula
The probabilities P1 and P2 in the closed-form GARCH (CFG) formula are derived by first solving for the conditional moment generating function. The conditional, time-t, moment generating function of the log asset prices as time  is
is

These functions can be solved by solving backward one period at a time from the maturity date using the terminal conditions
A fundamental result in probability theory establishes the following relationship between the characteristic function  and the probability density function
and the probability density function  :
:
Using these results, we can calculate the conditional expected payoff as


Further Resources
This chapter has focused on option pricing in discrete time in order to remain consistent with the previous chapters. There are many excellent textbooks on options. The binomial tree model in this chapter follows Hull (2011) who also provides a proof that the binomial model converges to the BSM model when the number of steps in the tree goes to infinity.
The classic papers on the BSM model are Black and Scholes (1973) and Merton (1973). The discrete time derivations in this chapter were introduced in Rubenstein (1976) and Brennan (1979). Merton (1976) introduced a continuous time diffusion model with jumps allowing for kurtosis in the distribution of returns. See Andersen and Andreasen (2000) for extensions to Merton's 1976 model.
For recent surveys on empirical option valuation, see Bates (2003), Garcia et al. (2010) and Christoffersen et al. (2010a).
The GC model is derived in Backus et al. (1997). The general GARCH option pricing framework is introduced in Duan (1995). Duan and Simonato (1998) discuss Monte Carlo simulation techniques for the GARCH model and Duan et al. (1999) contains an analytical approximation to the GARCH model price. Ritchken and Trevor (1999) suggest a trinomial tree method for calculating the GARCH option price.
Duan (1999) and Christoffersen et al. (2010b) consider extensions to the GARCH option pricing model allowing for conditionally nonnormal returns. The closed-form GARCH option pricing model is derived in Heston and Nandi (2000) and extended in Christoffersen et al. (2006).
Christoffersen and Jacobs (2004a) compared the empirical performance of various GARCH variance specifications for option pricing and found that the simple variance specification including a leverage effect as applied in this chapter works very well compared with the BSM model.
Hsieh and Ritchken (2005) compared the GARCH (GH) and the closed-form GARCH (CFG) models and found that the GH model performs the best in terms of out-of-sample option valuation. See Christoffersen et al. (2008) and Christoffersen et al. (2010a) for option valuation using the GARCH component models described in Chapter 4.
GARCH option valuation models with jumps in the innovations have been developed by Christoffersen et al. (2011) and Ornthanalai (2011).
Hull and White (1987) and Heston (1993) derived continuous time option pricing models with time-varying volatility. Bakshi et al. (1997) contains an empirical comparison of Heston's model with more general models and finds that allowing for time-varying volatility is key in fitting observed option prices. Lewis (2000) discusses the implementation of option valuation models with time-varying volatility.
The IVF model is described in Dumas et al. (1998) and the modified IVF model (MIVF) is examined in Christoffersen and Jacobs (2004b), who find that the MIVF model performs very well empirically compared with the simple BSM model. Berkowitz (2010) provides a theoretical justification for the MIVF approach. Bams et al. (2009) discuss the choice of objective function in option model calibration.
Andersen, L.; Andreasen, J., Jump-diffusion processes: Volatility smile fitting and numerical methods for option pricing, Rev. Derivatives Res. 4 (2000) 231–262.
Backus, D.; Foresi, S.; Li, K.; Wu, L., Accounting for Biases in Black-Scholes. (1997) The Stern School at New York University; Manuscript.
Bakshi, G.; Cao, C.; Chen, Z., Empirical performance of alternative option pricing models, J. Finance 52 (1997) 2003–2050.
Bams, D.; Lehnert, T.; Wolff, C., Loss functions in option valuation: A framework for selection, Manag. Sci. 55 (2009) 853–862.
Bates, D., Empirical option pricing: A retrospection, J. Econom. 116 (2003) 387–404.
Berkowitz, J., On justifications for the ad hoc Black-Scholes method of option pricing, Stud. Nonlinear Dyn. Econom. 14 (1) (2010); Article 4.
Black, F.; Scholes, M., The pricing of options and corporate liabilities, J. Polit. Econ. 81 (1973) 637–659.
Brennan, M., The pricing of contingent claims in discrete time models, J. Finance 34 (1979) 53–68.
Christoffersen, P.; Dorion, C.; Jacobs, K.; Wang, Y., Volatility components: Affine restrictions and non-normal innovations, J. Bus. Econ. Stat. 28 (2010) 483–502.
Christoffersen, P.; Elkamhi, R.; Feunou, B.; Jacobs, K., Option valuation with conditional heteroskedasticity and non-normality, Rev. Financ. Stud. 23 (2010) 2139–2183.
Christoffersen, P.; Heston, S.; Jacobs, K., Option valuation with conditional skewness, J. Econom. 131 (2006) 253–284.
Christoffersen, P.; Jacobs, K., Which GARCH model for option valuation?Manag. Sci. 50 (2004) 1204–1221.
Christoffersen, P.; Jacobs, K., The importance of the loss function in option valuation, J. Financ. Econ. 72 (2004) 291–318.
Christoffersen, P.; Jacobs, K.; Ornthanalai, C., GARCH option valuation, theory and evidence, In: (Editors: Duan, J.-C.; Gentle, J.; Hardle, W.) Handbook of Computational Finance (2010) Springer, New York, NY; forthcoming.
Christoffersen, P.; Jacobs, K.; Ornthanalai, C., Exploring time-varying jump intensities: Evidence from S&P 500 returns and options, Available from: SSRN,http://ssrn.com/abstract=1101733 (2011).
Christoffersen, P.; Jacobs, K.; Ornthanalai, C.; Wang, Y., Option valuation with long-run and short-run volatility components, J. Financ. Econ. 90 (2008) 272–297.
Duan, J., The GARCH option pricing model, Math. Finance 5 (1995) 13–32.
Duan, J., Conditionally Fat-Tailed Distributions and the Volatility Smile in Options. (1999) Hong Kong University of Science and Technology; Manuscript.
Duan, J.; Gauthier, G.; Simonato, J.-G., An analytical approximation for the GARCH option pricing model, J. Comput. Finance 2 (1999) 75–116.
Duan, J.; Simonato, J.-G., Empirical martingale simulation for asset prices, Manag. Sci. 44 (1998) 1218–1233.
Dumas, B.; Fleming, J.; Whaley, R., Implied volatility functions: Empirical tests, J. Finance 53 (1998) 2059–2106.
Garcia, R.; Ghysels, E.; Renault, E., The econometrics of option pricing, In: (Editors: Aït-Sahalia, Y.; Hansen, L.P.) Handbook of Financial Econometrics (2010) Elsevier, North Holland, pp. 479–552.
Heston, S., A closed-form solution for options with stochastic volatility, with applications to bond and currency options, Rev. Financ. Stud. 6 (1993) 327–343.
Heston, S.; Nandi, S., A closed-form GARCH option pricing model, Rev. Financ. Stud. 13 (2000) 585–626.
Hsieh, K.; Ritchken, P., An empirical comparison of GARCH option pricing models, Rev. Derivatives Res. 8 (2005) 129–150.
Hull, J., Options, Futures and Other Derivatives. eighth ed (2011) Prentice-Hall, Upper Saddle River, NJ.
Hull, J.; White, A., The pricing of options on assets with stochastic volatilities, J. Finance 42 (1987) 281–300.
Lewis, A., Option Valuation under Stochastic Volatility. (2000) Finance Press, Newport Beach, California.
Merton, R., Theory of rational option pricing, Bell J. Econ. Manag. Sci. 4 (1973) 141–183.
Merton, R., Option pricing when underlying stock returns are discontinuous, J. Financ. Econ. 3 (1976) 125–144.
Ornthanalai, C., A new class of asset pricing models with Levy processes: Theory and applications, Available from: SSRN,http://ssrn.com/abstract=1267432 (2011).
Ritchken, P.; Trevor, R., Pricing options under generalized GARCH and stochastic volatility processes, J. Finance 54 (1999) 377–402.
Rubenstein, M., The valuation of uncertain income streams and the pricing of options, Bell J. Econ. Manag. Sci. 7 (1976) 407–425.
Open the Chapter10Data.xlsx file from the web site. The file contains European call options on the S&P 500 from January 6, 2010.
1. Calculate the BSM price for each option using a standard deviation of 0.01 per day. Using Solver, find the volatility that minimizes the mean squared pricing error using 0.01 as a starting value. Keep the BSM prices that correspond to this optimal volatility and use these prices below.
2. Scatter plot the BSM pricing errors (actual price less model price) against moneyness defined as (S/X) for the different maturities.
4. Fit the Gram-Charlier option price to the data. Estimate a model with skewness only. Use nonlinear test squares (NLS).
5. Regress implied volatility on a constant, moneyness, the time-to-maturity divided by 365, each variable squared, and their cross product. Calculate the fitted BSM volatility from the regression for each option. Calculate the ad hoc IVF price for each option using the fitted values for volatility.
6. Redo the IVF estimation using NLS to minimize the mean squared pricing error (MSE). Call this MIVF. Use the IVF regression coefficients as starting values.
7. Calculate the square root of the mean squared pricing error from the IVF and MIVF models and compare them to the square root of the MSE from the standard BSM model and the Gram-Charlier model. Scatter plot the pricing errors from the MIVF model against moneyness and compare them to the plots from exercise 2.
The answers to these exercises can be found in the Chapter10Results.xlsx file on the companion site.
For more information see the companion site at http://www.elsevierdirect.com/companions/9780123744487
..................Content has been hidden....................
You can't read the all page of ebook, please click here login for view all page.

