Chapter 8
Staying Ahead of the Curves: Polynomials
IN THIS CHAPTER
![]() Examining the standard polynomial form
Examining the standard polynomial form
![]() Graphing and finding polynomial intercepts
Graphing and finding polynomial intercepts
![]() Determining function signs on intervals
Determining function signs on intervals
![]() Using the tools of algebra to dig up rational roots
Using the tools of algebra to dig up rational roots
![]() Taking on synthetic division in a natural fiber world
Taking on synthetic division in a natural fiber world
The word polynomial comes from poly-, meaning many, and -nomial, meaning name or designation. Binomial (two terms) and trinomial (three terms) are two of the many names or designations used for selected polynomials. The terms in a polynomial are made up of numbers and letters that get stuck together with multiplication.
Although the name may seem to imply complexity (much like Albert Einstein, Pablo Picasso, or Mary Jane Sterling), polynomials are some of the easier functions or equations to work with in algebra. The exponents used in polynomials are all whole numbers — no fractions or negatives. Polynomials get progressively more interesting as the exponents get larger — they can have more intercepts and turning points. This chapter outlines what you can do with polynomials: factor them, graph them, analyze them to pieces — everything but make a casserole with them. The graph of a polynomial looks like a Wisconsin landscape — smooth, rolling curves. Are you ready for this ride?
Taking a Look at the Standard Polynomial Form
A polynomial function is a specific type of function that can be easily spotted in a crowd of other types of functions and equations. The exponents on the variable terms in a polynomial function are always whole numbers. And, by convention, you write the terms from the largest exponent to the smallest. Actually, the exponent 0 on the variable makes the variable factor equal to 1, so you don’t see a variable there at all — just a constant, if there is one.
A traditional standard equation for the terms of a polynomial function is shown here. Don’t let all the subscripts and superscripts throw you. The letter a is repeated with numbers, rather than giving the terms coefficients a, b, c, and so on, because a polynomial with a degree higher than 26 would run out of letters in the English alphabet.
The general form for a polynomial function is
Here, the a’s are real numbers and the n’s are whole numbers. The last term is technically ![]() , if you want to show the variable in every term.
, if you want to show the variable in every term.
Exploring Polynomial Intercepts and Turning Points
The intercepts of a polynomial are the points where the graph of the curve of the polynomial crosses the x- and y-axes. A polynomial function has exactly one y-intercept, but it can have any number of x-intercepts, depending on the degree of the polynomial (the powers of the variable). The higher the degree, the more x-intercepts you might have.
The x-intercepts of a polynomial are also called the roots, zeros, or solutions. You may think that mathematicians can’t make up their minds about what to call these values, but they do have their reasons; depending on the application, the x-intercept has an appropriate name for what you’re working on (see Chapter 3 for more information on this algebra name game). The nice thing is that you use the same technique to solve for the intercepts, no matter what they’re called. (Lest the y-intercept feel left out, it’s frequently called the initial value.)
The x-intercepts are often where the graph of the polynomial goes from positive values (above the x-axis) to negative values (below the x-axis) or from negative values to positive values. Sometimes, though, the values on the graph don’t change sign at an x-intercept: These graphs take on a touch and go appearance. The graphs approach the x-axis, seem to change their minds about crossing the axis, touch down at the intercepts, and then go back to the same side of the axis.
A turning point of a polynomial is where the graph of the curve changes direction. It can change from going upward to going downward, or vice versa. A turning point is where you find a relative maximum value of the polynomial, an absolute maximum value, a relative minimum value, or an absolute minimum value.
Interpreting relative value and absolute value
As I introduce in Chapter 5, many functions can have an absolute maximum or an absolute minimum value — the point at which the graph of the function has no higher or lower value, respectively. For example, a parabola opening downward has an absolute maximum — you see no point on the curve that’s higher than the maximum. In other words, no value of the function is greater than that number. (Check out Chapter 6 for more on quadratic functions and their parabola graphs.) Some functions, however, also have relative maximum or minimum values:
- Relative maximum: A point on the graph — a value of the function — that’s relatively large; the point is higher than anything around it, but you may be able to find a higher point somewhere else on the graph.
- Relative minimum: A point on the graph — a value of the function — that’s lower than anything close to it; it’s lower relative to all the points on the curve near it.
In Figure 8-1, you can see five turning points. Two are relative maximum values, which means they’re higher than any points close to them. Three are minimum values, which means they’re lower than any points around them. Two of the minimums are relative minimum values, and one is absolutely the lowest point on the curve. This function has no absolute maximum value because it keeps going up and up without end.

John Wiley & Sons, Inc.
FIGURE 8-1: Extreme points on a polynomial.
Counting intercepts and turning points
The number of potential turning points and x-intercepts of a polynomial function is good to know when you’re sketching the graph of the function. You can count the number of x-intercepts and turning points of a polynomial if you have the graph of it in front of you, but you can also make an estimate of the number if you have the equation of the polynomial. Your estimate is actually a number that represents the most points that can occur. You can say, “There are at most n intercepts and at most m turning points.” The estimate is the best you can do, but that’s usually not a bad thing.
To determine the rules for the greatest number of possible intercepts and greatest number of possible turning points from the equation of a polynomial, you look at the general form of a polynomial function.
Examine the following two function equations as examples of polynomials. To determine the possible number of intercepts and turning points for the functions, look for the values of n, the exponents that have the highest values:
This graph has at most seven x-intercepts (7 is the highest power in the function) and six turning points ![]() .
.
This graph has at most six x-intercepts and five turning points.
You can see the graphs of these two functions in Figure 8-2. According to its function, the graph of the first example (Figure 8-2a) could have at least seven x-intercepts, but it has only five; it does have all six turning points, though. You can also see that two of the intercepts are touch-and-go types, meaning that they approach the x-axis before heading away again. The graph of the second example (Figure 8-2b) can have at most six x-intercepts, but it has only two; it does have all five turning points.

John Wiley & Sons, Inc.
FIGURE 8-2: The intercept and turning point behavior of two polynomial functions.
Figure 8-3 provides you with two extreme polynomial examples. The graphs of ![]() (Figure 8-3a) and
(Figure 8-3a) and ![]() (Figure 8-3b) seem to have great possibilities … that don’t pan out. The graph of
(Figure 8-3b) seem to have great possibilities … that don’t pan out. The graph of ![]() , according to the rules of polynomials, could have as many as eight intercepts and seven turning points. But, as you can see from the graph, it has no intercepts and just one turning point. The graph of
, according to the rules of polynomials, could have as many as eight intercepts and seven turning points. But, as you can see from the graph, it has no intercepts and just one turning point. The graph of ![]() has only one intercept and no turning points.
has only one intercept and no turning points.

John Wiley & Sons, Inc.
FIGURE 8-3: A polynomial’s highest power provides information on the most-possible turning points and intercepts.
Solving for polynomial intercepts
You can easily solve for the y-intercept of a polynomial function, of which you can find only one. The y-intercept is where the curve of the graph crosses the y-axis, and that’s when ![]() . So, to determine the y-intercept for any polynomial, simply replace all the x’s with zeros and solve for y (that’s the y part of the coordinate of that intercept):
. So, to determine the y-intercept for any polynomial, simply replace all the x’s with zeros and solve for y (that’s the y part of the coordinate of that intercept):
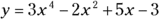
- When
 ,
, 
- The y-intercept is
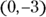 .
. 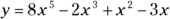
- When
 ,
, 
- The y-intercept is (0, 0), at the origin.
After you complete the easy task of solving for the y-intercept, you find out that the x-intercepts are another matter altogether. The value of y is zero for all x-intercepts, so you let ![]() and solve for x.
and solve for x.
Here, however, you don’t have the advantage of making everything disappear except the constant number like you do when solving for the y-intercept. When solving for the x-intercepts, you may have to factor the polynomial or perform a more elaborate process — techniques you can find later in this chapter in the section “Factoring for polynomial roots” or “Saving your sanity: The Rational Root Theorem,” respectively. For now, just apply the process of factoring and setting the factored form equal to zero to some carefully selected examples. This is essentially using the multiplication property of zero — setting the factored form equal to zero to find the intercepts (see Chapter 1).
To determine the x-intercepts of the following three polynomials, replace the y’s with zeros and solve for the x’s:

- When
 ,
,  ,
,  ,
,  (using the square root rule from Chapter 3)
(using the square root rule from Chapter 3) 
- When
 ,
,  ,
,  (using the multiplication property of zero from Chapter 1)
(using the multiplication property of zero from Chapter 1) 
- When
 ,
,  ,
,  or
or  (using the multiplication property of zero)
(using the multiplication property of zero)
Both of these intercepts come from multiple roots (when a solution appears more than once). Another way of writing the factored form is
You could list the answer as ![]() . The number of times a root repeats is significant when you’re graphing. A multiple root has a different kind of look or graph where it intersects the axis. (For more, head to the section “Changing from roots to factors” later in this chapter.)
. The number of times a root repeats is significant when you’re graphing. A multiple root has a different kind of look or graph where it intersects the axis. (For more, head to the section “Changing from roots to factors” later in this chapter.)
Determining Positive and Negative Intervals
When a polynomial has positive y-values for some interval — between two x-values — its graph lies above the x-axis. When a polynomial has negative values, its graph lies below the x-axis in that interval. The only way to change from positive to negative values or vice versa is to go through zero — in the case of a polynomial, at an x-intercept. Polynomials can’t jump from one side of the x-axis to the other because their domains are all real numbers — nothing is skipped to allow such a jump. The fact that x-intercepts work this way is good news for you because x-intercepts play a large role in the big picture of solving polynomial equations and determining the positive and negative natures of polynomials.
The positive versus negative values of polynomials are important in various applications in the real world, especially where money is involved. If you use a polynomial function to model the profit in your business or the depth of water (above or below flood stage) near your house, you should be interested in positive versus negative values and in what intervals they occur. The technique you use to find the positive and negative intervals also plays a big role in calculus, so you get an added bonus by using it here first.
Using a sign-line
If you’re a visual person like me, you’ll appreciate the interval method I present in this section. Using a sign-line and marking the intervals between x-values allows you to determine where a polynomial is positive or negative, and it appeals to your artistic bent!
The function ![]() , for example, changes sign at every intercept. Setting
, for example, changes sign at every intercept. Setting ![]() and solving, you find that the x-intercepts are at
and solving, you find that the x-intercepts are at ![]() . Now you can put this information about the problem to work.
. Now you can put this information about the problem to work.
To determine the positive and negative intervals for a polynomial function, follow this method:
- Draw a number line, and place the values of the x-intercepts in their correct positions on the line.

Choose random values to the right and left of the intercepts to test whether the function is positive or negative in those positions.
If the function equation is factored, you determine whether each factor is positive or negative, and you find the sign of the product of all the factors.
Some possible random number choices are
 , and 8. These values represent numbers in each interval determined by the intercepts. (Note: These aren’t the only possibilities; you can pick your favorites.)
, and 8. These values represent numbers in each interval determined by the intercepts. (Note: These aren’t the only possibilities; you can pick your favorites.) . You don’t need the actual number value, just the sign of the result, so
. You don’t need the actual number value, just the sign of the result, so  .
. , so
, so  .
. , so
, so  .
. , so
, so  .
. , so
, so  .
.You need to check only one point in each interval; the function values all have the same sign within that interval.
- Place a
 or
or  symbol in each interval to show the function sign.
symbol in each interval to show the function sign.

The graph of this function is positive, or above the x-axis, whenever x is smaller than
 , between 0 and 2, and bigger than 7. You write that
, between 0 and 2, and bigger than 7. You write that  when:
when:  or
or  or
or  . In interval notation, that’s
. In interval notation, that’s  .
.
The function ![]() doesn’t change at each intercept. The intercepts are where
doesn’t change at each intercept. The intercepts are where ![]() .
.
- Draw the number line and insert the intercepts.

Test values to the left and right of each intercept. Some possible random choices are to let
 .
.When you can, you should always use 0, because it combines so nicely.
 is
is  .
. is
is 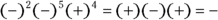 .
. is
is  .
. is
is  .
.- Mark the signs in the appropriate places on the number line.

You probably noticed that the factors raised to an even power were always positive. The factor raised to an odd power is only positive when the result in the parentheses is positive.
Interpreting the rule
Look back at the two polynomial examples in the previous section. Did you notice that in the first example, the sign changed every time, and in the second, the signs were sort of stuck on the same sign for a while? When the signs of functions don’t change, the graphs of the polynomials don’t cross the x-axis at any intercepts, and you see touch-and-go graphs. Why do you suppose this is? First, look at graphs of two functions from the previous section in Figures 8-4a and 8-4b, ![]() and
and ![]() .
.

John Wiley & Sons, Inc.
FIGURE 8-4: Comparing graphs of polynomials that have differing sign behaviors.
The rule for whether a function displays sign changes or not at the intercepts is based on the exponent on the factor that provides you with a particular intercept.
So, for example, with the function ![]() , shown in Figure 8-5a, you see a sign change at
, shown in Figure 8-5a, you see a sign change at ![]() and no sign change at
and no sign change at ![]() . With the function
. With the function ![]() , shown in Figure 8-5b, you never see a sign change.
, shown in Figure 8-5b, you never see a sign change.

John Wiley & Sons, Inc.
FIGURE 8-5: The powers of a polynomial determine whether the curve crosses the x-axis.
Finding the Roots of a Polynomial
Finding intercepts (or roots or zeros) of polynomials can be relatively easy or a little challenging, depending on the complexity of the function. Factored polynomials have roots that just stand up and shout at you, “Here I am!” Polynomials that factor easily are very desirable. Polynomials that don’t factor at all, however, are relegated to computers or graphing calculators.
The polynomials that remain are those that factor — with a little planning and work. The planning process involves counting the number of possible positive and negative real roots and making a list of potential rational roots. The work is using synthetic division to test the list of choices to find the roots.
Factoring for polynomial roots
Finding x-intercepts of polynomials isn’t difficult — as long as you have the polynomial in nicely factored form. You just set the y equal to zero and use the multiplication property of zero (see Chapter 1) to pick the intercepts off like flies. But what if the polynomial isn’t in factored form (and it should be)? What do you do? Well, you factor it, of course. This section deals with easily recognizable factors of polynomials — types that probably account for 70 percent of any polynomials you’ll have to deal with. (I cover other, more challenging types in the following sections.)
Applying factoring patterns and groupings
Half the battle is recognizing the patterns in factorable polynomial functions. You want to take advantage of the patterns. If you don’t see any patterns (or if none exist), you need to investigate further. The most easily recognizable factoring patterns used on polynomials are the following (which I brush up on in Chapter 1):
Difference of squares
Greatest common factor
Difference of cubes
Sum of cubes
Perfect square trinomial
UnFOIL
Trinomial factorization
Grouping
Common factors in groups
The following examples incorporate the different methods of factoring. They contain perfect cubes and squares and all sorts of good combinations of factorization patterns.
To factor the following polynomial, for example, you should use the greatest common factor and then the difference of squares:

This polynomial requires factoring, using the sum of two perfect cubes:

You initially factor the next polynomial by grouping. The first two terms have a common factor of ![]() , and the second two terms have a common factor of
, and the second two terms have a common factor of ![]() . The terms in the new equation have a common factor of
. The terms in the new equation have a common factor of ![]() . After performing the factorization, you see that the first factor is the difference of squares and the second is the difference of cubes:
. After performing the factorization, you see that the first factor is the difference of squares and the second is the difference of cubes:

This last polynomial shows how you first use the greatest common factor and then factor with a perfect square trinomial:
Considering the unfactorable
Life would be wonderful if you would always find your paper on the doorstep in the morning and if all polynomials would factor easily. I won’t get into the trials and tribulations of newspaper delivery, but polynomials that can’t be factored do need to be discussed. You can’t just give up and walk away. In some cases, polynomials can’t be factored, but they do have intercepts that are decimal values that go on forever. Other polynomials both can’t be factored and have no x-intercepts.
If a polynomial doesn’t factor, you can attribute the roadblock to one of two things:
- The polynomial doesn’t have x-intercepts. You can tell that from its graph using a graphing calculator. This situation happens with some even-degreed polynomials.
- The polynomial has irrational roots or zeros. These can be estimated with a graphing calculator or computer. All odd-powered polynomials have at least one x-intercept.
Irrational roots means that the x-intercepts are written with radicals or rounded-off decimals. Irrational numbers are those that you can’t write as fractions; you usually find them as square roots of numbers that aren’t perfect squares or cube roots of numbers that aren’t perfect cubes. You can sometimes solve for irrational roots if one of the factors of the polynomial is a quadratic. You can apply the quadratic formula to find that solution (see Chapter 3).
For instance, polynomials in these forms don’t factor:
 where
where  . A polynomial in this form has no real roots or solutions. Refer to Chapter 14 on how to deal with imaginary numbers.
. A polynomial in this form has no real roots or solutions. Refer to Chapter 14 on how to deal with imaginary numbers. . The quadratic formula will help you determine the imaginary roots.
. The quadratic formula will help you determine the imaginary roots. . This form requires the quadratic formula, too. You’ll get imaginary roots.
. This form requires the quadratic formula, too. You’ll get imaginary roots.
The second and third examples above are part of the factorization of the difference or sum of two cubes. In Chapter 3, you see how the difference or sum of cubes are factored, and you’re told, there, that the resulting trinomial doesn’t factor.
Saving your sanity: The Rational Root Theorem
What do you do if the factorization of a polynomial doesn’t leap out at you? You have a feeling that the polynomial factors, but the necessary numbers escape you. Never fear! Your faithful author has just saved your day. My help is in the form of the Rational Root Theorem. This theorem is really neat because it’s so orderly and predictable, and it has an obvious end to it; you know when you’re done so you can stop looking for solutions. But before you can put the theorem into play, you have to be able to recognize a rational root — or a rational number, for that matter.
What distinguishes rational numbers from their opposites, irrational numbers, has to do with the decimal equivalences. The decimal associated with a fraction (rational number) will either terminate or repeat (have a pattern of numbers that occurs over and over again). The decimal equivalent of an irrational number never repeats and never ends; it just wanders on aimlessly.
Without further ado, here’s the Rational Root Theorem: If the polynomial ![]() has any rational roots, they all meet the requirement that you can write them as a fraction equal to
has any rational roots, they all meet the requirement that you can write them as a fraction equal to ![]() .
.
In other words, according to the theorem, any rational root of a polynomial is formed by dividing a factor of the constant term by a factor of the lead coefficient.
Putting the theorem to good use
The Rational Root Theorem gets most of its workout by letting you make a list of numbers that may be roots of a particular polynomial. After using the theorem to make your list of potential roots (and check it twice), you plug the numbers into the polynomial to determine which, if any, work. You may run across an instance where none of the candidates work, which tells you that there are no rational roots. (And if a given rational number isn’t on the list of possibilities that you come up with, it can’t be a root of that polynomial.)
Before you start to plug and chug, however, check out the section “Letting Descartes make a ruling on signs,” later in this chapter. It helps you with your guesses. Also, you can refer to “Synthesizing Root Findings” for a quicker method than plugging in.
POLYNOMIALS WITH CONSTANT TERMS
To find the roots of the polynomial ![]() , for example, you test the following possibilities:
, for example, you test the following possibilities: ![]() and
and ![]() . These values are all the factors of the number 12. Technically, you divide each of these factors of 12 by the factors of the lead coefficient, but because the lead coefficient is 1 (as in
. These values are all the factors of the number 12. Technically, you divide each of these factors of 12 by the factors of the lead coefficient, but because the lead coefficient is 1 (as in ![]() ), dividing by that number won’t change a thing. Note: You ignore the signs, because the factors for both 12 and 1 can be positive or negative, and you find several combinations that can give you a positive or negative root. You find out the sign when you test the root in the function equation.
), dividing by that number won’t change a thing. Note: You ignore the signs, because the factors for both 12 and 1 can be positive or negative, and you find several combinations that can give you a positive or negative root. You find out the sign when you test the root in the function equation.
To find the roots of another polynomial, ![]() , you first list all the factors of 20:
, you first list all the factors of 20: ![]() and
and ![]() . Now divide each of those factors by the factors of 6. You don’t need to bother dividing by 1, but you need to divide each by 2, 3, and 6:
. Now divide each of those factors by the factors of 6. You don’t need to bother dividing by 1, but you need to divide each by 2, 3, and 6:

You may have noticed some repeats in the previous list that occur when you reduce fractions. For instance, ![]() is the same as
is the same as ![]() , and
, and ![]() is the same as
is the same as ![]() . Even though this looks like a mighty long list, between the integers and fractions, it still gives you a reasonable number of candidates to try out. You can check them off in a systematic manner.
. Even though this looks like a mighty long list, between the integers and fractions, it still gives you a reasonable number of candidates to try out. You can check them off in a systematic manner.
POLYNOMIALS WITHOUT CONSTANT TERMS
When a polynomial doesn’t have a constant term, you first have to factor out the greatest power of the variable that you can. If you’re looking for the possible rational roots of ![]() , for example, and you want to use the Rational Root Theorem, you get nothing but zeros. You have no constant term — or you can say the constant is zero, so all the numerators of the fractions would be zero.
, for example, and you want to use the Rational Root Theorem, you get nothing but zeros. You have no constant term — or you can say the constant is zero, so all the numerators of the fractions would be zero.
You can overcome the problem by factoring out the factor of ![]()
![]() . The factored out x gives you the root zero. Now you apply the Rational Root Theorem to the new polynomial in the parentheses to get the possible roots:
. The factored out x gives you the root zero. Now you apply the Rational Root Theorem to the new polynomial in the parentheses to get the possible roots:
Changing from roots to factors
When you have the factored form of a polynomial and set it equal to 0, you can solve for the solutions (or x-intercepts, if that’s what you want). Just as important, if you have the solutions, you can go backward and write the factored form. Factored forms are needed when you have polynomials in the numerator and denominator of fractions and you want to reduce the fraction. Factored forms are easier to compare with one another.
How can you use the Rational Root Theorem to factor a polynomial function? Why would you want to? The answer to the second question, first, is that you can reduce a factored form if it’s in a fraction. Also, a factored form is more easily graphed. Now, for the first question: You use the Rational Root Theorem to find roots of a polynomial and then translate those roots into binomial factors whose product is the polynomial. (For methods on how to actually find the roots from the list of possibilities that the Rational Root Theorem gives you, see the sections “Letting Descartes make a ruling on signs” and “Using synthetic division to test for roots.”)
To find the factors of a polynomial with the five roots ![]() ,
, ![]() ,
, ![]() ,
, ![]() , and
, and ![]() , for example, you apply the previously stated rule to get
, for example, you apply the previously stated rule to get ![]() . The k indicates that a constant multiplier may exist, so many polynomials actually have the same roots. To get rid of the fractions, you multiply the polynomial by 4 to get
. The k indicates that a constant multiplier may exist, so many polynomials actually have the same roots. To get rid of the fractions, you multiply the polynomial by 4 to get ![]()
![]() . Notice that the positive roots give factors of the form
. Notice that the positive roots give factors of the form ![]() , and the negative roots give factors of the form
, and the negative roots give factors of the form ![]() , which comes from
, which comes from ![]() .
.
To show multiple roots, or roots that occur more than once, use exponents on the factors. For instance, if the roots of a polynomial are ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , and
, and ![]() , the corresponding polynomial is
, the corresponding polynomial is ![]() .
.
Letting Descartes make a ruling on signs
Rene Descartes was a French philosopher and mathematician. One of his contributions to algebra is Descartes’ Rule of Signs. This handy, dandy rule is a weapon in your arsenal for the fight to find roots of polynomial functions. If you pair this rule with the Rational Root Theorem from the previous section, you’ll be well equipped to succeed.
The Rule of Signs tells you how many positive and negative real roots you may find in a polynomial. A real number is just about any number you can think of. It can be positive or negative, rational or irrational. The only thing it can’t be is imaginary. (I cover imaginary numbers in Chapter 14 if you want to know more about them.)
Counting up the positive roots
The first part of the Rule of Signs helps you identify how many of the real roots of a polynomial are positive.
To use Part 1 of Descartes’ Rule of Signs on the polynomial ![]()
![]() , for example, you count the number of sign changes. The sign of the first term is positive, the second is a negative, and the third is positive; then negative, positive, stays positive, negative, and then positive. Whew! In total, you count six sign changes. Therefore, you conclude that the polynomial has six positive roots, four positive roots, two positive roots, or none at all. Out of seven roots possible, it looks like at least one has to be negative. (By the way, this polynomial does have six positive roots; I built it that way! The only way you’d know that without being told is to go ahead and find the roots, with help from the Rule of Signs.)
, for example, you count the number of sign changes. The sign of the first term is positive, the second is a negative, and the third is positive; then negative, positive, stays positive, negative, and then positive. Whew! In total, you count six sign changes. Therefore, you conclude that the polynomial has six positive roots, four positive roots, two positive roots, or none at all. Out of seven roots possible, it looks like at least one has to be negative. (By the way, this polynomial does have six positive roots; I built it that way! The only way you’d know that without being told is to go ahead and find the roots, with help from the Rule of Signs.)
Changing the function to count negative roots
Along with the positive roots (see the previous section), Descartes’ Rule of Signs deals with the possible number of negative roots of a polynomial. After you count the possible number of positive real roots, you combine that value to the number of possible negative real roots to make your guesses and solve the equation.
To determine the possible number of negative roots of the polynomial ![]() , for example, you first find
, for example, you first find ![]() by replacing each x with
by replacing each x with ![]() and simplifying:
and simplifying:
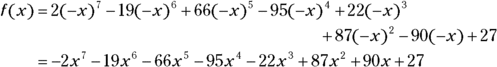
As you can see, the function has only one sign change, from negative to positive. Therefore, the function has exactly one negative root — no more, no less.
Synthesizing Root Findings
You use synthetic division to test the list of possible roots for a polynomial that you come up with by using the Rational Root Theorem (see the section “Saving your sanity: The Rational Root Theorem” earlier in the chapter). Synthetic division is a method of dividing a polynomial by a binomial, using only the coefficients of the terms in the polynomial and the constant in the binomial. The method is quick, neat, and highly accurate — usually even more accurate than long division — and it uses most of the information from earlier sections in this chapter, putting it all together for the search for roots/zeros/intercepts of polynomials. (You can find more information about, and practice problems for, long division and synthetic division in one of my other spine-tingling thrillers, Algebra I Workbook For Dummies.)
You can interpret your results in three different ways, depending on what purpose you’re using synthetic division for. I explain each way in the following sections.
Using synthetic division to test for roots
When you want to use synthetic division to test for roots in a polynomial, the last number on the bottom row of your synthetic division problem is the telling result. If that number is zero, the division had no remainder, and the number being tested is a root. The fact that there’s no remainder means that the binomial represented by the number is dividing the polynomial evenly. The number is a root because the binomial is a factor.
The polynomial ![]() , for example, has zeros or roots when
, for example, has zeros or roots when ![]() . You could find as many as five real roots, which you can tell from the exponent 5 on the first x. Using Descartes’ Rule of Signs (see the previous section), you find two or zero positive real roots (indicated by the two sign changes). Replacing each x with
. You could find as many as five real roots, which you can tell from the exponent 5 on the first x. Using Descartes’ Rule of Signs (see the previous section), you find two or zero positive real roots (indicated by the two sign changes). Replacing each x with ![]() , the polynomial now reads
, the polynomial now reads ![]() . Again, using the Rule of Signs, you find three or one negative real roots. (Counting up the number of positive and negative roots helps when you’re making a guess as to what a root may be.)
. Again, using the Rule of Signs, you find three or one negative real roots. (Counting up the number of positive and negative roots helps when you’re making a guess as to what a root may be.)
Now, using the Rational Root Theorem (see the section “Saving your sanity: The Rational Root Theorem”), your list of the potential rational roots is ![]() . You choose one of these and apply synthetic division.
. You choose one of these and apply synthetic division.
Keeping in mind that smaller is better in this case, the following process shows a guess that ![]() is a root.
is a root.
The steps for performing synthetic division on a polynomial to find its roots are as follows:
Write the polynomial in order of decreasing powers of the exponents. Replace any missing powers with zero to represent the coefficient.
In this case, you’ve lucked out. The polynomial is already in the correct order:
 .
.- Write the coefficients in a row, including any zeros.

Put the number you want to divide by in front of the row of coefficients, separated by a half-box.
In this case, the guess is
 .
.
- Draw a horizontal line below the row of coefficients, leaving room for numbers under the coefficients.

- Bring the first coefficient straight down below the line.

- Multiply the number you bring below the line by the number that you’re dividing into everything. Put the result under the second coefficient.

- Add the second coefficient and the product, putting the result below the line.

- Repeat the multiplication/addition from Steps 6 and 7 with the rest of the coefficients.

The last entry on the bottom is a zero, so you know ![]() is a root. Now, you can do a modified synthetic division when testing for the next root; you just use the numbers across the bottom except the bottom right zero entry. (These values are actually coefficients of the quotient, if you do long division; see the following section.)
is a root. Now, you can do a modified synthetic division when testing for the next root; you just use the numbers across the bottom except the bottom right zero entry. (These values are actually coefficients of the quotient, if you do long division; see the following section.)
If your next guess is to see if ![]() is a root, the modified synthetic division appears as follows:
is a root, the modified synthetic division appears as follows:

The last entry on the bottom row isn’t zero, so ![]() isn’t a root.
isn’t a root.
The really good guessers amongst you decide to try ![]() ,
, ![]() ,
, ![]() , and
, and ![]() (a second time). These values represent the rest of the roots, and the synthetic division for all the guesses looks like this:
(a second time). These values represent the rest of the roots, and the synthetic division for all the guesses looks like this:
First, trying the ![]() ,
,

The last number in the bottom row is 0. That’s the remainder in the division. So now just look at all the numbers that come before the 0; they’re the new coefficients to divide into. Notice that the last coefficient is now 16, so you can modify your list of possible roots to be just the factors of 16. Also, they’re all positive with no sign changes. You don’t have any positive roots left. Now, dividing by ![]() :
:

In the next division, you consider only the negative factors of 4:
This time, dividing by ![]() ,
,

The last number in the row is 0, so ![]() is a root. Repeat the division, and you find that
is a root. Repeat the division, and you find that ![]() is a double root:
is a double root:

Your job is finished when you see the number one remaining in the last row, before the zero.
Now you can collect all the numbers that divided evenly — the roots of the equation — and use them to write the answer to the equation that’s set equal to zero or to write the factorization of the polynomial or to sketch the graph with these numbers as x-intercepts. In this case, the roots are ![]() and
and ![]() . The factorization (see the section “Changing from roots to factors” earlier in this chapter) is
. The factorization (see the section “Changing from roots to factors” earlier in this chapter) is ![]() .
.
Synthetically dividing by a binomial
Finding the roots of a polynomial isn’t the only excuse you need to use synthetic division. You can also use synthetic division to replace the long, drawn-out process of dividing a polynomial by a binomial. Divisions like this are found in lots of calculus problems — where you need to make the expression more simplified so you can perform some wonderful operation.
The polynomial being divided can be any degree; the binomial has to be either ![]() or
or ![]() , and the coefficient on the x is 1. This may seem rather restrictive, but a huge number of long divisions you’d have to perform fit in this category, so it helps to have a quick, efficient method to perform these basic division problems.
, and the coefficient on the x is 1. This may seem rather restrictive, but a huge number of long divisions you’d have to perform fit in this category, so it helps to have a quick, efficient method to perform these basic division problems.
To use synthetic division to divide a polynomial by a binomial, you first write the polynomial in decreasing order of exponents, inserting a zero for any missing exponent. The number you put in front or divide by is the opposite of the number in the binomial. So, if you divide ![]() by the binomial
by the binomial ![]() , you use
, you use ![]() in the synthetic division, as shown here:
in the synthetic division, as shown here:
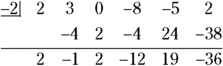
As you can see, the last entry on the bottom row isn’t zero. If you’re looking for roots of a polynomial equation, this fact tells you that ![]() isn’t a root. In this case, because you’re working on a long division application (which you know because you need to divide to simplify the expression), the
isn’t a root. In this case, because you’re working on a long division application (which you know because you need to divide to simplify the expression), the ![]() is the remainder of the division — in other words, the division doesn’t come out even.
is the remainder of the division — in other words, the division doesn’t come out even.
You obtain the answer (quotient) of the division problem from the coefficients across the bottom of the synthetic division. You start with a power one value lower than the original polynomial’s power, and you use all the coefficients, dropping the power by one with each successive coefficient. The last coefficient is the remainder, which you write over the divisor.
Here’s the division problem and its solution. The original division problem is written first. After the problem, you see the coefficients from the synthetic division written in front of variables — starting with one degree lower than the original problem. The remainder of ![]() is written in a fraction on top of the divisor,
is written in a fraction on top of the divisor, ![]() .
.

Wringing out the Remainder (Theorem)
In the two previous sections, you use synthetic division to test for roots of a polynomial equation and then to do a long division problem. You use the same synthetic division process, but you read and use the results differently. In this section, I present yet another use of synthetic division involving the Remainder Theorem. When you’re looking for roots or solutions of a polynomial equation, you always want the remainder from the synthetic division to be zero. In this section, you get to see how to make use of all those pesky remainders that weren’t zeros.
For instance, in the division problem from the previous section, ![]()
![]() has a remainder of
has a remainder of ![]() . Therefore, according to the Remainder Theorem, for the function
. Therefore, according to the Remainder Theorem, for the function ![]() ,
, ![]() .
.
The Remainder Theorem comes in very handy when finding function values because you’ll find it much easier to do synthetic division, where you multiply and add repeatedly, than to have to substitute numbers in for variables, raise the numbers to high powers, multiply by the coefficients, and then combine the terms.
Using the Remainder Theorem to find f (3) when ![]()
![]() , for example, you apply synthetic division to the coefficients using 3 as the divider in the half-box.
, for example, you apply synthetic division to the coefficients using 3 as the divider in the half-box.

The remainder of the division by ![]() is 83, and, by the Remainder Theorem,
is 83, and, by the Remainder Theorem, ![]() . Compare the process you use here with substituting the 3 into the function:
. Compare the process you use here with substituting the 3 into the function: ![]() . These numbers get really large. For instance,
. These numbers get really large. For instance, ![]() . The numbers are much more manageable when you use synthetic division and the Remainder Theorem.
. The numbers are much more manageable when you use synthetic division and the Remainder Theorem.

 Given the polynomial
Given the polynomial  If n is an odd number, you know right away that you have to find at least one x-intercept. If n is even, you may not find any x-intercepts.
If n is an odd number, you know right away that you have to find at least one x-intercept. If n is even, you may not find any x-intercepts. The moral to the story of
The moral to the story of