Chapter 17
Everything You Wanted to Know about Sets
IN THIS CHAPTER
![]() Conquering set notation
Conquering set notation
![]() Performing algebraic operations on sets
Performing algebraic operations on sets
![]() Circling the wagons with Venn diagrams
Circling the wagons with Venn diagrams
![]() Addressing factorials in sets
Addressing factorials in sets
![]() Using permutations and combinations to count set elements
Using permutations and combinations to count set elements
![]() Making set life easy with tree diagrams and the binomial theorem
Making set life easy with tree diagrams and the binomial theorem
Back in the 1970s, a book titled Everything You Always Wanted to Know About Sex — But Were Afraid to Ask (Bantam) hit the shelves of stores everywhere. The book caused quite a buzz. Nowadays, however, people don’t seem to be afraid to ask about — or inform you about — anything. So, in the modern spirit, this chapter lets it all hang out. Here you find out all the deep, dirty secrets concerning sets. I cover the union and intersection of sets, complementary sets, counting on sets, and drawing some very revealing pictures. Can you handle it?
Revealing Set Notation
A set is a collection of items. The items may be people, pairs of shoes, or numbers, for example, but they usually have something in common — even if the only characteristic that ties them together is the fact that they appear in the same set. The items in a set are called the set’s elements.
Mathematicians have developed some specific notation and rules to help you maneuver through the world of sets. The symbols and vocabulary aren’t difficult to master; you just have to remember what they mean. Familiarizing yourself with set notation is like learning a new language.
Listing elements with a roster
The name of a set appears as a capital letter (A in the following example, for instance) to distinguish it from other sets. To introduce the elements of a set, you put them in roster notation, which just means to list the elements. For example, if a set A contains the first five whole numbers, you write the set as follows:
You list the elements in the set inside the braces and separate them by commas. The order in which you list the elements doesn’t matter. You could also say that ![]() , for example.
, for example.
Building sets from scratch
A simple way to describe a set (other than set notation; see the previous section) is to use rule or set builder notation. For example, you can write the set ![]() as follows:
as follows:
You read the set builder notation as “A is the set containing all x such that x is an element of W, the whole numbers, and x is less than 5.” The vertical bar, ![]() , separates the variable from its rule, and the epsilon,
, separates the variable from its rule, and the epsilon, ![]() , means “is an element of.” This is all wonderful math shorthand.
, means “is an element of.” This is all wonderful math shorthand.
You may be wondering why in the world anyone would want to use this longwinded notation when listing the elements is easy enough. You’d be right to wonder; it doesn’t make sense in the previous example, but what if you want to talk about a set B that contains all the odd numbers between 0 and 100? Do you really want to list all the elements?
Going for all (universal set) or nothing (empty set)
Consider the sets ![]() and
and ![]() . Set F contains three elements, and set I contains four elements. Within these sets, you can branch out to a set that you call the universal set for F and I. You can also distinguish a set called the empty set, or null set. This all or nothing business lays the foundation for performing set operations (see the section “Operating on Sets” later in this chapter).
. Set F contains three elements, and set I contains four elements. Within these sets, you can branch out to a set that you call the universal set for F and I. You can also distinguish a set called the empty set, or null set. This all or nothing business lays the foundation for performing set operations (see the section “Operating on Sets” later in this chapter).
The following list presents the characteristics of these all or nothing sets:
Universal set: A universal set for one or more sets contains all the possible elements in a particular category. The writer of the situation must decide how many elements need to be considered in a particular problem. But one characteristic is pretty standard: The universal set is denoted U.
For example, you could say that the universal set for
 and
and 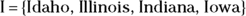 is
is  . But the universal set for F and I doesn’t have to be a set containing all the states; it can just be all the states that start with a vowel.
. But the universal set for F and I doesn’t have to be a set containing all the states; it can just be all the states that start with a vowel.Empty (or null) set: The opposite of the universal set is the empty set (or null set). The empty set doesn’t contain anything (no kidding!). The two types of notation used to indicate the empty set are
 and
and  . The first notation resembles a zero with a slash through it, and the second is empty braces. You must use one notation or the other, not both at the same time, to indicate that you have the empty set.
. The first notation resembles a zero with a slash through it, and the second is empty braces. You must use one notation or the other, not both at the same time, to indicate that you have the empty set.For example, if you want to list all the elements in set G, where G is the set that contains all the states starting with the letter Q, you write
 . You have the empty set because no states in the United States start with the letter Q.
. You have the empty set because no states in the United States start with the letter Q.
Subbing in with subsets
The real world provides many special titles for the little guy. Apartments can have sublets, movies can have subtitles, and ships can be submarines, so of course sets can have subsets. A subset is a set completely contained within another set — no element in a subset is absent from the set it’s a subset of. Whew! That’s a mouthful, and my sentence ends with a preposition. For the sake of good English, I’ll start calling the sets subsets and supersets — a superset representing what the subset is a subset of (there I go again!).
Indicating subsets with notation
The set ![]() is a subset of
is a subset of ![]() . Set B is a subset of set C, because B is completely contained in C. Set C consists of all the numbers that are powers of 2, where the powers are all elements of the set of integers (Z). The notation for “subset of” is
. Set B is a subset of set C, because B is completely contained in C. Set C consists of all the numbers that are powers of 2, where the powers are all elements of the set of integers (Z). The notation for “subset of” is ![]() , and you write
, and you write ![]() to say that B is a subset of C.
to say that B is a subset of C.
Another way you can write the superset ![]() is
is ![]()
![]() , using ellipses to indicate that the set continues on forever.
, using ellipses to indicate that the set continues on forever.
Counting the number of subdivisions
Have a look at the following listings of some selected sets and all their subsets. Notice that I include the empty set in each list of subsets. I do so because the empty set fulfills the definition that no element of the subset is absent from the superset. Here’s the first set:
The subsets of
are
.
The set A has four subsets: two subsets with one element, one with no elements, and one with both elements from the original set.
Here’s a pet-themed set:
The subsets of
are {dog}, {cat}, {mouse}, {dog, cat}, {dog, mouse}, {cat, mouse},
, {dog, cat, mouse}.
The set B has eight subsets: three subsets with one element, three with two elements, one with no elements, and one with all the elements from the original set.
Time to get a bit bigger:
The subsets of set
are {r}, {s}, {t}, {u}, {r, s}, {r, t}, {r, u}, {s, t}, {s, u}, {t, u}, {r, s, t}, {r, s, u}, {r, t, u}, {s, t, u},
, {r, s, t, u}.
The set C has 16 subsets: four subsets with one element, six with two elements, four with three elements, one with no elements, and one with all the elements.
Have you determined a pattern yet? See if the following information helps:
- A set with two elements has four subsets.
- A set with three elements has eight subsets.
- A set with four elements has sixteen subsets.
The number of subsets produced by a set is equal to a power of 2.
You can apply this rule to the set ![]() , for example. The set has six elements, so it has
, for example. The set has six elements, so it has ![]() subsets. Knowing the number of subsets a set has doesn’t necessarily help you list them all, but it lets you know if you’ve missed any. (Check out the section “Mixing up sets with combinations” to find out how many subsets of each type [number of elements] a set has.)
subsets. Knowing the number of subsets a set has doesn’t necessarily help you list them all, but it lets you know if you’ve missed any. (Check out the section “Mixing up sets with combinations” to find out how many subsets of each type [number of elements] a set has.)
Operating on Sets
Algebra provides three basic operations that you can perform on sets: union, intersection, and complement (negation). The operations union and intersection take two sets at a time to perform them — much like addition and subtraction take two numbers. Finding the complement of a set (or negating it) is like finding the opposite of the set, so you perform it on only one set at a time.
Celebrating the union of two sets
Finding the union of two sets is like merging two companies. You put them together to make one big set (forming unions probably isn’t as lucrative, however).
- Set

- Set


You can also say that each set is a subset of the union of the sets.
You can apply the union operation on more than two sets at a time (but you have to have at least two sets). For instance, if you have sets ![]() ,
, ![]() , and
, and ![]() , the union
, the union ![]() . Again, you mention each element only once in the union of the sets.
. Again, you mention each element only once in the union of the sets.
A couple of special unions involve subsets and the empty set. What happens when you perform the union of two sets, and one set is the subset of the other? For instance, say you have ![]() and
and ![]() . You can write the union as
. You can write the union as ![]() , because the union of the sets is just the set G. H is a subset of G — every element in H is contained in G. Also, because H is a subset of G, H must also be a subset of the union of the two sets,
, because the union of the sets is just the set G. H is a subset of G — every element in H is contained in G. Also, because H is a subset of G, H must also be a subset of the union of the two sets, ![]() .
.
Because the empty set is a subset of every set, you can say ![]() ,
, ![]() ,
, ![]() , and so on. Think of how adding zero to a number affects the number — it doesn’t.
, and so on. Think of how adding zero to a number affects the number — it doesn’t.
Looking both ways for set intersections
The intersection of two sets is like the intersection of two streets. If Main Street runs east and west and University Street runs north and south, they share the street where they intersect. The street department doesn’t have to pave the intersection twice, because the two streets share that little part.
- Set

- Set


If set A is a subset of another set, the intersection of A and its superset is just the set A. For instance, if set ![]() and
and ![]() ,
, ![]() .
.
The intersection of any set with the empty set is just the empty set.
Feeling complementary about sets
The complement of set A, written ![]() (or sometimes
(or sometimes ![]() ), contains every element that doesn’t appear in A. Every item that doesn’t appear in a set can be plenty of things — unless you limit your search.
), contains every element that doesn’t appear in A. Every item that doesn’t appear in a set can be plenty of things — unless you limit your search.
Counting the elements in sets
Situations often arise when you need to be able to tell how many elements a set contains. When sets appear in probability, logic, or other mathematical problems, you don’t always care what the elements are — just how many of them sit in the sets. The notation indicating that you want to know the number of elements contained in a set is ![]() , meaning “The number of elements in set A is k.” The number k will always be some whole number: 0, 1, 2, and so on. The number of elements in a set is sometimes referred to the set’s cardinal number.
, meaning “The number of elements in set A is k.” The number k will always be some whole number: 0, 1, 2, and so on. The number of elements in a set is sometimes referred to the set’s cardinal number.
Consider the sets ![]() and
and ![]() , for example. The union of A and B,
, for example. The union of A and B, ![]() , equals {2, 3, 4, 6, 8, 9, 10, 12, 14, 15, 16, 18, 20, 21}, and the intersection,
, equals {2, 3, 4, 6, 8, 9, 10, 12, 14, 15, 16, 18, 20, 21}, and the intersection, ![]() , equals {6, 12, 18}. You can apply the previous formula to count the number of elements in each set and the results of the operations. Here are the different bits of input:
, equals {6, 12, 18}. You can apply the previous formula to count the number of elements in each set and the results of the operations. Here are the different bits of input: ![]() ,
, ![]() ,
, ![]() , and
, and ![]() .
.
Filling the numbers into the rule, you find ![]() . This is a true statement. Checking your arithmetic to be sure that you’ve figured the problem correctly is useful.
. This is a true statement. Checking your arithmetic to be sure that you’ve figured the problem correctly is useful.
Drawing Venn You Feel Like It
Venn diagrams are pictures that show the relationships between two or more sets and the elements in those sets. The adage “a picture is worth a thousand words” is never truer than with these diagrams. Venn diagrams can help you sort out a situation and come to a conclusion. Many problems that you solve by using Venn diagrams come in paragraphs — plenty of words and numbers and confusing relationships. Labeling the circles in the diagrams and filling in numbers helps you determine how everything works together — and allows you to see if you’ve forgotten anything.
For instance, the Venn diagram in Figure 17-1 shows set A, which contains the letters of the alphabet that spell encyclopedia, and set B, which contains the letters in the alphabet that rhyme with “see.” Both sets are encased in the universal set — all the letters in the alphabet.

John Wiley & Sons, Inc.
FIGURE 17-1: A Venn diagram with two sets enclosed by the universal set.
Notice that the letters c, d, e, and p appear in both sets. The Venn diagram makes it easy to see where the elements are and what characteristics they have — which elements are shared and which are special to each set.
Applying the Venn diagram
The business of sorting letters based on their placement in a word or what they rhyme with, which you see in examples in the previous section, may not seem very fulfilling. The actual applications get a little more complicated, but the examples here show you the basics. Some actual uses of Venn diagrams appear in the world of advertising (charting types of advertising and the results), of politics (figuring out who has what opinions on issues and how to make use of their votes), of genetics and medicine (looking at characteristics and reactions based on symptoms and results), and so on. The following example shows, in a simplified version, how useful Venn diagrams can be.
A Chicago-area newspaper interviewed 40 people to determine if they were Chicago White Sox fans and/or if they cheered for the Chicago Bears. (For those of you who couldn’t care less about sports, the White Sox are a baseball team, and the Bears are a football team.) Of the people interviewed, 25 are White Sox fans, 9 like both the Sox and the Bears, and 7 don’t care for either team. How many people are Bears fans?
As you can see, 25 White Sox ![]() 9 who like both
9 who like both ![]() 7 who don’t care for
7 who don’t care for ![]() , which is more than the 40 people interviewed. The process has to have some overlap. You can sort out the overlap with a Venn diagram. You create one circle for White Sox fans, another for Bears fans, and a rectangle for all the people interviewed. Start by putting the seven fans who don’t cheer for either team outside the circles (but inside the rectangle). You then put the 9 who like both teams in the intersection of the two circles (see Figure 17-2).
, which is more than the 40 people interviewed. The process has to have some overlap. You can sort out the overlap with a Venn diagram. You create one circle for White Sox fans, another for Bears fans, and a rectangle for all the people interviewed. Start by putting the seven fans who don’t cheer for either team outside the circles (but inside the rectangle). You then put the 9 who like both teams in the intersection of the two circles (see Figure 17-2).

John Wiley & Sons, Inc.
FIGURE 17-2: Watch for the overlap created by combining two groups.
The number of White Sox fans is 25, so, if you put 16 in only the Sox’s circle, the number in the entire circle (including the overlap) sums to 25. The only area missing is the circle where people are Bears fans but not Sox fans. So far, you have a total of ![]() people. Therefore, you can say that 8 people root for the Bears but not the Sox. You put an 8 in that area, and you see that the number of Bears fans totals 17 people (see Figure 17-3).
people. Therefore, you can say that 8 people root for the Bears but not the Sox. You put an 8 in that area, and you see that the number of Bears fans totals 17 people (see Figure 17-3).

John Wiley & Sons, Inc.
FIGURE 17-3: You find that 17 Chicagoans root for Da Bears.
Using Venn diagrams with set operations
You often get to use the set operations union, intersection, and complement (see the section “Operating on Sets”) in different combinations when doing algebra problems. In these situations, Venn diagrams are useful for sorting some of the more complex statements.
For instance, is it true that ![]() (translated as “the complement of the union of C and D equals the intersection of the complement of C and the complement of D”)? You can sketch each of these situations to compare them by using Venn diagrams. You use shading to signify parts of a particular statement.
(translated as “the complement of the union of C and D equals the intersection of the complement of C and the complement of D”)? You can sketch each of these situations to compare them by using Venn diagrams. You use shading to signify parts of a particular statement.
In Figure 17-4a, you see ![]() shaded in — every element that appears in both C and D. In Figure 17-4b, you see
shaded in — every element that appears in both C and D. In Figure 17-4b, you see ![]() shaded. The complement represents every element that is not in the specified set (but is in the universal set), so it’s like the negative of a photograph — all the opposite areas are shaded.
shaded. The complement represents every element that is not in the specified set (but is in the universal set), so it’s like the negative of a photograph — all the opposite areas are shaded.

John Wiley & Sons, Inc.
FIGURE 17-4: Identifying the union (a) and the complement of the union (b).
Now you can deal with the other half of the equation. First, in Figure 17-5a, you see ![]() shaded in. The shaded area represents every element that isn’t in C. In Figure 17-5b, you see both
shaded in. The shaded area represents every element that isn’t in C. In Figure 17-5b, you see both ![]() and
and ![]() shaded in, and their intersection (the elements they share) is much darker to show where they overlap. Does the overlap match the sketch for
shaded in, and their intersection (the elements they share) is much darker to show where they overlap. Does the overlap match the sketch for ![]() ? Yes, Figures 17-4b and 17-5b are the same — the same areas are shaded in, so you’ve confirmed the equation.
? Yes, Figures 17-4b and 17-5b are the same — the same areas are shaded in, so you’ve confirmed the equation.

John Wiley & Sons, Inc.
FIGURE 17-5: The darker shading represents  .
.
The Venn diagrams show that two completely different statements can be equal. Sets and set operations are hard to work with in terms of algebra, which is why using a picture approach, like Venn diagrams, goes a long way toward showing or proving that an equation or other statement is true. Using Venn diagrams to pick apart compound statements gives an accurate and visual verification.
Adding a set to a Venn diagram
Showing the relationship between the elements of two sets with a Venn diagram is pretty straightforward. But, as with most mathematical processes, you can take the diagram one step further and illustrate the relationship between three sets. You can also handle four sets, but the diagram gets pretty hairy and isn’t all that useful because of the way you have to draw the figure.
When two sets overlap, you divide the picture into four distinct areas: outside both circles, the overlap of the circles, and the two parts that have no overlap but appear in one circle or the other. When you overlap three circles in a Venn diagram, you create eight distinct areas. Figure 17-6 shows you how to complete the process.

John Wiley & Sons, Inc.
FIGURE 17-6: The eight district areas created by the intersection of three circles.
You can describe the eight different areas determined by the intersection of three circles as follows:
- All the elements in A only
- All the elements shared by A and B but not by C
- All the elements in B only
- All the elements shared by A and C but not by B
- All the elements shared by A, B, and C
- All the elements shared by B and C but not by A
- All the elements in C only
- All the elements not in A, B, or C
You may have to use a setup like this to sort out information and answer questions. For instance, say that a club with 25 members decides to order pizza for its next meeting; the secretary takes a poll to see what people like:
- 14 people like sausage.
- 10 people like pepperoni.
- 13 people like mushrooms.
- 5 people like both sausage and pepperoni.
- 10 people like both sausage and mushrooms.
- 7 people like both pepperoni and mushrooms.
- 4 people like all three toppings.
Here’s the big question: How many people don’t like any of the three toppings on their pizzas?
As you can see, the preferences sum to many more than 25, so you definitely have to account for some overlaps. You can answer the question by drawing three intersecting circles, labeling them Sausage, Pepperoni, and Mushrooms, and filling in numbers, starting with the last on the given list. Figure 17-7a shows the initial Venn diagram you can use.

John Wiley & Sons, Inc.
FIGURE 17-7: With a Venn diagram, you can tell how many people want a plain cheese pizza.
You put the 4, representing people who like all three toppings, in the middle section. Seven people like both pepperoni and mushrooms, but you already account for four of them in the middle, so put a 3 in the area for pepperoni and mushrooms, but not sausage. Ten people like both sausage and mushrooms, but you already put four of those people in the middle area, so put a 6 in the area for sausage and mushrooms, but not pepperoni. Five people like both sausage and pepperoni, but you already account for four; put a 1 in the sausage and pepperoni section, but not mushrooms. Figure 17-7b shows all these entries.
Now you can fill in the rest of the circles. Thirteen people like mushrooms, and you already have 13 people in that circle, so put 0 for people who like mushrooms only. Ten people like pepperoni; you already have 8 in that circle, so put a 2 for pepperoni only. Fourteen people like sausage, so put a 3 in the section for sausage only to account for the difference. Look at all those filled-in numbers in Figure 17-7c!
You finish by adding all the numbers in Figure 17-7c. The numbers add to 19 people. The club has 25 members, so you conclude that 6 of them must not like sausage, pepperoni, or mushrooms. You can order a plain cheese pizza for these picky folk.
Focusing on Factorials
When you perform a factorial operation, you multiply the number you’re operating on times every positive integer smaller than that number. The factorial operation is denoted by an exclamation mark, !. I cover the factorial operation in Chapter 16 and use it in some of the sequences in that chapter, but it doesn’t truly come into its own until you use it with permutations, combinations, and probability problems (as you can see in the “How Do I Love Thee? Let Me Count Up the Ways” section later in this chapter).
One of the main reasons you use the factorial operation in conjunction with sets is to count the number of elements in the sets. When the numbers are nice, discrete, small values, you have no problem. But when the sets get very large — such as the number of handshakes that occur when everyone in a club of 40 people shakes hands with everyone else — you want a way to do a systematic count. Factorials are built into the formulas that allow you to do such counting.
Making factorial manageable
When you apply the factorial operation to a counting problem or algebra expansion of binomials, you run the risk of producing a very large number. Just look at how fast the factorial grows:

Check out the last two numbers in the list. You see that 10! has the same digits as 9! — only with an extra zero. This observation illustrates one of the properties of the factorial operation. Another property is the definition of 0! (zero factorial).
The two properties (or rules) for the factorial operation are as follows:
 : To find n!, you multiply the number n times the factorial that comes immediately before it.
: To find n!, you multiply the number n times the factorial that comes immediately before it. : The value of zero factorial is one. You just have to trust this one.
: The value of zero factorial is one. You just have to trust this one.
If you know that ![]() , and you want 14!, you can try your calculator first. Most hand-held calculators go into scientific notation when you get to numbers this large. The calculator won’t give you the exact value — it rounds off to eight decimal places. But, if you’re industrious, you can find 14! with the first property from the previous list:
, and you want 14!, you can try your calculator first. Most hand-held calculators go into scientific notation when you get to numbers this large. The calculator won’t give you the exact value — it rounds off to eight decimal places. But, if you’re industrious, you can find 14! with the first property from the previous list: ![]() (multiplied by hand!).
(multiplied by hand!).
Simplifying factorials
The process of simplifying factorials in fractions, multiplication problems, or formulas is simple enough, as long as you keep in mind how the factorial operation works. For instance, if you want to simplify the fraction ![]() , you can’t just divide the 8 by the 4 to get 2!. The factorials just don’t work that way. You’ll find that reducing the fraction by using factorial properties is much easier and more accurate than trying to divide the huge numbers created by the factorials.
, you can’t just divide the 8 by the 4 to get 2!. The factorials just don’t work that way. You’ll find that reducing the fraction by using factorial properties is much easier and more accurate than trying to divide the huge numbers created by the factorials.
You have a string of numbers multiplied together, so the product of all those numbers lends itself to factorization or reduction of a fraction. Look at the two factorials written out:
You have two options to simplify this factorial:
- You can write out and cancel out all the factors of 4! and multiply what’s left:

- You can take advantage of the rule
 (see the previous section) when writing the larger factorial:
(see the previous section) when writing the larger factorial:
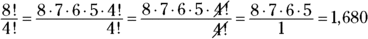
You see how useful this process is when you have to compute something with factorials such as ![]() . The value of 40! is huge, and so is the value of 37!. But the reduced form of the example fraction is quite nice. You can reduce the fraction by using the first property of factorials:
. The value of 40! is huge, and so is the value of 37!. But the reduced form of the example fraction is quite nice. You can reduce the fraction by using the first property of factorials:

The values 39 and 38 in the numerator are each divisible by one of the factors in the denominator. You multiply what you have left for your answer.
How Do I Love Thee? Let Me Count Up the Ways
You may think that you know everything there is to know about counting. After all, you’ve been counting since your parents asked you, a 3-year-old, how many toes you have and how many cookies are on the plate. Counting toes and cookies is a breeze. Counting very, very large sets of elements is where the challenge comes in. Fortunately, algebra provides you with some techniques for counting large sets of elements more efficiently: the multiplication principle, permutations, and combinations (for more in-depth info on these topics, check out Probability For Dummies [Wiley], by Deborah Rumsey, PhD). You use each counting technique in a decidedly different situation, although deciding which technique to use is often the biggest challenge.
Applying the multiplication principle to sets
For instance, if you have six shirts, four pairs of pants, eight pairs of socks, and two pairs of shoes, you have ![]() different ways to get dressed. Of course, this doesn’t take into account any color or style issues.
different ways to get dressed. Of course, this doesn’t take into account any color or style issues.
How many different license plates are available in a state with the following rules:
- All the plates have three letters followed by two numbers.
- The first letter can’t be O.
- The first number can’t be zero or one.
Think of this problem as a prime candidate for the multiplication principle. Here’s the first rule for the license plate:
You can’t use O for the first letter, so that leaves 25 ways to choose the first letter. The second and third letters have no restrictions, so you can choose any one of the 26 letters for them. The first number can’t be zero or one, so that leaves you eight choices. The second number has no restrictions, so you have all ten choices. You simply multiply these choices together to get your answer: ![]() . You can assume that this isn’t a very big state if it has only a million or so license-plate possibilities. And trust me, using the multiplication principle to find this answer is faster than going to the DMV for help!
. You can assume that this isn’t a very big state if it has only a million or so license-plate possibilities. And trust me, using the multiplication principle to find this answer is faster than going to the DMV for help!
Arranging permutations of sets
The permutation of some set of elements is the rearrangement of the order of those elements. For example, you can rearrange the letters in the word “act” to spell six different words (well, not actual words; they could possibly be acronyms for something): act, cat, atc, cta, tac, tca. Therefore, you say that for the word “act,” you have six permutations of three elements.
Counting the permutations
Knowing how many permutations a set of elements has doesn’t tell you what those permutations are, but you at least know how many permutations to look for. When you find the number of permutations for a set of elements, you select where you get the elements from and how many you need to rearrange. You assume that you don’t replace any of the elements you select before you choose again.
With that number, I hope you don’t plan on taking a picture of each arrangement!
Here’s an example that illustrates some broader observations of permutations. Say that the seven dwarfs want to line up for a family photo. How many different ways can the dwarfs line up for the picture? In algebraic terms, you want a permutation of seven things taken seven at a time. Using the previous formula, you find the following:
Now you can see why mathematicians had to declare that ![]() (which I explain in the “Making factorial manageable” section earlier in the chapter). In the formula, you end up with a 0! in the denominator, because the number of items chosen is the same as the number of items available. By saying that
(which I explain in the “Making factorial manageable” section earlier in the chapter). In the formula, you end up with a 0! in the denominator, because the number of items chosen is the same as the number of items available. By saying that ![]() , the denominator becomes a 1, and the answer becomes the value in the numerator of the fraction.
, the denominator becomes a 1, and the answer becomes the value in the numerator of the fraction.
When using the formula for permutations of n elements taken r at a time,
 . When you use all the elements in the arrangements, you just need to find n!.
. When you use all the elements in the arrangements, you just need to find n!. . When you take only one of the elements from all the choices, you have only n different arrangements.
. When you take only one of the elements from all the choices, you have only n different arrangements. . When you don’t use any of the elements from the set, you have only one way to do that.
. When you don’t use any of the elements from the set, you have only one way to do that.
Some problems call for a mixture of permutations and the multiplication principle (see the previous section). Say, for example, that you want to make up a new password for your computer account. The first rule for the system is that the first two entries must be letters — with no repeats, and you can’t use O or I. The next four entries must be digits — with no restrictions. You can then enter two more letters with no restrictions. Finally, the last three entries must be three digits with no repeats. How many different passwords are possible?
Break down the problem into its four different parts, setting up the multiplication principle to combine the four parts:
You can now set up the permutations:
- The arrangement of the first two letters is a permutation of 24 elements taken 2 at a time.
- The next four digits give you 10 choices each time — multiplied together.
- The following two letters give you 26 choices each time — multiplied together.
- The final three digits represent a permutation of 10 elements taken 3 at a time.
The computation goes as follows:

You calculate over two-and-a-half trillion different passwords. Hopefully, the rules will keep the hackers out. Now you just have to remember your password!
Distinguishing one permutation from another
If you’re lining up the books on your bookshelf based on color — for eye appeal — rather than subject or author, you aren’t distinguishing between the different red books and the different blue books. And if you want to know the total number of permutations of the letters in the word “cheese,” you can’t distinguish between “cheese” and “cheese,” where you switch the e’s around. You can’t tell the permutations apart, so you don’t count rearrangements of the same letter as different permutations. The way you counter this effect is to use the formula for distinguishable permutations.
Using this formula, you can determine the number of distinguishable permutations of the word “cheese” (see the section “Focusing on Factorials” for the division part of this formula):
Cheese has six letters altogether, and the three e’s are all the same.
You can also apply the formula to the books on the bookshelf. Say that you have ten blue books, five red books, six black books, one green book, and one gray book. You have over ![]() possible distinguishable arrangements of the books. You can determine this number by using the formula for distinguishable permutations. You have 23 books total and can make 23! arrangements of all the books at once:
possible distinguishable arrangements of the books. You can determine this number by using the formula for distinguishable permutations. You have 23 books total and can make 23! arrangements of all the books at once:
Now say you want to put all the books of the same color together, and you don’t care about the order of the books in each color grouping. How many different arrangements are possible? This problem is a permutation of the five colors (blue, red, black, green, and gray). A permutation of 5 elements taken 5 at a time is ![]() different arrangements (see the section “Focusing on Factorials” for more on this calculation).
different arrangements (see the section “Focusing on Factorials” for more on this calculation).
Being the finicky decorator that you are, you now decide that the arrangements within each color matter, and you want the books arranged in groups of the same color. How many different arrangements are possible? This problem involves the permutations of the different colors first and then permutations of the books in the blue, red, and black groups. Doing the math, you find the following:

You have quite a few ways to arrange the books on the bookshelf. Maybe alphabetical order makes more sense.
Mixing up sets with combinations
Combination is a precise mathematical term that refers to how you can choose a certain number of elements from a set. Unlike permutations, with combinations the order in which the elements appear doesn’t matter. Combinations, for example, allow you to determine how many different ways you can choose three people to serve on a committee (the order in which you choose them doesn’t matter — unless you want to make one of them the chairperson).
The bulk of this formula should look familiar; it’s the formula for the number of permutations of n elements taken r at a time (see the previous section) — with an extra factor in the denominator. The formula is actually the permutations divided by r!.
You can also indicate combinations with two other notations:
The different notations all mean the same thing and have the same answer. For the most part, the notation you use is a matter of personal preference or what you can find on your calculator. You read all the notations as “n choose r.”
For instance, say you have tickets to the theatre, and you want to choose three people to join you. How many different ways can you choose those three people if you have five close friends to choose from? Your friends are Violet, Wally, Xanthia, Yvonne, and Zeke. You can take
- {Violet, Wally, Xanthia}
- {Violet, Wally, Yvonne}
- {Violet, Wally, Zeke}
- {Wally, Xanthia, Yvonne}
- {Wally, Xanthia, Zeke}
- {Xanthia, Yvonne, Zeke}
You find six different subsets. Is that all? Have you forgotten any?
You can check your work with the formula for the number of combinations of five elements taken three at a time:
Oops! You must have forgotten some combinations. (See the upcoming section “Drawing a tree diagram for a combination” to see what you missed.)
Branching Out with Tree Diagrams
Combinations and permutations (see the previous section) tell you how many subsets or groupings to expect within certain sets, but they don’t shine a light on what elements are in those groupings or subsets. A nice, orderly way to write out all the combinations or permutations is to use a tree diagram. The name tree diagram comes from the fact that the drawing looks something like a family tree — branching out from the left to the right. The left-most entries are your “first choices,” the next column of entries shows what you can choose next, and so on.
You can’t use tree diagrams in all situations dealing with permutations and combinations — the diagrams get too large and spread out all over the place — but you can use tree diagrams in many situations involving counting items. Tree diagrams also appear in the worlds of statistics, genetics, and other studies.
Picturing a tree diagram for a permutation
When you choose two different letters from a set of four letters to form different “words,” you can find the number of different words possible with the permutation ![]() (see the section “Arranging permutations of sets”). You can form 12 different two-letter words. To make a list of the words — and not repeat yourself or leave any out — you should create a tree diagram.
(see the section “Arranging permutations of sets”). You can form 12 different two-letter words. To make a list of the words — and not repeat yourself or leave any out — you should create a tree diagram.
Go out on a limb and follow these simple steps:
- Start out with the original set of n items and list them vertically — one under the other — leaving some space for your tree to grow to the right.
Connect the next set of entries to the first set by drawing short line segments — the branches.
You’ll need
 branches for each item.
branches for each item.Keep connecting more entries until you complete the task as many times as needed.
Each time, you decrease the number of branches by 1.
For example, say you want to create two-letter permutations out of the word “seat.” Figure 17-8 shows the tree diagram that organizes these permutations.

John Wiley & Sons, Inc.
FIGURE 17-8: Creating two-letter words (permutations) from seat.
Drawing a tree diagram for a combination
In the section “Mixing up sets with combinations,” you receive the job of choosing three friends from a set of five to accompany you to the theatre, and you find that you have ten different ways to choose them. The order in which you choose them doesn’t matter; they get to go or they don’t. The tree diagram in Figure 17-9 shows how you determine all the arrangements without repeating yourself.

John Wiley & Sons, Inc.
FIGURE 17-9: The branches of the tree diagram get smaller as you account for all the possibilities.
Because the order doesn’t matter, you first figure out all the arrangements with Violet and Wally, and then Violet and Xanthia, and then Violet and Yvonne. The number of branches decreases because you can’t repeat groupings. You then move to Wally and Xanthia and then Wally and Yvonne. You finally get to Xanthia and stop there, because you’ve accounted for all the groupings.
Do you see which sets I missed in the section “Mixing up sets with combinations”? You can easily miss some arrangements if you don’t have an orderly method for listing them. And you may be concerned that Violet has a much better chance for selection than her peers, but that isn’t the case. If you look through all ten sets of three people, you see that each name appears six times.

 When dealing with sets that have huge numbers of elements, using set builder notation can save you time and busywork. And if the pattern of elements is obvious (always a tricky word in math), you can use an ellipsis. For the set containing all the odd numbers between 0 and 100, for example, you can write
When dealing with sets that have huge numbers of elements, using set builder notation can save you time and busywork. And if the pattern of elements is obvious (always a tricky word in math), you can use an ellipsis. For the set containing all the odd numbers between 0 and 100, for example, you can write  When one set is a subset of another, and the two sets aren’t equal (meaning they don’t contain the same elements), the subset is called a proper subset, indicating that the subset has fewer elements than the superset. Technically, any set is its own subset, so you can say that a set is an improper subset of itself. You write that statement with the subset notation and a line under it to indicate “subset and, also, equal to.” To say that set B is its own subset, you write
When one set is a subset of another, and the two sets aren’t equal (meaning they don’t contain the same elements), the subset is called a proper subset, indicating that the subset has fewer elements than the superset. Technically, any set is its own subset, so you can say that a set is an improper subset of itself. You write that statement with the subset notation and a line under it to indicate “subset and, also, equal to.” To say that set B is its own subset, you write  If a set A has n elements, it has
If a set A has n elements, it has