Since the floating-point values have been discussed, it is now time to discuss some of the operations that can be performed with them, such as bit masking and comparisons.
Why would someone wish to generate a bit mask for a floating-point number? Due to the nature of the mantissa and exponential bits, a floating-point value can be manipulated.
Workbench Files:Benchx86chap14projectplatform
project | platform | |
3D (Special) | vsf3d | vc6 |
4vec (Special) | qvsf3d | vc.net |
The reciprocal and square root are two mathematical operations that have special functionality with vector processors. The division operation is typically performed by multiplying the reciprocal of the denominator by the numerator. A square root is not always just a square root; sometimes it is a reciprocal square root. So first we examine some simple forms of these.
Another way to remember this is:
The simplified form of this parallel instruction individually calculates the square root of each of the packed floating-point values, and returns the result in the destination. Some processors support the square root instruction directly, but some processors, such as the 3DNow! instruction set, actually support it indirectly through instructional stages. And some processors support it as a reciprocal square root.
So now I pose a little problem. We hopefully all know that a negative number should never be passed into a square root because computers go BOOM, as they have no idea how to deal with an identity (i.)
With that in mind, what is wrong with a reciprocal square root? Remember your calculus and limits?
Okay, how about this one?

Do you see it now? You cannot divide by zero, as it results in infinity and is mathematically problematic. So what has to be done is to trap for the x being too close to zero (as x approaches zero) and then substitute the value of one as the solution for the reciprocal square root.
y = (x < 0.0000001) ? 1.0 : (1 / sqrt(x)); // Too close to zero
It is not perfect but it is a solution. The number is so close to infinity that the result of its product upon another number is negligible. So in essence the result is that other number; thus the multiplicative identity comes to mind: 13 n = n. But how to deal with this in vectors? Well, you just learned the trick in this chapter! Remember the packed comparison? It is just a matter of using masking and bit blending. So in the case of a reciprocal square root, the square root can be easily achieved by merely multiplying the result by the original x value, thus achieving the desired square root. Recall that the square of a square root is the original value.

SSE | sqrtss xmmDst, xmmSrc/m32 | Single-precision | 128 |
This SIMD instruction is a 128-bit scalar operation that calculates the square root of only the lowest single-precision floating-point element containing the scalar xmmSrc. The result is stored in the lowest single-precision floating-point block at destination xmmDst, and the remaining bit blocks are left intact.

SSE | sqrtps xmmDst, xmmSrc/m128 | Single-precision | 128 |
This SIMD instruction is a 128-bit parallel operation that calculates the square root of the four single-precision floating-point blocks contained within xmmSrc, and stores the result in the single-precision floating-point blocks at destination xmmDst.

SSE2 | sqrtsd xmmDst, xmmSrc/m64 | Double-precision | 128 |
This SIMD instruction is a 128-bit scalar operation that calculates the square root of only the lowest double-precision floating-point block containing the scalar xmmSrc, and stores the result in the lowest double-precision floating-point block at destination xmmDst. The remaining bit blocks are left intact.
SSE2 | sqrtpd xmmDst, xmmSrc/m128 | Double-precision | 128 |
This SIMD instruction is a 128-bit parallel operation that calculates the square root of the two double-precision floating-point blocks contained within xmmSrc, and stores the result in the double-precision floating-point blocks at destination xmmDst.
3DNow! | pfrsqrt mmxDst, mmxSrc/m32 | Single-precision | 32/64 |
SSE | rsqrtss xmmDst, xmmSrc/m32 | Single-precision | 32 |
rsqrtps xmmDst, xmmSrc/m128 | Single-precision | 128 |
This SIMD instruction is a 32-bit scalar operation that calculates the square root of only the lowest single-precision floating-point block containing the scalar mmSrc, and stores the duplicate result in the low and high single-precision floating-point blocks at destination mmDst.
A square root is time consuming and should be omitted whenever possible. If it is indeed needed, then the next logical choice would be between an imprecise and quick calculation or a more accurate but slower calculation. The following code is for a simple 15-bit accuracy scalar square root ![]() supported by the 3DNow! instruction set.
supported by the 3DNow! instruction set.
movd mm0,fA ; {0 fA}
mov edx,pfD ; float destinationA fast version of the previous instruction would entail taking advantage of the two-stage vector instructions PFRSQIT1 and PFRCPIT2, in conjunction with the result of the square root instruction PFRSQRT, to achieve a higher 24-bit precision. It uses a variation of the Newton-Raphson reciprocal square root approximation.
Mnemonic | P | PII | K6 | 3D! | 3Mx+ | SSE | SSE2 | A64 | SSE3 | E64T |
|---|---|---|---|---|---|---|---|---|---|---|
PFRCPIT2 |
|
|
| |||||||
PFRSQIT1 |
|
|
|
First stage for 24-bit reciprocal:
3DNow! pfrsqit1 mmxDst, scalar(mmx/m32) Single-precision 64
Second stage for 24-bit reciprocal and/or square root (see reciprocals in Chapter 13):
3DNow! pfrcpit2 mmxDst, scalar(mmx/m32) Single-precision 64
The following is the same as the previous scalar square root algorithm but is coded for 24-bit precision. Note the addition of the PFRSQIT1 and PFRCPIT2 instructions.
mov edx,pfD ; (float) destination
For SSE it is merely a scalar square root instruction.
Are you nuts? Vector square roots? What are you thinking?
Unless you have a top-of-the-line supercomputer, I would recommend you stay away from vector square roots. Instead, you will typically only need a single square root. If you really need vector-based square roots, remember that your processor can only do one at a time and your code will have to wait for it to complete before issuing a request to begin the next one. That could take almost forever! Well, not quite. But it is still not a great idea. Also, do not forget about preventing negative numbers from being processed by a square root. That causes exception faults!
Example 14-6. ...chap14qvsf3dQVsf3D.cpp
void vmp_QVecSqrt(vmp3DQVector * const pvD,
const vmp3DQVector * const pvA)
{
pvD->x = sqrtf(pvA->x);
pvD->y = sqrtf(pvA->y);
pvD->z = sqrtf(pvA->z);
pvD->w = sqrtf(pvA->w);
}Similar to an estimated reciprocal for a division, a square root sometimes is available as an estimate as well. Be warned that the estimated square root is faster but has a lower precision. But if the lower precision is viable for your application, then investigate using the estimated square root instead.
The 3DNow! instruction set supports 64-bit so two loads must be handled simultaneously as well as two saves, but it is a simple matter of adding the two pairs of floats to each other.
mov eax,vA ; Vector A
mov edx,vD ; Vector destinationIn the previous code there is a comment in bold related to insertion for 24-bit precision. By inserting the following code the higher accuracy will be achieved. It uses the Newton-Raphson reciprocal square approximation.
For SSE there is a 24-bit precision quad square root. For unaligned memory, substitute MOVUPS for the MOVAPS.
Ever hear that the shortest distance between two points is a straight line? The square of the hypotenuse of a right triangle is equal to the square of each of its two sides whether in 2D or 3D space. The Pythagorean equation is essentially the distance between two points, in essence the magnitude of their differences.
The first rule of a square root operation is to not use it unless you really have to as it is a time intensive mathematical operation. One method typically used for calculating the length of a line between two points whether it exists in 2D or 3D space is to use the Pythagorean equation.
2D Distance
3D Distance

Figure 14-2. Right triangle within 3D Cartesian coordinate system representing a 3D distance and thus its magnitude
Mathematical Formula:

So if the dot product dp = x2+ y2+ z2approaches zero, the value of 1/x gets closer to infinity. Once x becomes zero, the solution becomes undefined: 1/0 = ∞. When a number is extremely close to infinity and is passed to a square root, the accuracy becomes lost. So instead of being forced to divide by zero (1/0) to represent infinity, it is instead set to a value of one (y x 1 = y); thus the original value is preserved.
The Pythagorean equation is the distance between two points, in essence, the magnitude of their differences. In a terrain-following algorithm for creature AI, the distance between each of the creatures and the main character would be compared to make an idle, run, or flee determination. The coordinates of each object are known but their distances would have to be calculated and then compared to each other as part of a solution. Let's examine a simplistic equation utilizing r to represent the distance between the player and four monsters {mA through mD}:

If you remember the algebraic law of multiplicative identity, the square root factors out of the equation, as it can be removed from both sides of the equal sign and the equation will remain in balance.
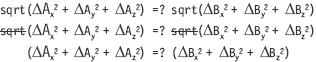
Does this look a little similar to the sum of absolute differences operation discussed in Chapter 7? They are different by the sum of absolutes versus the sum of the squares, but they nevertheless have a similarity. The point is that there is no need to use the square root operation each time in this kind of problem. Neat, huh! It is an old trick but still an effective one.
Now supposing that it has been discovered that Monster C is the closest monster. Take the square root to calculate the distance, not forgetting to use the estimate square root version if accuracy is unnecessary.
The 3DNow! instruction set supports 64-bit so two loads and/or stores must be handled simultaneously, but the result is a simple matter of adding the two pairs of floats to each other.
mov eax,vA ; Vector A
mov edx,vD ; Vector destination
















