There are multitudes of variations of multiplicative mnemonic manipulations. It seems almost every processor supports a slightly different scheme involving different integer word sizes, floating-point precision types, methods of rounding, with saturations, etc. Fundamentally, despite its variations, it is very similar to and uses the same methodologies as the addition detailed in the last chapter.
Notice the integer multiplication examples below. The example on the left requires more bits to contain the results of the operation and thus different methods have been implemented to reduce that value to its component size. The results of the floating-point multiplication in the other two examples follow the rules of the IEEE-754 standard for binary floating-point arithmetic. The result of a multiplication is stored with no increase in data containment size, but there is a penalty of a loss of precision.

Workbench Files:Benchx86chap13projectplatform
project | platform | |
|---|---|---|
3D (Mul/Div) | vmd3d | vc6 |
4vec (Mul/Div) | qvmd3d | vc.net |
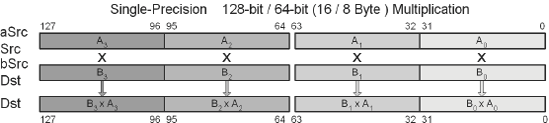
3DNow! | pfmul | mmxDst, mmxSrc | Single-precision | 64 |
SSE | mulps | xmmDst, xmmSrc/m128 | Single-precision | 128 |
This SIMD instruction uses a 64 (128)-bit data path and so two (four) operations occur in parallel. The product is calculated for each of the Real32 single-precision floating-point elements of the multiplicand xmmDst and the multiplier xmmSrc for each block, and the result is stored in each of the original Real32 elements of the destination xmmDst.

SSE2 | mulpd xmmDst, xmmSrc/m128 | Double-precision | 128 |
This vector instruction uses a 128-bit data path and so two operations occur in parallel. The product is calculated for each of the Real64 (double-precision floating-point) pairs of the multiplicand xmmDst and the multiplier xmmSrc for each block, and the result is stored in each of the original Real64 elements of the destination xmmDst.
SSE | mulss xmmDst, xmmSrc/m32 | Single-precision | 32 |
This vector instruction uses a 128-bit data path and only the first Real32 (single-precision floating-point) source scalar multiplier and the multiplicand xmmDst, and the result is stored in the original Real32 elements of the destination xmmDst.
SSE2 | mulsd xmmDst, xmmSrc/m64 | Double-precision | 64 |
This vector instruction uses a 128-bit data path and only the first Real64 (double-precision floating-point) source scalar multiplier and the multiplicand xmmDst, and the result is stored in the original Real64 elements of the destination xmmDst.
Vector floating-point multiplication is one of the mathematical equations that you will tend to use the most in your video games whether as a tri or quad float vector.
The multiplication of vectors is similar to that of the addition of vectors.
The multiplication-add (MADD) is merely a multiplication followed by a summation. Some processors, such as AltiVec, do not support a stand-alone multiplication, some support only the multiplication-add, and some support both. But it is much more efficient to call a MADD-type instruction when appropriate, instead of separately.
Now examine these functions closer using x86 assembly. 3DNow! supports 64-bit data so two loads must be handled simultaneously as well as two stores, but it is a simple matter of adding the two pairs of floats to each other.
mov eax,vA ; Vector A mov ebx,vB ; Vector B mov edx,vD ; Vector Destination
Example 13-5. ...chap13vmd3dVmd3DX86M.asm
movq mm0,[ebx] ; vB.xy {By Bx}
movq mm1,[eax] ; vA.xy {Ay Ax}
movd mm2,(vmp3DVector PTR [ebx]).z ; {0 Bz}
movd mm3,(vmp3DVector PTR [eax]).z ; {0 Az}
pfmul mm1,mm0 ; {AyBy AxBx}
pfmul mm3,mm2 ; { 0 AzBz}
movq [edx],mm1 ; {AyBy AxBx}
movd (vmp3DVector PTR [edx]).z,mm3 ; { AzBz}As you may have noticed, the vector only loaded one float instead of two, set the second to zero, calculated the product, and then wrote the three values back to memory.
For MADD, the addition needs to be handled separately.
Example 13-7. ...chap13qvmd3dQVmd3DX86M.asm
mov ecx,vC ; Vector C
movq mm0,[ebx+0] ; vB.xy {By Bx}
movq mm1,[eax+0] ; vA.xy {Ay Ax}
movq mm4,[ecx+0] ; vC.xy {Cy Cx}
movq mm2,[ebx+8] ; vB.zw {Bw Bz}
movq mm3,[eax+8] ; vA.zw {Aw Az}
movq mm5,[ecx+8] ; vC.zw {Cw Cz}
pfmul mm1,mm0 ; {AyBy AxBx}
pfmul mm3,mm2 ; {AwBw AzBz}
pfadd mm1,mm4 ; {AyBy+Cy AxBx+Cx}
pfadd mm3,mm5 ; {AwBw+Cw AzBz+Cz}
movq [edx+0],mm1 ; {AyBy+Cy AxBx+Cx}
movq [edx+8],mm3 ; {AwBw+Cw AzBz+Cz}The SSE processor in the following code snippet can load 128 bits at a time, so the entire 96-bit vector can be loaded at once, including an extra 32 bits. This introduces a problem of contamination when the 96-bit value is written to memory as 128 bits. The solution is to read those destination bits, preserve the upper 32 bits through bit masking and blending, and write the newly merged 128 bits. Keep in mind efficient memory organization and memory tail padding as discussed earlier. Data can be misaligned or aligned, but 128-bit alignment is preferable. Only aligned memory will be discussed, but for SSE keep in mind the use of MOVUPS instead of MOVAPS when memory alignment cannot be guaranteed.
Example 13-8. ...chap13vmd3dVmd3DX86M.asm
movapsxmm2,[edx] ; vD.###w {Dw # # #}movapsxmm1,[ebx] ; vB.xyz# {# Bz By Bx}movapsxmm0,[eax] ; vA.xyz# {# Az Ay Ax} andps xmm1,OWORD PTR lomsk96 ; {0 Az Ay Ax} andps xmm2,OWORD PTR himsk32 ; {Dw 0 0 0} mulps xmm0,xmm1 ; {## AzBz AyBy AxBx} andps xmm0,OWORD PTR lomsk96 ; limit -0 orps xmm0,xmm2 ; {Dw AzBz AyBy AxBx}movaps[edx],xmm0 ; {Dw AzBz AyBy AxBx}
For MADD, the summation is an appended instruction as compared to the previous vector multiplication.
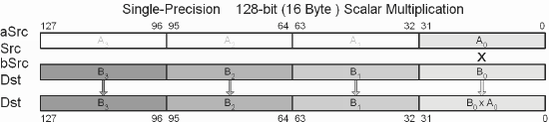
The scalar multiplication of vectors is also a relatively simple matter for vector math instructions to handle, just like the scalar addition and subtraction of vectors. The trick is to replicate the scalar so it appears like a second vector.
This function multiplies a scalar with each element of a vector. A scalar has multiple uses but the primary is in the use of "scaling" a vector. A scalar of one would result in the same size. Two would double the length of the vector, etc.
mov eax,vA ; Vector A mov edx,vD ; Vector destination
The 32-bit scalar is unpacked into a pair and then treated similar to the vector multiplication of two vectors.
The SSE version of the code is changed from a 64-bit load to a 128-bit load, but the principles remain the same.
Example 13-14. ...chap13vmd3dVmd3DX86M.asm
pxor xmm1,xmm1 ; {0 0 0 0}
movss xmm1,fScalar ; {0 0 0 s}
movaps xmm2,[edx] ; {Dw # # #}
movaps xmm0,[eax] ; vA.xyz# {# Az Ay Ax}
shufps xmm1,xmm1,11000000b ; 3 0 0 0 {0 s s s}
andps xmm2,OWORD PTR himsk32 ; {Dw 0 0 0}
mulps xmm0,xmm1 ; {# Azs Ays Axs}
andps xmm0,OWORD PTR lomsk96 ; {0 Azs Ays Axs}
orps xmm0,xmm2 ; {Dw Azs Ays Axs}
movaps [edx],xmm0 ; {Dw Azs Ays Axs}A dot product, also known as an inner product, of two vectors is the summation of the results of the product for each of their {XYZ} elements, thus resulting in a scalar. Not to oversimplify it, but this scalar is equal to 0 if the angle made up by the two vectors are perpendicular (=90°), positive if the angle is acute (<90°), and negative if the angle is obtuse (>90°).
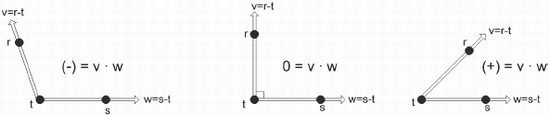
Figure 13-1. Dot product (inner product). A positive number is an acute angle, zero is perpendicular, and negative is an obtuse angle.
These are vectors that produce a scalar defined by v · w when their products are combined. The dot product is represented by the following equation:
The equation resolves to the following simplified form:
So as we have learned, we first write it in a high-level language before writing it in assembly code.
Example 13-16. ...chap13vmd3dVmd3D.cpp
void vmp_DotProduct(float * const pfD,
const vmp3DVector * const pvA,
const vmp3DVector * const pvB)
{
*pfD = pvA–>x * pvB–>x
+ pvA–>y * pvB–>y
+ pvA–>z * pvB–>z;
}This is one of my favorite equations because it does not slice, dice, or chop, but it culls, it illuminizes, it simplifies, it cosineizes (not a real word, but you know what I mean). It is the Sledge-O-Matic!!! Well, not quite comedian Gallagher's watermelon disintegration kitchen utensil, but it does do many things and so it is just as useful.
From Figure 13-1 you will note that if the resulting scalar value is positive (+), the vectors are pointing in the same general direction. If zero (0), they are perpendicular to each other, and if negative (–), they are pointed in opposite directions.
Before explaining further it should be pointed out that to keep 3D graphic algorithms as simple as possible the three vertices for each polygon should all be ordered in the same direction. For example, by using the left-hand rule and keeping all the vertices of a visible face in a clockwise direction, such as in Figure 13-2, back face culling will result. If all visible face surfaces use this same orientation, then if the vertices occur in a counterclockwise direction they are back faced and thus pointing away and need not be drawn, saving render time.
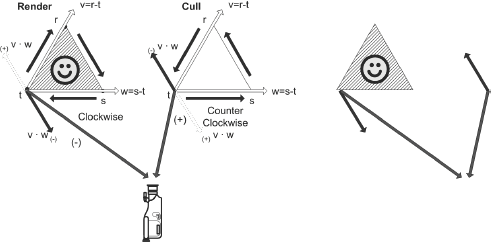
Figure 13-2. Face culling mechanism where if the angle between the camera and the perpendicular to the face plane is obtuse, then the face is pointed away from the camera and can be culled.
Contrarily, if polygons are arranged in a counterclockwise orientation, then the inverse occurs where a positive value is drawn and a negative value is culled. Keep in mind, however, that most software algorithms keep things in a clockwise orientation.
By calculating the dot product of the normal vector of the polygon with a vector between one of the polygon's vertices and the camera, it can be determined if the polygon is back facing and needs to be culled. A resulting positive value indicates that the face is pointed away, hence back facing and can be culled and not rendered. A negative value indicates a face oriented toward the camera and thus visible.
Another use for the dot product equation is that it is also the cosine of the angle. The cosine is returned by dividing the dot product by the product of the magnitudes of the two vectors. Note that v and w are vectors and that |v| and |w| are their magnitudes.

And using standard trigonometric formulas, such as:
...sine and other trigonometric results can be calculated.
So the good stuff is yet to come!
The 3DNow! instruction set uses the 64-bit MMX registers, but 64-bit memory alignment cannot be guaranteed. In this case, it is typically better to handle memory access as individual 32-bit floats then to unpack into 64-bit pairs, process, then save individually as 32 bit. The PFACC instruction is unique as it allows the hi/lo 32 bits to be summed with each other, within each of the vectors.
Example 13-17. ...chap13vmd3dVmd3DX86M.asm
mov ebx,vB ; Vector B
mov eax,vA ; Vector A
mov edx,vD ; Vector destination
movd mm0,(vmp3DVector PTR [ebx]).z ; {0 Bz}
movd mm1,(vmp3DVector PTR [eax]).z ; {0 Az}
movq mm2,[ebx] ; {By Bx}
movq mm3,[eax] ; {Ay Ax} pfmul mm0,mm1 ; {00 BzAz}
pfmul mm2,mm3 ; {ByAy BxAx}
pfacc mm2,mm2 ; {ByAy+BxAx ByAy+BxAx}
pfadd mm0,mm2 ; {ByAy+BxAx+0 ByAy+BxAx+BzAz}
movd [edx],mm0 ; Save {ByAy+BxAx+BzAz}The SSE instruction loads the 96-bit vector value using a 128-bit XMM register. The operation entails the multiplication of the {XYZ} pairs from both vectors. The data is swizzled to allow scalar additions, and then the 32-bit single-precision float scalar result is written to memory.
Example 13-18. ...chap13vmd3dVmd3DX86M.asm
movapsxmm1,[ebx] ; vB.xyz# {# Bz By Bx}movapsxmm0,[eax] ; vA.xyz# {# Az Ay Ax} mulps xmm0,xmm1 ; {A#B# AzBz AyBy AxBx} movaps xmm1,xmm0 movaps xmm2,xmm0 unpckhps xmm0,xmm0 ; {A#B# A#B# AzBz AzBz} shufps xmm1,xmm1,11100001b ; {A#B# AzBz AxBx AyBy} addss xmm2,xmm0 ; {A#B# AzBz AxBx AzBz+AxBx} addss xmm2,xmm1 ; {A#B# AzBz AxBx AzBz+AxBx+AyBy} movss [edx],xmm2 ; Save {AzBz+AxBx+AyBy}
A cross product, also known as the outer product, of two vectors is a third vector perpendicular to the plane of the two original vectors. The two vectors define two sides of a polygon face and their cross product points away from that face.
v ={v1, v2, v3} and w = {w1, w2, w3} are vectors of a plane denoted by matrix R3. The cross product is represented by the following equation:
The standard basis vectors are i=(1,0,0) j=(0,1,0) k=(0,0,1).
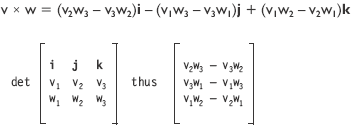
The equation resolves to the following simplified form:
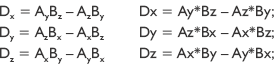
Note the following simple vector structure is actually 12 bytes, which will pose a data alignment problem for SIMD operations.
One method is to use individual single-precision floating-point calculations, of which you may already be familiar. With this in mind, examine the following simple C language function to implement it. Note the use of the temporary floats x, y to prevent the resulting solutions of each field {x,y,z} from affecting either source pvA or pvB in the case where the destination pvD is also a source.
Example 13-19. ...chap13vmd3dVmd3D.cpp
void vmp_CrossProduct(vmp3DVector* const pvD,
const vmp3DVector* pvA, const vmp3DVector* pvB)
{
float x, y;
x = pvA–>y * pvB–>z – pvA–>z * pvB–>y;
y = pvA–>z * pvB–>x – pvA–>x * pvB–>z;
pvD–>z = pvA–>x * pvB–>y – pvA–>y * pvB–>x;
pvD–>x = x;
pvD–>y = y;
}The 3DNow! instruction set uses the 64-bit MMX registers, but 64-bit memory alignment cannot be guaranteed. In this case it is typically better to handle memory access as individual 32-bit floats than to unpack into 64-bit pairs, process, then save individually as 32 bit. This example is kind of big so there are extra blank lines to help separate the various logic stages and it is not optimized to make it more readable.
Example 13-20. ...chap13vmd3dVmd3DX86M.asm
mov ebx,vB ; Vector B
mov eax,vA ; Vector A
mov edx,vD ; Vector destination
movd mm0,(vmp3DVector PTR [ebx]).x ; vB.x {0 Bx}
movd mm1,(vmp3DVector PTR [ebx]).y ; vB.y {0 By}
movd mm2,(vmp3DVector PTR [ebx]).z ; vB.z {0 Bz}
movd mm3,(vmp3DVector PTR [eax]).x ; vA.x {0 Ax}
movd mm4,(vmp3DVector PTR [eax]).y ; vA.y {0 Ay}
movd mm5,(vmp3DVector PTR [eax]).z ; vA.z {0 Az}
pfmul mm4,mm0 ; vB.xy {0 AyBx}
punpckldq mm0,mm1 ; {By Bx}
movd mm1,(vmp3DVector PTR [eax]).y ; vA.y {Ay}
movd mm6,(vmp3DVector PTR [ebx]).y ; vB.y {By}
punpckldq mm2,mm2 ; {Bz Bz}
punpckldq mm3,mm1 ; {Ay Ax}
punpckldq mm5,mm5 ; {Az Az}
pfmul mm2,mm3 ; vA.xy {BzAy BzAx}
pfmul mm5,mm0 ; vB.xy {AzBy AzBx}
pfmul mm6,mm3 ; vA.xy {0Ay ByAx}
movq mm7,mm2 ; {BzAy BzAx}
pfsub mm2,mm5 ; {BzAy–AzBy BzAx–AzBx}
psrlq mm2,32 ; x@ {0 BzAy–AzBy}
pfsub mm5,mm7 ; y@ {AzBy–BzAy AzBx–BzAx}
pfsub mm6,mm4 ; z@ {0–0 ByAx–AyBx}
movd (vmp3DVector PTR [edx]).x,mm2 ; x=AyBz–AzBy
movd (vmp3DVector PTR [edx]).y,mm5 ; y=AzBx–AxBz
movd (vmp3DVector PTR [edx]).z,mm6 ; z=AxBy–AyBxIf you examine it closely you will notice the operations performed within each block and how they correlate to the generic C code that was provided.
The SSE instruction set uses the 128-bit XMM registers with MOVUPS instead of MOVAPS for unaligned memory. This function has also been unoptimized so as to make it more readable.
Example 13-21. ...chap13vmd3dVmd3DX86M.asm
movapsxmm1,[ebx] ; vB.xyz# {# Bz By Bx}movapsxmm0,[eax] ; vA.xyz# {# Az Ay Ax} ; Crop the 4th(w) field andps xmm1,OWORD PTR lomsk96 ; {0 Bz By Bx} andps xmm0,OWORD PTR lomsk96 ; {0 Az Ay Ax} movaps xmm5,xmm1 movaps xmm6,xmm0 shufps xmm1,xmm1,11010010b ; 3 1 0 2 {0 By Bx Bz} shufps xmm0,xmm0,11001001b ; 3 0 2 1 {0 Ax Az Ay} shufps xmm6,xmm6,11010010b ; 3 1 0 2 {0 Ay Ax Az} shufps xmm5,xmm5,11001001b ; 3 0 2 1 {0 Bx Bz By}movapsxmm2,[edx] ; Get destination {Dw # # #} mulps xmm1,xmm0 mulps xmm5,xmm6 andps xmm2,OWORD PTR himsk32 ; {Dw 0 0 0} subps xmm1,xmm5 ; { 0 z y x} orps xmm1,xmm2 ; [Dw z y x}movups[edx],xmm1 ; vD.wxyz {Dw z y x}

It was discussed in a previous chapter that a difference is the summation of a term and the inverse of a second term using the additive inverse algebraic law. A division is also a play on an equation transformation: a multiplication of the dividend by the reciprocal of the divisor.
Some instruction sets, such as 3DNow!, do not directly support floating-point division but do support the product of a reciprocal.
SSE | divps xmmDst, xmmSrc/m128 | Single-precision | 128 |
This vector instruction uses a 128-bit data path and so four operations occur in parallel. The result is calculated for each of the source Real32 (single-precision floating-point) quads of the quotient xmmDst and the divisor xmmSrc of each block, and the result is stored in each of the original Real32 elements of the destination xmmDst.

SSE2 | divpd xmmDst, xmmSrc/m128 | Double-precision | 128 |
This vector instruction uses a 128-bit data path and so two operations occur in parallel. The result is calculated for each of the source Real64 (double-precision floating-point) pairs of the quotient xmmDst and the divisor xmmSrc of each block, and the result is stored in each of the original Real64 elements of the destination xmmDst.
SSE | divss xmmDst, xmmSrc/m32 | Single-Precision | 32 |
This scalar instruction uses a 128-bit data path but only the least significant Real32 (single-precision floating-point) elements are used — the xmmSrc source scalar divisor and the xmmDst quotient. The result is stored in the lower 32 bits of the destination xmmDst, leaving the upper 96 bits unaffected.
SSE2 | divsd xmmDst, xmmSrc/m64 | Double-precision | 64 |
This scalar instruction uses a 128-bit data path and only the first Real64 (double-precision floating-point) source scalar divisor and the quotient xmmDst. The result is stored in the original lower 64 bits of the destination xmmDst, leaving the upper 64 bits unaffected.
SSE | rcpps xmmDst, xmmSrc/m128 | Single-precision | 128 |
SSE | rcpss xmmDst, xmmSrc/m32 | Single-precision | 128 |
The RCPPS instruction uses a packed 128-bit data path and each source xmmDst element and divides it by each xmmSrc divisor, produces the reciprocal, and stores the result in destination xmmDst.
The RCPSS scalar instruction uses a 128-bit data path. It takes the least significant Real32 in source xmmDst, divides it by the least significant Real32 in xmmSrc divisor, produces the reciprocal, and stores the result in destination xmmDst.
3DNow! | pfrcp mmxDst, mmxSrc/m32 | Single-precision | 32/64 |
This 3DNow! scalar instruction uses a 64-bit data path. It takes only the first Real32 (single-precision floating-point) source scalar divisor, produces the 14-bit reciprocal, and stores the result in both the lower 32 bits and upper 32 bits of the destination mmxDst.
To convert the result to a division it only needs to be followed up by the multiplication instruction PFMUL. This instruction would be considered a low precision division.
A division, whether it has a 1/x or a/b orientation, is time consuming. Whenever possible, a multiplication of a reciprocal value should be used instead. If that is not possible, then the next logical method would be making a choice between an imprecise and quick calculation or a more accurate but slower calculation. The following code is for a simple 14-bit accuracy scalar division D=A÷B supported by the 3DNow! instruction set.
Note that the code has the fast precision set to 0.001f to accommodate SSE, but 0.0001f works for 3DNow! estimation.
A fast version of the previous instruction would entail taking advantage of the two-stage vector instructions PFRCPIT1 and PFRCPIT2, in conjunction with the result of the reciprocal instruction PFRCP, to achieve a higher 24-bit precision. It uses a variation of the Newton-Raphson reciprocal square approximation.
This is an error correcting scheme to infinitely reduce the error, but typically only a single pass is used. Not to simplify it, but this typically involves calculating the product of the estimated square root, finding the difference from the original number, then adjusting by that ratio.
Mnemonic | P | PII | K6 | 3D! | 3Mx+ | SSE | SSE2 | A64 | SSE3 | E64T |
|---|---|---|---|---|---|---|---|---|---|---|
PFRCPIT1 |
|
|
| |||||||
PFRCPIT2 |
|
|
|
First stage for 24-bit reciprocal:
3DNow! | pfrcpit1 mmxDst, mmxSrc/m32 | Single-precision | 64 |
Second stage for 24-bit reciprocal and/or square root:
3DNow! | pfrcpit2 mmxDst, mmxSrc/m32 | Single-precision 64 |
The following is the same as the previous scalar division algorithm but is coded for 24-bit precision. Note the addition of the PFRCPIT1 and PFRCPIT2 instructions. Note the following code is not optimized so as to make it more readable.
The SSE version merely reads the floats as scalars, divides them as scalars, and stores the scalar result.
The vector and quad vector operations are not much different. The scalar in essence becomes replicated into all the denominator fields and then the product of the reciprocals (division) takes place.
Now examine these functions closer using x86 assembly. As MMX does not support floating-point only, 3DNow! and SSE can be utilized. 3DNow! supports 64-bit so two loads must be handled simultaneously. The functionality is, in essence, a reciprocal of the scalar is calculated and mirrored into each of the denominator positions, and the product is calculated with the original vector with the result stored. These examples are all quad vectors, and special consideration must be taken when dealing with three float vectors to preserve the {W} float element.
movd mm2,fScalar ; {0 s}
mov eax,vA ; Vector A
mov edx,vD ; Vector destinationThe following code is unoptimized to make it more readable. Notice in the standard precision the second- and third-stage reciprocal instructions are used.
Example 13-27. ...chap13qvmd3dQVmd3DX86.asm
pfrcp mm3,mm2 ; {1/s 1/s} 14-bit
punpckldq mm2,mm2 ; { s s}
pfrcpit1 mm2,mm3 ; {1/s 1/s}
pfrcpit2 mm2,mm3
movq mm0,[eax+0] ; vAxy {Ay Ax}
movq mm1,[eax+8] ; vAzw {Aw Az}
pfmul mm0,mm2 ; {Ay × 1/s Ax × 1/s}
pfmul mm1,mm2 ; {Aw × 1/s Az × 1/s}
movq [edx+0],mm0 ; {Ay/s Ax/s}
movq [edx+8],mm1 ; {Aw/s Az/s}Example 13-28. ...chap13qvmd3dQVmd3DX86M.asm
movaps xmm0,[eax] ; vAxyzw {Aw Az Ay Ax}
movss xmm1,fScalar ; {0 0 0 s}
shufps xmm1,xmm1,00000000b ; 0 0 0 0 {s s s s}
divps xmm0,xmm1 ; {Aw/s Az/s Ay/s Ax/s}
movaps [edx],xmm0 ; {Aw/s Az/s Ay/s Ax/s}It is fairly simple. Similar to a scalar multiplication, the scalar is merely distributed to each of the elements of the denominator and then the division takes place. (Have you read this enough times yet?)
What is an "inner product"?
A cross product is known by another name. What is it?
What happens to a vector if a negative scalar is applied as a product?
What is the solution for:
a) A B + C D, if A = 2, B = 5, C = 3, and D = 4?
b) A = B = C = D = 0x80000000?
c) With saturation?
d) Without saturation?
What is the equation for a dot product?
Given the two vertices v:{–8, 4, –6, 4} and w:{8, 2, –6, 8}, resolve
a) v + w
b) vw
c) v · w
d) v × w