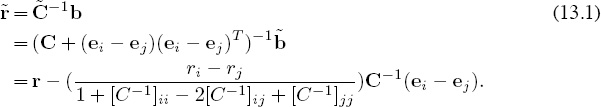Chapter Thirteen

“What If . . .” Scenarios and Sensitivity

It is common for coaches and fans to conduct “what if” analysis at certain crucial points in a season. For example, with just one game left in the season, a college football coach may wonder what happens to his team’s ranking if his team wins by β points in this final contest. Of course, one way to answer the coach’s question is to compute the ranking prior to the game of interest, then assume the coach’s desired outcome for this final game and recompute the ranking. However, for very large (think web-sized) applications, a full recomputation of the ranking for each “what if” scenario is unreasonable or even impossible. And besides, full recomputation is akin to brute force and just isn’t very elegant to a mathematician. So, in this chapter, we use the mathematical tool of perturbation analysis to precisely answer such questions with minimal additional computation.

The Impact of a Rank-One Update

In this section, we use tools from perturbation analysis to quantify the effect that a small change in the season’s data can have on Colley rankings. With a season in progress, at some point, a coach begins to speculate on his team’s playoff chances. At the current time in the season, we compute the Colley rating. Then we assume the coach’s desired outcome in his next match and recompute the rating vector. The coach’s speculation about his next game is represented as a perturbation to the coefficient matrix of the Colley system. We will study a specific type of perturbation, called a rank-one update. Rank-one updates are the simplest type of update to a matrix, and thus, make a nice starting point for our analysis. The formulas derived in this section only need to be modified slightly for updates of higher rank. In summary, we will compare the pre-perturbation rating to the post-perturbation rating. Finally we note that similar results can be derived for most other methods, yet to avoid redundancy we use just one method, the Colley method, to make our main points regarding “what if” analysis.

The tools of perturbation analysis enable us to precisely examine the effect of the coach’s speculative scenario. Let C and b be the Colley matrix and right-hand side vector before the perturbation and let and represent the Colley matrix and right-hand side vector after the perturbation. Suppose the coach wonders what happens when his team, team j, beats team i in the upcoming game. Then the perturbed matrix is related to the pre-perturbation matrix C by the formula = C + (e_i − e_j)(e_i − e_j)^T. Using the Sherman-Morrison rank-one update formula [54] and some M-matrix properties of the Colley matrix, we can express in terms of C. Specifically,

We draw three conclusions from the above equation.

• A single additional game can affect the ratings of every team. This is because the i^th and j^th columns of C⁻¹ are almost always completely dense.

• Suppose, before the perturbation, that team i was ranked above team j so that r_i − r_j > 0. Then, as expected, with the additional event of an upset of team j over team i, the rating of team i, _i, drops while the rating of team j, _j, rises. This is a consequence of the diagonal dominance and nonnegativity of C⁻¹.

• If C⁻¹ is available, then we can just pick a few elements from it in order to form . With in hand, we know precisely how each team’s rating changes as a result of the perturbation, and thus, can answer any “what if” question about any pair of teams.

To consider multiple “what if” scenarios simultaneously, a similar analysis is conducted with rank-k updates instead of the simpler rank-one update.

Sensitivity

“What if” scenarios are actually related to the mathematical concept of sensitivity. In mathematics, we call a method sensitive if small changes in the input data create large changes in the output data. We prefer insensitive or robust methods. A sensitive ranking method may give erratic rankings after an upset. This was precisely the conclusion in [21], where a tractable but practically unlikely “perfect season” (a season that contains no upsets) is considered. In other words, in a perfect season some team will go undefeated, followed by a team that loses only to the undefeated team yet beats every other team, while a third team loses to these two teams but beats all remaining teams, and so on. If the data for a season follows this structure, then, of course, the ranking of the teams is clear. While perfect seasons are extremely rare, they create data that can be mathematically analyzed with closed form expressions [21]. In many ways, the perfect season is the most well-behaved of all input seasons. If a ranking method shows signs of sensitivity on this season, then its sensitivity problems will only be exacerbated in the more realistic case of imperfect seasons.

The study in [21] analyzed the sensitivity of the Colley, Massey, and Markov ranking methods applied to the perfect season, and the results revealed good news for the Colley and Massey methods. Both were found to be insensitive to small rank-one changes to the system, with the Massey being particularly insensitive. On the other hand, the Markov method was shown to be sensitive to small rank-one changes to the system. One particular event from the 2008 NFL season was pointed to that highlighted Markov’s sensitivity on an imperfect season. This event occurred when last place Cleveland at rank 32 upset the 17-ranked NY Giants on 10/13/2008 during the Monday Night game. Comparisons of the Colley, Massey, and Markov rankings both before and after the Monday Night event are shown below.

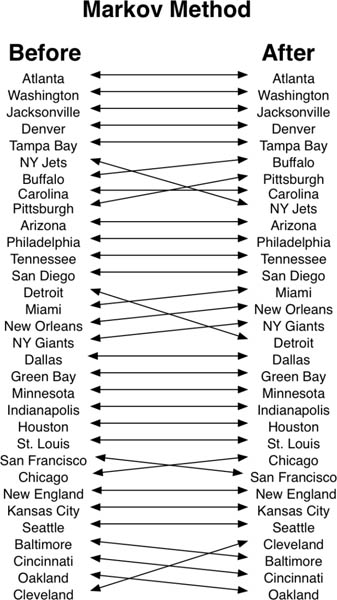
As expected, with the insensitive Colley and highly insensitive Massey methods, Cleveland rose and the Giants fell a few positions in rank as a result of the upset. However, the Markov method had the Giants moving up one position despite its loss to last place Cleveland. The Markov method’s display of such odd behavior on this event from an imperfect NFL season is consistent with the theoretical results that had established for the perfect season. More specifically, the conclusion in [21] was was that the Markov method is sensitive to events that involve teams in the tail of the rating distribution—Cleveland was the caboose of this tail in our NFL example. And because Markov ratings are known to follow a power law distribution [58], there are many teams in the tail. One might think that the method’s sensitivity would make it suspect, yet the Markov method was at the heart of Google’s original method for ranking webpages.

ASIDE: Upsets and the Markov Method’s Sensitivity