Chapter 9
Methods Based on Models for Domain Knowledge
9.1 Correction with Data Modifying Rules
Domain experts who are familiar with a recurring statistical analyses acquire knowledge about errors that are typical for that process. This knowledge is often put to use by writing data processing scripts, for example, in SQL, R, or Python that modify the data to accommodate for such errors. The statements in these scripts can be fairly simple, and in fact they are often a sequence of rules that can be stated as
The aim of each such statement is to resolve an error (detected in the condition) for which an obvious solution or other amendment can be found. Some examples of data modifying rules that we have encountered in practice include the following:
- If total revenues per total employees (in full-time equivalent) is less than 1000, all variables from the income slate must be divided by 1000.
- If other staff costs is less than zero, replace with its absolute value.
- If general expenditures exceeds one half of total expenditures, then total other expenditures is set to missing.
In the last case, a value is set to missing so that a better value can later be estimated by an imputation method.
This method of data correction is a common practice and may have a significant effect on the final results. In a study of Pannekoek et al. (2014), the effect of various data cleaning steps on two different multistep data cleaning processes was investigated. It was found that of all cells that were altered during the process, a majority was touched by data modifying rules. It was also shown that the change in mean value for some key variables may change significantly by application of such rules, for example, because they may correct for unit of measure errors.
The main advantage of data correction through such scripts is that it allows for a quick way to translate knowledge to (well-documented) code. Possible disadvantages include lack of reproducibility when code is not under a decent version control system or when manipulations are done by hand. Also, each statement solves a single problem, not taking into account other such statements or validation rules. Indeed, it is our experience that in some cases these scripts do more damage to a data set, in terms of the number of violated validation rules, than they do good. One would therefore like to keep track of such modifications, and at least have some knowledge about whether they interfere with each other or not.
One solution is to define simple knowledge rules not hard-coded in the processing software but to provide them as parameters to a program that applies the rules to data and monitors their effects. This way, the impact of each rule can be kept track of and evaluated. The implementation of such an approach is necessarily a trade-off between flexibility and maintainability. In the most flexible case, a user can insert arbitrary code to alter the data and the system only keeps track of the changes. This means that maintaining such a rule set is as complex as maintaining any software system. In particular, it will be very difficult to discover contradictions or redundancies in such code, and one needs to resort to software testing techniques to guarantee any level of quality. On the more restricted side, one can restrict the type of rules that may be specified, allowing for some (automated) ways of interpreting their properties before confronting them with the data.
Two interesting properties of such rules present themselves. First, note that the condition in rules of the type (9.1) detects an invalid situation. The first requirement we have on a modifying rule is therefore that it actually solves that particular invalidity. In other words, if we apply the same rule twice to a data set, no modification is done at the second round. Second, it would be nice if the rules do not interfere with each other. That is, if one such knowledge rule is applied, we do not wish it to modify the data in such a way that a second rule is necessary to repair the damage done. In general, we shall demand that the order of execution of such rules is not important. Both properties together greatly enhance maintainability and understandability of the rule sets.
In the following section, we will give a formal definition of modifying rules in terms of ‘modifying functions’. This allows us to make the two demands on modifying functions more precise and to study the conditions under which they hold. We shall see that we can obtain necessary and sufficient condition for the first demand and only a sufficient condition for the second. After discussing these general conditions, they will be made explicit for an important class of rules on numerical data. In Section 9.2, we will show how modifying rules can be applied to data from R. Readers who are less interested in the theoretical aspects can skip Section 9.1 on first reading.
9.1.1 Modifying Functions
In the following discussion, it will be assumed that the data to be treated is a rectangular data set consisting of 
records and 
variables, which are not necessarily stored in the correct type. The measurement domain of each variable is denoted 
, so a record of 
variables is an element of 
(this is a special case of the definition of the measurement domain in Section 6.3.1).
We interpret a modifying rule as a function 
. Both the input and the output are in the measurement domain, since we do not demand that a single modifying rule fixes every issue a record might have (although it is also not excluded). We will use the term modifying function (to be made precise at the end of this section) to indicate a function based on a data modifying rule.
Before giving the formal definitions, let us look at an example. Consider the following rule:
For compactness we will use the shorthands 
for general expenditures, 
for total expenditures, and 
for other expenditures. The measurement domains for each variable is given by 
, so we have 
. A formal expression of the rule in terms of a function is simply the following:
Here, the notation 
indicates the open range 
. We also include explicitly the demand 
since we do not want to (re)set a value unnecessarily.
The form of function (9.3) is easy to generalize in the following formal definition.
This definition includes the case where 
, meaning that 
is transformed to 
in any case. If 
is a proper subset of 
(
), then we can interpret 
as an invalid region, and the rule is an attempt to move a record 
out of this invalid region.
Idempotency
Consider again the modifying function of Eq. (9.3). It is easy to see that if we replace a record 
with 
a second application of 
will not change the result. To see this, we need to check two cases: the cases where the initial record satisfies the condition and the cases where the condition is not satisfied. Starting with the latter case, suppose that for our original record we have 
. In that case, we have 
and therefore 
. Now, if we have 
for the original record, we get 
. Since we now have 
, the result of 
.
The point is that once a record is moved out of an invalid region, we do not want the function to move it again. The property that iterating a function twice does not alter the result is referred to as the idempotent property of a function, which we will now define formally.
The idempotent property is not only desirable from the theoretical or subject-matter points of view. The main practical benefit is that the function, or its underlying rule, can be interpreted just by understanding the definition of the condition and the function 
without regarding possible iterations of the rule. It is therefore useful to have some general conditions under which a modifying function is idempotent. Intuitively, a modifying function should be idempotent when 
takes a record 
out of the invalid region, as depicted in Figure 9.1. The following proposition claims that this is indeed a necessary and sufficient condition.
To show that 
is indeed idempotent on whole 
under these conditions we prove it separately for the complement of 
in 
(denoted 
) and for 
.
It is not difficult to define modifying functions that are not idempotent. Exercise 9.1.2 is aimed to give an example of how such situations may occur.
Figure 9.1 Idempotency of a modifying function. The full rectangle represents the measurement domain 
. The portion in the rectangle outside of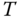 
is valid according to the condition in 
. The region 
is considered invalid. The function 
maps an invalid record to a valid one and a valid record to itself.
Commutativity
Consider an example rule that can be used to detect and repair unit-of-measure errors where units are off by a factor of 1000. We use the same variables as in Eq. (9.3).
The formal definition can be written as follows:
The result of applying both 
and 
to a record 
may well be order-dependent. Consider a record for which 
. Then for sure it must be in 
. Now, if we apply first 
and then 
we get 
. If 
then 
. Now, suppose we first execute 
and then 
. We have 
.
So here we have a case where the order of execution of a set of modifying functions 
may be important for the result. For larger sets of modifying rules, such interdependencies make the action of any single rule on a data set hard to judge. In the worst case, one function may undo the action of another. When designing a set of rules, it is therefore desirable to detect these cases so the ‘risk of collision’ can be assessed or to avoided altogether.
The technical term for independence of order of execution is called commutativity of two functions, which are now ready to define precisely.
Two functions trivially commute when they act on different variables. If two modifying functions 
and 
act on different variables in the condition as well as in the consequent, the action of the first function cannot alter the outcome of the second. Apart from acting on different variables, we can derive some very general sufficient (but not necessary) conditions under which two modifying functions commute. These are stated in the following proposition.
Before stating the proof, it is elucidating to consider the situation depicted in Figure 9.2. Here, 
and 
are modifying functions that we define to be idempotent on all of 
. On the right, we see that 
and 
commute on the point 
: the dashed lines correspond to 
and the solid arrows correspond to 
. On the left, we see that 
and 
do not commute on the point 
, because 
takes 
into the invalid region of 
(labeled 
), after which 
takes 
out of 
. Again, following the solid arrows corresponds to 
and following the dashed lines corresponds to 
.
The proof of the proposition now consists of carefully considering the four regions in the diagram: 
less the valid regions, region 
less 
, region 
less 
, and the intersection of 
and 
.
Figure 9.2 Commutativity of idempotent modifying functions. The full rectangle including subsets 
and 
corresponds to the measurement domain 
. The idempotent modifying functions 
and 
commute on 
but not on 
.
The above outline of a procedure combines the trivial notion that two functions commute when they act on different variables with the general conditions derived above. This procedure does not guarantee that mutually interfering rules can always be found automatically. It does provide a strategy that can be partially automated to indicate possible conflicts. In order to be able to explicitly test the conditions for idempotency or commutativity given in Propositions 9.1.3 and 9.1.5, we need to assume more about the type of rules. In the following section, these conditions are made explicit for an important class of direct rules.
9.1.2 A Class of Modifying Functions on Numerical Data
Many modification rules on numerical data that are used in practice can be written in the form
Here, the real matrices 
and 
are of dimensions 
and 
, respectively, and we assume that the system 
is feasible. A transformation that sends a vector 
to 
is called an affine map. Hence, we will call a modifying function as in Eq. (9.6) an affine modifier with linear inequality conditions, or AMLIC for short.
It was noted by Scholtus (2015) that affine maps cover several common operations that are performed either manually by analysts or via automated processing of modifying rules. In particular, we will show that such mappings can be used to replace values by a constant, multiply values by a constant, swap values in a record, and compute a value from a linear combination of other values in the record.
As an example, we will study three variables: turnover, other revenue, and total revenue. A record containing a value for each of these variables can be represented as a vector 
, where 
is the value of turnover, 
the value of other revenue, and 
the value of total revenue.
There are other examples, which will be discussed in Exercise 9.1.5.
Given that several such common operations can be expressed in the form of Eq. (9.6), it is interesting to see if general and explicit conditions of idempotency and commutativity can be derived. As we will be shown next, this is indeed the case.
Idempotency
According to Proposition 9.1.3, we need to check if every vector 
in 
is mapped to a vector that satisfies the opposite. That is, we need to ensure that any vector 
(
) does not satisfy 
, that is, we demand that
for all 
satisfying 
. These demands are summarized by stating that the system
has no solutions. The consistency of such systems can be determined, for example, through Fourier–Motzkin elimination.
Commutativity
Given two modifying functions 
and 
of the class defined by Eq. (9.6). Also define 
and 
to be their respective invalid regions, defined by 
and 
. The modifying function of 
is defined by 
and the modifying function of 
is defined by 
. Before stating Procedure 9.1.1 explicitly for this case, we derive sufficient conditions for the two functions to be commutative, in the case that they are idempotent.
If 
and 
are idempotent, we need to check the three conditions of Proposition 9.1.5. Conditions 1 and 2 are related to regions 
and 
, respectively, and they state that any vector in those regions must be mapped outside of 
. Using a similar reasoning as for Eq. (9.7), we arrive at the conclusion that this is equivalent to stating that the systems of inequalities given by
have empty solution spaces.
The third condition states that for any vector in 
, the modifying functions must be equal so 
for all 
. Let us denote with 
the region where this equality holds, so 
. The condition implies that every 
is also in 
, or 
. To express this in terms of systems of linear equations, we can restate this by demanding that 
. Now, 
is a set of vectors that is defined by not satisfying a set of linear equalities. A vector is a member of this set when it violates at least one of those restrictions. Now, let us denote with 
the 
th row of the matrix 
. The 
th restriction defining 
is given by
For a vector to violate this restriction, it should satisfy either
or
We are now able to state the third condition in terms of demands on sets of linear restrictions. The set 
is empty if for at least one of the 
one of the two sets
is infeasible.
Now that we have derived explicit conditions for the commutativity of two modifiers we can specialize Procedure 9.1.1 to affine modifiers with linear inequality constraints. The above procedure is stated in a fairly general way, and may in principle involve many feasibility checks on systems of linear inequations. In practice, user-defined rules commonly involve only one or a few linear inequality conditions and only very simple transformations that involve few variables. So in many cases this procedure will be computationally tractable.
Exercises for Section 9.1
9.2 Rule-Based Correction with dcmodify
The package dcmodify implements a work flow where data modifying rules are not part of data processing software, but instead are stored and manipulated as parameters to a data cleaning workflow. The situation is depicted schematically as follows:
Here, a set of rules defines how data is modified. The allowed rules are assignments that executed possibly within a (nested) conditional statement. Just like the validate package, dcmodify employs a subset of the R language for rule definition.
The simplest command-line use is implemented as the modify_so function, accepting a data.frame and one or more (conditional) modifying rules.
library(dcmodify)
dat <- data.frame(x = c(5,17), y = c("a","b"),stringsAsFactors=FALSE)
modify_so(dat, if( x > 6 ) y <- "c")
## x y
## 1 5 a
## 2 17 cThe function is set up so it can be integrated in a stream-like syntax facilitated by the magrittr package.
library(magrittr)
dat %>% modify_so(
if (x > 6) y <- "c"
, if (y == "c") x <- 11 )
## x y
## 1 5 a
## 2 11 cWe point out two observations. First, the conditional statements are interpreted as if they are executed record by record. Under the hood, optimization takes place to make sure that code is executed in vectorized manner. Second, the rules are executed sequentially. In the example, the first rule changes the value of y from "b" to "c". Next, the second rule changes the value of x from 6 to 11 in the second record because the value of y is now "c". (Needless to say, these two rules do not commute in the sense explained in the previous section). This is in fact default behavior that can be toggled by setting the sequential option to TRUE.
9.2.1 Reading Rules from File
The dcmodify package follows the structure of the validate package. Like in validate, there is an object storing rules, the difference being that rules are stored in an object called modifier and not validator, reflecting the purpose of the rules. To execute the rules, there is a function called modify that ‘confronts’ a data set with a set of modifying rules.
mod <- modifier(
if ( x > 6 ) y <- "c"
, if ( y == "c" ) x <- 11
)
modify(dat, mod)
## x y
## 1 5 a
## 2 11 cModifying rules may be read from and stored to files just like validation rules, and the structure of the files is the same as discussed in Section 6.5.6, except that the rule syntax is different. So rule may be defined in a free-format text file such as the following:
# modifiers.txt
if ( x > 6 ){
y <- "c"
}
if ( y == "c" ){
x <- 11
}Subsequently, rules may be read with modifier using the .file argument.
mod <- modifier(.file="modifiers.txt")Moreover, modifier objects support the same metadata as validator objects, so functions such as origin, label, and variables also work on modifier objects.
variables(mod)
## [1] "x" "y"Metadata can be defined using the yaml format described earlier in Section 6.5.6 as well. So, for example, the following file defines a bit of metadata for one of the rules defined earlier:
rule:
-
expr: |
if ( x > 6 ) y <- "c"
name: fix_x
description |
When `x' is too large, the y-category must be 'c'.9.2.2 Modifying Rule Syntax
The general structure of a modifying statement allowed currently by the dcmodify package follows the following very simple syntax diagram:
Curly braces (blocks) have been left out for clarity. In short, a modifying statement consists of one or more assignments, possibly executed under a (nested) conditional statement.
The following examples illustrate the type of rules that can be defined with this syntax:
# multiple assignment
if ( x> 0 ){
x <- 0
y <- 2 * y
}
# nested conditions
if ( x> 0 ){
x <- 0
if ( y < 10 ){
y <- 2*y
}
}
# reassignment
x <- y - 7Like in the validate package, it is possible to define variable macros (using the := operator) or variable groups (with vargroup). In other words, the modifier defined by
modifier(
x_limit := 10*median(x)
, if ( x > x_limit) x <- NA
)is equivalent to
modifier( if ( x > 10*median(x) ) x <- NA )9.2.3 Missing Values
It may occur that the condition in a modifying rule cannot be evaluated because one or more of the necessary values are missing. By default, the package then assumes that the result is FALSE. For example, compare the output for the two-record data set in the following code:
dat <- data.frame(x=c(NA, 0), y=c(0,0))
m <- modifier( if ( x == 0 ) y <- 1 )
modify(dat, m)
## x y
## 1 NA 0
## 2 0 1In the first record, the condition x == 0 could not be evaluated so the result FALSE was assumed and consequently, y is left untouched. The second record could be evaluated normally.
The default assumption that an NA in the condition is interpreted as FALSE can be altered with the option na.condition.
modify(dat, m, na.condition=TRUE)
## x y
## 1 NA 1
## 2 0 19.2.4 Sequential and Sequence-Independent Execution
In principle, execution of one rule can influence the condition of another rule (see also the discussion of Section 9.1.1). As an example, consider the following single-row data set and sequence of modifications:
dat <- data.frame(x = 0, y = 0)
m <- modifier(
if ( x == 0 ) x <- 1
, if ( x == 0 ) y <- 1
)If we apply the modifier to the data, the first modifying rule will set x to 1, since x equals zero. The consequent of the second rule is not executed since now x has changed.
It may occur that the decision to execute the second statement should not depend on previously executed rules. This can be controlled by setting the option sequential=FALSE. As an example, consider the following outputs:
modify(dat, m)
## x y
## 1 1 0
modify(dat, m, sequential=FALSE)
## x y
## 1 1 1In the second case, the conditional part of a rule is always evaluated using the original data. So in the second case, the condition x == 0 always evaluated to TRUE, regardless of the changes made by the first rule.
9.2.5 Options Settings Management
The option settings for the dcmodify package are handled by the same options manager as for the validate package. This means (again) that options can be set on a global level using validate::voptions.
voptions(na.condition=TRUE)It is also possible to attach options to objects carrying rules, including modifier objects.
voptions(m, sequential=FALSE)The options hierarchy, where global options (set with voptions) are overruled by options attached to an object, which are again overruled by options passed during a function call are the same as for the validate package as well.
9.3 Deductive Correction
In some cases, inconsistencies in a data record can be traced back to a single origin, either by (automatic) reasoning based on the validation rules or by allowing for a weak assumption based on subject matter knowledge. In general, deductive correction methods allow one to use data available within a faulty record to find a unique correction that fixes one or more inconsistencies.
For example, suppose we have a numerical record with integer values 
, subject to the rule 
(
rofit plus 
ost equals 
urnover). Without any further information, Fellegi and Holt's principle tells us that one randomly chosen variable should be altered. However, if we study the values a little, we see that the record can be made consistent with the rule if we swap the last two digits in the value for turnover: 
, assuming that a typo has been made.
Over the years, several algorithms have been developed and implemented that allow various forms of deductive data correction. Such algorithms are often specific to a certain data type, a certain type of validation rules, and certain assumptions about the cause of error. In the following section, we highlight a number of those algorithms and show how they can be applied in R.
9.3.1 Correcting Typing Errors in Numeric Data
Integer data that is entered by humans may contain typing errors that cause violations of linear equality restrictions. If such errors can be detected, they may be repaired by replacing the erroneous value with a valid one. Scholtus (2009) describes a method for detecting and repairing typing errors in numerical data under linear restrictions. The basic idea is both elegant and simple; given a record violating one or more restrictions, one generates a number of candidate solutions by keeping one or more variables fixed and solving for the other ones using the linear restrictions. If the values in the candidate solution are not more than, say, a single typing error away from the original value, it is assumed that a typing error has been made. Finally, from all the candidate solutions, a trade-off between the minimal number of changes with the maximum number of resolved violations determines what changes are actually applied.
Area of Application
This method can be applied to records containing integer data, subject to at least set of linear equality restrictions that can be written as
where 
, and 
have integer coefficients. Such a subset is necessary to generate candidate solutions. There may be more (in)equality restrictions, but these are only used to check that proposed solutions do not generate extra violations. The demand that 
contains only integer values poses a restriction on the constraint matrix. In particular, 
must be a totally unimodular matrix for Eq. (9.10) to have any integer solutions. A matrix is totally unimodular when every nonsingular square submatrix has determinant 
, which again implies that each coefficient 
. There are several tests for unimodularity available, such as those described by Heller and Tompkins (1956) or Raghavachari (1976), and the lintools R package implements a combination of them.
Although a general classification of unimodular matrices seems to be missing, the authors have never encountered a practical set of restrictions that did not satisfy the unimodularity criterion. The reason is that many restriction sets are balance restrictions of the form 
that follow a tree-like structure. In such systems, there is a single overall result, for example, total profit 
total revenue 
total cost, and each term on the right-hand side is the sum of new subvariables (a list of particular costs, a list of particular revenues, and so on). Each subvariable can be the sum of new variables again. It is not hard to see that for this important class of tree-like balance structures, an integer solution can always be constructed by choosing an integer for the top result variable, and recursively choosing values down the tree, so in these cases the corresponding restriction matrix must be totally unimodular.
The Algorithm
In his original work, Scholtus identifies typographical errors by studying their effect on the decimal expansion of integers. Here, we generalize the method a little by treating an integer as a string and allowing for any typographical error based on an edit-based string metric as described in Section 5.4.1. This has the advantage that sign errors can be detected and repaired as well. Moreover, in the original formulation, the set of equality restrictions was limited to the form 
, whereas we treat the case of Eq. (9.10). The approach described as follows was first described in van der Loo et al. (2011).
The algorithm consists of two main parts. First, a list of candidate solutions is generated. Next, a subset of candidates that is in some sense optimal is selected from the set of candidates. The following procedure gives an overview of the algorithm.
Here, in step 
attention is restricted to variables that occur only in violated restrictions since altering a variable that also occurs in a satisfied equality restriction would lead to new violations. To explain the second step, first note that given a violated restriction of the form 
, one can always find a solution that resolves the violation choosing a variable and solving it from the restriction. In step 
, this is done for each variable occurring in each violated restriction. Each such solution is considered a candidate if it differs no more than a certain string distance from the original value. The set of candidates 
may therefore in general contain multiple suggestions for each variable. In step 
, the set of candidate solutions is reduced by selecting the subset of candidates that (1) contains only one suggestion for each chosen variable, (2) maximizes the set of satisfied restrictions, and (3) does not violate any extra restrictions that were not violated before. This maximization be performed by generating all subsets without duplicate suggestions and computing the violations after substituting the suggestions in the original record 
.
There are some extensions of this algorithm that make it more useful in practice. The first extension is to allow for linear (in)equations. The subset selection method in the final step can take these into account by checking that the chosen solution does not violate any new inequality restrictions. The second extension allows for missing values by eliminating missing values from the set of (in)equations before running the algorithm just described.
Correcting Typographical Errors in Numerical Data with R
The package deductive implements the algorithm for correcting typographical errors described above. The restrictions may be defined using the validate package. Example 9.3.10 can be computed in R as follows:
library(validate)
library(deductive)
dat <- data.frame(x1 = 123, x2 = 192, x3 = 252)
v <- validate::validator(x1 + x2 == x3)
deductive::correct_typos(dat, v)
## x1 x2 x3
## 1 123 129 252The correct_typos function accepts a data set and a rule set and returns a data set with corrections where possible. By default the maximum accepted edit distance (measured as optimal string alignment, see Section 5.4.1) equals one. The distance measure may be set by passing method="[methodId]" where [methodId] is any method accepted by stringdist::stringdist (see Section 5.4.2).
Here is an example with a sign error, which may be detected as a typographical error.
dat <- data.frame(x1 = -123, x2 = 129, x3 = 252)
deductive::correct_typos(dat,v)
## x1 x2 x3
## 1 123 129 252The deductive package extends Procedure 9.3.1 by also rejecting solutions that would cause new violations of restrictions that are not used in deriving candidate solutions.
dat <- data.frame(x1 = -123, x2 = 129, x3 = 252)
v <- validate::validator(x1 + x2 == x3, x1 < 0)
deductive::correct_typos(dat, v)
## x1 x2 x3
## 1 -123 129 252Here, no correction is applied to x1 since switching it from negative to positive would break the rule x1 < 0.
Exercises for Section 9.3.1
9.3.2 Deductive Imputation Using Linear Restrictions
Correction of numerical records that are subject to a set of linear (in)equations is often a multistep process during which existing values are accepted as correct, missing values imputed or erroneous values removed. Once all erroneous values are removed, a record can be thought of as consisting of two parts: a part with correct values and a part missing. Since the now-present values are deemed correct, they may be substituted in the system of restrictions, yielding a reduced system that applies to the unobserved values. If sufficient values have been substituted, the reduced set of restrictions may restrict one or more unobserved values to a unique value.
One way of flushing out such implied equalities for a variable, say 
, is by eliminating one by one all other variables until either no restriction pertaining to 
is left, or an obvious unique value for 
occurs. Repeating this procedure for each missing value yields every value that is uniquely implied by the reduced system of restrictions. For systems with inequalities, the elimination procedure involves Fourier–Motzkin elimination that quickly becomes intractable as the number of variables grows; the number of implied inequations maximally grows exponentially with the number of eliminated variables.
As an alternative, one may attempt to derive as many implied values as possible using other, more heuristic methods. These methods do not necessarily find every unique imputation, but they have significantly lower complexity than Fourier–Motzkin-based methods. Once the heuristic methods have been applied, a (possibly) smaller set of missing values remain, leaving a simpler problem for the elimination-based methods.
Below, we describe three such methods. The first one is based on computing the Moore–Penrose pseudoinverse for the subset of equality restrictions, the second finds zero imputations in specific cases and the recursively third finds combined inequations that imply a simple equality.
Extracting Implied Values from the Subsystem of Equalities
For this method, we assume we have a numerical record 
for which a number of values are missing. The values may have been missing from to begin with or perhaps have been removed after application of a suitable error localization method. We furthermore suppose that 
must satisfy a set of linear restrictions denoted
It is possible that the record is subject to inequality restrictions as well, but these may be ignored here.
Sorting the values conveniently, we may write 
, where 
stands for observed and 
for missing. Likewise, the columns of the restriction matrix 
can be sorted so that we can write
This may be rewritten to obtain a set of demands on the missing values, expressed in the observed values.
Note that the right-hand side of this equation is fully known since it is computed from the observed values.
We are now left with three cases. The first option is that the system 
has no solutions. In that case, either the system of Eq. (9.11) was inconsistent to begin with, or the values of 
are such that the system 
is rendered inconsistent. Note that this is never the case when the original system was consistent and an appropriate error localization algorithm was applied. The second option is that 
is square and of full rank so it can be inverted. In that case, we can impute the missing values uniquely by setting 
. The third option is that there are an infinite number of solutions. It can be shown that every solution 
can be expressed as
where 
is the so-called Moore–Penrose pseudoinverse of 
and 
is any vector in 
with 
the number of missings. We refer the reader to the appendix of this section for a short discussion of the Moore–Penrose matrix and the notation for this solution.
We may use Eq. (9.13) for deductive imputation in the following way. Suppose that the 
th row of the matrix 
is filled with zeros. Since the Moore–Penrose pseudoinverse is unique, the 
th coefficient of 
is then uniquely determined by the 
th element of the first term in Eq. (9.13).
Using Nonnegativity Constraints
Under some specific circumstances, nonnegativity constraints combined with a linear equality restriction can lead to unique solutions. For example, suppose we have the following balance rule:
where all 
. Now if 
, 
, and 
are observed with values such that 
, and 
and 
are missing, the unique possible values for 
and 
equals zero (assuming that the observed values are indeed correct). Such cases occur for instance, where only nonzero values have been submitted to a survey or administrative system.
To generalize this to a general linear equality restriction, we write
We may replace 
with 
if the following conditions are fulfilled (de Waal et al., 2011):
.
is restricted by 
.- All coefficients of
have the same sign.
Deducing Values from Combined Inequalities
Given a record 
subject to a set of rules 
. Substituting the observed values 
in the set of inequations, we obtain a reduced system
If the reduced system contains one or more pairs of inequations of the form
where
then 
may be substituted by 
. Since this method of imputation depends on substituting known values, the procedure is iterated by substituting imputed values into the system of inequations (9.17), detecting new pairs and imputing those until no new pairs are found.
Combining Methods
The three methods described above are not completely independent. For example, it is possible that after a record is partially imputed using Eq. (9.14), more zeros can be deductively imputed based on the nonnegativity constraints. These methods should therefore be applied in chain and iteratively until no further imputations can be found.
Deductive Imputation in R
The methods for deductive imputation mentioned above have been implemented in the deductive package. The function impute_lr (lr for linear restrictions) iteratively applies the heuristic methods, before computing the variable ranges of missing values by Fourier–Motzkin elimination. Here, we demonstrate Example 9.3.11.
library(validate)
library(deductive)
v <- validate::validator(
x1 + x2 == x3
, x4 + x5 + x6 == x1
, x7 + x8 == x2
, x9 + x10 == x3)
dat <- data.frame(
x1 = 100, x2=NA_real_, x3=NA_real_, x4 = 15, x5 = NA_real_
, x6 = NA_real_, x7 = 25, x8 = 35, x9 = NA_real_, x10 = 5)
dat
## x1 x2 x3 x4 x5 x6 x7 x8 x9 x10
## 1 100 NA NA 15 NA NA 25 35 NA 5
impute_lr(dat,v)
## x1 x2 x3 x4 x5 x6 x7 x8 x9 x10
## 1 100 60 160 15 NA NA 25 35 155 5The function impute_lr accepts a data set and a number of rules in the form of a validator object. The result is a data set where fields that have a unique solution are imputed.
The following exercise shows how to apply impute_lr to a larger data set and how to interpret the results.
Exercises for Section 9.3.2
Appendix 9.A: Discussion of Equation (9.13)
Using some properties of the pseudoinverse, we will show that Eq. (9.13) is indeed a solution to the system of Eq. (9.12). Theory of the Moore–Penrose inverse is available in many textbooks, such as the book by Lipshutz and Lipson (2009) (where it is called the generalized inverse). The paper by Greville (1959) is a good early reference that discusses applications to linear systems and statistics.
The Moore–Penrose Pseudoinverse
The Moore–Penrose pseudoinverse (or just: pseudoinverse) is a generalization of the standard inverse of a square invertible matrix. Suppose that 
is an invertible square matrix with singular value decomposition 
, then its inverse is given by 
where 
is the matrix with the reciprocal eigenvalues of 
on the diagonal. If 
is not of full rank (this includes the case where it is not square), we can still decompose it using a singular value decomposition but since one or more eigenvalues are zero, 
is not defined. To compute the Moore–Penrose pseudoinverse, 
is replaced by 
, which is the matrix that has zero at the diagonal when the singular values are zero and the reciprocal singular value otherwise. We note that it is not necessary to use the svd theorem to define the Moore–Penrose pseudoinverse, but the explicit construction does make it easier to understand the generalization and some of its properties.
In particular, it is easy to demonstrate by svd decomposition that the pseudoinverse of a matrix 
has the property
This equation also shows that the matrix 
is a left identity of 
. That is, it has the property that 
. Using associativity of matrix multiplication and Eq. (9.18), one sees that 
is idempotent: 
.
9.A.2 Equation (9.13) is a Solution
First recall that if 
is a solution to 
, than for any vector 
for which 
, the vector 
is also a solution (we say that 
). Using Eq. (9.18), we see that the second term in Eq. (9.13) is in 
:
So to show that Eq. (9.13) is a solution to the system of Eq. (9.12), we only need to show that the term
satisfies 
(we introduce 
as a convenient shorthand for 
). This can be done with the following calculation:
Here, we used that 
spans a basis for the column space of 
.