Appendix A
Matrix Forms and Relationships
The following matrix forms, properties, and relationships are useful in the derivation of state estimators [18,52]. Vectors are depicted with small letters as a, x, … and matrices with capital letters as X, Y, … The matrix forms and relationships are united in groups depending on properties and applications.
A.1 Derivatives
The following derivatives of matrix and vectors products and traces of the products allow deriving state estimators in a shorter way.
A.2 Matrix Identities
There are several matrix identities that are useful in the representation of the inverse of the sum of matrices.
The Woodbury identities [59]:
For positive definite matrices 
and 
, there is
The Kailath variant:
Special cases:
A.3 Special Matrices
The Vandermonde matrix: This is an 
matrix with the terms of a geometrical progression in each row,
The Jacobian matrix: For 
and 
,
The Hessian matrix: For 
and 
,
Schur complement:
Given 
, 
, 
, 
, and a nonsingular block matrix
If 
is nonsingular, then the Schur complement of 
is 
, and the inverse of 
is computed as
If 
is nonsingular, then the Schur complement of 
is 
, and the inverse of 
can be computed by
A.4 Equations and Inequalities
Several equations and inequalities are used to guarantee the stability of state estimators.
The Riccati differential equation (RDE):
A solution to (A.12) can be found if we assign
and choose matrices 
and 
such that
Next, the derivative 
can be transformed as
that gives an equation
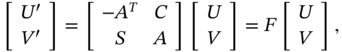
for which the solution
The continuous‐time algebraic Riccati equation (CARE):
where 
is the unknown symmetric matrix and 
, 
, 
, and 
are known real matrices.
The discrete‐time algebraic Riccati equation (DARE):
where 
is the unknown symmetric matrix and 
, 
, 
, and 
are known real matrices.
The discrete dynamic (difference) Riccati equation (DDRE):
where 
is a symmetric positive semi‐definite matrix and 
is a symmetric positive definite matrix.
The discrete‐time algebraic Riccati inequality (DARI):
where 
is the unknown symmetric matrix and 
, 
, 
, and 
are known real matrices; 
, 
, and 
.
The nonsymmetric algebraic Riccati equation (NARE):
where 
is the unknown nonsymmetric matrix and 
, 
, and 
are known matrices; 
, 
, and 
. The NARE is a quadratic matrix equation.
The continuous Lyapunov equation:
where 
is a Hermitian matrix and 
is the conjugate transpose of 
. The solution to (A.31) is given by
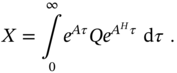
The discrete Lyapunov equation:
where 
is a Hermitian matrix and 
is the conjugate transpose of 
. The solution to (A.33) is given by an infinite sum as
A.5 Linear Matrix Inequalities
The LMI has the form of [22]
where matrix 
is positive definite, 
is the variable, and the symmetric matrices 
, 
, are known. The following fundamental properties of the LMI (A.36) are recognized:
- It is equivalent to a set of
polynomial inequalities in 
; i.e., the leading principal minors of 
must be positive. - It is a convex constraint on
; i.e., the set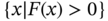 
is convex.
The LMI (A.36) can represent a wide variety of convex constraints on 
. In particular, this includes linear inequalities, (convex) quadratic inequalities, and matrix norm inequalities. The Riccati and Lyapunov matrix inequalities can also be cast in the form of an LMI.
When the matrices 
are diagonal, the LMI 
is a set of linear inequalities. Nonlinear (convex) inequalities are converted to LMI form using Schur complements (A.22)–(A.24). The basic idea associated with the matrix (A.22) is as follows: the LMI
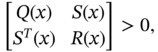
where 
, 
, and 
depend affinely on 
, is equivalent to
It then follows that the set of nonlinear inequalities (A.38) can be represented as the LMI (A.36).
If the Riccati, Lyapunov, and similar equations are written as inequalities, then they can readily be represented as the LMI.
A numerical solution to the LMI considered as the convex optimization problem can be found using the interior‐point methods.