C.5. Numerical Determination of Optimal Trajectories

Search in book...
Toggle Font Controls
Create new playlist

Name your new playlist

Playlist description (optional)
Sign In

Email address

Password

Forgot Password?

or

Continue with Facebook

Continue with Google
Sign Up

Full Name

Email address

Confirm Email Address

Password

or

Continue with Facebook

Continue with Google

C.5. Numerical Determination of Optimal Trajectories

In the previously presented approach (variational approach to optimal control problems), the problems usually emerge as nonlinear, two-point boundary-value problems, which also typically cannot be solved analytically to obtain an optimal control law, or an optimal open-loop control. In this case, iterative numerical techniques may be used to determine open-loop optimal controls. In this subsection, we briefly present some candidate numerical approaches that can be used in order to compute optimal control laws, or optimal open-loop controls whenever this is not analytically possible. We present the general concepts of these numerical approaches and point toward suitable references for detailed presentations for the more interested reader.

The general problem addressed is given by the following system of equations:

$\begin{matrix} {\dot{x}}^{*} (t) = \frac{\partial H}{\partial p} = a (x^{*} (t), u^{*} (t), t), \\ {\dot{p}}^{*} (t) = - \frac{\partial H}{\partial x} = - {[\frac{\partial a}{\partial x} (x^{*} (t), u^{*} (t), t)]}^{T} p^{*} (t) - \frac{\partial g}{\partial x} (x^{*} (t), u^{*} (t), t), \\ 0 = \frac{\partial H}{\partial u} = {[\frac{\partial a}{\partial u} (x^{*} (t), u^{*} (t), t)]}^{T} p^{*} (t) + \frac{\partial g}{\partial u} (x^{*} (t), u^{*} (t), t), \\ x (t_{0}) = x_{0}, \\ p^{*} (t_{f}) = \frac{\partial h}{\partial x} (x^{*} (t_{f})) . \end{matrix}$

(C.47)

It considers unbounded states/controls with

$t_{f}$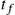

$x (t_{f})$

free. From the system of state/costate equations and boundary conditions, it is possible to obtain an explicit relationship between

$x^{*} (t)$

and

$u^{*} (t)$

$t \in [t_{0}, t_{f}]$

dependent on

$x_{0}$

. Assuming

$u^{*} (t) = f (x^{*} (t), p^{*} (t), t)$

and substituted in the state/costate equations, a set of

$2 n$

first-order ODEs (actually reduced ODEs can be obtained and considered with the boundary conditions

$x (t_{0}) = x_{0}$

and

$p^{*} (t_{f}) = \frac{\partial h}{\partial x} (x^{*} (t_{f}))$

. If the boundary conditions are all known at

$t_{0}$

$t_{f}$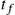

, then the optimal control law

$x^{*} (t), p^{*} (t), t \in [t_{0}, t_{f}]$

can be obtained by numerical integration and the optimal control history can be found by substitution in the previous relation.

The basic strategy in all of following three numerical approaches considered (steepest descent, variation of extremals, and quasilinearization) is to initially guess a solution so that one of the three set of equations (state/costate/Hamiltonian) is not satisfied. Then a solution is used to adjust the initial guess, i.e. make the next solution closer to satisfying all necessary conditions. Finally, the steps are repeated until the iterative procedure converges.

When the boundary values are split⁵ (for nonlinear equations), the above cannot be applied and the gradient projection is a more suitable approach.

C.5.1. Steepest Descent

For a function of multiple variables to have a relative minimum at a point, it is necessary that the gradient of the function is zero at this point, which in general yields a system of nonlinear differential equations. Suppose

$u^{(i)} (t), t \in [t_{0}, t_{f}]$

is known and used to solve

${\dot{x}}^{(i)} (t) = a (x^{(i)} (t), u^{(i)} (t), t), x^{(i)} (t_{0}) = x_{0},$

(C.48)

${\dot{p}}^{(i)} (t) = - \frac{\partial H}{\partial x} (x^{(i)} (t), u^{(i)} (t), p^{(i)} (t), t), p^{(i)} (t_{f}) = \frac{\partial h}{\partial x} (x^{(i)} (t_{f})) .$

(C.49)

$u^{(i)} (t)$

satisfies

$\frac{\partial h}{\partial x} (x^{(i)} (t_{f})) = 0$

, for

$t \in [t_{0}, t_{f}]$

as well, then

$x^{(i)} (t), u^{(i)} (t), p^{(i)} (t)$

are extremal.

If the above are not satisfied, then

$δ J_{a} = {[\frac{\partial h}{\partial x} (x^{(i)} (t_{f})) - p^{(i)} (t_{f})]}^{T} δ x (t_{f}) + \int_{t_{0}}^{t_{f}} {{[{\dot{p}}^{(i)} (t) + \frac{\partial H}{\partial x} (x^{(i)} (t)), u^{(i)} (t) p^{(i)} (t), t)]}^{T} δ x (t) + {[\frac{\partial H}{\partial u} (x^{(i)} (t)), u^{(i)} (t) p^{(i)} (t), t)]}^{T} δ u (t) + {[a (x^{(i)} (t), u^{(i)} (t), t) - {\dot{x}}^{(i)} (t)]}^{T} δ p (t)} d t,$

where

$δ x (t) = x^{(i + 1)} (t) - x^{(i)} (t)$

$δ u (t) = u^{(i + 1)} (t) - u^{(i)} (t)$

and

$δ p (t) = p^{(i + 1)} (t) - p^{(i)} (t)$

If the necessary conditions are satisfied however, then

$δ J_{a} = \int_{t_{0}}^{t_{f}} {[\frac{\partial H}{\partial u} (x^{(i)} (t)), u^{(i)} (t) p^{(i)} (t), t)]}^{T} δ u (t) d t .$

If the norm of

$δ u$

$‖ u^{(i + 1)} - u^{(i)} ‖$

is small, the sign of

$Δ J_{a} = J_{a} (u^{(i + 1)}) - J_{a} (u^{(i)})$

will be determined by the sign of

$δ J_{a}$

. Then, if

$δ u (t) = u^{(i + 1)} - u^{(i)} = - τ \frac{\partial H^{(i)}}{\partial u} (t), t \in [t_{0}, t_{f}]$

with

$τ > 0$

$δ J_{a} = - τ \int_{t_{0}}^{t_{f}} {[\frac{\partial H^{(i)}}{\partial u} (t)]}^{T} [\frac{\partial H^{(i)}}{\partial u} (t)] d t \leq 0,$

and in this case the equality holds if and only if

$\frac{\partial H^{(i)}}{\partial u} (t) = 0$

, for all

$t \in [t_{0}, t_{f}]$

The value of

$τ$

is usually selected ad hoc, possibly as a value that effects a certain value of

$Δ J_{a}$

or using a single variable search. The steepest descent algorithm can be found in detail in [137] and references therein.

C.5.2. Variation of Extremals

In the optimal control problem defined in the previous sections, the condition

$\frac{\partial H (x^{*} (t), u^{*} (t), p^{*} (t))}{\partial u} = 0$

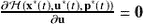
was used to obtain a set of differential equations of the form

$\dot{x} (t) = a (x (t), p (t), t)$

and

$\dot{p} (t) = d (x (t), p (t), t)$

(for a first-order system), where the admissible state/control values were not bounded. In order to proceed with a numerical computation of the optimal trajectory, the value of the initial

$p^{(0)} (t_{0})$

needs to be guessed and used for integrating and further obtaining every succeeding trajectory. For this purpose, Newton’s method [11] may be employed, which for the case of

$2 n$

differential equations would yield the matrix equation

$p^{(i + 1)} (t_{0}) = p^{(i)} (t_{0}) - {[P_{p} (p^{(i)} (t_{0}), t_{f})]}^{- 1} p^{(i)} (t_{f}),$

(C.50)

where the costate influence function matrix

$P_{p}$

is given by

$P_{p} (p^{(i)} (t_{0}), t) = {[\begin{matrix} \frac{\partial p_{1} (t)}{\partial p_{1} (t_{0})} & \frac{\partial p_{1} (t)}{\partial p_{2} (t_{0})} & . . . & \frac{\partial p_{1} (t)}{\partial p_{n} (t_{0})} \\ . . . & . . . & . . . & . . . \\ \frac{\partial p_{n} (t)}{\partial p_{1} (t_{0})} & \frac{\partial p_{n} (t)}{\partial p_{2} (t_{0})} & . . . & \frac{\partial p_{n} (t)}{\partial p_{n} (t_{0})} \end{matrix}]}_{p^{(i)} (t_{0})},$

(C.51)

which is appropriate only if the desired value of the final costate is zero, which in addition occurs if the term

$h (x (t_{f}))$

is missing from performance measure (C.3). If however,

$h (x (t_{f}))$

exists, then

$p^{(i + 1)} (t_{0}) = p^{(i)} (t_{0}) - {{[[\frac{\partial^{2} h}{\partial x^{2}} (x (t_{f}))] P_{x} (p^{(i)} (t_{0}), t_{f}) - P_{p} (p^{(i)} (t_{0}), t_{f})]}_{i}}^{- 1} \times {[p^{(i)} (t_{f}) - \frac{\partial h}{\partial x} (x (t_{f}))]}_{i},$

(C.52)

where now the state influence function matrix is given by

$P_{x} (p^{(i)} (t_{0}), t) = {[\begin{matrix} \frac{\partial x_{1} (t)}{\partial p_{1} (t_{0})} & \frac{\partial x_{1} (t)}{\partial p_{2} (t_{0})} & . . . & \frac{\partial x_{1} (t)}{\partial p_{n} (t_{0})} \\ . . . & . . . & . . . & . . . \\ \frac{\partial x_{n} (t)}{\partial p_{1} (t_{0})} & \frac{\partial x_{n} (t)}{\partial p_{2} (t_{0})} & . . . & \frac{\partial x_{n} (t)}{\partial p_{n} (t_{0})} \end{matrix}]}_{p^{(i)} (t_{0})},$

(C.53)

and the influence function matrices can be determined as in [137] (pp. 348–349). The appropriate initial conditions for influence matrices are

$P_{x} (p^{(i)} (t_{0}), t_{0}) = \frac{\partial x (t_{0})}{\partial p (t_{0})} ∣_{p^{(i)} (t_{0})} = 0,$

$P_{p} (p^{(i)} (t_{0}), t_{0}) = \frac{\partial P (t_{0})}{\partial p (t_{0})} ∣_{p^{(i)} (t_{0})} = I .$

A detailed description of the steps of the variation of extremals algorithm is provided also in [137] and references therein.

C.5.3. Quasilinearization

Consider a linear two-point boundary-value problem to be solved,

$\dot{x} (t) = a_{11} (t) x (t) + a_{12} (t) p (t) + e_{1} (t), x (t_{0}) = x_{0},$

(C.54)

$\dot{p} (t) = a_{21} (t) x (t) + a_{22} (t) p (t) + e_{2} (t), p (t_{f}) = p_{f},$

(C.55)

where

$a_{11}, a_{12}, a_{21}, a_{22}, e_{1}, e_{2}$

are known functions and

$t_{0}, t_{f}, x_{0}, p_{f}$

are known constants.

For this system, a solution can be obtained by numerical integration and initial conditions

$x^{''} (t_{0}) = x_{0}, p^{''} (t_{0}) = 0$

, while a particular solution to the nonhomogeneous system can be again obtained with numerical integration, with initial conditions

$x^{p} (t_{0}) = x_{0}, p^{p} (t_{0}) = 0$

. Combining these two solutions, a third one may be obtained for the linear two-point boundary-value problem, in terms of the solution of a linear algebraic equation.

The quasilinearization approach is based on the linearization of the reduced state-costate equations, which in turn is based on the Taylor series expansion about the initial state-costate variables. To demonstrate this process, we assume one state and one costate variable and solve

$\frac{\partial H}{\partial u} = 0$

for

$u (t)$

. Then we substitute in the state-costate equations to obtain

$\dot{x} (t) = a (x (t), p (t), t)$

and

$\dot{p} (t) = d (x (t), p (t), t)$

, where

$a, d$

are nonlinear functions, and

$x^{(0)} (t), p^{(0)} (t), t \in [t_{0}, t_{f}]$

are known trajectories. The linearization using Taylor series expansion about

$x^{(0)} (t), p^{(0)} (t)$

and some basic calculus yields

${\dot{x}}^{(1)} (t) = a_{11} (t) x^{(t)} (t) + a_{12} (t) p^{(1)} (t) + e_{1} (t),$

(C.56)

${\dot{p}}^{(1)} (t) = a_{21} (t) x^{(t)} (t) + a_{22} (t) p^{(2)} (t) + e_{2} (t),$

(C.57)

where

$a_{11} (t) = \frac{\partial a}{\partial x} (x^{(0)} (t), p^{(0)} (t), t) a_{12} (t) = \frac{\partial a}{\partial p} (x^{(0)} (t), p^{(0)} (t), t),$

$a_{21} (t) = \frac{\partial d}{\partial x} (x^{(0)} (t), p^{(0)} (t), t) a_{22} (t) = \frac{\partial d}{\partial p} (x^{(0)} (t), p^{(0)} (t), t),$

$e_{1} (t) = a (x^{(0)} (t), p^{(0)} (t), t) - [\frac{\partial a}{\partial x} (x^{(0)} (t), p^{(0)} (t), t)] x^{(0)} (t) - \frac{\partial a}{\partial p} (x^{(0)} (t), p^{(0)} (t), t) p^{(0)} (t),$

$e_{2} (t) = d (x^{(0)} (t), p^{(0)} (t), t) - [\frac{\partial d}{\partial x} (x^{(0)} (t), p^{(0)} (t), t)] x^{(0)} (t) - \frac{\partial d}{\partial p} (x^{(0)} (t), p^{(0)} (t), t) p^{(0)} (t)$

are all known functions.

Detailed implementation steps (in the form of pseudocode) of the quasilinearization approach can be found in [137]. Additional properties and aspects of its operation and behavior can be also found in [137] and references therein.

The three previous iterative methods regard in general unconstrained, nonlinear, two-point boundary-value problems. They solve problems (more accurately a sequence of partial problems that should converge to the analyzed problem), where one or more necessary conditions is/are initially violated, but eventually satisfied if the iterative process converges. Trying several different initial guesses, or if the iterative procedure converges to the same control and trajectory for a variety of initial guesses, there exists some assurance that a global minimum has been determined. A table summary of the features of these three approaches, such as the initial guess, storage requirements, required computations, is provided in [137].

C.5.4. Gradient Projection

Gradient projection methods, on the other hand, are iterative numerical procedures for finding extrema of function of several variables, which are required to satisfy various constraining relations.

Assume a convex function

$f (y)$

defined in the region

$R$

, which means that it satisfies

$(1 - θ) f (y^{(0)}) + θ f (y^{(1)}) \geq f ((1 - θ) y^{(0)} + θ y^{(1)}),$

for all

$0 \leq θ \leq 1$

$y^{(0)}, y^{(1)} \in R$

. Variables

$y_{1}, y_{2}, . . . y_{k}$

are constrained by

$L$

linear inequalities of the form

$\sum_{j = 1}^{K} n_{j i} y_{j} - v_{i} \geq 0$

(

$n_{i} = {[n_{1 i} n_{2 i} . . . n_{k i}]}^{T}$

). If

$N_{L} = [n_{1} n_{2} . . . n_{L}]$

are orthonormal vectors, defined as

$v_{L} = [v_{1} v_{2} . . . v_{L}]$

and

$λ (y) = {[λ_{1} (y) λ_{2} (y) . . . λ_{L} (y)]}^{T}$

, then the set of linear constraints can be expressed as

$n_{i}^{T} y - v_{i} \geq λ_{i} (y) \geq 0$

, for

$i = 1, 2, . . ., L$

(

$N_{L}^{T} y - v_{L} = λ (y) \geq 0$

) and points of the form

$λ_{i} (y)$

will lie in a hyperplane

$H_{i}$

in the

$K$

-dimensional space.

Suppose

$y$

is a point

$N_{q}^{T} y - v_{q} = 0$

(intersection of

$q$

linearly independent hyperplanes) and points

$w$

are such that

$N_{q}^{T} w = 0$

(intersection of

$q$

linearly independent hyperplanes, each of which contains the origin). Then

$Q$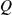

(denoting the intersection defined above by

$N_{q}^{T} w = 0$

, which is a

$(K - q)$

-dimensional subspace of

$E^{K}$

being the

$K$

-dimensional Euclidean space) and

$Q^{'}$

(the intersection of hyperplanes

$H_{1}, H_{2}, . . . ., H_{q}$

) are orthogonal differing only by vector

$v_{q}$

. Then, the following two

$K \times K$

symmetric matrices can be defined as

${\tilde{P}}_{q} = N_{q} {[N_{q}^{T} N_{q}]}^{- 1} N_{q}^{T},$

$P_{q} = I - N_{q} {[N_{q}^{T} N_{q}]}^{- 1}] N_{q}^{T} = I - {\tilde{P}}_{q},$

where the first is the projection matrix that takes any vector in

$E^{K}$

into

$\tilde{Q}$

and the second a projection matrix that takes any vector

$E^{K}$

into

$Q$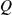

. Thus,

$\tilde{Q}$

is a

$q$

-dimensional subspace of

$E^{K}$

spanned by

$n_{1}, . . ., n_{L}$

constituting the space

$N_{q}$

Assuming that

$f$

is convex with continuous second partial derivatives in a closed and bounded convex region

$R$

$E^{K}$

, and letting

$y^{*}$

be a boundary point of

$R$

which lies on exactly

$q$

$1 \leq q \leq K$

hyperplanes that are assumed to be linearly independent with

$Q^{'}$

denoting the intersection of these hyperplanes, then point

$y^{*}$

is a constrained global minimum if and only if

$P_{q} [- \frac{\partial f}{\partial y} (y^{*})] = 0 and {[N_{q}^{T} N_{q}]}^{- 1}] N_{q}^{T} [- \frac{\partial f}{\partial y} (y^{*})] \leq 0 .$

(C.58)

$y^{*}$

is an interior point in

$R$

, a necessary and sufficient condition is

$\frac{\partial f}{\partial y} (y^{*}) = 0$

Exploiting the above, the optimal trajectories of a constrained optimal control problem can be determined using gradient projection. More specifically, it is desired to find an admissible control history

$u^{*}$

causing

$\dot{x} (t) = a (x (t), u (t))$

$x (t_{0}) = x_{0}$

to follow admissible

$x^{*}$

that minimizes the performance measure

$J = h (x (t_{f})) + \int_{t_{0}}^{t_{f}} g (x (t), u (t)) d t$

, with

$t_{0} = 0$

$t_{f}$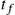

specified, and constraints

$M_{i -} \leq u_{i} (t) \leq M_{i +}, t \in [0, t_{f}], i = 1, 2, . . ., m,$

(C.59)

$S_{i -} \leq x_{i} (t) \leq S_{i +}, t \in [0, t_{f}], i = 1, 2, . . ., n,$

(C.60)

$x_{i} (t_{j}) = T_{i j}, t_{j} specified, i = 1, 2, . . ., n .$

(C.61)

Approximating the state differential equations by the difference equations (which can be nonlinear) we obtain

$x (t + Δ t) \approx x (t) + a (x (t), u (t)) \times Δ t, t = 0, Δ t, 2 Δ t, . . ., N Δ t .$

The latter can be written together with the discrete performance metric in the simpler form

$x (k + 1) = x (k) + a (x (k), u (k)) Δ t = a_{D} (x (k), u (k)),$

(C.62)

$J_{D} = h (x (N)) + Δ t \sum_{k = 0}^{N - 1} g (x (k), u (k)) .$

(C.63)

Thus, it is required to find

$(N n + N m)$

variables that minimize

$J_{D}$

and satisfy the approximate state equations and constraints. If the state equations are nonlinear, then, they can be linearized about a nominal state-control history, followed by solving a sequence of linearized problems.

The state-control history is considered known,

$(x^{(i)} (0), x^{(i)} (1), . . . x^{(i)} (N); u^{(i)} (0), u^{(i)} (1), . . ., u^{(i)} (N - 1)),$

and an initial state-control history can be guessed in the form

$x^{(i + 1)} (k + 1) = A (k) x^{(i + 1)} (k) + B (k) u^{(i + 1)} (k) + c (u),$

(C.64)

where

$A, B, c$

are known time-varying matrices. Since

$x (0) = x_{0}$

is specified,

$x^{(i)} (0) = x_{0}$

for all

$i$

, and thus in the general case

$x^{(i + 1)} (k + 1) = A (k) x_{H} + c (k) + A (k) . . . A (1) B (0) u^{(i + 1)} (0) + . . . . = x_{H} (k + 1) + D_{0}^{k + 1} u^{(i_{+} 1)} (0) + . . . + D_{k}^{k + 1} u^{(i_{+} 1)} (k) = x_{H} (k + 1) + \sum_{ℓ = 0}^{N - 1} [D_{ℓ}^{k + 1} u^{(i + 1)} (ℓ)],$

(C.65)

where

$x_{k} (k + 1) = A (k) x_{H} (k) + c (k), x_{H} (0) = x_{0}$

and

$D_{ℓ^{k + 1}} = {\begin{matrix} A (k) A (k - 1) . . . A (ℓ + 1) B (ℓ), & k > ℓ \\ B (ℓ), & k = ℓ \\ 0, & k < ℓ \end{matrix} .$

In this fashion, the entire discrete state history can be written in terms of the discrete control history, as

$X^{(i + 1)} = D_{0} U^{(i + 1)} + X_{0}$

. If there are inequality constraints involving the states

$[\begin{matrix} S_{1 -} \\ S_{2 -} \\ . . . \\ S_{n -} \end{matrix}] \leq x (k) \leq [\begin{matrix} S_{1 +} \\ S_{2 +} \\ . . . \\ S_{n +} \end{matrix}], k = 0, 1, . . ., N$

, these can be expressed as linear constraints involving only control values

$[\begin{matrix} S_{1 -} \\ S_{2 -} \\ . . . \\ S_{n -} \end{matrix}] \leq D_{0}^{k} u^{(i + 1)} (0) + . . . + D_{N - 1}^{k} u^{(i + 1)} (N - 1) + x_{H} (k) \leq [\begin{matrix} S_{1 +} \\ S_{2 +} \\ . . . \\ S_{n +} \end{matrix}], k = 0, 1, . . ., N .$

Consequently, the problem to be solved is to find the control values that satisfy the constraints

$[\begin{matrix} M_{1 -} \\ M_{2 -} \\ . . . \\ M_{m -} \end{matrix}] \leq u^{(i + 1)} (k) \leq [\begin{matrix} M_{1 +} \\ M_{2 +} \\ . . . \\ M_{m +} \end{matrix}], k = 0, 1, . . ., N,$

$[\begin{matrix} T_{1 j} \\ T_{2 j} \\ . . . \\ T_{n j} \end{matrix}] \leq D_{0}^{j} u^{(i + 1)} (0) + . . . + D_{N - 1}^{j} u^{(i + 1)} (N - 1) + x_{H} (j), j specified,$

and minimize the function of

$N m$

variables given by

$J_{D} = h (U^{(i + 1)}) + Δ t \sum_{k = 0}^{N - 1} g (U^{(i + 1)}) .$

A summary of the gradient projection algorithm for determining optimal trajectories can be found in [137] and references therein.

..................Content has been hidden....................

You can't read the all page of ebook, please click here login for view all page.

Table of Contents for C.5. Numerical Determination of Optimal Trajectories

Create new playlist

Sign In

Sign Up

C.5. Numerical Determination of Optimal Trajectories

C.5.1. Steepest Descent

C.5.2. Variation of Extremals

C.5.3. Quasilinearization

C.5.4. Gradient Projection

Table of Contents for
C.5. Numerical Determination of Optimal Trajectories