B.3. Markovian Systems in Equilibrium

Search in book...
Toggle Font Controls
Create new playlist

Name your new playlist

Playlist description (optional)
Sign In

Email address

Password

Forgot Password?

or

Continue with Facebook

Continue with Google
Sign Up

Full Name

Email address

Confirm Email Address

Password

or

Continue with Facebook

Continue with Google

B.3. Markovian Systems in Equilibrium

B.3.1. Discrete-time Markov Chains

A Markov chain discrete-time Markov chain - DTMC is a random process that undergoes transitions from one state to another on a state space. It must possess the “memorylessness” property , namely, that the probability distribution of the next state depends only on the current state and not on the sequence of events that preceded it. The material presented in this subsection will be useful for the study of queuing systems treated in the later subsections of Appendix B.3 and Chapters 4 and 5.

More formally, a stochastic process

{X_{n}, n = 0, 1, 2, \dots}

${X_{n}, n = 0, 1, 2, \dots}$

that takes a finite or countable number of possible values is said to be in state

i

$i$

at time

n

$n$

X_{n} = i

$X_{n} = i$

. We assume that there is a fixed probability

P_{i j}

$P_{i j}$

that if the process is in state

i

$i$

it will next be in state

j

$j$

$Pr {X_{n + 1} = j ∣ X_{n} = i, X_{n - 1} = i_{n - 1}, \dots, X_{1} = i_{1}, X_{0} = i_{0}} = Pr {X_{n + 1} = j ∣ X_{n} = i} = P_{i j}$ $Pr {X_{n + 1} = j ∣ X_{n} = i, X_{n - 1} = i_{n - 1}, \dots, X_{1} = i_{1}, X_{0} = i_{0}} = Pr {X_{n + 1} = j ∣ X_{n} = i} = P_{i j}$

(B.2)

for all states

i_{0}, i_{1}, \dots, i_{n - 1}, i, j

$i_{0}, i_{1}, \dots, i_{n - 1}, i, j$

and all

n \geq 0

$n \geq 0$

. Such a stochastic process is known as a (discrete) Markov chain. The Markovian property, expressed by Eq. (B.2), is that the conditional distribution of any future state

X_{n + 1}

$X_{n + 1}$

given the past states

X_{0}, X_{1}, \dots, X_{n - 1}

$X_{0}, X_{1}, \dots, X_{n - 1}$

and the present state

X_{n}

$X_{n}$

is independent of the past states and depends only on the present state. Thus, a Markov chain is a sequence of random variables

X_{1}, X_{2}, X_{3}, \dots

$X_{1}, X_{2}, X_{3}, \dots$

with the Markov property. Since the process must make a transition into some state,

\sum_{j = 0}^{\infty} P_{i j} = 1, i = 0, 1, \dots, P_{i j} \geq 0, i, j \geq 0

$\sum_{j = 0}^{\infty} P_{i j} = 1, i = 0, 1, \dots, P_{i j} \geq 0, i, j \geq 0$

A Markov chain is said to be homogeneous in time if the transition probability between two distinct states depends only on the time step difference, i.e.

Pr {X_{m + n} = j ∣ X_{m} = i} = P_{i j}^{n}

$Pr {X_{m + n} = j ∣ X_{m} = i} = P_{i j}^{n}$

. Here, we focus on homogeneous Markov processes.

Eq. (B.2) defines the so-called one-step transition probabilities , namely probabilities that describe the transition of the chain in one time step. These transitions can be depicted via a state diagram, where a state diagram is a directed graph used to picture the state transitions. The states that the chain transitions to will be called neighboring states. Similarly, the

n

$n$

-step probabilities that the process will be in state

j

$j$

starting at

i

$i$

after

n

$n$

successive transitions (

n

$n$

successive time steps) are

$P_{i j}^{n} = Pr {X_{n + m} = j ∣ X_{m} = i}, n, i, j \geq 0 .$ $P_{i j}^{n} = Pr {X_{n + m} = j ∣ X_{m} = i}, n, i, j \geq 0 .$

(B.3)

In order to compute the

n

$n$

-step transition probabilities, the Chapman-Kolmogorov equations shown in the following can be employed:

$P_{i j}^{n + m} = \sum_{k = 0}^{\infty} P_{i k}^{n} P_{k j}^{m}, for all n, m \geq 0, all i, j .$ $P_{i j}^{n + m} = \sum_{k = 0}^{\infty} P_{i k}^{n} P_{k j}^{m}, for all n, m \geq 0, all i, j .$

(B.4)

f_{i j}^{n}

$f_{i j}^{n}$

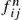is the probability that starting in state

i

$i$

, the first transition to

j

$j$

occurs at time

n

$n$

, then state

j

$j$

is said to be recurrent if

f_{j j} = 1

$f_{j j} = 1$

, which means that starting at state

j

$j$

the process will return to state

j

$j$

with probability 1 for some time

n

$n$

(

f_{j j} = \sum_{n = 1}^{\infty} f_{i j}^{n}

$f_{j j} = \sum_{n = 1}^{\infty} f_{i j}^{n}$

). A state is transient if

f_{j j} < 1

$f_{j j} < 1$

. If state

j

$j$

is recurrent and

μ_{j} = \sum_{n = 1}^{\infty} n f_{j j}^{n}

$μ_{j} = \sum_{n = 1}^{\infty} n f_{j j}^{n}$

denotes the expected number of transitions needed to return to start

j

$j$

(mean recurrence time - expected return time in state

j

$j$

), then state

j

$j$

is positive recurrent if

μ_{j} < \infty

$μ_{j} < \infty$

and null recurrent if

μ_{j} = \infty

$μ_{j} = \infty$

. A state

j

$j$

is said to be accessible from a state

i

$i$

(written

i \to j

$i \to j$

) if a system that started in state

i

$i$

has a nonzero probability of transitioning into state

j

$j$

at some point (

Pr {X_{n} = j ∣ X_{0} = i} = P_{i j}^{n} > 0

$Pr {X_{n} = j ∣ X_{0} = i} = P_{i j}^{n} > 0$

for some

n > 0

$n > 0$

). A state

i

$i$

has period

k

$k$

if any return to state

i

$i$

must occur in multiples of

k

$k$

time steps. If

k = 1

$k = 1$

, then the state is said to be aperiodic, namely, returns to state

i

$i$

can occur at irregular times. A Markov chain is aperiodic if every state is aperiodic and an irreducible Markov chain only needs one aperiodic state to imply all states are aperiodic. A state

i

$i$

is called absorbing if it is impossible to leave this state.

A state

i

$i$

is said to be ergodic if it is aperiodic and positive recurrent, namely, if it is recurrent, has a period of 1, and it has finite mean recurrence time. If all states in an irreducible Markov chain are ergodic, then the chain is said to be ergodic. It can be shown that a finite state irreducible Markov chain is ergodic if it has an aperiodic state.

If an irreducible aperiodic Markov chain is positive recurrent, then we can define as

π_{j} = {lim}_{n \to \infty} P_{i j}^{n}

$π_{j} = {lim}_{n \to \infty} P_{i j}^{n}$

, where

P_{i j}^{n}

$P_{i j}^{n}$

is obtained from (B.3) for

n = 1

$n = 1$

. Let

S

$S$

denote the set of possible states that the process can make a transition to. If there is a probability distribution over states

π

$π$

such that

$π_{j} = \sum_{i \in S} π_{i} Pr {X_{n + 1} = j ∣ X_{n} = i}$ $π_{j} = \sum_{i \in S} π_{i} Pr {X_{n + 1} = j ∣ X_{n} = i}$

(B.5)

for every state

j

$j$

and every time

n

$n$

then

π

$π$

is a stationary distribution of the Markov chain. An irreducible chain has a stationary distribution if and only if all of its states are positive recurrent. In that case,

π

$π$

is unique and related to the expected return time

M_{j}

$M_{j}$

π_{j} = \frac{C}{M_{j}}

$π_{j} = \frac{C}{M_{j}}$

, where

C

$C$

is a normalizing constant independent of the state. The chain converges to the stationary distribution regardless of the initial state distribution. Such

π

$π$

is called the equilibrium distribution of the chain. For a finite state space, a stationary distribution

π

$π$

is a (row) vector, whose entries are non-negative and sum to 1, it is unchanged by the operation of transition matrix

P

$P$

and it is defined by

π P = π

$π P = π$

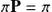. In addition,

0 \leq π_{j} \leq 1

$0 \leq π_{j} \leq 1$

and

\sum_{j \in S} π_{j} = 1

$\sum_{j \in S} π_{j} = 1$

. Then the transition probability distribution can be represented by the transition matrix

P

$P$

, with the

(i, j)

$(i, j)$

th element of

P

$P$

equal to

π_{j} = Pr {X_{n + 1} = j ∣ X_{n} = i}

$π_{j} = Pr {X_{n + 1} = j ∣ X_{n} = i}$

B.3.2. Continuous-time Markov Processes

A continuous-time Markov process may be in one of the finite or infinite many (however countably infinite many) states at a time. The probability that the process transitions from state

i

$i$

j

$j$

at time

t_{0} + t

$t_{0} + t$

is defined as

Pr {X (t_{0} + t) = j ∣ X (t_{0}) = j}

$Pr {X (t_{0} + t) = j ∣ X (t_{0}) = j}$

and it is independent of the behavior of

X (t)

$X (t)$

prior to

t_{0}

$t_{0}$

. If

X (t)

$X (t)$

is a homogeneous Markov process, the above probability depends only on the elapsed time required for the transition and not the initial time

t_{0}

$t_{0}$

. Thus in this case,

P_{i j} (t) = Pr {X (t_{0} + t) = j ∣ X (t_{0}) = i}

$P_{i j} (t) = Pr {X (t_{0} + t) = j ∣ X (t_{0}) = i}$

P_{i j} (t) = Pr {X (t) = j ∣ X (0) = i}

$P_{i j} (t) = Pr {X (t) = j ∣ X (0) = i}$

, denoted by state transition rates as opposed to the corresponding state transition probabilities in the discrete case (

P_{i j}^{n}

$P_{i j}^{n}$

). The state transition rates are obtained as derivatives of the state transition probabilities at

t = 0

$t = 0$

. Markov processes, in general, are characterized by the basic property that the past has no influence on the future if the present is specified and can be expressed in the continuous form as

$Pr {X (n) = x_{n} ∣ X (n - 1), \dots . X (1)} = Pr {X (n) = x_{n} ∣ X (n - 1)} .$ $Pr {X (n) = x_{n} ∣ X (n - 1), \dots . X (1)} = Pr {X (n) = x_{n} ∣ X (n - 1)} .$

(B.6)

All Markov processes share the interesting property that the time it takes for a change of state, called sojourn time is an exponentially distributed random variable [174].

The initial probability distribution of state

i

$i$

is given by

P_{i} (0) = P {X (0)} = i

$P_{i} (0) = P {X (0)} = i$

, defined analogously for the rest of states, and the unconditional probability that the process is in state

j

$j$

at time

t

$t$

is defined as

P_{j} (t) = \sum_{i} P_{i} (0) P_{i j} (t)

$P_{j} (t) = \sum_{i} P_{i} (0) P_{i j} (t)$

. For arbitrary

t

$t$

and

s

$s$

, the continuous version of the Chapman-Kolmogorov equations is given by

$P_{i j} (t + s) = P {X (t + s) = j ∣ X (0) = i} = \sum_{k} P_{i k} (t) P_{k j} (s) .$ $P_{i j} (t + s) = P {X (t + s) = j ∣ X (0) = i} = \sum_{k} P_{i k} (t) P_{k j} (s) .$

(B.7)

B.3.3. Birth-and-Death Processes

The birth-death process is a special case of continuous-time Markov chain (CTMC), where the state transitions are of two types only, namely, “births,” which increase the state variable by one and “deaths,” which decrease the state by one [174]. A typical example is that of some banks which have a security door that allows only one person at a time to enter/leave the bank. In this case, irrespective of the system state, at each time instant the next event is either the arrival of a customer in the bank, or the departure of a customer that completed the required service and leaves the building. In these and similar cases, when a birth occurs, the process goes from state

n

$n$

n + 1

$n + 1$

. When a death occurs, the process goes from state

n

$n$

to state

n - 1

$n - 1$

. The state diagram evolution for such a process is depicted in Fig. B.3. Such processes are specified by their birth rates

{λ_{i}}_{i = 0 \dots \infty}

${λ_{i}}_{i = 0 \dots \infty}$

and death rates

{μ_{i}}_{i = 1 \dots \infty}

${μ_{i}}_{i = 1 \dots \infty}$

. A pure birth process is a birth-death process where

μ_{i} = 0 for all i \geq 0

$μ_{i} = 0 for all i \geq 0$

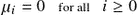, while a pure death process is a birth-death process where

λ_{i} = 0 for all i \geq 0

$λ_{i} = 0 for all i \geq 0$

. A (homogeneous) Poisson process is a pure birth process where

λ_{i} = λ for all i \geq 0

$λ_{i} = λ for all i \geq 0$

Fig. B.3 — FIGURE B.3 State diagram for the birth-death process.

The global balance equations (also known as full balance equations) are a set of equations that in principle can be solved to give the equilibrium distribution of a Markov process (when such a distribution exists). For a continuous-time Markov process with state space

S

$S$

, transition rate from state

i

$i$

j

$j$

given by

q_{i j}

$q_{i j}$

and equilibrium distribution given by

π

$π$

, the global balance equations are given for every state

i

$i$

S

$S$

$\sum_{j \in S {i}} π_{i} q_{i j} = \sum_{j \in S {i}} π_{j} q_{j i},$ $\sum_{j \in S {i}} π_{i} q_{i j} = \sum_{j \in S {i}} π_{j} q_{j i},$

(B.8)

where

π_{i} q_{i j}

$π_{i} q_{i j}$

represents the probability flux for state

i

$i$

to state

j

$j$

For a CTMC with transition rate matrix

Q = [q_{i j}]

$Q = [q_{i j}]$

, if

π_{i}

$π_{i}$

can be found such that for every pair of states

i

$i$

and

j

$j$

π_{i} q_{i j} = π_{j} q_{j i}

$π_{i} q_{i j} = π_{j} q_{j i}$

holds, then the global balance equations are satisfied and

π

$π$

is the stationary distribution of the process. If such a solution can be found, the resulting equations are usually much easier than directly solving the global balance equations. Furthermore, a CTMC is reversible if and only if the detailed balance conditions are satisfied for every pair of states

i

$i$

and

j

$j$

In queuing theory, the birth-death process is the most fundamental example of a queuing model. In the following, we provide a brief overview of simple and characteristic birth-death queuing systems that have particular interest for the analysis of queuing networks and some of the methodologies presented in this book, especially in Chapter 4. The rest of the systems presented in this subsection with an infinite queue are all characteristic examples of birth-death systems defined in this subsection.

B.3.4. The $M ∕ M ∕ 1$ $M ∕ M ∕ 1$ Queuing System

The

M ∕ M ∕ 1

$M ∕ M ∕ 1$

queue is a system having a single server, where arrivals are determined by a Poisson process and job service times have an exponential distribution. Arrivals are assumed to occur at rate

λ

$λ$

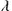and service times have an exponential distribution with mean

1 ∕ μ

$1 ∕ μ$

. The single server operates according to a FIFO discipline. When the service of a customer is complete, the customer at the head of the queue leaves the storage space entering the server, the customer that completed service leaves the systems, and the number of customers in the system reduces by one. The buffer (queue) of the system is of infinite size.

The model is considered stable only if

λ < μ

$λ < μ$

. If, on average, arrivals happen faster than service completions the queue will grow indefinitely long and the system will not have a stationary distribution. Assuming

ρ = λ ∕ μ

$ρ = λ ∕ μ$

for the utilization of the buffer and require

ρ < 1

$ρ < 1$

for the queue to be stable,

ρ

$ρ$

represents the average proportion of time for which the server is occupied. In order to see this more intuitively, consider the version of Little’s law with respect to the server, which gives the average number of customers in the server

N_{w}

$N_{w}$

with respect to the arrival rate

λ

$λ$

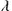and the mean service time

1 ∕ μ

$1 ∕ μ$

N w = \frac{λ}{μ} = ρ

$N w = \frac{λ}{μ} = ρ$

. For the

M ∕ M ∕ 1

$M ∕ M ∕ 1$

system to be stable, at most one customer at a time should be in service, as expected by the definition of its operation.

The corresponding state diagram is of birth-death type, similar to Fig. B.3. Useful closed-form expressions may be obtained for various quantities of interest. More details on the analysis methodology of the

M ∕ M ∕ 1

$M ∕ M ∕ 1$

queue can be found in [25,142], etc. The most useful results obtained include the following:

• The steady-state probability distribution is given by

p_{n} = ρ^{n} (1 - ρ), n = 0, 1, \dots

$p_{n} = ρ^{n} (1 - ρ), n = 0, 1, \dots$

• The average number of customers in the system in the steady state is

N = \frac{λ}{μ - λ}

$N = \frac{λ}{μ - λ}$

• The average system delay per customer (waiting time plus service time) is

T = \frac{1}{μ - λ}

$T = \frac{1}{μ - λ}$

• The average waiting time in queue is

W = \frac{ρ}{μ - λ}

$W = \frac{ρ}{μ - λ}$

• The average number of customers in the queue is

N_{Q} = \frac{ρ^{2}}{1 - ρ}

$N_{Q} = \frac{ρ^{2}}{1 - ρ}$

Additional quantities of interest can be obtained via analysis as shown in [25] and other references targeted explicitly to queuing theory analysis [33,36,90,142,209,211,229].

B.3.5. The $M ∕ M ∕ m$ $M ∕ M ∕ m$ System and Other Multiserver Queuing Systems

The

M ∕ M ∕ 1

$M ∕ M ∕ 1$

queue is a very simple system that emerges frequently in various occasions. However, oftentimes, multiserver systems are employed. In this subsection, we overview the most fundamental of them. As with the

M ∕ M ∕ 1

$M ∕ M ∕ 1$

system, for all these multiserver systems, it is possible to derive a set of equations from the corresponding state transition diagram and solve for the steady-state (equilibrium) probabilities. Using Little’s law allows computing the average delay per customer and other quantities of interest.

The $M ∕ M ∕ m$ $M ∕ M ∕ m$ queuing system

The

M ∕ M ∕ m

$M ∕ M ∕ m$

system is similar to the

M ∕ M ∕ 1

$M ∕ M ∕ 1$

with respect to the arrival process (Poisson), the independence of service times, and the exponentially distributed and independent interarrival times. However, this system has

m

$m$

parallel servers, meaning that a customer at the head of the queue (ready to receive service) can be routed to any of the server currently available, once a customer completes service in one of them.

Applying the analysis methodology of balance equations, the corresponding outcomes for the quantities of interest obtained in the

M ∕ M ∕ 1

$M ∕ M ∕ 1$

case are as follows:

• The probability that an arriving customer will find all servers buys and will be forced to queue is

P_{Q} = \frac{p_{0} {(m ρ)}^{m}}{m! (1 - ρ)}

$P_{Q} = \frac{p_{0} {(m ρ)}^{m}}{m! (1 - ρ)}$

, where

p_{0}

$p_{0}$

is given by the expression

$p_{0} = {[1 + \sum_{n = 1}^{m - 1} \frac{{(m ρ)}^{n}}{n!} + \sum_{n = m}^{\infty} \frac{{(m ρ)}^{n}}{m!} \frac{1}{m^{n - m}}]}^{- 1} .$ $p_{0} = {[1 + \sum_{n = 1}^{m - 1} \frac{{(m ρ)}^{n}}{n!} + \sum_{n = m}^{\infty} \frac{{(m ρ)}^{n}}{m!} \frac{1}{m^{n - m}}]}^{- 1} .$

(B.9)

• The average number of customers in the system in the steady state is

N = m ρ + \frac{ρ P_{Q}}{1 - ρ}

$N = m ρ + \frac{ρ P_{Q}}{1 - ρ}$

• The average system delay per customer (waiting time plus service time) is

T = \frac{1}{μ} + \frac{P_{Q}}{m μ - λ}

$T = \frac{1}{μ} + \frac{P_{Q}}{m μ - λ}$

• The average waiting time in queue is

W = \frac{ρ P_{Q}}{λ (1 - ρ)}

$W = \frac{ρ P_{Q}}{λ (1 - ρ)}$

• The average number of customers in the queue is

N_{Q} = P_{Q} \frac{ρ}{1 - ρ}

$N_{Q} = P_{Q} \frac{ρ}{1 - ρ}$

Now the utilization of the system is defined as

ρ = \frac{λ}{m μ} < 1

$ρ = \frac{λ}{m μ} < 1$

. In order to understand this stability condition for the system, note that now

m

$m$

servers operate in parallel each with an exponentially distributed service rate of

μ

$μ$

. This means that the combined server will be operating as a single server with service rate which will be the minimum of

m

$m$

exponential distributions. This has been proven to be again exponentially distributed with rate the sum of partial rates

m μ

$m μ$

. Thus, for the mean service time expression in the similar application of Little’s law that we performed for the

M ∕ M ∕ 1

$M ∕ M ∕ 1$

system, now for the case for the

M ∕ M ∕ m

$M ∕ M ∕ m$

would yield

\frac{λ}{m μ}

$\frac{λ}{m μ}$

The $M ∕ M ∕ \infty$ $M ∕ M ∕ \infty$ queuing system

In several cases, the available service has such a capacity that practically, any customer entering the system receives immediate service. Typical examples include web platforms receiving requests and serving them immediately (up to a certain point of course). In practice, the number of available servers is always finite. However, whenever the number of available servers is such that no queuing at all is observed, the system might well be considered as of an

M ∕ M ∕ \infty

$M ∕ M ∕ \infty$

type.

The

M ∕ M ∕ \infty

$M ∕ M ∕ \infty$

system can be considered as the limit of the

M ∕ M ∕ m

$M ∕ M ∕ m$

system when

m \to \infty

$m \to \infty$

. Consequently, in the limiting case where the number of servers is high (theoretically infinite number of servers),

m = \infty

$m = \infty$

, one obtains a

M ∕ M ∕ \infty

$M ∕ M ∕ \infty$

system for which the quantities of interest become the following:

• The average number of customers in the system in the steady state

N = \frac{λ}{μ}

$N = \frac{λ}{μ}$

• The average system delay per customer (waiting time plus service time)

T = \frac{1}{μ}

$T = \frac{1}{μ}$

Clearly, for such a system where a customer always finds an available empty server, there is no queuing and thus

N_{Q} = 0, W = 0

$N_{Q} = 0, W = 0$

. The response time for each arriving job is a single exponential distribution with parameter

μ

$μ$

as already explained and it thus coincides with the average system delay per customer given above. One should also notice that the stationary distribution of a more general queue with practical applications, the

M ∕ G ∕ \infty

$M ∕ G ∕ \infty$

queue where the service discipline can be arbitrary, but arrivals are Poisson and there exists an infinite number of servers, is the same as that of the

M ∕ M ∕ \infty

$M ∕ M ∕ \infty$

queue. This implies that an overprovisioned system, i.e. one with practically infinite number of servers, behaves the same irrespective of the service policy and the behavior is rather simple, since each customer is essentially served immediately. Thus, the mean number of customers in the system will be

N = \frac{λ}{μ}

$N = \frac{λ}{μ}$

in any case.

The steady-state distribution of the system is given by the expression

$p_{n} = {(\frac{λ}{μ})}^{n} \frac{e^{- λ ∕ μ}}{n!}, n = 0, 1, \dots$ $p_{n} = {(\frac{λ}{μ})}^{n} \frac{e^{- λ ∕ μ}}{n!}, n = 0, 1, \dots$

(B.10)

with

p_{0} = e^{- λ ∕ μ}

$p_{0} = e^{- λ ∕ μ}$

. From the above expression, it can be seen that the system is always stable, as no special constraint on the latter distribution is required. This is also intuitively verified by the fact that no matter how heavy the input load of customers, there are always available servers to satisfy it (infinite number). Thus, the number of customers waiting in the systems never grows arbitrarily and the system will be stable. In fact, it can be shown that the number of customers in the system is Poisson distributed even if the service time distribution is not exponential, e.g. in

M ∕ G ∕ \infty

$M ∕ G ∕ \infty$

[25]. The

M ∕ M ∕ \infty

$M ∕ M ∕ \infty$

system is also known as the Erlang-C model, as opposed to the Erlang-B that will be described in the following.

The $M ∕ M ∕ m ∕ m$ $M ∕ M ∕ m ∕ m$ queuing system

This system is identical to an

M ∕ M ∕ m

$M ∕ M ∕ m$

system with the difference that there is no queuing buffer space. The system consists of a facility where arrivals form a single queue and are governed by a Poisson process, there are

m

$m$

servers and job service times are exponentially distributed. Thus, the total capacity of the system is defined by the number of customers the system can serve instantaneously, which also means that when an arriving customer finds all

m

$m$

servers of the system busy, it is blocked from entering the system and thus discarded. For this reason, the model is called a loss system. The lost customers are said to be blocked. Practical examples of such systems are telephone exchanges, cellular phones, and other more general flow-service based systems.

In general, it is tough to obtain analytic expressions for the quantities of interest mentioned above for the other systems presented. However, it is possible to obtain the probability of

i

$i$

customers in the system and the blocking probability

p_{m}

$p_{m}$

, namely, the probability that an arriving customer will find all servers busy and will be discarded from the system

$p_{m} = \frac{{(λ ∕ μ)}^{m} ∕ m!}{\sum_{n = 0}^{m} {(λ ∕ μ)}^{n} ∕ n!} .$ $p_{m} = \frac{{(λ ∕ μ)}^{m} ∕ m!}{\sum_{n = 0}^{m} {(λ ∕ μ)}^{n} ∕ n!} .$

(B.11)

The latter is known as the Erlang B formula. This is also called the Erlang-B loss function and tabular solutions are usually provided in the related references. More details can be obtained in the corresponding references [25,33,36,90,142,209,211,229]. It should be noted that as

m \to \infty

$m \to \infty$

, the above distribution approaches the Poisson distribution of the

M ∕ M ∕ \infty

$M ∕ M ∕ \infty$

system, described above.

..................Content has been hidden....................

You can't read the all page of ebook, please click here login for view all page.

Table of Contents for B.3. Markovian Systems in Equilibrium

Create new playlist

Sign In

Sign Up

B.3. Markovian Systems in Equilibrium

B.3.1. Discrete-time Markov Chains

B.3.2. Continuous-time Markov Processes

B.3.3. Birth-and-Death Processes

Table of Contents for
B.3. Markovian Systems in Equilibrium