C.3. Finding Trajectories that Minimize Performance Measures
The problem classes presented in this section provide characteristic methodologies that can be exploited in broader optimal control problems, some of which have been exploited in this book. The rest can be used in various extensions to the study of intelligent attack strategies. In general, the Fundamental Theorem of Calculus of Variations can be exploited in optimal control theory for finding trajectories that minimize performance measures expressed as functionals. This is also the case in the corresponding modeling of malware diffusion in Chapter 6 and potential extensions to attack strategies.
C.3.1. Functionals of a Single Function
When the performance metric is a function of a single scalar function  in the class of continuous first derivatives, the functional can be written in the form
in the class of continuous first derivatives, the functional can be written in the form
 (C.14)
(C.14)
The objective is to find  for which
for which  has a relative extremum. Functions (curves) in
has a relative extremum. Functions (curves) in  that satisfy the end conditions are called admissible.
that satisfy the end conditions are called admissible.
When  ,
,  are free and
are free and 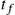 specified, the functional increment can be written as
specified, the functional increment can be written as
 (C.15)
(C.15)
which using a Taylor series expansion about  can be expressed as
can be expressed as
 (C.16)
(C.16)
By the fundamental theorem of calculus of variations, a necessary condition for  to be an extremal is
to be an extremal is
 (C.17)
(C.17)
The latter is an Euler differential equation. More specifically, it is a second order nonlinear ordinary and time-varying differential equation, which is hard to solve since it yields a two-point boundary-value problem with split boundary conditions.
When an extremal for the metric given in (C.15) with  specified and
specified and  free (which corresponds to the case where one boundary condition is given and the second is obtained from Euler equation-differential boundary condition) is required, the same approach as before applies as well, where now the metric functional is integrated by parts. It turns out that the necessary condition for
free (which corresponds to the case where one boundary condition is given and the second is obtained from Euler equation-differential boundary condition) is required, the same approach as before applies as well, where now the metric functional is integrated by parts. It turns out that the necessary condition for  to be an extremal is Eq. (C.17), and we may also obtain a natural boundary condition
to be an extremal is Eq. (C.17), and we may also obtain a natural boundary condition
![]() (C.18)
(C.18)
Thus, an extremal for a free endpoint problem is also an extremal for the fixed endpoint problem with the same endpoints and the same functional.
If one is given metric (C.15) and  are specified while
are specified while 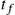 is free, Euler condition (C.17) is satisfied, along with the boundary condition
is free, Euler condition (C.17) is satisfied, along with the boundary condition

Finally, when an extremal is sought for metric (C.15) with  specified and
specified and  is free, again Euler condition (C.17) is satisfied, and when
is free, again Euler condition (C.17) is satisfied, and when 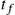 and
and  are unrelated,
are unrelated,  are independent and arbitrary yielding
are independent and arbitrary yielding 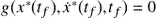 , while if
, while if 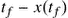 are related, e.g. in the form
are related, e.g. in the form  , then
, then  and the transversality condition
and the transversality condition
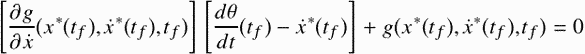 (C.19)
(C.19)
is obtained for solving the problem.
C.3.2. Functionals of Several Independent Functions
When the problem involves several independent functions, the performance metric can be written in the form
 (C.20)
(C.20)
with  all specified (fixed endpoints). This leads to a more convenient matrix form of the Euler equation
all specified (fixed endpoints). This leads to a more convenient matrix form of the Euler equation
 (C.21)
(C.21)
When the metric is given by (C.20) and  are specified, but
are specified, but  are free, then Euler condition (C.21) is satisfied along with boundary conditions at the final time of the form
are free, then Euler condition (C.21) is satisfied along with boundary conditions at the final time of the form
 (C.22)
(C.22)
C.3.3. Piecewise-smooth Extremals
When a function has piecewise continuous first derivatives except for a finite number of times (corner points), where  is discontinuous, then the functional of the performance metric can be defined in intervals that do not include the corner points. In this case, necessary conditions for
is discontinuous, then the functional of the performance metric can be defined in intervals that do not include the corner points. In this case, necessary conditions for  to be an extremal for
to be an extremal for  in each of the corresponding time intervals excluding the corner points of the function are the Weierstrass-Erdmann corner conditions, which for functions of many variables, can be written as
in each of the corresponding time intervals excluding the corner points of the function are the Weierstrass-Erdmann corner conditions, which for functions of many variables, can be written as
![]()

where  is corner point of
is corner point of  .
.
C.3.4. Constrained Extrema
State-control equations involve finding extrema of functionals of  functions, namely, the state
functions, namely, the state  and controls
and controls  , where only
, where only  of the functions are independent, i.e. the controls
of the functions are independent, i.e. the controls  . For the constrained minimization of functions, two alternative methodologies can be used, namely, the elimination method and the Lagrange multipliers method. The first can be employed if the dependence of variables/functions can be solved with respect to one of them and substituted in the differential
. For the constrained minimization of functions, two alternative methodologies can be used, namely, the elimination method and the Lagrange multipliers method. The first can be employed if the dependence of variables/functions can be solved with respect to one of them and substituted in the differential  .
.
More specifically, assume the problem of finding the extreme values for a function of  variables
variables 
 , given
, given  constraints of the form
constraints of the form
![]()
where only  variables out of the
variables out of the  are independent.
are independent.
Under the elimination method and the above constraints,
![]()
and then by substituting into  , a function
, a function  of
of  independent variables is obtained. Then, this satisfies the following system of equations:
independent variables is obtained. Then, this satisfies the following system of equations:

![]()

which can be solved for  and substituted back in
and substituted back in  to obtain
to obtain 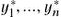 . Then
. Then  can be obtained.
can be obtained.
In the Lagrange multipliers method, the augmented function
![]() (C.23)
(C.23)
is defined and then the differential of the augmented function is obtained

![]()

can be obtained, leading to  .
.
The above are valid for functions of single or multiple variables. In case of minimization of functionals, however, additional constraints in the form of differential equation or point constraints are required, both of which lead to the necessary condition
 (C.24)
(C.24)
where  .
.
Then the general form of the problem is to minimize the functional  and the problem can be eventually solved using either the elimination or the Lagrange multipliers (augmented functional) method.
and the problem can be eventually solved using either the elimination or the Lagrange multipliers (augmented functional) method.
For the case of point constraints, the optimal  is required to satisfy constraints of the form
is required to satisfy constraints of the form  , where only
, where only  out of
out of  components of
components of  are independent. The augmented functional is
are independent. The augmented functional is

On an extremal, the point constraints must be satisfied  , as well as
, as well as  , where
, where

leading to aforementioned condition (C.24).
In the cases when the constraints are given in the form of differential equations  , where again only
, where again only  out of
out of  components of
components of  are independent. In this case, the elimination approach is almost impossible, and Lagrange multipliers have to be adopted. The augmented functional is as before and the conditions on the extremals
are independent. In this case, the elimination approach is almost impossible, and Lagrange multipliers have to be adopted. The augmented functional is as before and the conditions on the extremals  and
and  again yield condition (C.24), where
again yield condition (C.24), where

Finally, the extremal  for the functional could be subject to isoperimetric4 constraints of the form
for the functional could be subject to isoperimetric4 constraints of the form  . In this case, the auxiliary variable
. In this case, the auxiliary variable  is defined, so that in vector form
is defined, so that in vector form  with boundary values
with boundary values  and
and  . In this case, the augmented functional becomes
. In this case, the augmented functional becomes
![]()
Then, the overall system can be solved by using the  available equations obtained from
available equations obtained from

the  equations available from the following:
equations available from the following:

and the  equations available from
equations available from
![]()
while in addition it holds that  .
.
..................Content has been hidden....................
You can't read the all page of ebook, please click here login for view all page.
