7.3. Network-Malware Dynamic Game
7.3.1. Formulation
Following the setup described in Section 7.2, consider a system with two players  (network) and
(network) and  (malware), specified by a system of
(malware), specified by a system of  differential equations [146, P.83]:
differential equations [146, P.83]:  , where
, where  , and
, and  , and the initial condition
, and the initial condition  , and a damage function (the functional)
, and a damage function (the functional)  , where
, where  is the
is the  -dimensional state vector. Player
-dimensional state vector. Player  seeks to minimize
seeks to minimize  by choosing the
by choosing the  dimensional control function
dimensional control function  , and player
, and player  seeks to maximize
seeks to maximize  by choosing the
by choosing the  -dimensional control function
-dimensional control function  . The game is therefore referred to as a dynamic two-player zero-sum game. The players’ payoffs and the set of strategies available to them are called rules of the game. Both players know the rules of the game and each player knows that its opponent knows the rule and ad infinitum.3 As we mentioned in the Introduction to this chapter, we consider open-loop strategies, that is, the controls only depend on time (and not on the state, or the previous history). This is appropriate in the context of the security in networks, as the instantaneous state of the network (exact fraction of the nodes of each type) is impossible (or very costly) to follow, for both of the players.
. The game is therefore referred to as a dynamic two-player zero-sum game. The players’ payoffs and the set of strategies available to them are called rules of the game. Both players know the rules of the game and each player knows that its opponent knows the rule and ad infinitum.3 As we mentioned in the Introduction to this chapter, we consider open-loop strategies, that is, the controls only depend on time (and not on the state, or the previous history). This is appropriate in the context of the security in networks, as the instantaneous state of the network (exact fraction of the nodes of each type) is impossible (or very costly) to follow, for both of the players.
In our context, (7.1) provides the  functions, the initial conditions are provided by (7.1), (7.3) provides the
functions, the initial conditions are provided by (7.1), (7.3) provides the  functions, (7.4a), (7.4b) provide
functions, (7.4a), (7.4b) provide  . Also, we have
. Also, we have  ,
,  . Note that the
. Note that the  functions in our context depend on time
functions in our context depend on time  only implicitly, that is through the state and control functions. Also, the formulation does not capture any other constraints on the state functions, and in our context it does not need to either, owing to Lemma 7.1.
only implicitly, that is through the state and control functions. Also, the formulation does not capture any other constraints on the state functions, and in our context it does not need to either, owing to Lemma 7.1.
We now consider the values of the game. The lower value denoted by  is the overall damage when the minimizing player (
is the overall damage when the minimizing player ( ) is given the upper-hand, i.e. selects its strategy after learning its opponent’s strategy. Mathematically,
) is given the upper-hand, i.e. selects its strategy after learning its opponent’s strategy. Mathematically,  . Conversely, the upper value of the game
. Conversely, the upper value of the game  is defined as
is defined as  Thus,
Thus,  (
( , respectively) is the maximum (minimum, respectively) damage that the malware (network, respectively) can inflict (incur, respectively) if the other player has the upper-hand. Hence,
, respectively) is the maximum (minimum, respectively) damage that the malware (network, respectively) can inflict (incur, respectively) if the other player has the upper-hand. Hence,  . A pair of strategies
. A pair of strategies 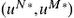 is called a saddle-point if
is called a saddle-point if  for any strategy
for any strategy  of the network and
of the network and  of the malware, and then
of the malware, and then  is the value of the game, and
is the value of the game, and  .
.
Thus, if the network selects its saddle-point strategy  , irrespective of the strategy of the malware, the damage it incurs is at most
, irrespective of the strategy of the malware, the damage it incurs is at most  , which is also the minimum damage that the malware can inflict if it has the upper-hand. Thus, the network’s saddle-point strategy is also its robust strategy, in the sense, that it minimizes the maximum possible damage it can incur. Conversely, the malware’s saddle-point strategy is also its robust strategy, since it maximizes the minimum possible damage it can inflict. Also, the network’s and the malware’s saddle-point strategies are their respective best responses to the other’s robust strategy. We prove the existence of saddle-point pair in the next theorem.
, which is also the minimum damage that the malware can inflict if it has the upper-hand. Thus, the network’s saddle-point strategy is also its robust strategy, in the sense, that it minimizes the maximum possible damage it can incur. Conversely, the malware’s saddle-point strategy is also its robust strategy, since it maximizes the minimum possible damage it can inflict. Also, the network’s and the malware’s saddle-point strategies are their respective best responses to the other’s robust strategy. We prove the existence of saddle-point pair in the next theorem.
7.3.2. A Framework for Computation of the Saddle-point Strategies
Since the set of deterministic strategies of each player is uncountably infinite, the saddle-point strategies and the value of the game cannot be computed using convex or linear programming. We now present a framework for numerical computation of the saddle-point strategies.
Define the Hamiltonian for a given policy pair  in an arbitrary two-person dynamic game as
in an arbitrary two-person dynamic game as  , where the state functions
, where the state functions  are those that correspond to the strategy pair
are those that correspond to the strategy pair  , and
, and 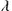 , the costate (or adjoint) functions, are continuous and piecewise differentiable functions of time that satisfy the following system of differential equations wherever the controls
, the costate (or adjoint) functions, are continuous and piecewise differentiable functions of time that satisfy the following system of differential equations wherever the controls  are continuous:
are continuous: 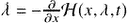 , and the final value (transversality) condition
, and the final value (transversality) condition  . In our context,
. In our context,

where again the state functions  are obtained from (7.1) with
are obtained from (7.1) with  as the control functions, and the costate functions
as the control functions, and the costate functions  are obtained from the following system of differential equations (with
are obtained from the following system of differential equations (with  as the control functions) with the final conditions,
as the control functions) with the final conditions,
![]() (7.5a)
(7.5a)
 (7.5b)
(7.5b)
![]() (7.5c)
(7.5c)
Then, following [146, P.31], a necessary condition for the pair  to be a saddle-point strategy pair is that for all
to be a saddle-point strategy pair is that for all  ,
,
![]() (7.6a)
(7.6a)
![]() (7.6b)
(7.6b)
Henceforth, we denote the saddle-point strategy pair as  , and
, and  ,
,  as the corresponding state and costate functions and
as the corresponding state and costate functions and  as the corresponding Hamiltonian. We now express
as the corresponding Hamiltonian. We now express  in terms of
in terms of  using necessary conditions (7.6). Define
using necessary conditions (7.6). Define  , and
, and  , and
, and  . Now, the Hamiltonian can be written as
. Now, the Hamiltonian can be written as
![]() (7.7)
(7.7)
Thus, the Hamiltonian is a separable function of different components of the defense controls  and the attack control
and the attack control  , that is, each of these appears in different terms in the right-hand side of the above characterization. Now, from the necessary conditions in (7.6) subject to the control constraints in (7.4), the saddle-point strategies are derived as
, that is, each of these appears in different terms in the right-hand side of the above characterization. Now, from the necessary conditions in (7.6) subject to the control constraints in (7.4), the saddle-point strategies are derived as
![]() (7.8)
(7.8)
![]() (7.9)
(7.9)
![]() (7.10)
(7.10)
Since  are uniquely specified once the state and the costate functions are known, the above relations express the saddle-point strategies in terms of the state and costate functions. The strategies
are uniquely specified once the state and the costate functions are known, the above relations express the saddle-point strategies in terms of the state and costate functions. The strategies  can be substituted by the above characterizations in (7.1) and (7.5), resulting in a system of
can be substituted by the above characterizations in (7.1) and (7.5), resulting in a system of  differential equations involving only the state and the costate functions. Using standard numerical methods for solving differential equations, this system can be solved (very fast) using initial and final conditions (7.1) and (7.5). The state and costate functions obtained as solutions will now provide the
differential equations involving only the state and the costate functions. Using standard numerical methods for solving differential equations, this system can be solved (very fast) using initial and final conditions (7.1) and (7.5). The state and costate functions obtained as solutions will now provide the  functions, and thereby the saddle-point strategies via (7.8)–(7.10). The resulting set of differential equations is nonlinear and a closed-form solution is unknown. However, as we will show in the next section, using novel techniques, even without access to the closed-form solution, we can establish the type of behavior that the saddle-point strategies exhibit.
functions, and thereby the saddle-point strategies via (7.8)–(7.10). The resulting set of differential equations is nonlinear and a closed-form solution is unknown. However, as we will show in the next section, using novel techniques, even without access to the closed-form solution, we can establish the type of behavior that the saddle-point strategies exhibit.
7.3.3. Structural Properties of Saddle-point Defense Strategy
We establish that the saddle-point defense strategy has a simple threshold-based structure that ought to facilitate its implementation in a localized manner in resource constrained wireless devices. Specifically, we prove the following.
The overall strategy therefore has the following three phases: In the initial aggressive defense phase, i.e. during  , the susceptibles select the minimum possible reception rate, and the dispatchers transmit the patches whenever they are in contact with any other node. Thus, the quarantining is the most stringent, and the recovery most rapid during this phase. Then, in the interim watchful phase, i.e. during
, the susceptibles select the minimum possible reception rate, and the dispatchers transmit the patches whenever they are in contact with any other node. Thus, the quarantining is the most stringent, and the recovery most rapid during this phase. Then, in the interim watchful phase, i.e. during  , one of the defense controls subsides while the other continues as before. Finally, in the terminal relaxed phase, i.e. in
, one of the defense controls subsides while the other continues as before. Finally, in the terminal relaxed phase, i.e. in  , both defense controls subside, that is, the susceptibles select their normal reception rate and the dispatchers do not transmit the patches. Thus, the QoS in data traffic is back to its normal value and the resource consumption overhead due to patch transmission ends.
, both defense controls subside, that is, the susceptibles select their normal reception rate and the dispatchers do not transmit the patches. Thus, the QoS in data traffic is back to its normal value and the resource consumption overhead due to patch transmission ends.
Note that the defense strategy always chooses either the maximum or the minimum values of the parameters except possibly at  . Such strategies are referred to as bang-bang in the control literature. The durations of the phases (i.e. the values of the threshold times
. Such strategies are referred to as bang-bang in the control literature. The durations of the phases (i.e. the values of the threshold times  ) and which defense subsides in the interim watchful period depend on the damage coefficients
) and which defense subsides in the interim watchful period depend on the damage coefficients  . We will shed more light on the latter in Theorem 7.3 later. But first, we conclude this subsection by proving Theorem 7.2.
. We will shed more light on the latter in Theorem 7.3 later. But first, we conclude this subsection by proving Theorem 7.2.
Strict monotonicity of 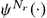
![]()
which after replacement and simplification yields

![]()
Strict monotonicity of 
![]()

In the next theorem, we show that under a sufficient condition, the quarantining period (by reduction of communication rates) ends before the immunization/healing effort is stopped. This is in accordance with our intuition that the primary use of quarantining is buying time for the recovery process in the network.
Note that the condition of the theorem is quite intuitive. For instance, if  , this condition is satisfied when
, this condition is satisfied when  . Recall that the coefficients of the costs were rescaled so that the coefficient of the cost of patching is normalized. Thus, this means when the instantaneous cost of per unit reduction of commutation rates (quarantining) is no less than per unit patching. The other parameters in
. Recall that the coefficients of the costs were rescaled so that the coefficient of the cost of patching is normalized. Thus, this means when the instantaneous cost of per unit reduction of commutation rates (quarantining) is no less than per unit patching. The other parameters in  refer to the cases of relatively small initial susceptible pool, and a relatively fast healing rate.
refer to the cases of relatively small initial susceptible pool, and a relatively fast healing rate.
Note that the case of  occurs when
occurs when  does not have a zero-crossing point and is hence non-negative throughout
does not have a zero-crossing point and is hence non-negative throughout  . In this case, the immunization/healing effort is never launched.
. In this case, the immunization/healing effort is never launched.
7.3.4. Structure of the Saddle-point Attack Strategy
The saddle-point attack has a simple first-amass, then slaughter structure in the special case that the worm benefits from killing only through the final tally of the dead (i.e.  ), and the patches can only immunize the susceptibles, but cannot heal the infectives (i.e.
), and the patches can only immunize the susceptibles, but cannot heal the infectives (i.e.  ). Specifically, we have the following.
). Specifically, we have the following.
Thus, the worm does not kill any infective during the initial amass period of  when it uses them to spread the infection; it slaughters them at the maximum rate subsequently. The intuition behind this structure is as follows. Once the worm infects a host, it never loses it to the recovery process, and thus, since it benefits from killing a host only because this enhances the final tally of the dead, it ought to kill hosts toward the end and utilize them before. The proof follows.
when it uses them to spread the infection; it slaughters them at the maximum rate subsequently. The intuition behind this structure is as follows. Once the worm infects a host, it never loses it to the recovery process, and thus, since it benefits from killing a host only because this enhances the final tally of the dead, it ought to kill hosts toward the end and utilize them before. The proof follows.
The saddle-point attack strategy may however be more involved when either  or
or  . For example, Fig. 7.2 depicts the saddle-point strategies and the state evolution in an example scenario where
. For example, Fig. 7.2 depicts the saddle-point strategies and the state evolution in an example scenario where 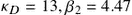 . The malware starts killing the nodes from the beginning, but then it stops the killing and infects the newly accessible susceptible nodes, boosting the fraction of the infective and toward the end, starts to kill them all again.
. The malware starts killing the nodes from the beginning, but then it stops the killing and infects the newly accessible susceptible nodes, boosting the fraction of the infective and toward the end, starts to kill them all again.

FIGURE 7.2 State evolution and saddle-point strategies. The parameters of the game are as follows:  ,
, ,
, ,
, ,
, ,
, ,
, , and initial fractions
, and initial fractions  ,
, ,
, , and
, and  . From© 2012 IEEE. Reprinted, with permission, from Khouzani MHR, Sarkar S, Altman E. Saddle-point strategies in malware attack. IEEE J Sel Areas Commun 2012;30(1):31–43.
. From© 2012 IEEE. Reprinted, with permission, from Khouzani MHR, Sarkar S, Altman E. Saddle-point strategies in malware attack. IEEE J Sel Areas Commun 2012;30(1):31–43.
 ,
, ,
, ,
, ,
, ,
, ,
, , and initial fractions
, and initial fractions  ,
, ,
, , and
, and  . From© 2012 IEEE. Reprinted, with permission, from Khouzani MHR, Sarkar S, Altman E. Saddle-point strategies in malware attack. IEEE J Sel Areas Commun 2012;30(1):31–43.
. From© 2012 IEEE. Reprinted, with permission, from Khouzani MHR, Sarkar S, Altman E. Saddle-point strategies in malware attack. IEEE J Sel Areas Commun 2012;30(1):31–43...................Content has been hidden....................
You can't read the all page of ebook, please click here login for view all page.


