6.3. Worm’s Optimal Control
Let ((S,I,D),ν)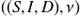 be an optimal solution. Let the Hamiltonian H
be an optimal solution. Let the Hamiltonian H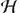 , and costate or adjoint functions λS(t)
, and costate or adjoint functions λS(t)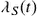 , λI(t)
, λI(t) , and λD(t)
, and λD(t) , and a scalar λ0≥0
, and a scalar λ0≥0 be defined as the following:
be defined as the following:
H:=λ0f(I)+(λI−λS)βIS−λSQ(S,I)S−λIB(S,I)I+(λD−λI)νI,
![]() (6.4)
(6.4)
˙λS=−∂H∂S=−(λI−λS)βI+λSQ(S,I)+λSQS(S,I)S,˙λI=−∂H∂I=−λ0f′−(λI−λS)βS+λIB(S,I)+λIBI(S,I)I−(λD−λI)ν,˙λD=−∂H∂D=0
 (6.5)
(6.5)
along with the transversality (final) conditions,
λS(T)=0,λI(T)=0,λD(T)=λ0κ.
![]() (6.6a)
(6.6a)
Then according to Pontryagin’s maximum principle with terminal constraints— [70, P.111 theorem 3.14] —there exist continuous and piecewise continuously differentiable costate functions λS , λI
, λI , and λD
, and λD , and a constant λ0≥0
, and a constant λ0≥0 that at every point t∈[0…T]
that at every point t∈[0…T] where ν(⋅)
where ν(⋅) is continuous, satisfy (6.5) and transversality conditions (6.6), and we have
is continuous, satisfy (6.5) and transversality conditions (6.6), and we have
→λ≢
![]() (6.7a)
(6.7a)
![]() (6.7b)
(6.7b)
First, we argue that  has to be strictly positive. This is because if
has to be strictly positive. This is because if  , then the system of ODE in (6.5) becomes a homogeneous ODE with the final conditions of
, then the system of ODE in (6.5) becomes a homogeneous ODE with the final conditions of  . However, this ODE has the unique solution of
. However, this ODE has the unique solution of  , which contradicts (6.7a). Hence, combined with the property that
, which contradicts (6.7a). Hence, combined with the property that  , we have
, we have  .
.
Define the switching function  as follows:
as follows:
![]() (6.8)
(6.8)
which is a continuous and piecewise continuously differential function of time and referring to (6.6) has the following final value:
![]() (6.9)
(6.9)
The positivity comes from the facts  ,
,  , and
, and  according to Lemma 6.1. Introduction of
according to Lemma 6.1. Introduction of  allows us to rewrite the Hamiltonian in (6.4) as follows:
allows us to rewrite the Hamiltonian in (6.4) as follows:
![]() (6.10)
(6.10)
According to PMP in (6.7b), we have
![]() (6.11)
(6.11)
Hence, the optimal  satisfies
satisfies  , for all
, for all  . Thus, to find the optimal controller, one needs to maximize the linear function
. Thus, to find the optimal controller, one needs to maximize the linear function  over the admissible set
over the admissible set  , which yields
, which yields
![]() (6.12)
(6.12)
hence the name switching function. An immediate observation of the above relation is the following important property:
![]() (6.13)
(6.13)
Also note that according to (6.9),  and thus by continuity of
and thus by continuity of  and following (6.12),
and following (6.12),  over an interval of nonzero length toward the end of
over an interval of nonzero length toward the end of  interval which extends until time
interval which extends until time  .
.
6.3.1. Structure of the Maximum Damage Attack
Whether in practice the worm can indeed inflict the maximum damages developed in this section depends on implementability of the optimal strategies. Specifically, if the optimal policies that inflict the maximum damage are complex to execute, then the worm may not be able to perform them since they are limited by the capabilities of their resource constrained hosts as well. Inauspiciously though, we show that optimal attack strategies follow simple structures (Theorem 6.1) which make them conducive to implementation. Fig. 6.2 provides visualization of the theorem. Note that in the left figure, the patching only immunizes the susceptible nodes ( but
but  ), while in the right figure, patching can equally immunize the susceptible and clean and immunize the infective nodes (
), while in the right figure, patching can equally immunize the susceptible and clean and immunize the infective nodes ( ).
).

FIGURE 6.2 Evaluation of the optimal controller and the corresponding states as functions of time. The parameters are time horizon:  , initial infection fraction:
, initial infection fraction:  , contact rate:
, contact rate:  , instantaneous reward rate of infection for the malware:
, instantaneous reward rate of infection for the malware:  , reward per each killed node:
, reward per each killed node:  . Also, we have taken
. Also, we have taken  , and
, and  in the left and
in the left and  in the right figures. That is, in the left figure, patches can only immunize the susceptible nodes but in the right figure, the same patch can successfully remove the infection, if any, and immunize the node against future infection. We can see that when patching can recover the infective nodes too (right figure), then the malware starts the killing phase earlier. This makes sense as deferring the killing in the hope of finding a new susceptible is now much riskier.
in the right figures. That is, in the left figure, patches can only immunize the susceptible nodes but in the right figure, the same patch can successfully remove the infection, if any, and immunize the node against future infection. We can see that when patching can recover the infective nodes too (right figure), then the malware starts the killing phase earlier. This makes sense as deferring the killing in the hope of finding a new susceptible is now much riskier.
 , initial infection fraction:
, initial infection fraction:  , contact rate:
, contact rate:  , instantaneous reward rate of infection for the malware:
, instantaneous reward rate of infection for the malware:  , reward per each killed node:
, reward per each killed node:  . Also, we have taken
. Also, we have taken  , and
, and  in the left and
in the left and  in the right figures. That is, in the left figure, patches can only immunize the susceptible nodes but in the right figure, the same patch can successfully remove the infection, if any, and immunize the node against future infection. We can see that when patching can recover the infective nodes too (right figure), then the malware starts the killing phase earlier. This makes sense as deferring the killing in the hope of finding a new susceptible is now much riskier.
in the right figures. That is, in the left figure, patches can only immunize the susceptible nodes but in the right figure, the same patch can successfully remove the infection, if any, and immunize the node against future infection. We can see that when patching can recover the infective nodes too (right figure), then the malware starts the killing phase earlier. This makes sense as deferring the killing in the hope of finding a new susceptible is now much riskier.Recall that one of the basic tradeoff/s decisions that the attacker was dynamically faced with was the best timing to kill an infective node. Specifically, should an attacker kill a node as soon as it is infected so as to have claimed a casualty and secured a large damage on the network but losing the chance to further the spread? Or should it wait in anticipation of contacting new susceptible nodes and extend the contagion but at the risk of being detected and removed by the defender before it gets to destroy the host. Is the tradeoff broken by choosing an intermediate probability of killing the host? Theorem 6.1 states not.
In words, an optimal  is of bang-bang form, that is, it possesses only two possible values
is of bang-bang form, that is, it possesses only two possible values 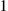 and
and  , and switches abruptly between them. It has at most one such jump, which necessarily culminates at
, and switches abruptly between them. It has at most one such jump, which necessarily culminates at 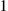 . Thus, the theorem says that although killing a node early on would ensure a partial damage, the overall damage is more if this decision is deferred until toward the end of the attacking period despite the risk of recovery of the infective nodes by the system. Specifically, at the start of the outbreak, the number of susceptible nodes is high and infective nodes can be used to further propagate the infection. As time passes by, the level of susceptible nodes drops due to both spread of infection and immunization effort by the system. At a certain threshold, the risk of recovery of the infective nodes in the remaining time outweighs the potential benefit by spreading the infection. At this point, whose exact value depends on the parameters of the case, the malware starts killing the nodes with maximum possible rate. This will ensure that infective nodes are maximally used for spread of the infection and for attacker’s malicious activities.
. Thus, the theorem says that although killing a node early on would ensure a partial damage, the overall damage is more if this decision is deferred until toward the end of the attacking period despite the risk of recovery of the infective nodes by the system. Specifically, at the start of the outbreak, the number of susceptible nodes is high and infective nodes can be used to further propagate the infection. As time passes by, the level of susceptible nodes drops due to both spread of infection and immunization effort by the system. At a certain threshold, the risk of recovery of the infective nodes in the remaining time outweighs the potential benefit by spreading the infection. At this point, whose exact value depends on the parameters of the case, the malware starts killing the nodes with maximum possible rate. This will ensure that infective nodes are maximally used for spread of the infection and for attacker’s malicious activities.
In summary, Theorem 6.1 provides the optimal attack as follows: initially, the effort of the malware is focused on spreading the worm and amassing infective nodes without killing any. Subsequently, the reverse course of action is taken: at a threshold time, the amassed infected nodes are slaughtered at the highest rate which lasts till the end of the interval.
Note that the optimal killing policy ( ) will be completely specified by the (only possible) jump points (trigger epoch). Given the flexibility provided by software-driven devices, the infective nodes can subsequently execute these strategies without coordinating any further among themselves or with any central entity. The transition time can be determined by solving a system of differential equations, as described in the previous sections. Such systems can be solved very fast due to the existence of efficient numerical algorithms for solving differential equations, and the computation time is constant in that it does not depend on the number of nodes
) will be completely specified by the (only possible) jump points (trigger epoch). Given the flexibility provided by software-driven devices, the infective nodes can subsequently execute these strategies without coordinating any further among themselves or with any central entity. The transition time can be determined by solving a system of differential equations, as described in the previous sections. Such systems can be solved very fast due to the existence of efficient numerical algorithms for solving differential equations, and the computation time is constant in that it does not depend on the number of nodes  . Note also that our algorithms do not require any local or global information as time progresses and only the initial information is sufficient to determine the decision of infective nodes for the entire interval.
. Note also that our algorithms do not require any local or global information as time progresses and only the initial information is sufficient to determine the decision of infective nodes for the entire interval.
Fig. 6.3 shows the effect of increasing the patching rates  and
and  on the trigger epoch. We observe that increasing the patching rate generally decreases the jump time. Intuitively, in a system with a large recovery rate, both the susceptible and infective nodes recover rapidly. Hence, the worm should start killing them earlier in order to not lose too many nodes in the competition with the network administrator to the pool of recovered. Note also that the starting time of the killing is sensitive to the value of recovery rate when the patching can impact both infective as well as susceptible nodes (
on the trigger epoch. We observe that increasing the patching rate generally decreases the jump time. Intuitively, in a system with a large recovery rate, both the susceptible and infective nodes recover rapidly. Hence, the worm should start killing them earlier in order to not lose too many nodes in the competition with the network administrator to the pool of recovered. Note also that the starting time of the killing is sensitive to the value of recovery rate when the patching can impact both infective as well as susceptible nodes ( ). This is because when
). This is because when  , once a node is infected, then it will not be recovered by the system and is safely in the tally of the worm, but when
, once a node is infected, then it will not be recovered by the system and is safely in the tally of the worm, but when  , the worm is in competition with the system and excessively deferring the killing is ever more risky if the speed of recovery of the victims is increased.
, the worm is in competition with the system and excessively deferring the killing is ever more risky if the speed of recovery of the victims is increased.

FIGURE 6.3 The jump (up) point of optimal  , i.e. the starting time of the slaughter period, for different values of the patching and rates. For both curves, we have taken the recovery rate of the susceptible nodes, i.e.
, i.e. the starting time of the slaughter period, for different values of the patching and rates. For both curves, we have taken the recovery rate of the susceptible nodes, i.e.  as
as  , and the recovery rate of the infective nodes, i.e.
, and the recovery rate of the infective nodes, i.e.  , once as zero and once as the same as
, once as zero and once as the same as  where
where  is varied from
is varied from 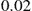 to
to  with steps of
with steps of 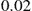 . The rest of the parameters are
. The rest of the parameters are  ,
,  ,
,  ,
,  , and
, and  . Note that when
. Note that when  , then for
, then for  , the malware starts killing the infective nodes from time zero.
, the malware starts killing the infective nodes from time zero.
 , i.e. the starting time of the slaughter period, for different values of the patching and rates. For both curves, we have taken the recovery rate of the susceptible nodes, i.e.
, i.e. the starting time of the slaughter period, for different values of the patching and rates. For both curves, we have taken the recovery rate of the susceptible nodes, i.e.  as
as  , and the recovery rate of the infective nodes, i.e.
, and the recovery rate of the infective nodes, i.e.  , once as zero and once as the same as
, once as zero and once as the same as  where
where  is varied from
is varied from 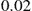 to
to  with steps of
with steps of 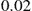 . The rest of the parameters are
. The rest of the parameters are  ,
,  ,
,  ,
,  , and
, and  . Note that when
. Note that when  , then for
, then for  , the malware starts killing the infective nodes from time zero.
, the malware starts killing the infective nodes from time zero.In the next section, we provide the proof of the theorem.
6.3.2. Proof of Theorem 6.1
We first obtain some useful properties of the Hamiltonian and system states. The second observation is that  satisfies the following condition:
satisfies the following condition:
We will also use the following key lemma in the sequel.
We are now ready to proceed to the proof of the theorem.
6.3.3. Proof of Theorem 6.1: Optimal Rate of Killing
..................Content has been hidden....................
You can't read the all page of ebook, please click here login for view all page.


