We now have an autoencoder that takes in a credit card transaction and outputs a credit card transaction that looks more or less the same. However, this is not why we built the autoencoder. The main advantage of an autoencoder is that we can now encode the transaction into a lower dimensional representation that captures the main elements of the transaction.
To create the encoder model, all we have to do is to define a new Keras model that maps from the input to the encoded state:
encoder = Model(data_in,encoded)
Note that you don't need to train this model again. The layers keep the weights from the previously trained autoencoder.
To encode our data, we now use the encoder model:
enc = encoder.predict(X_test)
But how would we know whether these encodings contain any meaningful information about fraud? Once again, visual representation is key. While our encodings have fewer dimensions than the input data, they still have 12 dimensions. It's impossible for humans to think about a 12-dimensional space, so we need to draw our encodings in a lower dimensional space while still preserving the characteristics we care about.
In our case, the characteristic we care about is proximity. We want points that are close to each other in the 12-dimensional space to be close to each other in the 2-dimensional plot. More precisely, we care about the neighborhood. We want the points that are closest to each other in the high-dimensional space to also be closest to each other in the low-dimensional space.
Preserving the neighborhood is important because we want to find clusters of fraud. If we find that fraudulent transactions form a cluster in our high-dimensional encodings, then we can use a simple check if a new transaction falls into the fraud cluster to flag a transaction as fraudulent. A popular method to project high-dimensional data into low-dimensional plots while preserving neighborhoods is called t-distributed stochastic neighbor embedding, or t-SNE.
In a nutshell, t-SNE aims to faithfully represent the probability that two points are neighbors in a random sample of all points. That is, it tries to find a low-dimensional representation of data in which points in a random sample have the same probability of being the closest neighbors as in the high-dimensional data:

How t-SNE measures similarity
The t-SNE algorithm follows these steps:
- Calculate the Gaussian similarity between all points. This is done by calculating the Euclidean (spatial) distance between points and then calculating the value of a Gaussian curve at that distance, as you can see in the preceding diagram. The Gaussian similarity for all points, j, from point i can be calculated as follows:

In the preceding formula,
 2 is the variance of the Gaussian distribution. We will look at how to determine this variance later on in this chapter. Note that since the similarity between points i and j is scaled by the sum of distances between i and all other points (expressed as k), the similarity between i and j,
2 is the variance of the Gaussian distribution. We will look at how to determine this variance later on in this chapter. Note that since the similarity between points i and j is scaled by the sum of distances between i and all other points (expressed as k), the similarity between i and j,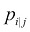 , can be different from the similarity between j and i,
, can be different from the similarity between j and i,  . Therefore, we average the two similarities to gain the final similarity that we'll work with going forward:
. Therefore, we average the two similarities to gain the final similarity that we'll work with going forward:
In the preceding formula, n is the number of data points.
- Randomly position the data points in the lower dimensional space.
- Calculate the t-similarity between all the points in the lower dimensional space:

- Just like in training neural networks, we will optimize the positions of the data points in the lower dimensional space by following the gradient of a loss function. The loss function, in this case, is the Kullback–Leibler (KL) divergence between the similarities in the higher and lower dimensional space. We will give the KL divergence a closer look in the section on variational autoencoders. For now, just think of it as a way to measure the difference between two distributions. The derivative of the loss function with respect to the position yi of data point i in the lower dimensional space is as follows:

- Adjust the data points in the lower dimensional space by using gradient descent, moving points that were close in the high-dimensional data closer together and moving points that were further away further from each other:

- You will recognize this as a form of gradient descent with momentum, as the previous gradient is incorporated into the updated position.
The t-distribution used always has one degree of freedom. This freedom leads to a simpler formula as well as some nice numerical properties that lead to faster computation and more useful charts.
The standard deviation of the Gaussian distribution can be influenced by the user with a perplexity hyperparameter. Perplexity can be interpreted as the number of neighbors we expect a point to have. A low perplexity value emphasizes local proximities, while a high perplexity value emphasizes global perplexity values. Mathematically, perplexity can be calculated as follows:

Here Pi is a probability distribution over the position of all data points in the dataset and ![]() is the Shanon entropy of this distribution, calculated as follows:
is the Shanon entropy of this distribution, calculated as follows:

While the details of this formula are not very relevant to using t-SNE, it is important to know that t-SNE performs a search over values of the standard deviation, ![]() , so that it finds a global distribution, Pi, for which the entropy over our data is of our desired perplexity. In other words, you need to specify the perplexity by hand, but what that perplexity means for your dataset also depends on the dataset itself.
, so that it finds a global distribution, Pi, for which the entropy over our data is of our desired perplexity. In other words, you need to specify the perplexity by hand, but what that perplexity means for your dataset also depends on the dataset itself.
Laurens Van Maarten and Geoffrey Hinton, the inventors of t-SNE, report that the algorithm is relatively robust for choices of perplexity between 5 and 50. The default value in most libraries is 30, which is a fine value for most datasets. However, if you find that your visualizations are not satisfactory, then tuning the perplexity value is probably the first thing you would want to do.
For all the math involved, using t-SNE is surprisingly simple. Scikit-learn has a handy t-SNE implementation that we can use just like any algorithm in scikit-learn.
We first import the TSNE class, and then we can create a new TSNE instance. We define that we want to train for 5000 epochs, and use the default perplexity of 30 and the default learning rate of 200. We also specify that we would like output during the training process. We then call fit_transform, which transforms our 12 encodings into 2-dimensional projections:
from sklearn.manifold import TSNE tsne = TSNE(verbose=1,n_iter=5000) res = tsne.fit_transform(enc)
As a word of warning, t-SNE is quite slow as it needs to compute the distances between all the points. By default, scikit-learn uses a faster version of t-SNE called the Barnes Hut approximation. While it's not as precise, it's significantly faster.
There's also a faster Python implementation of t-SNE that can be used as a drop-in replacement of the scikit-learn implementation. However, this is not as well documented and contains fewer features, therefore we will not be covering it in this book.
Note
Note: You can find the faster implementation with installation instructions under the following URL https://github.com/DmitryUlyanov/Multicore-TSNE.
We can then plot our t-SNE results as a scatterplot. For illustration, we will distinguish frauds from non-frauds by color, with frauds being plotted in red and non-frauds being plotted in blue. Since the actual values of t-SNE do not matter as much, we will hide the axes:
fig = plt.figure(figsize=(10,7)) scatter =plt.scatter(res[:,0],res[:,1],c=y_test, cmap='coolwarm', s=0.6) scatter.axes.get_xaxis().set_visible(False) scatter.axes.get_yaxis().set_visible(False)
Let's now see, what the output chart will look like:

t-SNE results in the form of a scatter graph
For easier spotting, and for those reading the print version, the cluster containing the most frauds, those that are marked red, has been marked with a circle. You can see that the frauds are nicely separate from the rest of the genuine transactions, those in blue. Clearly, our autoencoder has found a way to distinguish frauds from the genuine transaction without being given labels. This is a form of unsupervised learning.
In fact, plain autoencoders perform an approximation of PCA, which is useful for unsupervised learning. In the output chart, you can see that there are a few more clusters that are clearly separate from the other transactions, yet these are not frauds. Using autoencoders and unsupervised learning, it is possible to separate and group our data in ways that we did not even think of before. For example, we might be able to cluster transactions by purchase type.
Using our autoencoder, we could now use the encoded information as features for a classifier. However, what's even better is that with only a slight modification of the autoencoder, we can generate more data that has the underlying properties of a fraud case while having different features. This is done with a variational autoencoder, which will be the focus of the next section.
