Appendix B: Advanced Dynamic System Control Techniques
As stated in the introduction, the hybrid vehicle system is a complex electromechanical system, and many control problems are fundamentally multivariable interacting with many actuators, performance variables, and sensors; furthermore, they are generally nonlinear, exhibit fast parameter variation, and operate under uncertain and changing conditions. In addition, many control design objectives are very difficult to formalize, and many variables that are of great concern are not measurable.
Control theory and methodologies have substantially advanced since the 1950s. Pontryagin's maximum principle, Bellman's dynamic programming, and Kalman filtering set up the foundation of modern control theory, and the theories of controllability, observability and feedback stabilization of linear state space models are the breakthroughs of the modern multivariable feedback control methodologies. Nowadays, a multifaceted but coherent body of control theory and methodology has been forming and is playing crucial roles in industrialized societies.
Typically, even a small improvement in the control algorithm can yield system performance enhancement significantly. Advanced control theory and methodologies are providing new opportunities for hybrid vehicle systems from improvement of dynamic performances to enhancement of passenger safety level and achievement of superior fuel economy. This chapter will briefly introduce some advanced control methodologies, including optimal control, adaptive control, model predictive control, robust control, and fault-tolerant control for hybrid vehicle applications.
B.1 pole placement of control system
Pole location regulation is one of the first applications of the state space approach. The problem of pole placement is to move the poles of a given linear system to the specific locations in the s plane by means of state feedback. The pole placement technique provides a method by which engineers can design a linear feedback controller that adjusts the system parameters so that the closed-loop system has the desired response characteristics. The design problem is formulated as follows.
Given the system described in state space form as
where u is the control variable, y is the measured output variable, and x is the state variable, the corresponding transfer function is
B.2 ![]()
The design objective is to find the following admissible feedback control law such that the closed-loop system has a desired set of poles:
B.3 ![]()
where r is the reference input and K is the feedback gain vector. The corresponding closed-loop system state space equation and transfer function are
B.4 ![]()
B.5 ![]()
The condition that the poles of system (B.5) can be placed in any desired location is that the system must be controllable. As stated in Appendix A, if a system is controllable, the composite matrix ![]() must be of rank n; furthermore, if system (B.1) is controllable, there exists a nonsingular transformation matrix T that transforms equation (B.1) to the phase-variable canonical form. Huo (1982) gave the transformation matrix
must be of rank n; furthermore, if system (B.1) is controllable, there exists a nonsingular transformation matrix T that transforms equation (B.1) to the phase-variable canonical form. Huo (1982) gave the transformation matrix
B.6 
where
B.7 ![]()
The transformed phase-variable canonical form is
B.8 
where ai, i = 0, … , n − 1, are coefficients of the characteristic equation
B.9 ![]()
If we assume the state feedback is given by (B.3) as
B.10 ![]()
the states of the closed-loop control system can be expressed as
If the poles of the closed-loop system are placed on the desired locations ![]() , then the desired characteristic equation is
, then the desired characteristic equation is
B.12 ![]()
Thus, the required feedback gains k1, k2, … , kn can be determined from the equations
In general, the following steps need to be taken to apply the pole placement technique to the system described by state space equation (B.1):
B.14 ![]()
B.15 ![]()
B.16 ![]()
B.17 
B.18 ![]()
B.19 ![]()
that is,
![]()
B.20 
The characteristic equation and controllability matrix are
B.21 ![]()
B.22 
The transformation matrix T and transformed matrix Ac, Bc, Cc are
B.23 
B.24 
If we intend to find the feedback gain for the system such that the poles of the closed-loop system are located at − 1, − 2, and − 3, the characteristic equation of the closed-loop system can be obtained as
B.25 ![]()
From equation (B.13) and (B.17), we have
B.26 
The closed-loop control system state and output equations in the transformed coordinates are
B.27 
In the original coordinates, the feedback gains can be obtained from
B.28 
Finally, the closed-loop control system is achieved in the original coordinates:
B.29 
B.2 Optimal control
The fundamental control objective of a hybrid vehicle system is to maximize fuel economy and minimize emissions subjected to the drivability and safety requirements under various driving scenarios. Different from optimization, the optimal control is to find a control law for a given dynamic system such that a certain optimum objective is achieved with physical constraints satisfied at the same time. This section will introduce the basic principle of optimal control design, outline brief design procedures, and illustrate results with simple examples.
Figure B.1 Open-loop control system.

Figure B.2 Closed-loop control system.

B.2.1 Optimal Control Problem Formulation
The optimal control problem is formulated as follows.
B.30 ![]()
where x = [x1 x2 ![]() xn]T is the state vector and u = [u1 u2
xn]T is the state vector and u = [u1 u2 ![]() um]T is the control vector.
um]T is the control vector.
B.31 ![]()
The region where all control variables satisfy the constraints is called the admissible control region.
B.32 ![]()
B.33 ![]()
This form will lead to a suitable mathematical treatment of qualitative consideration penalizing both large deviations from the desired state and increased control actions more severely.
B.2.2 Pontryagin's Maximum Method
Pontryagin presented his maximum principle to solve the optimal control problem in 1962 (Pontryagin et al., 1962). The basic design procedure with an example is given in this section.
For a given system
B.34 ![]()
if the objective function and Hamilton function are defined as
B.35 
the optimal control u*(t), which drives the system from initial states x(ti) to end states x(tf) with the maximum J, can be found based on the following steps extracted from Pontryagin's maximum principle:
B.36 ![]()
B.37 ![]()
B.38 ![]()
where U is the admissible region of control variable u(t).
B.39 ![]()
The objective function is defined as
B.40 ![]()
and the admissible control region is
B.41 ![]()
The optimal control action u*(t) can be found by the following steps:
B.42 ![]()
B.43 ![]()
B.44 
B.45 ![]()
B.2.3 Dynamic Programming
The fundamental principle of the dynamic programming method is based on Bellman's principle of optimality, which states that an optimal policy has the property that whatever the initial state and the initial decision the remaining decision must form an optimal policy with regard to the state resulting from the first decision (Bellman, 1957). Bellman's principle of optimality immediately leads to the following computation algorithm to find the optimal control law.
Consider a discrete system described by the difference equation
The objective function is
B.47 
The dynamic programming method is to find the sequence of decision u(0), u(1), … , u(N − 1) which maximizes the objective function (B.47). The dynamic programming can be used either backward or forward. Backward programming is the normal method which starts from the final point to the initial point where x(0) is specified to x0, and the sequence of optimal controls u(N − 1), u(N − 2), … , u(0) is thus generated. A set of recursive relationships is provided which enables establishment of the sequence J(x(N − 1), 1), J(x(N − 2), 2), … , J(x(0), N) and the optimal control sequence u*(N − 1), u*(N − 2), … , u*(0).
At present, if the final state x(N) is specified as x(N) = xf, the final state needs not be included in the summation of the objective function (B.47), and this is the fixed end condition problem. In practice, an optimal decision is made through the following procedure:
B.48 ![]()
Based on the system state equation (B.46), the final state x(N) = xf is reached from the previous state x(N − 1) driven by optimal control u*(N – 1), that is,
B.49 ![]()
B.50 ![]()
where the notation J*(x(2), N − 2) signifies the objective function evaluated over N − 1 times and the end state xf is reached by the optimal control sequence u*(N − 1), u*(N − 2), … , u*(2).
B.51 ![]()
The dynamic programming method is an important optimal control technique to improve hybrid vehicle fuel economy and other performance. Many HEV control problems such as energy management can be treated as an optimal control problem and solved by dynamic programming. The following two examples are given to help readers understand the principle of dynamic programming and two detailed engineering examples are presented in Chapters 6 and 8.
Figure B.3 Dynamic programming method.

B.52 
Find the optimal control u which makes the objective J be minimum based on the principle of dynamic programming.
B.53 ![]()
B.54 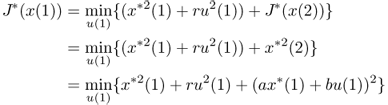
B.55 
B.56 ![]()
B.57 
B.58 
B.2.4 Linear Quadratic Control
Linear quadratic control (LQC), another important optimal problem, assumes that the system is linear and the objective function has the quadratic form
where Q is symmetric positive semidefinite, R and S are symmetric positive definite, and they are normally chosen as diagonal matrices.
Based on Pontryagin's maximum principle, the optimal LQC problem can be solved through the following steps:
B.60 ![]()
Then the system state and costate can be described by
B.61 
with the specified initial conditions x(t0) = x0 and boundary conditions ![]()
B.67 ![]()
This equation is called a matrix Riccati equation, which is a nonlinear differential equation. Once P is solved, the feedback control law is formed. The optimal feedback system may be represented by the diagram shown in Fig. B.4.
B.68 ![]()
where P is symmetric positive matrix.
B.69 
Find the optimal feedback control law that has the objective function J minimized.
![]()
From the following controllability matrix, we know that the given system is controllable:
B.70 ![]()
From equation (B.64), the optimal feedback control law is
B.71 ![]()
where p12 and p22 are the solutions of the Riccati equation
B.72 
Equating the above matrix, we obtain the three equations
B.73 ![]()
Solving the equations, we obtain
B.74 ![]()
Since the matrix P has to be symmetric positive definite, the solutions are determined as
![]()
Thus, the optimal control law is
B.75 ![]()
If we assume that the system output is x2, the closed-loop control system is
B.76 
The diagram of the closed-loop system is shown in Fig. B.5a. The transfer function and the pole locations are described by the equation
B.77 ![]()
If we take parameter a as the changeable variable, we can get the root locus of the optimal feedback system, and the root locus diagram is shown in Fig. B.5b.
Figure B.4 Optimal LQC feedback control system.

Figure B.5 Obtained optimal feedback system.

B.3 Stochastic and adaptive control
So far, the presented control methods are for systems where the dynamics are known and equations have been established. However, a hybrid vehicle system normally operates in a dynamic environment of different road, weather, and load conditions. It would be impractical to build an exact mathematical model to describe the dynamics of a hybrid vehicle system. To have the vehicle model meet performance requirements in the presence of uncertainties and disturbances, the developed control algorithms must be robust with respect to such uncertainties and even be able to adapt to the slow dynamic changes of the system. This section briefly introduces the common control techniques dealing with such uncertainties.
B.3.1 Minimum-Variance Prediction and Control
B.3.1.1 Minimum-Variance Prediction
Consider a single-input, single-output linear system described by the ARMAX model
where
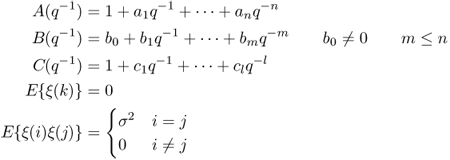
and {ξ(k)} is an uncorrelated random variable with zero mean and standard deviation σ. It is also assumed that all the zeros of the polynomial C(q−1) are inside the unit disc.
Now the problem is to predict y(k + d) based on the observed input and output variables u(k), u(k − 1), … , y(k), y(k − 1), … at time k in the presence of measurement noise. It can be proved that the optimal (minimum-variance) prediction of y(k + d) can be achieved by the following equation (Åstrom and Witternmark, 1984).
Let us rewrite equation (B.78) as
B.79 ![]()
that is,
The last term of the equation can be expressed as
B.81 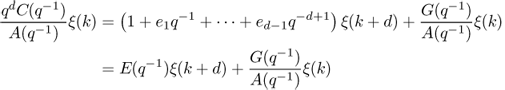
where the polynomials E(q−1) and G(q−1) are the quotient and remainder of dividing qdC(q−1)/[A(q−1)].
Thus, equation (B.80) is of the form
B.82 ![]()
Equation (B.78) can also be rewritten as
Substituting equation (B.83) into (B.82), we have
B.84 
If we let ![]() (k + d) be the prediction of y(k + d), then the minimum-variance prediction of y(k + d) will be
(k + d) be the prediction of y(k + d), then the minimum-variance prediction of y(k + d) will be
Since the observed input and output data u(k), u(k − 1), … , y(k), y(k − 1), … are independent with the further noise sequence ξ(k + 1), ξ(k + 2), … , ξ(k + d), equation (B.85) is equal to
Since the first term of equation (B.86) is not predictable, the second term must be zero for J to be a minimum.
Therefore, the minimum-variance prediction of y(k + d) is
B.87 ![]()
and the variance of the optimal prediction error is
B.88 ![]()
where
B.89 
B.90 ![]()
where parameters a1 = − 0.9, b0 = 0.5, c1 = 0.7, and {ξ(k)} are independent random variables. Determine the minimum-variance prediction and the variance of the prediction error over two steps, that is, ![]() *(k + 2|k).
*(k + 2|k).
B.91 ![]()
Based on the above polynomials, we can assume the equations
B.92 ![]()
Solving the following Diophantine equation, we can obtain the quotient and remainder as
B.93 
Equating the coefficients of (B.92) and (B.93), we have
B.94 ![]()
Thus, the minimum-variance prediction and the variance of the prediction error are
B.95 
Taking parameters a1 = − 0.9, b0 = 0.5, c1 = 0.7 into the (B.94), we get e1 = − 1.6, g0 = 1.44, f0 = 0.5, and f1 = 0.8. The variance of solved prediction error ![]() .
.
B.3.1.2 Minimum-Variance Control
To derive the minimum-variance control law, we assume that system (B.78) is a minimum-phase system where all zeros are located inside the unit disc. The objective of minimum-variance control is to determine a control law which has the following minimum objective function:
B.96 ![]()
Based on minimum-variance prediction, system (B.78) can be expressed as
B.97 ![]()
Substituting (B.97) into the objective function (B.96), we have
Since the term E(q−1)ξ(k + d) = ξ(k) + e1ξ(k + 1) + ![]() + ed−1ξ(k + d) in the equation is a random sequence and independent with observed input and output data at time k, k − 1, k − 2, … , equation (B.98) is equal to
+ ed−1ξ(k + d) in the equation is a random sequence and independent with observed input and output data at time k, k − 1, k − 2, … , equation (B.98) is equal to
B.99 
Without losing generality, we can set ydesired(k + d) = 0, so the minimum-variance control u*(k) can be obtained from the equation
B.100 
that is,
B.101 ![]()
Since the considered system is a minimum-phase system, the polynomial B(q−1) has a stable inverse, and the optimal control to have the variance of the control error minimized is
B.102 ![]()
The minimum-variance control law has a feedback form. A control system diagram with minimum-variance controller is shown in Fig. B.6.
Figure B.6 Minimum-variance control system.

B.103 ![]()
where {ξ(k)} is a sequence of independent random variables with zero mean. Determine the minimum-variance control law u*(k).
B.104 
Solving the following Diophantine equation, we can get the quotient and remainder:
B.105 
Thus, the minimum-variance control law is given as
B.106 ![]()
B.3.2 Self-Tuning Control
Minimum-variance control provides an effective control method for the system in process and measurement noise presence, while adaptive control techniques are used to deal with the variations of the model parameter and operating environment. The fundamental principle of adaptive control is to assess such variations online and then change the control strategy correspondingly to maintain satisfactory control performance.
Self-tuning control is one of the most applied adaptive control methods, in which the parameters of the system model are estimated online by a recursive parameter estimation method introduced in Appendix A. The self-tuning control system shown in Fig. B.7 is a feedback control system which consists of three main functions: parameter estimation, control law modification, and control decision. Since such an adaptive control strategy requires preforming considerable online computations and may also include various aspects of stochastic analysis, the controller must adapt faster than the parameter change rates of the plant and/or environment. In addition, since the shown adaptive control system is an actual feedback control system, the entire system has to be subject to the stability consideration which usually results in complex analysis of system stability, convergence, and performance. This section briefly outlines the widely used minimum-variance self-tuning control.
Figure B.7 Self-tuning control system.

Assuming the system described by (B.79), the minimum-variance self-tuning adaptive controller can be designed based on the following procedure:
B.107 ![]()
B.108 
B.109 ![]()
where

B.110 ![]()
B.3.3 Model Reference Adaptive Control
Model reference adaptive control (MRAC) is another method to adapt the controller to maintain satisfactory system performance according to the changes in the plant or environment. The model reference adaptive control system was originally developed at the Massachusetts Institute of Technology (MIT) for aerospace applications, and the parameter adjustment method is called the MIT rule, where the parameter adjustment mechanism is to minimize the error between model output and actual plant output. The control action u(k) needs to be within the admissible boundary, and normally it is a linear combination of the model output ym(k), reference input r(k), and system output yp(k). The MIT rule-based MRAC design technique is introduced in this section with the control system diagram shown in Fig. B.8.
Figure B.8 Adaptive control system.

A model reference adaptive controller can be designed based on the following procedure:
B.111 ![]()
and a reference model of the form
B.112 ![]()
B.113 ![]()
B.115 ![]()
where ∂e/∂θ is the sensitivity derivative of the system and λ is a parameter that determines the adaption rate.
B.116 ![]()
where the transfer function G(s) is known but the gain k is unknown. Assume that the desired system response is ym(s) = kmG(s)r(s) and the controller is of the form u(t) = θ1 · r(t) + θ2∫r(t), where r(t) is the reference input. Determine an adaptive control law based on the MIT rule.
B.117 
The sensitivity to the controller parameter is
B.118 
Based on the MIT rule, to make the system response follow the desired response, the controller's parameter θ is adjusted as follows:
B.119 
Thus,
B.120 ![]()
The corresponding control system diagram is shown in Fig. B.9.
Figure B.9 Adaptive control system based on MIT rule.

MRAC theory and methodologies have been extensively developed since it was successfully applied to solve aerospace control problems in 1950's. In order to improve the stability of a closed-loop control system, MARC design has been mainly based on Lyapunov's stability theory and Popov's hyper-stability theory since 1970's. The Lyapunov design approach is to find out the optimal control law that is subject to a Lyapunov function for a given plant so the stability of the closed-loop system is guaranteed; however, the drawback of this approach is that there is no a systematic way of finding a suitable Lyapunov function to specify the adaptive control law. On the other hand, Popov's hyper-stability is concerned with finding conditions that must be satisfied to have the feedback system be globally asymptotically stable. These conditions are called Popov integral inequality. According to Popov's hyper-stability theory, the feedback control system is stable if the adaptive control has the closed-loop system satisfy Popov integral inequality. Thus the approach from Popov hyper-stability is much more flexible than the Lyapunov approach to design adaptive control law. For more detailed materials regarding these two approaches, the interested reader is referred to the literature (Åstrom and Witternmark, 1995; Landau, 1979; Butler, 1992).
B.3.4 Model Predictive Control
Model predictive control (MPC), referred to as moving-horizon control or receding-horizon control, is an advanced control technology developed in 1980s which has been widely implemented in practical applications (Garcia et al., 1989). MPC can be formulized as follows.
Assume that the system is described by a single-input, single-output model shown as equation (B.78) or the state space model
B.121 ![]()
where y(k) is the measurable system output, u(k) is the manipulated system input, w(k) is the measurable disturbances, and v(k) is assumed to be white-noise sequences.
Model predictive control is to select the manipulated input variables u(k + i|k), i = 1, … , p at time k which have the following minimum objective function:
B.122 ![]()
subject to
B.123 ![]()
B.124 ![]()
B.125 ![]()
where p and m < p are the lengths of the system output prediction and the manipulated input horizons, u(k + i|k), i = 1, … , p is the set of future manipulated input values which make the objective function minimum, ysp(k) is the setpoint, and Δ is the differencing operator, that is, Δu(k + i|k) = u(k + i|k) − u(k + i − 1|k).
It needs to be emphasized that although the manipulated variables are determined by optimizing the objective function (B.122) over the horizons m, the control action only takes the first step. Therefore, the optimization of MPC is a rolling optimization, and the amount of computation is one of concern when the MPC strategy is implemented in practical applications. The MPC control scheme is shown in Fig. B.10.
Figure B.10 Schematic of model predictive control.

B.4 Fault-tolerant control
Fault-tolerant control is a set of advanced control methodologies which admit that one or more key components of a physical feedback system will fail and such failures can have a significant impact on system stability or other performance. At the simplest level, sensor or actuator failure can be considered, while at a more complex level, subsystem failure needs to be tolerated. In the same vein, engineers can also worry about computer hardware and software failure in the system. The idea of fault-tolerant control design is to retain the stability and safety of the system while losing some performance of the system in a graceful manner. To implement this, it may be necessary to reconfigure the control system in real time following the detection of such failures.
The advancement of hybrid vehicle systems is leading to increasingly complex systems with ever more demanding performance goals. Modern hybrid vehicle systems will require that fault detection, isolation, and control reconfiguration be completed in a short time, and the controller will allow the vehicle to maintain adequate levels of performance even with failures in one or more actuators or sensors; furthermore, the higher degrees of autonomous operation may be required to allow for health monitoring and fault tolerance over certain periods of time without human intervention. Since a practical HEV/PHEV/EV must have the capability of fault accommodation in order to operate successfully over a period of time, fault-tolerant control strategies are necessary to fulfill the safety requirement.
Fault-tolerant control is also a topic of immense activity in which a number of different design and analysis approaches have been suggested. Some mention of such control strategies is desirable, but it is important to realize the nature of fault-tolerant control problems. The briefest coverage is given here to illustrate two fault-tolerant control system architectures.
B.4.1 Hardware Redundant Control
In principle, tolerance to control system failures can be improved if two or more strings of sensors, actuators, and microprocessors, each separately capable of satisfactory control, are implemented in parallel. The characteristics of a hardware redundant control architecture are that the system consists of multiple information processing units each with the same functional objective. The objective may include the generation of control signals and the prediction of system variables. One example of hardware redundant control systems is multiple sensors measuring the same quantity, and the best estimate can be obtained by a majority vote. A hardware redundant control system is illustrated in Fig. B.11.
Figure B.11 Hardware redundant control system.

A voting scheme is normally used for redundancy management by comparing control signals to detect and overcome failures in a hardware-redundant-based system. With two identical channels, a comparator simply determines whether or not control signals are identical such that a failure can be detected; however, it cannot identify which string has failed. In most cases, additional online logics are needed to select the unfailed channel to execute a control task. The design tasks of a hardware-redundant-based fault-tolerant control system usually solve the following problems: selection logic, nuisance trips, generic failures, reliability of voting/selection units, control action contention, cross-strapping, increased cost of operation and maintenance, and number of operating channels required for dispatch. Since the fault detection algorithm is the core functional algorithm, it has to meet higher standard requirements; it must be sensitive to failures yet insensitive to small operational error, including data lost or interrupted due to noncollocation of sensors or actuators. In addition, false indications of failure must be minimized to assure that useful resources are kept online and missions are not aborted prematurely.
B.4.2 Software Redundant Control
A hardware redundant control strategy can protect against control system component failures, but it will increase the cost, make maintenance more difficult, and does not address failures on plant components such as a battery subsystem, transmission, and motors. Furthermore, in the general case, this form of parallelism implies that fault tolerance can only be improved by physically isolating the processors from each other. On the other hand, a software redundant control strategy provides the capability of improving the fault tolerance of the control system on the above three aspects with fewer additional components.
Although hardware redundancy is at the core of most solutions for reliability, uninterrupted operation can also be achieved in control systems through redistribution of the control authority between different functioning actuators rather than through duplication or triplication of those actuators. The idea of a software redundant strategy is to utilize different subsets of measurements along with different system models and control algorithms. In other words, if a variety of system fault patterns and corresponding fault situations are able to be characterized and some possible algorithms can be selected and simulated based on the particular fault pattern, a decision unit will determine the appropriate control algorithm or appropriate combination of algorithms. When the correct algorithm is determined, the control system can be reconstructed against the failures over time. If failures occur within the system, the control algorithm can be changed over time. Software-based redundancy is also called functional redundancy, which mainly consists of a fault detection or diagnosis unit identifying the failed components, controller change, and selection logic units selecting the controller and control channels based on the performance prediction of the selected controller so that the system will adapt to the failure situation. A software redundant control system is illustrated in Fig. B.12.
Figure B.12 Software redundant control system.

References
Åstrom, K. J., and B. Witternmark. Computer Controlled Systems—Theory and Design. Prentice-Hall, Englewood Cliffs, NJ, 1984.
Åstrom, K. J., and Witternmark, B. Adaptive Control, 2nd ed. Addison-Wesley, Reading, MA, 1995.
Bellman, R. E. Dynamic Programming. Princeton University Press, Princeton, NJ, 1957.
Butler, H. Model-Reference Adaptive Control—From Theory to Practice, Prentice-Hall, Englewood Cliffs, NJ, 1992.
Huo, B. C. Automatic Control System, 4th ed. Prentic-Hall, Englewood Cliffs, NJ, 1982.
Garcia, E. C., Prett, M. D., and Morari, M. “Model Predictive Control: Theory and Practice—A Survey,” Automatic, 25(3), 335–348, 1989.
Landau, Y. D. Adaptive Control: The Model Reference Approach. Marcel Dekker, New York, 1979.
Pontryagin, L. S., et al. The Mathematical Theory of Optimal Processes. Interscience, New York, 1962.







