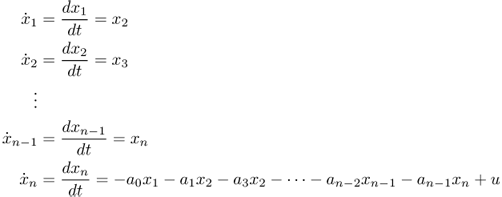Appendix A: System Identification: State and Parameter Estimation Techniques
Building mathematical models of subsystems and components is one of the most important tasks in the analysis and design of hybrid vehicle systems. There are two approaches to building a mathematical model: based on the principles and mechanism as well as the relative physical and chemical laws describing the characteristics of a given system or based on the observed system behaviors. In engineering practice, the architecture of the mathematical model is usually determined from the first approach, and detailed model parameters are determined from the second approach. In this chapter, we introduce basic theories and methodologies used to build a mathematical model and estimate the parameters of the model.
A.1 Dynamic systems and mathematical models
A.1.1 Types of Mathematical Models
The models mentioned in this book are one or a set of mathematical equations that describe the relationship between inputs and outputs of a physical system. These mathematical equations may have various forms such as algebra equations, differential equations, partial differential equations, or state space equations. Mathematical models can be classified as:
- Static versus Dynamic Model A static model does not include time, that is, the behavior of the described system does not vary over time, while a dynamic model does. Dynamic models are typically described by a differential equation or difference equation. Laplace and Fouriers transforms can be applied to the time-invariant dynamic model.
- Time-Varying versus Time-Invariant Model For a time-varying model, the input–output characteristics vary over time, that is, the model parameters differ over time, while a time-invariant model does not. Laplace and Fourier transforms cannot be applied to time-variant systems.
- Deterministic versus Stochastic Model A deterministic model equation is uniquely determined by parameters and previous states of the variables, but different initial conditions may result in different solutions in such models. In contrast, the variables of a stochastic model can only be described by a stochastic process or probability distribution.
- Continuous versus Discrete Model A continuous model is one in which the variables are all functions of the continuous-time variable t. A discrete model differs from the continuous model in that one or more variables of the model are in the form of either a pulse train or digital code. In general, a discrete system receives data or information only intermittently at specific instants of time. For HEV/EV analysis and design, discrete models are mostly used.
- Linear versus Nonlinear Model If a mathematical model is linear, it means that all operators in the model present linearity; otherwise the model is nonlinear. A linear model satisfies the principles of superposition, which take homogeneity and additivity rules together.
- Lumped-Parameter versus Distributed-Parameter Model A lumped-para meter model can be represented by an ordinary differential or difference equation with time as the independent variable. A distributed-parameter system model is described by a partial differential equation with space variable and time variable dependence. Heat flow, diffusion processes, and long transmission lines are typical distributed-parameter systems. Given certain assumptions, a distributed-parameter system can be converted to a lumped-parameter system through a finite-analysis method such as a finite-difference method.
A.1.2 Linear Time-Continuous Systems
A.1.2.1 Input–Output Model of Linear Time-Invariant and Time-Continuous System
For a linear time-invariant and time-continuous system, shown as Fig. A.1, the input–output relationship is normally described by the linear differential equation
where u is the input variable and y is the output variable and coefficients ai, bi are real constants and independent of u and y.
Figure A.1 Input–output system.
For a dynamic system, once input for t ≥ t0 and the initial conditions at t = t0 are specified, the output response at t ≥ t0 is determined by solving equation (A.1).
The transfer function is another way of describing a dynamic system. To obtain the transfer function of the linear system represented by equation (A.1), we simply take the Laplace transform on both sides of the equation and assume zero initial conditions. The result is
A.2 ![]()
The transfer function between u(t) and y(t) is defined as the ratio of Y(s) and U(s); therefore, the transfer function of the system shown in Fig. A.1 is
From equation (A.3), it can be seen that the transfer function is an algebraic equation by which it will be much easier to analyze system performance. The transfer function (A.3) has the following properties:
- The transfer function (A.3) is defined only for a linear time-invariant system.
- All initial conditions of the system are assumed to be zero.
- The transfer function is independent of the input and output.
Another way of modeling a linear time-invariant system is using the impulse response (or weighting function). The impulse response of a linear system is defined as the output response g(τ) of the system when the input is a unit impulse function δ(t).
The output of the system shown in Fig. A.1 can be described by its impulse response (or weighting function) g(τ) as
Knowing ![]() and u(t) for τ ≤ t, we can consequently compute the corresponding output y(t), τ ≤ t for any input. Thus, the impulse response is a complete characterization of the system.
and u(t) for τ ≤ t, we can consequently compute the corresponding output y(t), τ ≤ t for any input. Thus, the impulse response is a complete characterization of the system.
The impulse response also directly leads to the definition of transfer functions of linear time-invariant systems. Taking the Laplace transform on both sides of equation (A.4), we have the following equation from the real convolution theorem of Laplace transformation:
Equation (A.5) shows that the transfer function is the Laplace transform of the impulse responseg(t), and the Laplace transform of the output Y(s) is equal to the product of the transform function G(s) and the Laplace transform of the input U(s).
A.1.2.2 State Space Model of Linear Time-Invariant and Time-Continuous System
In the state-space form, the relationship between input and output is written as a first-order differential equation system using a state vector x(t). This description of a linear dynamic system became a primary approach after Kalman's work on modern prediction control (Goodwin and Payne, 1977). It is especially useful for hybrid vehicle system design in that insight into the physical mechanisms of the system can more easily be incorporated into a state space model than into an input–output model.
A linear stime-invariant and time-continuous system can be described by the state space equation
where x is the n × 1 state vector; u is the p × 1 input vector; y is the q × 1 output vector; A is an n × n coefficient matrix with constant elements,
A.7  B is an n × p coefficient matrix with constant elements,
B is an n × p coefficient matrix with constant elements,
A.8  C is an q × n coefficient matrix with constant elements,
C is an q × n coefficient matrix with constant elements,
A.9 
and D is an q × p coefficient matrix with constant elements,
A.10 
Relationship between State Space Equation and Differential Equation of Dynamic System Let us consider a single-input, single-output, linear time-invariant system described by an nth-order differential equation (A.1). The problem is to represent the system (A.1) by a first-order differential equation. Since the state variables are internal variables of a given system, they may not be unique and may be dependent on how they are defined. Let us seek a convenient way to assign the state variables and make them in the form of equation (A.6) as follows.
For equation (A.6), a way of defining the state variables for equation (A.1) is
where the last state equation is obtained by the highest order derivative term to the rest of equation (A.6). The output equation is the linear combination of state variables and input as
In vector–matrix form, equations (A.11) and (A.12) are written as
where x is the n × 1 state vector, u is the scalar input and, y is the scalar output. The coefficient matrices are
A.14 
A.15 ![]()
Define a state space equation and output equation of the system.
![]()
Then,

that is, the defined state space and output equations of the system are

Relationship between State Space Equation and Transfer Function of Dynamic System Consider that a linear time-invariant system is described by the state space model
where x(t) is the n × 1 state vector, u(t) is the p × 1 input vector, y(t) is the q × 1 output vector, and A, B, C, and D are the coefficient matrices with appropriate dimensions.
Taking the Laplace transform on both sides of equation (A.16) and solving for X(s), we have
A.17 ![]()
Furthermore, it can be written as
Assume that the system has zero initial conditions, x(0) = 0; then equation (A.18) becomes
The Laplace transform of output equation (A.16) is
Substituting equation (A.19) into equation (A.20), we have
A.21 ![]()
Thus, the transfer function is defined as
which is a q × p matrix corresponding to the dimensions of the input and output variables of the system.
A.23 
Determine the transfer function of the system.
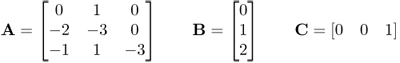
Let

From equation (A.22), the transfer function of the system is

Controllability and Observability of Dynamic System Since state variables are internal variables of a dynamic system, it is necessary to ask if the state variables are controllable by system inputs as well as if they are observable from system outputs. The system controllability and observability will answer the question, and they are defined as follows:
The concepts of controllability and observability are very important in the theoretical and practical aspects of modern control theory. The following theorems provide the criteria judging if the states of a system are controllable and observable or not.
A.24 ![]()
This theorem shows that the condition of controllability depends on the coefficient matrices A and B of the system described by equation (A.13). The theorem also gives a way to test the controllability of a given system.
A.25 
This theorem also gives a way to test the state observability of a given system. The concepts of controllability and observability of a dynamic system were first introduced by R. E. Kalman in the 1960s (Kalman, 1960a and 1960b). However, although the criteria of state controllability and observability given by the above theorems are quite straightforward, it is not very easy to implement for a multiple-input system (Ljung, 1987).
A.1.3 Linear Discrete System and Modeling
In contrast to the continuous system, the information of discrete-time systems is acquired at the sampling moment. If the original signal is continuous, the sampling of the signal at discrete times is a form of signal modulation. A discrete system is usually described by a difference equation, impulse response, discrete state space, or impulse transfer function.
For a linear time-invariant discrete system, its input–output relationship is described by the linear difference equation
where u(k) is the input variable and y(k) is the output variable and coefficients ai, bi are real constants and independent of u(k) and y(k).
If we introduce
A.27 ![]()
equation (A.26) can be written in the form
Taking the z transform on both sides of the equation and assuming zero initial conditions, we will obtain the z-transfer function
A.29 ![]()
The state space model of a linear time-invariant discrete system is as follows:
A.30 ![]()
where x(k) is a n × 1 state vector, u(k) is a p × 1 input vector, y(k) is a q × 1 output vector, and A is an n × n coefficient matrix with constant elements
A.31  B is a n × p coefficient matrix with constant elements
B is a n × p coefficient matrix with constant elements
A.32  C is a q × n coefficient matrix with constant elements
C is a q × n coefficient matrix with constant elements
A.33 
and D is a q × p coefficient matrix with constant elements
A.34 
A.1.4 Linear Time-Invariant Discrete Stochastic Systems
Hybrid vehicle design and analysis engineers exclusively deal with observations of inputs and outputs in discrete systems. In this section, we introduce the linear discrete stochastic systems.
Sampling and Shannon's Sampling Theorem Because of the discrete-time nature of the hybrid vehicle controller, sampling is a fundamental problem affecting control algorithm design. The Shannon sampling theorem presents the conditions that the information in the original signal will not be lost during the sampling. It states that the original continuous-time signal can be perfectly reconstructed if the sampling frequency is equal to or greater than two times the maximum frequency in the original continuous-time signal spectrum, that is,
A.35 ![]()
The following consequences can be drawn from the theorem:
- To assure a perfect reconstruction of the original signal, the lower bound of the sampling angular frequency is 2ωmax for the original signal with the highest frequency component ωmax.
- Or, if the sampling frequency ωsis determined, the highest frequency component of the original signal should be less than ωs/2 for it to be reconstructed perfectly.
- The frequency ωs/2 plays an important role in signal conversions. It is also called the Nyquist frequency.
In the design of discrete-time systems, selecting an appropriate sampling time (Ts) is an important design step. Shannon's sampling theorem gives the conditions assuring that the contained information in the original signal will not be lost during the sampling process but does not say what happens when the conditions and procedures are not exactly met; therefore, a system design engineer who deals with the sampling and reconstruction process needs to understand the original signal thoroughly, particularly in the frequency content. To determine the sampling frequency, the engineer also needs to comprehend how the signal is reconstructed through an interpolation and requirement for the reconstruction error, including the aliasing and interpolation error. Generally speaking, the smaller Ts is, the closer the sampled signal is to the continuous signal. But if the Ts is very small, the actual implementation may be more costly. If Ts is too large, inaccuracies may occur and much information about the true nature will be lost.
Disturbances on a System Based on equation (A.28), the output can be exactly calculated once the input is known, but this is unrealistic in most cases. The inputs, outputs, and parameters of a system may vary randomly with time. This randomness is called disturbance, and it may be of a nature of noise. In most cases, such random effects can be described by adding a lumped item at the output of a regular system model [see Fig. A.2 and equation b01.36]:
Figure A.2 System with disturbance.
A system involving such a disturbance is called a stochastic system, in which measurement noise and uncontrollable inputs are the main sources and causes for such a disturbance. The most distinctive feature of a disturbance is that its value cannot be exactly predicted. However, information about past disturbance can be important for making quantified guesses about coming values. Hence, it is natural to employ a probability method to describe the statistical features of a disturbance. A special case is that if the disturbance term follows a normal distribution, then the statistical features are uniquely described by the mean value μ and the standard deviation σ of the disturbance. Some examples of noise signals are shown in Fig. A.3. In stochastic system control design, control algorithm design engineers must understand the characteristics of the noise signal, and it is necessary to identify whether the behavior of system disturbance/noise is stationary or not. For a stationary stochastic process, the probability distribution is the same over time or position; therefore, some parameters obtained by enough number of tests are valid to describe this type of stochastic process.
Figure A.3 Examples of noise signals.
In practice, the mean value, the standard deviation or the variance, and the peak-to-peak values are the simple features to characterize a stationary stochastic process, although the spectral density function ϕ(ω), which characterizes the frequency content of a signal, is the better representation of the time behavior of a stationary signal. The value ϕ(ω)Δω/(2Π) is the average energy of a signal in a narrow band of width Δω centered around ω.
The average energy in the wide range is defined as
A.37 ![]()
A signal where ϕ(ω) is constant is called white noise. Such a signal has its energy equally distributed among all frequencies.
In HEV control algorithm design, engineers frequently work with signals described as stochastic processes with deterministic components. This is because the input sequence of a system or component is deterministic, or at least partly deterministic, but the disturbances on the system are conveniently described by random variables, so the system output becomes a stochastic process with deterministic components.
Zero-Order Hold and First-Order Hold In a hybrid vehicle system, most original signals are continuous. These continuous signals need to be sampled and then sent to the processor at discrete times. With a uniform sampling period, the continuous signal u(t), shown in Fig. A.4a, will be sampled at the instances of time 0, 2T, 3T, … , and the sampled values, shown in Fig. A.4b, constitute the basis of the system information. They are expressed as a discrete-time function u(kT) or simplified as u(k). The sample-and-hold system is shown in Fig. A.5a; ideally, the sampler may be regarded as a switch which closes and opens in an infinitely short time at which time u(t) is measured. In practice, this assumption is justified when the switching duration is very short compared with the sampling interval Ts of the system. Since the sampled signal u(kT) is a set of spikes, a device is needed to hold them to make the controller able to process them. If the signal is held constant over a sampling interval, it is called the zero-order hold. If the signal is linearly increasing and decreasing over a sampling interval, it is called the first-order hold. The input–output relationships of the zero-order hold and first-order hold are illustrated by Fig. A.5b, c. For a zero-order hold, the output u*(t) holds a constant value during the sampling time period Ts, while a first-order hold generates a ramp signal uh(t) during the sampling period of time Ts. Although higher order holds are able to generate more complex and more accurate wave shapes between the samples, they will complicate the whole system and make it difficult to analyze and design; infact, they are seldom used in practice.
Figure A.4 Continuous and sampled-data functions.
Figure A.5 Input and output of sampler and holder.
Input–Output Model of Stochastic System A linear time-invariant stochastic system can be described by the following input–output difference equation:
where {ξ(k)} is a white-noise sequence which directly indicates the error in the difference equation.
If we introduce
A.39 
a transfer function form model of equation (A.38) can be obtained as
The model (A.38) or (A.40) is called an ARX model where AR refers to the autoregressive part and X refer to extra input B(q−1)u(t) that is the exogenous variable. If a certain degree of flexibility is added to describe the white-noise error in equation (A.38) such as a moving average of white noise, the following model is given:
It can also be written as the form
A.42 ![]()
where u(k) is system input, y(k) is output, w(k) is independent white noise, and A(q−1), B(q−1), C(q−1) are
A.43 
The model (A.41) is called the ARMAX model, which refers to the autoregressive moving-average model with exogenous input model. The ARMAX models are usually used to estimate system parameters online based on real-time measured series data.
State Space Model of Stochastic System The state space model describing a linear time-invariant stochastic system is
where A, B, C, and D are the coefficient matrices with appropriate dimensions and {w(k)} and {v(k)} are two uncorrelated white-noise sequences with covariance Q and R, respectively.
Based on the superposition principle, the model (A.44) can be expressed in terms of two components as
A.45 ![]()
where ![]() is the output of the deterministic model
is the output of the deterministic model
A.46 ![]()
A.47 ![]()
where η(k) is a zero-mean stochastic process having the spectral density
A.48 ![]()
A.2 Parameter Estimation of Dynamic Systems
In this section, we turn to the problem of parameter estimation of a dynamic system. There are many different methods that can be used to determine the parameters of a model, and also there are different criteria on which method should be selected, but we only briefly introduce the basic principle of the least-squares estimation method widely used in engineering.
A.2.1 Least Squares
Least squares is a classic method to deal with experimental data to predict the orbits of planets and comets developed by Gauss in 1795. Unknown parameters of a model should be chosen in such a way that the sum of the squares of the difference between actually observed and computed values is a minimum. Assuming the computed output ![]() is given by the model, the least-squares principle can be mathematically described as
is given by the model, the least-squares principle can be mathematically described as
A.49 ![]()
where x1, x2, … , xn are known inputs, y is output, and θ1, θ2, … , θn are unknown parameters, and ![]()
![]() θn]T.
θn]T.
The pairs of observations {(xi yi), i = 1, 2, … , N} are obtained from an experiment or test. According to Gauss's principle, the estimated parameters should make the following cost function minimal:
If we apply partial derivatives in equation (A.50) and make them equal to zero, that is, ∂J(θ)/∂θ = 0, the solution to the least squares is
where Φ = [φ(1) ![]() φ(N)]T and Y = [y(1)
φ(N)]T and Y = [y(1) ![]() y(N)]T.
y(N)]T.
The above least-squares method can be used to estimate the parameter in the dynamic system described by equation (A.38) or (A.41) with C(q−1) = 1. If we assume that a sequence of inputs {u(1), u(2), … , u(N)} has been applied to the system and the corresponding sequence of output {y(1), y(2), … , y(N)} has been measured, the following vectors can be configured for the least squares described by equation (A.51), and the unknown parameters are θ:
A.52 ![]()
A.53 ![]()
A.54 ![]()
A.55 ![]()
A.2.2 Statistical Property of Least-Squares Estimator
If we assume that the data are generated from the model
A.56 ![]()
where θ0 ∈ Rn is the vector of the theoretical true values of the model parameters, ε ∈ Rn is a vector of white noise with zero mean and variance σ2, that is, E{ ε } = 0 and E{ ε ε T} = σ2I, then the least-squares (LS) estimate of θ0 given by equation (A.3) has the following properties:
A.57 ![]()
It can be proven from

A.58 ![]()
This is derived from
A.59 
The following proof shows that the LS estimator is a consistent estimator; that is, the LS estimate ![]() converges to θ0 as the observation size N tends to infinity. In mathematical terms, if we define limN→∞{[(1/N)ΦTΦ]} = Γ and Γ is nonsingular, then the estimate
converges to θ0 as the observation size N tends to infinity. In mathematical terms, if we define limN→∞{[(1/N)ΦTΦ]} = Γ and Γ is nonsingular, then the estimate ![]() converges to the true value θ0, that is,
converges to the true value θ0, that is, ![]() .
.
A.60 
![]()
If the matrix ΦTΦ is nonsingular, the estimated parameter θ = [a1, a2, b1, b2]T is ![]() . If the persistent excitation is not imposed on the input signals, the matrix ΦTΦ will be singular, resulting in that no unique estimate can be found by the least squares.
. If the persistent excitation is not imposed on the input signals, the matrix ΦTΦ will be singular, resulting in that no unique estimate can be found by the least squares.
A.2.3 Recursive Least-Squares Estimator
In most practical applications, the observed data are obtained sequentially. If the least-squares estimation has to be solved for N observations, the estimate not only wastes computational resources but also overoccupies limited memory. It is necessary to estimate the model parameters in such a way that the N + 1 estimate is performed based on the results obtained for N observations. Parameter estimation techniques that comply with this requirement are called recursive estimation methods. As long as the measured input–output data are processed sequentially, they become available. Recursive estimation methods are also referred to as online or real-time estimation.
Based on N observations y1, y2, … , yN, the least-squares estimate of parameter ![]() is given by equation (A.51) as
is given by equation (A.51) as
A.61 ![]()
where
A.62 
To achieve a recursive least-squares algorithm, we first assume that the parameters ![]() have been estimated based on the N known observations. The objective here is to achieve
have been estimated based on the N known observations. The objective here is to achieve ![]() based on
based on ![]() and just one extra observation yN+1.
and just one extra observation yN+1.
First, we define
A.63 ![]()
Then, we have
A.64 
Based on the matrix inversion lemma introduced below, we have
A.65 
Let
A.66 ![]()
then
A.67 ![]()
Refering to equation (A.61), the following results are achieved from the above equations:
A.68 
so the recursive least-squares estimation method is obtained and summarized as
A.69 ![]()
A.70 ![]()
A.71 ![]()
Matrix Inversion Lemma The matrix inversion lemma states that
A.72 ![]()
where A, C, and A + BCD are regular square matrices of appropriate size.

This completes the proof.
A.73 ![]()
A.74 ![]()
A.2.4 Least-Squares Estimator for Slow Time-Varying Parameters
The recursive least-squares estimation method described in the previous section is not directly applicable when the parameters vary over time as new data are swamped by past data. There are two basic ways to modify the described recursive method to handle time-varying parameters.
Exponential Window Approach (Exponentially Weighted Least Squares) It is obvious that the cost function (A.50) equally makes use of all observed data. However, if the system parameters are slowly time varying, the influence of old data to the parameters is gradually eliminated. The idea of the exponential window approach is to artificially emphasize the effect of current data by exponentially weighting past data values, and this is done by using a cost function with exponential weighting as
A.75 
The λ is called the forgetting factor, 0 < λ < 1, and it is a measure of how fast the old data are forgotten. The recursive least-squares estimation algorithm by using cost function (A.75) is given as
A.76 ![]()
A.77 ![]()
A.78 ![]()
Note that λ = 1 gives the standard least-squares estimation algorithm.
Rectangular Window Approach The idea of the rectangular window approach is that the estimate at time k is only based on a finite number of past data, and all old data are completely discarded. To implement this idea, a rectangular window with fixed length N is set, and whenever a new set of data is added at each time point, a set of old data is discarded simultaneously so the active number of the data points is always kept to N. This approach requires that the last N estimate ![]() and covariance Pi+N, i+1 be stored. For the more detailed algorithm description, the interested reader is referred to Goodwin and Payne (1977).
and covariance Pi+N, i+1 be stored. For the more detailed algorithm description, the interested reader is referred to Goodwin and Payne (1977).
A..2.5 Generalized Least-Squares Estimator
In previous sections, we discussed the statistical property of the least-squares estimation method and stated that the estimate is unbiased if the noise {ξ(k)} in the model (A.7) is a white noise or a sequence of uncorrelated zero mean random variables with common variance σ2. The white-noise assumption is not a practical reality but is suitable for the low-frequency control system analysis of a practical system. If the conditions of the uncorrelatedness and zero mean of the noise sequence {ξ(k)} cannot be satisfied in a system, the statistical properties of the least-squares estimation will not be guaranteed in general. In this case, the generalized least-squares (GLS) method can be used and the estimate is unbiased, which was developed and had been shown to work well in practice (Clarke, 1967; Söderström, 1974).
The idea of the generalized least-squares estimation method is that the correlated sequence {ξ(k)} is considered as the output of a linear filter, which is driven by a white-noise sequence, that is,
A.79 ![]()
where {w(k)} is a white-noise sequence C(q−1) = 1 + c1q−1 + ![]() + cpq−p.
+ cpq−p.
For equation (A.80), we know its z-transfer function is
Then, the system model may be written as
A.81 ![]()
It can be further rewritten as
A.82 ![]()
where
A.83 ![]()
If {y*(k)} and {u*(k)} can be calculated, the parameters in A(q−1) and B(q−1) may be estimated by least squares, and the estimate is unbiased. However, the problem is that C(q−1) is unknown. Thus, the parameters in C(q−1) must be estimated along with A(q−1) and B(q−1), which results in the following generalized least-squares estimation method:
A.3 State estimation of dynamic systems
Some subsystems or components of a hybrid vehicle system are described by the state space model equation (A.44). To control an HEV subsystem properly, the system states sometimes need to be estimated based on observation data. In 1960, Kalman published his famous paper on the linear filtering problem, and his results were named the Kalman filter, which is a set of mathematical equations that provide a recursive computation method to estimate the states of a system in a way minimizing the estimation error (Kalman, 1960). The Kalman filter technique can be summarized as follows:
![]()

A.85 
A.86 ![]()
A.87 ![]()
A.88 
A.89 ![]()
A.90 ![]()
A.91 ![]()
For more details on the probabilistic origins and convergence properties of the Kalman filter, the interested reader is refered to Kalman (1960), Kalman and Bucy (1961), and Jazwinski (1970).
A.92 ![]()
where {w(k)} and {v(k)}, k = 1, 2, … , are Gaussian noise sequences with zero mean and Q and R covariance, respectively. Estimate the state by the Kalman filter technique and list the several step computation values if we assume ϕ = 1, P0 = 100, Q = 25, R = 15.
![]()
From equation (A.90), we have the following prediction error covariance, gain, and filter error covariance:

For the given ϕ = 1, P0 = 100, Q = 25, R = 15, the above equations are given

The results of first several steps are listed in Table Table A.1.
Table A.1 The computation Results of Example A-4

A.4 Joint state and parameter estimation of dynamic systems
In hybrid vehicle applications, it may also be necessary to simultaneously estimate the states and parameters of a subsystem. We devote this section to describe two approaches for joint state and parameter estimation of a dynamic system.
A.4.1 Extended Kalman Filter
While the Kalman filter provides a way to estimate the states of a linear dynamic system, the extended Kalman filter gives a method to estimate the states of a nonlinear dynamics system. To get the extended Kalman filter, we consider the nonlinear dynamic system
A.93 ![]()
where x(k) is the state variable vector, u(k) is the input variable, and y(k) is the output variable; {w(k)} and {v(k)} again represent the system and measurement noises, which are assumed as a Gaussian distribution and independent zero mean with covariances Q and R, respectively.
The extended Kalman filter algorithm is stated as
A.94 
A.95 
A.96 
A.97 ![]()
The iteration process of the extended Kalman filter algorithm is as follows:


The above extended Kalman filter algorithm can be applied to simultaneously estimate states and parameters of a dynamic system. Let us consider the nonlinear dynamic system described by a state space equation (A.93) and assume that there are unknown parameter a in f(x(k), u(k)) and unknown parameter b in g(x(k)). Then equation (A.93) is written as
A.98 ![]()
In order to estimate parameters a and b, we define the a and b as new states, described by the equations
A.99 ![]()
Combining equations (A.98) and (A.99) and letting state variable x*(k) = [x(k), a(k), b(k)]T, an augmented state space equation is obtained as
A.100 
By applying the extended Kalman filter algorithm to equation (A.101), the augmented state x* can be estimated, that is, the estimate of state x as well as parameter a and b are given. There are many good articles presenting practical examples of the extended Kalman filter. The interested reader is referred to the book by Grewal and Andrews (2008).
A.4.2 Singular Pencil Model
The singular pencil (SP) model may be a new class of model for most control engineers and was first proposed by G. Salut and others and then developed by many researchers (Salut et al. 1979, 1980; Chen et al. 1986; Aplevich 1981, 1985, 1991). The SP model contains the input–output and state space model as a subset. Models similar to this form have been called “generalized state space models,” “descriptor systems,” “tableau equations,” “time-domain input–output models,” and “implicit linear systems.” An advantage when a system is described in the SP model format is that the simultaneous state and parameter estimation problem can be solved by an ordinary Kalman filter algorithm.
A dynamic system can be described in SP model form as
where x ∈ Rn is the internal (auxiliary) variable vector and w ∈ Rp+m with known p and m is the external variable vector, usually consisting of input–output variables of the system. Let E and F be (n + p) × n matrices, G be an (n + p) × (p + m) matrix, D a linear operator, and the matrix P(D) also be called the system matrix.
SP models can describe general dynamic systems, which include special cases of two types of most commonly used models: state space and input–output.
If we define
![]()
SP model representation (A.101) can be written as
A.102 ![]()
Equation (A.103) can be readily transformed to the standard state space form as
where u(k) is the input vector, y(k) is the output vector, and (A, B, C, D) are the state space matrices in the usual notation.
The other special case is the ARMAX models with the form
A.104 ![]()
where ai and bi are parameters of the system and q−1 is the shift operator. Equation (A.104) can also be written in first-order SP model form as
When a system is described by the SP model, a Kalman filter algorithm can be used to estimate the state and parameter simultaneously. Let us take equation (A.105) as an example to show how it works. First consider that state x(k) and parameters ai and bj are unknown and need to be estimated and let γ = [an ![]() a1 bn
a1 bn ![]() b0]T and x(k) = [x1(k)
b0]T and x(k) = [x1(k) ![]() xn(k)]T. Then equation (A.105) can be written as
xn(k)]T. Then equation (A.105) can be written as
A.106 
where

In the presence of random disturbances, equation (A.106) is modified as
A.107 ![]()
where e(k) is a zero-mean, uncorrelated vector random variable and C* is a matrix of noise parameters.
If we define the augmented states as
A.108 ![]()
then we have the state space model
A.109 ![]()
By applying the ordinary Kalman filter algorithm described in Section A.3 to equation (A.110), the states and parameters of system (A.105) can be estimated simultaneously.
A.5 Enhancement of numerical stability of parameter and state estimation
In hybrid vehicle applications, parameter and state estimation algorithms are implemented in a microcontroller which normally has limited computational capability. Therefore, improving computational efficiency, enhancing numerical stability, and avoiding unnecessary storage are key factors influencing the implementation of real-time parameter and state estimation for vehicle applications. The following example shows what the numerical stability in real-time parameter/state estimation is, and two techniques are given to overcome the issue in this section.
First, let us consider the following single-parameter estimation by assuming that the model is
where y and φ are output and input, θ is the parameter, and {e(k)} is a uncorrelated white-noise sequence with covariance R.
To present the issue effortlessly, we rewrite the recursive least-squares estimation equation (A.69), (A.70), and (A.71):
A.111 ![]()
A.112 ![]()
A.113 ![]()
Since there is only one parameter in equation (A.110), P and K are scales in equation (A.112) and (A.113). The estimation error can be described as
A.114 
Equation (A.114) is a stochastic difference equation, and it is unstable when |1 − K(k + 1)φ(k + 1)| > 1 or when K(k + 1)φ(k + 1) < 0, which will result in estimated parameter blow-out.
From gain equation (A.112), we know that
A.115 ![]()
and from the above equation, we obviously find that the unstable condition K(k + 1)φ(k + 1) < 0 is equal to
A.116 ![]()
In other words, if the covariance matrix P is negative, the estimate will be unstable until P(k)φ2(k + 1) is less than − 1. Also from covariance equation (A.113), we know that P(k + 1) is negative when K(k + 1)φ(k + 1) > 1. In addition, equation (A.115) shows that K(k + 1)φ(k + 1) → 1 when the value of P(k) is big enough, and it results in the instability of the recursive calculation of the covariance matrix P(k).
To solve the unstable issue of the recursive least-squares estimation, it is necessary to have the covariance matrix be strictly positive definite. In this section, we introduce two common algorithms to achieve the goal.
A.5.1 Square-Root Algorithm
The square-root algorithm is an effective technique to improve the numerical stability of the parameter estimation (Peterka, 1975). Since the covariance matrix P needs to be strictly positive definite, P can be factorized into the form
A.117 ![]()
where S is a nonsingular matrix called the square root of P.
In a recursive least-squares estimation algorithm, if the S is updated rather than P in real time, the strictly positive definite of P is promised. The corresponding recursive algorithm for equation (A.110) can be derived as follows.
If we have
A.118 
the covariance matrix P can be expressed in the recursive form
A.119 
or
![]()
Hence, the parameters can be estimated based on the following square-root recursive least-squares estimation algorithm, and the numerical stability is promised:
A.120 
A.5.2 UDUT Covariance Factorization Algorithm
Since the square-root-based recursive least-squares estimation algorithm requires extraction of the square root in real time, the computational efficiency is relatively low. Thornton and Bierman (1978) proposed an alternative approach to achieve the numerical stability of the estimation, but it does not require square-root extraction. In their algorithm, both accuracy and computational efficiency are improved by using covariance factorization P = UDUT, where U is upper triangular with unit diagonals and D is diagonal. Compared with the general recursive least-squares estimation algorithm, U–D factorization based recursive least-squares estimation algorithm updates covariance factors U and D together with gain K in real time (Thornton and Bierman, 1978).
If we assume that the computed output y is given by the model
A.121 ![]()
where x1, x2, … , xn are inputs, y is the output, θ1, θ2, … , θn are unknown parameters, and {e(k)} again represents measurement noise following the Gaussian distribution with independent zero mean and covariance R. The pairs of observations {(xi, yi), i = 1, 2, … , N} are obtained from measurements if θ = [θ1θ2 ![]() θn]T and
θn]T and ![]() .
.
The parameter vector θ can be estimated by the following U–D factorization-based recursive least-squares algorithm once the measured input and output and initials of ![]() , and D(0) = D0 are given:
, and D(0) = D0 are given:
A.122 
A.123 
A.124 
A.125 
A.126 
where U(k) ∈ Rn×n is a upper triangular matrix with unit diagonal, D(k) ∈ Rn×n is a diagonal matrix, F(k) and G(k) ∈ Rn are vectors, β is a scalar, and λ is the forgetting factor.

Calculate the corresponding variables of the UDUT covariance factorization algorithm:

A.6 Modeling and parameter identification
The modeling task is to build a mathematical relationship between the inputs and outputs of a system, which is normally expressed by a set of dynamic equations which are either ordinary differential equations or partial differential equations. In the steady-state case, these differential equations are reduced to algebraic equations or ordinary differential equations, respectively.
As mentioned earlier, there are two approaches to accomplishing the modeling task: through theoretically deriving and analyzing the system based on physical/chemical principles or computing from the observed (measured) data from special experiments or tests. The model achieved from the first approach is a theory-based model and takes in the basic physical and chemical rules as well as the continuity equations, reaction mechanisms (if known), diffusion theory, and so on. The major advantages of a full theoretical model are the reliability and flexibility allowing for major changes in system architecture and predicting behavior into the wide operating range. However, this ideal situation is often seriously undermined by a lack of precise knowledge and the need to make assumptions which need to be verified sometimes. Even then, the extremely complex nature of many system models can make their solution impossible or economically unattractive.
The model established from another approach is the data-based model. The acceptance of the data-based model is guided by usefulness rather than truthfulness, which means that such a model has a good input–output relationship under a certain operating range but can never establish any exact meaningful connection between them. In the absence of other knowledge or in difficult-to-define systems, this method is most important. The shortcoming of this approach may lead to misleading conclusions resulting from missing essential data or error in data. Although this identification method may yield fruitful relationships, validations in the wide operating range are necessary to ensure the established model technical sound. In general, building a system model needs to undergo the following six procedures.
Determine Objectives of Modeling First, the purpose of the model must be clearly defined, which plays a key role in determining the form of the model. It must be decided initially and recognized that the model developed specifically for one purpose may not be the best, or even a suitable form for another purpose. If the developed subsystem model is to support the overall performance analysis of the whole hybrid system, the model should be small and relatively simple. Increase in overall system complexity may require a reduction in the detail of modeling of specific units or subsystems. In addition, the boundaries of the model variables also need to be taken into account.
Gather Prior Knowledge of System It is very important to gather enough prior knowledge of a system, which can save modeling cost and time. Prior knowledge for modeling includes theoretical understanding, practical engineering intuition, and insight on the system, such as main input variables (factors), their varying ranges and limits, and environmental noise mean and variance.
Choose Candidate Model Set This is a key step in modeling practice. Before a model has been developed, based on prior knowledge, a candidate model set and all necessary variables must be identified for the system behavior to be adequately described. The variables fall essentially into two categories: independent variables, also known as input variables, and dependent, or output, variables. Usually a simple form of the model should be used for a subsystem if the overall performances of a large system are concerned. Because a system interacts with others, boundaries of the model also need to be decided upon. To some extent, the boundaries determine the size and complexity of the model.
Design Experiment and Record Data To identify a dynamic system, the system must be excited enough to have recorded data sufficiently informative. Therefore, a design needs to be carried out for an identification experiment, which includes the choice of input and measurement ports, test signals, sampling rate, total available time, and availability of transducers and filters. Also, the experimental design must take into account the experimental conditions, such as constraints and limits, and the operating points of the system. The minimum requirement to the input signals is that the input signal must be able to excite all modes to the system, that is, the input signal has to meet the requirement of persistence of excitation. For the more detailed experimental design problems, the interested reader is referred elsewhere (Goodwin and Payne, 1977; Ljung, 1987).
Estimate Model Parameters After selecting a set of candidate models and collecting enough data, one can start to estimate the parameters of the model. It needs to be emphasized that there are many methods of estimating the parameters and also different views of judging whether the estimated results are good. The common estimation methods, excluding least squares or generalized least squares introduced in this chapter, are maximum likelihood, instrumental variable, and stochastic approximation. Readers should select one of them to estimate model parameters based on the purpose of the model and prior knowledge of noise.
Validate Model Validation is to test if the established model can meet the modeling requirements. An important validation is to evaluate the input–output behavior of the model to see if the model's outputs can match with actual measured outputs resulting from the same input values. This is carried out through a process which simulates the system with the actual inputs and compares measured outputs with the model outputs. Preferably, a different data set is used for the comparison than the one used for the modeling. If the validation tests pass, the modeling task is done; otherwise, we need to go to procedure B to refine prior information on the system and redo procedures C to F.
Aplevich, D. J. “Time-Domain Input-Output Representations of Linear Systems.” Automatica, 17, 509–521, 1981.
Aplevich, D. J. “Minimal Representations of Implicit Linear Systems.” Automatica, 21, 259–269, 1985.
Aplevich, D. J. Implicit Linear Systems: Lecture Notes in Control and Information Sciences, Vol 152, Springer-Verlag, Berlin, 1991.
Chen, Y., Aplevich, D. J., and Wilson, W. “Simultaneous Estimation of State and Parameters for Multivariable Linear Systems with Singular Pencil Models.” IEE Proceedings, Pt. D, 133, 65–72. 1986.
Clarke, D. W. “Generalized Least-Squares Estimation of the Parameters of a Dynamic Model.” Proceedings of IFAC Symposium on Identification in Automatic Control Systems, Prague, 1967. International Federation of Automatic Control (IFAC) (http:// www.ifac-control.org).
Goodwin, G. C., and Payne, R. L. Dynamic System Identification: Experiment Design and Data Analysis-Mathematics in Science and Engineering, Academic Press, New York, 136, 1977.
Grewal, S. M, and Andrews, P. A. Kalman Filtering: Theory and Practice Using MATLAB, 3rd ed. Wiley, Hoboken, NJ, 2008.
Jazwinski, A. H. Stochastic Processes and Filtering Theory. Academic, New York, 1970.
Kalman, R. E. “On the General Theory of Control Systems.” Proceedings of First IFAC Congress, Moscow, Vol. 1. Butterworths, London, 1960a, pp. 481–492.
Kalman, R. E. “A New Approach to Linear Filtering and Prediction Problems.” Transactions of ASME, Journal of Basic Engineering, 82, 34–45, 1960b.
Kalman, R. E., and Bucy, R. S. “New Results in Linear Filtering and Prediction Theory.” Transactions of ASME, Journal of Basic Engineering (Ser. D), 83, 95–108, 1961.
Ljung, L. System Identification Theory for the User. Prentice-Hall, Englewood Cliffs, NJ, 1987.
Peterka, V. “A Square Root Filter for Real-Time Multivariable Regression.” Kybernetika, 11, 5A–67, 1975.
Salut, G. J., Aquilar-Martin, J., and Lefebvre, S. “Canonical Input-Output Representation of Linear Multivariable Stochastic Systems and Joint Optimal Parameter and State Estimation.” Stochastica, 3, 17–38, 1979.
Salut, G. J., Aquilar-Martin, J., and Lefebvre, S. “New Results on Optimal Joint Parameter and State Estimation of Linear Stochastic Systems.” Transactions of ASME, Journal of Dynamic Systems Measurement and Control, l02, 28–34, 1980.
Söderström, T. “Convergence Properties of the Generalized Least-Squares Identification Method.” Automatica, 10, 617–626, 1974.
Thornton, C. L., and Bierman, G. J. “Filtering and Error Analysis via the UDUT Covariance Factorization.” IEEE Transactions on Automatic Control, AC-23(5), 901–907, 1978.