Chapter 2
Main Physical Features of Electromagnetic Cavities
2.1. Introduction
We will recall in this chapter the physical principles of reverberation chambers, partly based on the features of electromagnetic cavities. We will not recall the mathematical formulation details of the fields and of the couplings within cavities. There are many excellent books on this topic that we recommend readers consult beforehand. Instead we will take a more specific look at the behavior of the oversized cavities, cavities excited via continuous sinusoidal sources; these sources release a wavelength much smaller than their dimensions. With this purpose, the theory developed in section 2.2 will merely consist of a one-dimensional (1D) cavity made up for that reason of a coaxial line, closed at both ends by perfect short-circuits. This very simplified vision offers the advantage of analyzing the physical behavior of a common cavity, thanks to the currents and voltages coming from the transmission line theory. Thanks to this device, admittedly far from a real chamber, we reach the calculation of the eigenmodes and the assimilation of the cavity to an assembly of electric resonators made up of inductances, capacitances and conductances. This additional simplification will facilitate the rise of the quality factor concept. Its use will be essential to the physical understanding of mode stirring and other features of reverberation chambers.
Section 2.3 is the natural continuity of the previous section, being fully devoted to the study of rectangular cavities. This section, subdivided into nine parts, progressively tackles the analysis of TE and TM modes, and then considers the impact of oversizing, illustrated by the modal cells concept. This presentation also has the advantage of introducing the physical understanding of mode stirring and of modal interferences depending on the quality factor of the chamber. Coming back to the 1D model, this time a Fabry-Perot cavity, will allow us to introduce the coupling of the electromagnetic energy on an eigenmode and consecutively to find the intensity of the standing wave in a cavity. The plane wave spectrum concept will then be defined, in order to prepare the reader for the simulation of ideal random fields, developed in the next chapter.
Section 2.4, concluding this chapter, will be devoted to the brief analysis of the mode stirring processes. From this intuitive approach of the phenomena, we will be able to see that a properly carried out stirring must produce electromagnetic fields, whose amplitude distribution obeys the perfect random model. Later on, research into this criterion will enable us to determine the uncertainty margins and consequently to ensure the reproducibility of the measurements carried out in the MSRC.
2.2. Reduction of the modes in a 1D cavity
2.2.1. Description of the 1D cavity
Understanding the physical behavior of an electromagnetic cavity can be significantly simplified by the use of a 1D model, made up of a coaxial cable sample, short-circuited at both ends. Indeed, this device constitutes a transmission line that is much simpler to form in equations than a three-dimensional cavity. Figure 2.1 specifies the geometrical parameters useful for calculations.
Figure 2.1. ID cavity

The inside part has a tube terminated at both ends by high-conductivity disks carrying out two perfect short-circuits. The device forms a transmission line. The propagation of the TEM mode assumes, however, that the wavelength remains much higher than the diameter of the outer cylindrical tube. We associate with this set a single graph oz, in parallel with the common axes of the two cylinders. The origin o coincides with one of the ends of the coaxial. Its longitudinal dimension will be designated by the symbol L0. We thus have at our disposal a cavity with an extremely simple constitution, for which it will be easy to transpose the transmission line theory, recalled in the next section.
2.2.2. Solutions of the 1D waves equation
2.2.2.1. General waves equation
With the use of the notations in Figure 2.2, the currents and voltages attached to the cavity will successively be represented by the functions i(z,t) and v(z,t) of the space variable z and of the time variable t.
Figure 2.2. Conventions of the currents and voltages on the line

The set of the two telegrapher equations leads to a waves equation containing the unknown functions i(z,t) or v(z,t). For the current, we find waves equation [2.1], which is similar to the equation established in [1.2] of Chapter 1 for the plane wave:
[2.1] 
In this second-order partial differential equation, v0 corresponds to the propagation speed of the currents and voltages. Knowing that the cavity in Figure 2.1 is empty, v0 is the speed of light in vacuum, so-called celerity c, for which we will adopt the approximate numerical value shown in [2.2].This is justified in section 1.2.1.1 of the previous chapter.
[2.2] ![]()
2.2.2.2. Waves equation for the harmonic steady state
If we assume the cavity is excited by a harmonic source of angular frequency ω, after extinction of the transient state, we can show that the functions i(z,t) or v(z,t) take the steady state established by complex notations of [2.3]:
[2.3] ![]()
Complex notations are adopted by convenience. In fact, the signal corresponds to the real component of one of these two expressions. Under this representation, I(z) and V(z) are complex functions of the space variable z. After the introduction into the initial wave equation [2.1], we reach the waves equation of the harmonic steady state:
[2.4] 
The k parameter is called the wave number. This is the ratio of the excitation angular frequency and of the v0 propagation speed of the wave. Moreover, we can demonstrate that the propagation speed is directly related to the inductance per unit length L and to the capacitance per unit length C of the line, thanks to expression [2.5] recalled below:
[2.5] ![]()
2.2.2.3. Waves equation solutions
Solutions to waves equation [2.4] are exponential functions with an imaginary exponent, presented in the usual equation [2.6] [DEM 03, GRI 69]:
[2.6] ![]()
It is then easy to deduce the voltage solution represented by the function V(z) in which we can find the characteristic impedance Zc of the line; this is the square root of the ratio of the inductance per unit L and of the capacitance per unit length C:
[2.7] 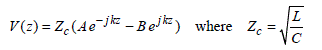
Sometimes, solutions [2.6] and [2.7] are shown with the operand of the exponential function as exponenting the product of variable z and propagation constant γ that we simply contract to wave number k by the product of imaginary number j:
[2.8] ![]()
The propagation constant γ appears when we take into account the power losses in the line. In that case, γ takes the form of a complex number, with α being the real part and t β being the imaginary part. The latter will generally be similar to the wave number k.
The main interesting fact of the comparison to a 1D cavity is first the computation for resonances of the cavity, more succinctly called eigenmodes.
2.2.3. Eigenmodes computation
The short-circuits placed at both ends of the line vanish the voltages on the two terminations.
Carrying forward on the notation conventions in Figure 2.2 and on the function developed in [2.7] leads to [2.9]:
[2.9] ![]()
This is an undetermined system and its constants A and B are the solutions. To fill the cavity with electromagnetic energy, these constants must take finite values and the trivial solution is ignored. This condition thus implies cancelling the determinant of the system.
Thus, we manage to solve the equation with eigenvalues [2.10], whose immediate solutions are found on the right side of the equation with the symbol kn:
[2.10] ![]()
The calculation reaches an infinite spectrum of eigenvalues kn, called eigenwave numbers. Their value is inversely proportional to the dimension L0 of the 1D cavity. These specific wave numbers, still called eigenmodes, are dependent on the integer number n that determines their position of appearance.
As shown in Figure 2.3, if we feed the cavity with a current source of amplitude I0 located at the point of coordinate z0, the voltage variation as a function of the space variable z will be determined by two functions V1(z) and V2(z), depending on whether the observer is located above or below z0.
Figure 2.3. Excitation of the 1D cavity by a current source

The functions then take the analytical expressions [2.11] and [2.12]:
[2.11] 
[2.12] ![]()
Knowing that the wave number depends on the angular frequency of the source, as well as on the frequency by [2.13], a look at the previous equations shows that the excitation of the cavity on a frequency rigorously equal to the frequency fn attached to the eigenmode of index n, produces a voltage with an infinite amplitude. Resonance of the cavity occurs in a similar way to a circuit made up of an inductance or a capacitance connected in parallel:
[2.13] ![]()
Contrary to the usual theory of the LC circuits where only one resonance specified by the circuit components is involved, the 1D cavity has an infinity of resonances, periodically spaced out from the value Δf.
The aforementioned is made up of a ratio in which the dimension L0 and the propagation speed of the waves v0, here reduced to the celerity c, are introduced:
[2.14] ![]()
The analogy with the circuits can be used in order to demonstrate that a cavity excited on any frequency is the series of a very large number of resonators, made up of inductance and capacitance cells connected in parallel.
2.2.4. Comparison of a cavity to a network of LC resonators
According to Foster’s theorem, the reactance X(ω) at any point of every electromagnetic cavity takes the form of a series expressed under configuration [2.15] [ELF 10, LEM 09, RAG 48]:
[2.15] 
This relation is established with the assumption of perfectly electrically conducting walls of the cavity. The cavity impedance is then determined by the ratio of the electric field and of the magnetic field either deduced from computations or measurements. Concerning the particular case of the coaxial cavity in Figure 2.3, X(ω) will result from the ratio of the voltage calculated at the point z0 and of the current I0 injected by the source.
The Cn capacitances found in equation [2.15] are related to endless number of resonators, made up of inductances and capacitances connected in parallel, whose resonance angular frequencies are adjusted on the angular frequency ωn of the eigenmode of index n, i.e.:
[2.16] ![]()
For the 1D cavity, the resonance frequency fn appearing in this equation is the modal frequency fn calculated in [2.13]. The Cn capacitances are expressed in terms of an admittance which is the product of the imaginary number j and a function B(ω) so called susceptance, at the considered point and by application of relation [2.17]:
[2.17] 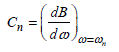
Then, back to the 1D cavity in Figure 2.3, the B(ω) susceptance is found from the sum of the admittances found in the AA’ and BB’ planes, i.e.:
[2.18] ![]()
From the transmission line theory, we easily deduce YAA’ and YBB’:
[2.19] 
The inductances are then obtained from expression [2.16]. With regard to the c0 coefficient, the calculation comes from relation [2.17], extended to the vanishing angular frequency, i.e.:
[2.20] 
Regarding c0 and l0, their contribution is only justified for the study of the 3D cavity. Indeed, these parameters characterize the electromagnetic coupling from the source to the cavity.
Applied to the 1D cavity, this expression leads to an infinite capacity. We easily find the value of the coefficient l0 by the calculation of the first derivative of relation [2.15] with respect to the angular frequency ω, that we will also make strive towards zero, i.e.:
[2.21] 
For the 1D cavity, this calculation leads to the inductance l0 vanishing.
The series appearing in [2.15] is similar to an assembly of resonators as given in Figure 2.4. This assembly is located between the AA’ and BB’ planes of the line in Figure 2.3 where current source is placed.
Figure 2.4. Comparison of the 1D cavity to an assembly of resonators: in that case l0 = 0 and c0 = 0
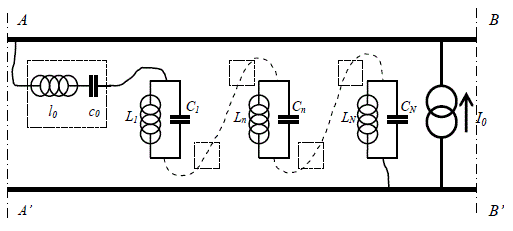
Transposed to the 1D cavity, the coupling inductance l0 and the coupling capacitance c0 a may be omitted.
Contrary to the complete series expansion in equation [2.15], the diagram in Figure 2.4 is bounded to N resonators, i.e. the calculation is limited to the Nth order. This convenience is essential when we have to carry out numerical simulations. Note that the empty squares correspond to the N-3 resonators absent from the figure.
The use of this assembly of resonators simplifies the understanding of some physical phenomena encountered in the cavities, such as in the case of the quality factor. Indeed, the diagram in Figure 2.4 shows that, when fed by a sine wave current source I0 f with angular frequency ω, the reactance X(ω) tends to infinity as soon as ω tunes with one of the angular frequencies of resonance ωn of the resonators. Now, if we imagine that the line is supplied by a similar source whose angular frequency tunes exactly with ωn, the cavity reaches the eigenmode “n”. We can show that the maximum and minimum amplitudes of the voltage observed on the resonator “n” continuously increase and this is proportional to the time variable. This phenomenon may be related to the addition of the multiple reflections of the currents and voltages occurring at both ends of the cavity. Let us consider the contribution of the losses due to the conductors of the line or coming from the internal conductance of the current source. As soon as these various losses get involved, the use of the circuit theory shows that the transient state eventually evolves towards a steady state. And the resulting sine wave reaches finite amplitude. For durations longer than the damping time constant, calculations of the response can be carried out using the usual concepts of impedances and admittances.
2.2.5. Contribution of the quality factor to the cavity
First, we make the assumption that the current source presented in Figure 2.3 has no internal conductance. Consequently, the amplitude of the currents and of the voltages during resonances is dependent on the only thermal losses in the conductors constituting the cavity.
The transmission lines theory involves that the losses in the conductors can be gathered in a complex propagation constant γ: including as an imaginary part, the wave number k recalled in [2.19]; and as a real part, the coefficient α, called the (per unit length) attenuation of the line.
If it is a line with low losses (which is generally the case when we carry out cavities), a good approximation of α can be given by the formula on the right side of equation [2.22]:
[2.22] 
The characteristic impedance of the line Zc and its resistance per unit length R appear in this formula. With frequencies higher than 10 MHz the skin depth of the currents in high conductive materials is so low that we can use for the per unit length resistance of the coaxial line in Figure 2.1 the approximation related below:
[2.23] 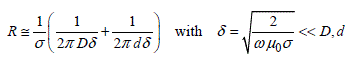
In these formulas, we have the electric conductivity σ of the material, the skin depth δ, as well as the outer diameter D and inner diameter d.
Inserting the contribution of thermal losses in equations [2.19], the admittances formulas in the AA’ and BB’ planes will be modified to the new expressions [2.24], containing the hyperbolic tangent functions:
[2.24] 
With the assumption of high-conductivity materials, such as copper or steel, the product αL0 appears to be much lower than unity. The expressions in [2.24] then take as approximate forms:
[2.25] ![]()
[2.26] ![]()
When we start the calculation of these expressions on an eigenmode n, we can show – after using some additional simplifications not mentioned here – that the equivalent admittance Yeq found at the location of the current source takes the form:
[2.27] ![]()
This formula, only valid for the angular frequencies ω not too far from the angular eigenfrequency ωn, has the B(ω) susceptance established for the line without losses in [2.18]. Then, there is a conductance term Gn that we can link to the pul (per unit length) attenuation α, to the characteristic impedance Zc, as well as to the geometrical data z0 and L0.
If we take a look at the diagram in Figure 2.4, this conductance must be placed on the resonator of index n, to be related with the usual definition of the quality factor Qn, of the circuit theory, i.e.:
[2.28] 
The contribution of losses thus bounds the voltage amplitude during resonance. The latter takes the value Vn determined by the ratio of I0 and of the conductance Gn:
[2.29] 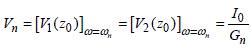
If we designate the symbol WE n to the electric energy stored in the cavity during a Tn period of the sine wave voltage established under the resonance angular frequency ωn, and if we call Pd n the thermal power dissipated in the cavity, we manage to express WE n and Pd n with the help of relation [2.30], where appear the rms amplitudes of I0 and Vn: (rms stands for root mean square)
[2.30] 
The combination of [2.28] and [2.30] leads to the energetic relationship of the quality factor, i.e.:
[2.31] 
Knowing that the electric energy is balanced by an exchange of magnetic energy WM n, relation [2.31] is rigorously similar when we substitute WM n for WE n.
The definition of Qn requiring the energy will find its use during the analysis of 3D cavities, examined in the next section.
The power dissipated into the conductive materials of the 1D cavity previously studied does not constitute the only losses affecting the value of the quality factor.
If the I0 current source has internal conductance G0, the power at the denominator in relation [2.30] takes expression [2.32]:
[2.32] 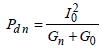
In addition to the condition required by putting the cavity excited on an eigenmode into resonance, we will show in the next section that the level of the electromagnetic energy stored in the cavity will also depend strongly on the z0 position of the current source.
2.2.6. Optimal coupling of the energy on an eigenmode
Let us return to relation [2.7], expressing the voltage on the line, as we have taken it from the resolution of the wave equation. When the cavity is excited on the eigenmode n, it is necessary to add the index n on the parameters of equation [2.7] i.e.:
[2.33] ![]()
Since the voltage vanishes at both ends of the cavity, the use of Euler formulas for Vn(z) leads to sinusoidal function [2.34]:
[2.34] ![]()
We will show that the V0n amplitude assigned to this particular mode will depend on the position of the current source. The intuition inspired from the examination of Figure 2.3, very clearly shows that the current source positioned in a z0 point, where the function Vn(z) is cancelled, is unable to introduce energy into the cavity, even if it is excited on one of its eigenmodes. This reasoning means that at this particular position, the B(ωn) susceptance in expression [2.18] must be infinite. The current injected in z0 implies the voltage strictly vanishes as well as, consecutively, the electric energy WE n. However, if we take into account the contribution of the losses due to high-conductivity materials, values of the voltage and storage electric or magnetic energies will be only close to zero. When the cavity is no longer tuned on an eigenmode, V(z) goes far from the purely sinusoidal function described above. The analytical formulation of V(z) can then be built thanks to a series expansion, in which the solutions of [2.34] are the basic functions of index n. The V(z) voltage distributed on the cavity thus takes the form of a series, where the V0n amplitude terms play the similar role of Fourier coefficients:
[2.35] 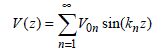
It is interesting here to introduce the wavelength λ, related to the propagation speed v0 and frequency as given in formulas [2.36]:
[2.36] 
From equation [2.13] which express the fn frequency of the eigenmode of index n, we find that tuning the cavity on the n mode amounts to feed the line with a sinusoidal (sine wave) signal, whose λn/2 half wavelength rigorously matches one sub-multiple of the L0 dimension of the cavity, i.e.:
[2.37] ![]()
From this point of view, a cavity exactly tuned as formulated in [2.37] produces in series [2.36] coefficients that are all zero, except for V0n. Otherwise, we go to an infinite spectrum of coefficients.
When the λ wavelength is very small compared to L0, the cavity is said to be oversized. Under these conditions and without a rigorous tune on a mode, we can show that the amplitude of the coefficients goes through a maximum at the neighborhood of the L0/n which is the closest to λ/2.
2.2.7. Deviation of the modal frequencies produced by an obstacle
An obstacle may be a piece of high-conductivity material inserted in the gap between the inner and outer conductor of the line. Let us take a look at an obstacle installed at the point of coordinate zk shown in Figure 2.5. With the prior assumption that the obstacle remains with small dimensions compared to the wavelength λ, its physical contribution may be accounted (taken into account) by an equivalent circuit, comprising the combination of the Lk inductance and the Ck capacitance, linked in Figure 2.5. The presence of the obstacle thus forces us to distinguish two pairs of solutions, depending on whether the z variable is higher or lower than zk. In the first case, the unknown amplitude parameters in expressions [2.6] and [2.7] take as symbols A1 and B1. In the second case, we use the symbols A2 and B2.
Figure 2.5. Circuit equivalent to an obstacle introduced in the cavity
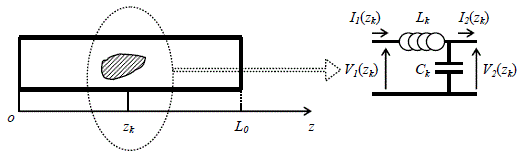
The algebraic system thus has for instance four unknown values that we manage to connect using the boundary conditions at both ends of the line and on the drawn circuit at the point of coordinate zk. The calculation leads to the combination of four equations, leading themselves to a linear system with A1, B1, A2 and B2 as solutions:
[2.38] ![]()
[2.39] ![]()
[2.40] ![]()
We find again a configuration quite similar to the empty cavity, since the combination of equations [2.38] to [2.40] leads to an indeterminate fourth order system. The search for non-singular solutions leads us to impose a strictly zero value on the system determinant. This condition leads to the resolution of a transcendental equation, whose ωn roots form a spectrum of eigenvalues necessarily different from those found for an empty cavity. However, the physical good sense suggests that, in the presence of a tiny obstacle, the angular eigenfrequencies found on this little disturbed cavity will be almost in agreement with the values predicted by initial formula [2.13].
Conversely, as soon as the impact of the obstacle becomes significant, we observe a more significant shift of the eigenmodes. According to this new context the analogy of the cavity with an association of resonators made up of capacitances and inductances remains valid. However, the determination of the values of the inductances Ln and capacitances Cn making up each element of the circuit in Figure 2.5 must be revised, by using a numerical calculation.
A similar comment can be applied to series expansion [2.35] describing the V(z) function. Indeed, we have pointed out that the description of the Vn(z) voltage attached to the n mode, differs from a sinusoidal function as previously used. Consequently, the extension of this reasoning encourages us to change the nature of the functions involved in the series expansion, taking this time the general form [2.41]:
[2.41] 
When it is possible, the new Vn(z) functions will be evaluated thanks to solutions [2.6] and [2.7] attached to the n mode, extracted from the resolution of the equations with the eigenvalues previously described.
2.2.8. Implementation of mode stirring
If we add to the diagram of Figure 2.5, a current source at the point of coordinate z0 and an observer taking the voltage at the point zp, we go straight to the circuit in Figure 2.6.
Figure 2.6. Illustration of mode stirring

Under these conditions, a displacement of the obstacle parallel to the oz axis has the effect of modifying the eigenmodes frequency, as well as the amplitude of the voltage seen by the observer. If we sufficiently increase the frequency so that the wavelength becomes comparable to the longitudinal dimension of the obstacle, the organization of the modes is so disturbed that it becomes hardly predictable. In other words, we can say that the voltage variation as a function of the zk position of the object adopts the behavior of a random variable. This phenomenon is increasingly amplified, if we introduce into the cavity other obstacles that move independently from the displacement of the previous obstacles. This device carries out a mode stirring, whose properties will be fully exploited in the use of the reverberation chambers discussed in the following sections of this chapter.
2.3. Physical features of an empty rectangular cavity
2.3.1. Geometrical description of the reverberation chamber
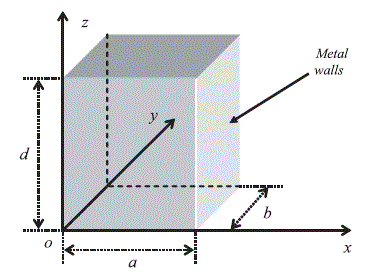
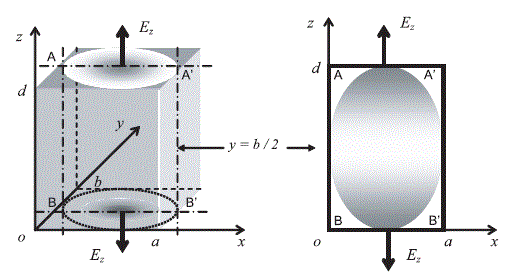
The reverberation chamber that we will compare to a rectangular cavity has the dimensions a, b and d, shown in Figure 2.7. To designate the height of the chamber, the letter d is preferred to the letter c, in order to avoid confusion with the common symbol for the electromagnetic waves speed in a vacuum (celerity).
Currently, the chamber is devoid of any object diffracting or absorbing the waves. We can add to this hypothesis the contribution of the walls made up of a material with a very high electric conductivity, such as copper or steel.
On the left lower angle of the front face shown in Figure 2.7, we set the orthonormal coordinate system oxyz.
Figure 2.7. Geometrical parameters of the rectangular chamber
2.3.2. Calculation of the eigenmodes’ frequencies
We install in the chamber an antenna radiating an electromagnetic field releasing sinusoidal signals. The ω angular frequency of the signals is linked to the f frequency by the well-known expression recalled below:
[2.42] ![]()
As previously practiced for the 1D cavity, the preliminary analysis will be carried out with the chamber empty. We assume that the transmitting antenna does not alter the distribution of the field amplitude in the whole internal volume of the cavity.
Under these circumstances, wave equation [2.43] adapted to the 3D context must correspond to wave equation [2.4] established for 1D:
[2.43] 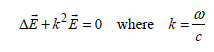
There is in this expression the ![]() electric field vector distributed inside the empty chamber. Developments available in most electromagnetism books enable us to go from Maxwell’s system of equations, recalled below, to waves equation [2.43]:
electric field vector distributed inside the empty chamber. Developments available in most electromagnetism books enable us to go from Maxwell’s system of equations, recalled below, to waves equation [2.43]:
[2.44] 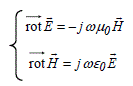
By using the Laplacian formula in Cartesian coordinates, the solutions to the eigenvalues of wave equation [2.30] reach the wave numbers expressed in formula [2.45]. The wave numbers then constitutes a spectrum of numerical values attached to the three integer numbers m, n and p. The indices of the symbol k specify the sequencing of the modes. However, we need to mention further that for the planned use of the cavity, at least two integer numbers must be non-zero:
[2.45] 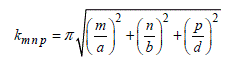
By making an analogy with a waveguide of the rectangular surface a x b, which is short-circuited at both ends in z = 0 and z = d, the analytical solutions of the wave equation dissociate themselves in the TM and TE modes. For the first solutions designated by the symbol TMm n p, the magnetic field vector ![]() has two components Hx and Hy, whereas the vector
has two components Hx and Hy, whereas the vector ![]() the electric field has three components Ex, Ey and Ez. The resolution of the wave equation leads to the following expressions [BLA 85, COL 61, HAR 60, LIU 83, ROU 65]:
the electric field has three components Ex, Ey and Ez. The resolution of the wave equation leads to the following expressions [BLA 85, COL 61, HAR 60, LIU 83, ROU 65]:
[2.46] 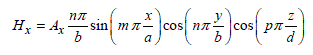
[2.47] 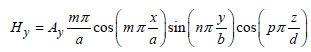
[2.48] 
[2.49] ![]()
[2.50] ![]()
Let us specify that among the set of coefficients A and B, only one is unknown. The others are deduced thanks to the properties of Maxwell’s equations. The k parameter is the wave number calculated for the propagation in free space and is at the right of equation [2.43].
The electric transverse modes identified by the symbol TEm n p constitute the dual form of the TM modes, for which the electric field vector ![]() only has two components depending on the ox and oy axes. The magnetic field vector
only has two components depending on the ox and oy axes. The magnetic field vector ![]() has three components.
has three components.
The formulas associated with the TEm n p modes are developed below:
[2.51] 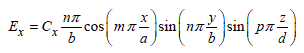
[2.52] ![]()
[2.53] 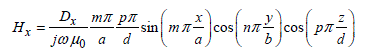
[2.54] 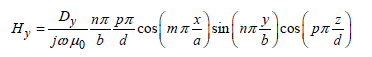
[2.55] 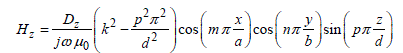
The C and D coefficients also obey the properties mentioned for the TM modes.
2.3.3. The first eigenmode
We can link the wave numbers coming from relation [2.45] to eigenfrequencies designated by the symbol fn m p and directly converted in expression [2.56] below:
[2.56] ![]()
To explore the analogy with the 1D cavity studied in the previous section, an empty chamber excited on an eigenfrequency should thus produce an electromagnetic field of infinite amplitude. Indeed, the installation of an antenna in the chamber leads to a radiation. The successive reflections of this radiation on the metal walls enter simultaneously, as soon as the frequency of the sine wave source connected to the antenna rigorously tunes with an eigenmode. Without energy dissipation, the reflected fields are added without any amplitude reduction other than the dispersion. This is thus not surprising after an infinitely long time to find a field of infinite amplitude!
The first eigenmode, also called fundamental mode, is determined by the allocation of indices giving the eigenmode the lowest frequency and giving itself a non-zero field. Thus, for a chamber whose dimensions take the numerical data a = 1.9 m, b = 2.5 m and d = 2.8 m, this condition is carried out for m = 0, n = 1 and p = 1, i.e. a first eigenmode located on the 80.4 MHz frequency.
The ten formulas [2.46] to [2.55] recounting the projections of the vectors ![]() and
and ![]() respectively attached to the TE and TM modes, indicate that the zero value allocated to the m index vanishes TM modes. Thus, the first eigenmode can only receive the TE011 configuration. From the previous relations, we find a single component of the electric field directed according to the ox axis and two magnetic components projected on the oy and oz axes.
respectively attached to the TE and TM modes, indicate that the zero value allocated to the m index vanishes TM modes. Thus, the first eigenmode can only receive the TE011 configuration. From the previous relations, we find a single component of the electric field directed according to the ox axis and two magnetic components projected on the oy and oz axes.
Knowing that the frequencies involved in the use of the reverberation chambers are generally located above 100 MHz, it is easier to carry out the electric field measurements. We will thus pay more attention to the expression of Ex specified below:
[2.57a] 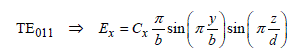
We must mention that this expression is dependent on the implicit condition set by the dimensional ratios a, b, d for these chamber dimensions i.e.:
[2.57b] ![]()
The examination of this formula shows that the electric field is invariant according to the ox direction and that it has a maximum amplitude at the center on the lines of coordinates y = b/2 and z = d/2. Figure 2.8 shows the amplitude distribution of the component Ex in a plane parallel to the oxz graph and located at the y = b/2 coordinate. On the right side of the figure, the field distribution is found in a plane parallel to the oxy graph and going through the coordinate z = d/2.
Figure 2.8. Distribution of the electric field in the fundamental mode
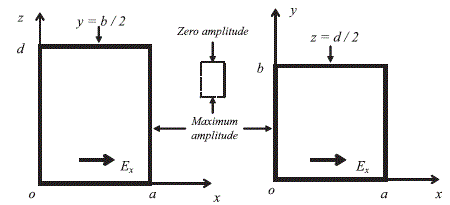
Even if the functioning in the fundamental mode turns out to be unusable for the applications mentioned in this book, the examination in Figure 2.8 will facilitate the understanding of mode stirring discussed in section 2.4.2 of this chapter.
2.3.4. Higher order modes
As soon as we allocate three non-zero values to the m, n, and p indices, relations [2.46] to [2.55] indicate the simultaneous presence of the TE and TM modes, exactly matching on fm n p. These configurations cover three electric field components and three magnetic field components.
From the practical point of view, this means that an object immersed in the chamber should be impacted by fields under an almost isotropic polarization and with the assumption that the TE and TM modes have identical amplitudes. To illustrate this feature, the analysis will be eased by taking a look at the particular case of the symmetrical modes with three identical non-zero indices.
For the unit indices and for the previously chosen dimensions of the rectangular cavity, the frequency of the first symmetrical mode takes the value f111 = 112 MHz.
Relations [2.51] and [2.55] show that the TE111 mode are associated with the loci of maximum and minimum amplitudes of the Ex component located at the center of two opposite walls of the chamber. Thus, the maximum amplitude appears on the wall containing the oyz graph, whereas the minimum amplitude concerns the opposite wall. Conversely, the Ey component will produce these properties at the center of the wall merged with the oxz graph and on the opposite face. Concerning the TM111 mode, equation [2.50] confirms the rotation of the symmetry, since the extreme values of Ez will be referenced on the oxy graph. Figure 2.9 gives a graphical representation of the phase opposition of the maximum and minimum electric field components, which are normal at the concerned walls. The dark stains represent the amplitude extremes. The diagram on the right of the figure gives the amplitude scale adopted in the AA’B’B plane parallel to the oxz graph and going through the coordinate y = b/2.
Figure 2.9. Amplitude variations of the Ez component attached to the TM111 mode
If we increase the order of the modes with the condition that the indices m, n and p remain identical, we go to a periodical distribution of the field. Thus, for indices all taking 3 as a value, the frequency of the mode goes to f333 = 336 MHz. Figure 2.10 gives, with the conventions previously adopted, the periodical distribution of the amplitude of Ez found in the AA’B’B plane and in the plane orthogonal to the previous plane located on the right side of the figure.
In this rectangular cavity excited at a frequency of 336 MHz, the field will thus be made up of the juxtaposition of 27 modal cells. The shape of each cell field pattern is strictly similar to the cell observed at the 112 MHz frequency.
Figure 2.10. Distribution of the modal cells of the TM333
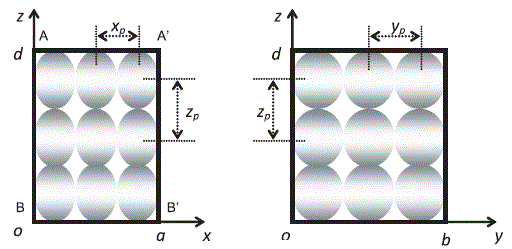
The xp, yp and zp repetition period in the space of the TM333 modal cells is strictly equal to 1/3 of the dimension of the chamber projected on each axis of the oxyz graph. On the other hand, it is interesting to compare this period to the wavelength calculated at the 336 MHz frequency, i.e. λ = 0.89 m. Indeed, a return on the chamber dimensions defined above shows that in the order indicated in expression [2.58], the respective components of the period take as numerical values 0.63 m, 0.83 m and then 0.93 m, i.e. orders of magnitude similar to λ:
[2.58] ![]()
By relying on this example, we will say that a cavity which is oversized compared to the wavelength must function under model periods of values much lower than the dimensions a, b and d. At the 336 MHz frequency and for the chamber considered in this text, this condition is thus not quite satisfying. However, to excite the cavity on the TM999 mode, the frequency must go to f999, i.e. practically 1 GHz. This corresponds to a wavelength of 30 cm, i.e. almost 9 times lower than the dimensions of the chamber. At the frequency of 1 GHz and above, the chamber in question will be fully oversized.
2.3.5. Mode spacing and mode density
The mode spacing is related with their distribution as a function of the frequency. Let us come back to expression [2.56] containing the eigenfrequency of the mode of any index m, n, p. To simplify the analysis, let us take a look at the particular case of a symmetric mode with three identical indices, i.e. m = n = p = q. With the help of this relation, we can determine the eigenfrequency of one of the three modes immediately higher than fq q q, i.e. for the considered example fqqq+1. Equation [2.59] gives the corresponding analytical expression:
[2.59] 
By making the hypothesis that the q index is much higher than one, formula [2.59] can be simplified to the advantage of its second-order series expansion [2.60]:
[2.60] ![]()
The Δf parameter then represents the spacing of these two consecutive modes. We then realize that the analytical formula [2.61] deduced from this transformation leads to a result proving that Δf is independent of the q index, i.e.:
[2.61] 
This fact does not contradict the study of the 1D cavity described in the previous section. Indeed, we reach expression [2.14] where the spacing of two consecutive modes of the 1D cavity is indeed a quantity inversely proportional to the L0 dimension and independent of the n order of the modes. For a 3D cavity, things are however more complex. Let us not forget that relations [2.60] and [2.61] have been established with the hypothesis of a q index much higher than one. That necessarily supposes that the cavity is highly oversized compared to the wavelength. Moreover, in the Δf gap, other modes come to insert themselves. They come from other combinations of indices m, n and p that are presently omitted. To illustrate mode insertion, we carried out the calculation of expression [2.56], determining the position of the modes contained between the 900 MHz and 920 MHz frequencies and for the reference chamber whose dimensions are recalled in a block in Figure 2.11. The position of each mode is marked by a vertical line.
Figure 2.11. Positions of the modes between 900 MHz and 920 MHz according to [2.56]
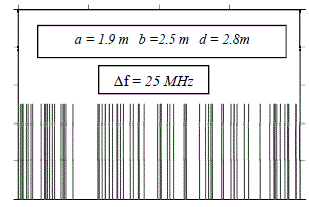
We can see that the approximate calculation carried out by expression [2.61] leads to a Δf spacing close to 25 MHz, whereas between 900 MHz and 920 MHz, we can note about 60 modes on the exact calculation projected in Figure 2.11.
In the Δf frequency gap, we can thus talk about a density of modes whose value will only increase with the oversizing criterion. The symmetry conditions also affect the mode density. Thus, for a chamber with a rigorously cubic shape and a volume similar to the one previously described, we would count only 8 modes between 900 MHz and 920 MHz. Increasing the modes density with the frequency is a major difference with the behavior of the 1D cavity studied in the first section of this chapter. The demonstration leading to the drawing of Figure 2.11 proves that the numerical calculation alone of the modal frequencies helps to rigorously set the density for a frequency f0 of a previously determined excitation.
However, following the works of the German mathematician Hermann Weyl, one was able to carry out the asymptotic calculation of the eigenvalues distribution of some differential operators. From the Laplacian analysis of the rectangular cavity, we then reach an analytical formula linking the number of modes N to the excitation frequency f0 of the cavity. The obtained expression, called Weyl’s formula is recalled below [LIU 83]:
[2.62] ![]()
Let us specify that we reach the same formula by assuming the analogy with the filling of the cavity by a photon gas with a very small wavelength [LAN 67].
It is thus easy to extract from this formula the modes density function, designated by the symbol D(f0). This function is related to the ΔN modes entering a narrow frequency band Δf0, centered on f0, i.e. the ratio ΔN/Δf0,
Consequently, when Δf0 tends towards zero, D(f0) converges on the first derivative of Weyl’s formula:
[2.63] 
Examination of the formula recounting D(f0) shows that the physical unit of the modes density is expressed in Hz-1. This function follows a law proportional to the square of the frequency.
2.3.6. Quality factor of the 3D cavity
As mentioned in section.3.3, an empty cavity excited under an eigenmode, but made up of perfectly electrically conducting walls, enters in resonance, in order to produce a field of infinite amplitude. We then find a rigorous analogy with the 1D model described in section 2.2.3. Indeed, as with any perfect resonant cavity submitted to a sinusoidal wave at t = 0, the peak-to-peak amplitude of the field or collected voltage on a sensor designated by the Amaxi(t) function, will indefinitely increase with a law proportional to the time. If we now take into account the thermal losses in the walls, the field or voltage mentioned above behave according to expression [2.64]:
[2.64] 
where the parameter τ represents the time constant of the resonant cavity and γ(t) represents the step function, meaning that for times prior to zero, the field or voltage are necessarily zero. For an infinitly long time, expression [2.64] tends to the steady state amplitude A0. Strictly speaking, expression [2.64] only represents the resulting field, including the multiple reflection cycles of the waves on metal walls of the chamber. Knowing that every reflection is damped by the losses, we witness a step by step reduction of the resulting amplitude which leads to a standing wave. Function [2.64] then illustrates this process in a simple way exploring the analogy with the theory of resonant electric circuits. Consequently, this formula is only valid if the ![]() time constant is much higher than the period of successive reflections.
time constant is much higher than the period of successive reflections.
In other words, the steady state of the cavity amounts to saying that the power produced by the transmitting antenna exactly balances the thermal energy losses in conductive walls. Moreover, we will store in the volume of the cavity balanced magnetic energy WM and electric energy WE. The electromagnetic energy thus stored will be independently calculated by the integrals of the square amplitudes of the magnetic field ![]() and the electric field
and the electric field ![]() vectors, extended to the volume V the cavity. The expressions in [2.65] reproduce these integrals, where the vectors
vectors, extended to the volume V the cavity. The expressions in [2.65] reproduce these integrals, where the vectors ![]() and
and ![]() are related to the peak amplitudes of the fields under harmonic variations [STR 69]:
are related to the peak amplitudes of the fields under harmonic variations [STR 69]:
[2.65] 
If Pd represents the power losses in the cavity walls, we propose extending formula [2.31] of the Q factor for a1D cavity to the case of a 3D cavity. We reach expression [2.66], in which the use of the notation Qm n p is aimed at the quality factor of the rectangular cavity, operating at the eigenmode with angular frequency ωm n p:
[2.66] 
Analytical calculation of the quality factor of the rectangular cavity leads to two formulas, depending on whether the field comes from the TE or TM modes. We will give the rigorous expression found by B.H. Liu et al. for the TEm n p mode [LIU 83]:
[2.67] 
In this formula, Zw represents the impedance of the plane wave in the vacuum and Rs is the surface resistance of the walls of an electric conductivity σ. These parameters take as expressions:
[2.68] 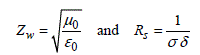
Let us note that in the presence of walls made up of a ferromagnetic material (such as the steel of relative magnetic permeability μr), the δ skin depth, located at the denominator of [2.68], takes the value:
[2.69] 
The kx, ky, kz and kxy coefficients, present in the expression of Qm n p, are connected to the components of the eigenwave number vector [2.56] by putting the conventions [2.70]:
[2.70] ![]()
The formula of the quality factor of the TMm n p modes can be found in Appendix 2.
Although rigorous, expressions [2.67] and [A2.1] are not very easy to use. Moreover, when the cavity becomes oversized compared to the wavelength, it is better to use an average quality factor. This factor is the result of the calculation of Q in a narrow frequency band Δf0, centered on the excitation frequency f0 of the cavity. As previously mentioned, Liu et al. have managed to reach the simplified relation [2.71], in which there is only the skin depth δ, the volume of the cavity V and the surface S of the walls:
[2.71] ![]()
This formula is based on the hypothesis of the modal density, which is itself based on Weyl’s law. It is however only valid for a really oversized chamber. The use of the approximate formula [A2.14], established in Appendix 2, allows us to link a corrective term to the simplified expression [2.71].
Let us take a more particular look at formula [2.64], expressing the end of the transient state. This relation can be found again by forming the analogy between the cavity and a set of resonators. We thus extend to the 3D cavity, the reasoning used in section 2.2.4. However, compared to the 1D cavity excited by a current source, we will see later on that the energy sent in the chamber, is obtained thanks to a transmitting antenna. The electromagnetic coupling of this antenna occurs in the series combination of the c0 capacitance and the l0 inductance. Let us recall that these two parameters are mentioned in the dotted rectangle in Figure 2.4. The comparison to electric circuits has the advantage of more directly establishing the connection between the τ time constant present in [2.64], and the Qm n p quality factor of the excited mode, i.e.:
[2.72] ![]()
Let us recall that the use of this relation is however subjected to the fact that the period of the numerous reflections of the waves in the chamber remains much shorter than τm n p. If these conditions are met, relation [2.72] can be extended to an oversized cavity and consecutively to the average quality factor set out in expression [2.71]. We will see in section 4.4.4 that the measurement of τ is possible, in order to obtain from expression [2.72] a value of the quality factor of the chamber.
In this context, the confined radiation of an antenna installed in a reverberation chamber is carried out by a process of power transmission. Chapter 3, section 3.5 and Chapter 6 bring more details about this process. With this physical analysis, a radiated power Ptr results from the transmission antenna. All of this power will be dissipated under the thermal form in the metal walls of the chamber empty of any other object but the transmission antenna. The balance between the incoming power and losses in the cavity is related in equation [2.73], where Pd corresponds to the power losses in the walls:
[2.70] ![]()
According to the definition of the quality factor stated by equation [2.66] it appears that the knowledge of the Q factor, combined with the power radiated by the antenna, helps to reach the electric energy WE. This energy is stored in the chamber under this operating mode. From [2.65], we know that WE is determined by the integral in the chamber volume of the square amplitude of the electric field vector. For an empty and perfect rectangular chamber, the electric field answers to analytical expressions [2.46] to [2.55]. Determination of the integral of the relations is immediate. It is thus easy to calculate the maximum amplitude of the electric field generated in the chamber. This parameter will be essential later on, since it will enable us to estimate the constraint undergone by the objects submitted to electromagnetic immunity tests.
Let us apply the reasoning to the case of a chamber excited in the first eigenmode. Depending on the geometrical parameters used in section 2.3.3, we obtain for the TE011 first eigenmode, the component of the electric field Ex with respect to the oxyz coordinate system in Figure 2.8. Ex is expressed by relation [2.57] recalled below:
[2.74] 
In this formula, the Em parameter indicates the maximum amplitude of the continuous sinusoidal waveform at the frequency f0. From the integral [2.65], we easily find the WE electric energy stored in the cavity, i.e.:
[2.75] ![]()
The combination of relations [2.66] and [2.75] leads to the maximum amplitude of the electric field produced on the first eigenmode. This expression then contains the Ptr power sent by the transmitting antenna:
[2.76] 
The fundamental mode of the chamber is located at 80.4 MHz and has a volume close to 14 m3. If we suppose at this frequency that the quality factor due to the walls is close to 105, a transmitted power in the room of 100 mW produces, according to [2.76], an electric field Em with an amplitude close to 1 kV/m. We will see in Chapter 4 that the objects immerged in the chamber lead to the reduction of the Q factor, in a ratio that can reach a factor of 10. However, the method remains very attractive for generating high amplitude fields with a low level of transmitting power in the room.
As seen in section 2.2.6 during the analysis of the 1D cavity made up of a coaxial line, the ability to couple the energy in an eigenmode was dependent on the position of the current source. This context can be transposed to the case of an antenna located in a 1D cavity, made up of two parallel reflective planes.
2.3.7. Regarding the excitation conditions of the cavity
For the requirements of the analysis, the considered 1D model will be a Fabry-Perot cavity, made up of two planes, whose ideally reflecting surfaces are distant from and parallel to L0, as specified by Figure 2.12. On the oz axis, normally arranged at the two planes, we can see a plane wave propagating. Its electric field vector ![]() parallel to the mirrors is directed according to the choice defined in Figure 2.12. The magnetic field vector, marked by the arrow, is normal to the electric field vector. The reflector, merged with the origin of the oz axis has the index 1, whereas the opposite reflector, receives the index 2.
parallel to the mirrors is directed according to the choice defined in Figure 2.12. The magnetic field vector, marked by the arrow, is normal to the electric field vector. The reflector, merged with the origin of the oz axis has the index 1, whereas the opposite reflector, receives the index 2.
Figure 2.12. Wave maintained in a Fabry-Perot cavity

The analogy with the 1D coaxial cavity of the previous section leads to the allocation to the electric field vector of the E(z) function, expressed in relation [2.77]. A and B are two unknown constants associated with the forward and backward travelling waves, both maintained between the two planes. For now, we do not formulate hypotheses on the excitation conditions of this standing wave:
[2.77] ![]()
If they are high conductivity metal walls, the ![]() electric field vector vanishes on the surface of each reflector, i.e. in z = 0 and z = L0. From this assessment, we can see that the A and B constants entering function [2.77] will be the solutions of an undetermined linear system. The way to handle this situation is then strictly similar to the developments used in section 2.2.3. It results from the calculation, the installation of the eigenmodes, with which kn the wave numbers specified in relation [2.78] are associated:
electric field vector vanishes on the surface of each reflector, i.e. in z = 0 and z = L0. From this assessment, we can see that the A and B constants entering function [2.77] will be the solutions of an undetermined linear system. The way to handle this situation is then strictly similar to the developments used in section 2.2.3. It results from the calculation, the installation of the eigenmodes, with which kn the wave numbers specified in relation [2.78] are associated:
[2.78] ![]()
To more accurately analyze the source coupling at the standing wave maintained in the Fabry-Perot cavity, we will first forget reflector 2. We place an electric dipole of ΔL dimension at the point of coordinate d positioned on the oz axis in Figure 2.13. In Appendix 5 the reader can find a detailed description of the formulas of the electric dipole.
Figure 2.13. Coupling of an electric dipole with reflector 1
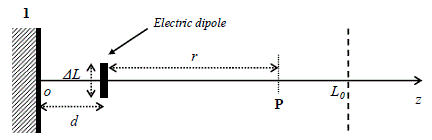
The dipole is directed in parallel to the electric field carried by the standing wave generated in the cavity. An observer P, positioned on the oz axis is located between the dipole and the L0 coordinate, showing (by a dotted line) the mark of reflector 2. The distance between the dipole and the observer is represented by the symbol r. With the assumption that r is comparable to or higher than the wavelength λ, the field produced by the dipole at point P will be expressed thanks to the far fields formulas. According to the theory of electric images, we show that the Er resulting field at point P is the algebraic sum of the two complex quantities of equation [2.79]. This equation contains an amplitude constant C, as well as the wave number k in free space. The use of the far-field electric dipole formulas is not incompatible with the 1D cavity model, currently used. Indeed, the 1D model of the Fabry-Perot cavity comes from the infinite flat shape of the mirrors. Therefore, the use of the electric images theory helps to adapt the dipole formulas with the simplified representation of the cavity:
[2.79] ![]()
The first term of this expression represents the direct dipole field, and the second term is the field produced by its electric image. Depending on the position d of the dipole, brought back to the reflective plane, the observer is thus submitted to constructive or destructive interferences that significantly contribute to the amount of energy that fills in the cavity. For the needs of the demonstration, the resulting field will be presented in the form [2.80], which is more appropriate to this context:
[2.80] 
This relation clearly shows that the interference will be constructive if we locate the dipole at such a distance from the reflector, that at the considered frequency, the exponential function in brackets takes the value -1.
This leads to writing the condition mentioned in equation [2.81]:
[2.81] ![]()
It now remains to interpret this result in the presence of the second reflector. We know that to make the cavity enter resonance, the wave number must be quantified depending on relation [2.78].
Consequently, it is sufficient to insert kn into equation [2.81], in order to show that the maximum amplitude of the eigenmode of index n, excited in the cavity, will be reached when dp takes the values satisfying equation [2.82]:
[2.82] ![]()
Knowing that the backward wave contained in [2.77] has an amplitude that is in strict opposition to the forward wave, the electric field on an eigenmode of resonance is described by the sinusoidal standing wave of E0 amplitude, formulated in [2.83]:
[2.83] ![]()
This expression indicates very well that, by positioning the dipole at the points of coordinates dp defined in [2.82], there is a rigorous coincidence with the extreme values of the sine function. This condition means that the Fabry-Perot cavity is excited in an optimal way. The alternative approach, established by taking the dipole image brought back to reflector 2, leads to a similar conclusion.
Conversely, if we seek the positions allocating a destructive composition to the dipole-image interference, it comes down to choosing, for the distance d from the reflector, the condition mentioned in equation [2.84] is achieved by a line of reasoning parallel to that which was previously used:
[2.84] ![]()
Tuned on an eigenmode, this position just coincides with the zeros of the previous sine function. Then this result proves that these positions can only produce interferences generating opposite couplings.
Another approach consists of looking at the impedance properties of the standing wave generated in the Fabry-Perot cavity. In order to do this, we determine the magnetic field whose solution taken from [2.77] takes the form [2.85], in which appears the impedance of the plane wave Zw:
[2.85] 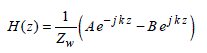
By taking into account the boundary conditions at the mirror planes, considered as perfectly electrically conducting materials, we reach the impedance expression of the standing wave Zst(z), i.e.:
[2.86] ![]()
This formula shows that for the z positions occupying the extreme amplitudes of the electric field, the impedance of the standing wave is infinite. This is strictly equivalent for the transmitting antenna to an optimal power injection in the space. When we place ourselves on a zero field, the standing wave impedance predicted by [2.86] is strictly zero. This is similar to placing a short-circuit on the transmitting antenna.
For the 3D cavity, the examination of relationships [2.46] to [2.55] describing the electric fields distribution in an empty rectangular cavity, leads us to quote similar conclusions. To found the conditions leading the maximum level of energy on the first eigenmode, it is sufficient to analyze the standing wave field pattern shown in Figure 2.8. Excited by an electric dipole type, the latter must be directed according to the polarization of the electric field Ex supported by this specific mode. On the other hand, the layout of functions [2.57] or [2.74] shows that the electric field records extreme amplitudes and consecutively an infinite impedance of the standing wave on a line passing through the centers of the walls perpendicular to the horizontal ox axis. Let us specify that a displacement of the dipole depending on the ox direction does not alter the coupling intensity.
However, to inject the optimal energy on the TM333 mode, whose electric field pattern of component Ez is illustrated in Figure 2.10, the dipole can be directed perpendicularly to the upper and lower walls of the cavity and in a coordinate point distant from the origin of the coordinate system, located at a half period of the modal cell, i.e. xp/2 and yp/2. Any other point far from the previous by a multiple of the modal periods xp or yp, also satisfies the optimal coupling criterion. This condition is maintained during a translation of the antenna, carried out following the vertical oz axis and on points coinciding with a multiple of the zp modal period.
Strictly speaking, a dipole directed in accordance with the previous instructions can only generate a standing wave, whose electric field is polarized according to the oz direction. To simultaneously excite the other components, it is necessary to have two other polarized dipoles according to oy and ox. This can only be carried out thanks to a transmission antenna giving an isotropic polarization. We will see further on that any metallic and passive object diffracting the waves, leads to the distortion of the shape and of the distribution of the modal cells. Knowing that an antenna is necessarily made up of a more or less amount of high conductivity material, its presence imperatively acts on the local distribution of the field. This is the case in a proportion that a numerical calculation can rigorously predict. Intuitively, we can conclude that the optimal energy transfer in the chamber will be more or less influenced by the presence of the transmitting antenna.
If we carry out the analogy with the Fabry-Perot cavity, this comes to say that the presence of the dipole acts as an obstacle. And this with the effect of modifying the harmonic solutions of the field described by equations [2.77] and [2.85]. The distribution of the fields in the cavity will thus no longer be described by a single sinusoidal function, but by a series similar to expression [2.41], proposed during the study done on the coaxial cavity. The distortion, as small as it is, of the longitudinal field distribution will be accompanied by a deviation of the modal frequencies.
Moreover, and as mentioned above, the field amplitude maintained in the cavity excited on an eigenmode is strongly dependent on the extent of the thermal energy losses into the walls of the cavity. We can add to this phenomenon an additional loss of energy due to the ambient field that also couples to the transmitting antenna.
In other words, the presence of a transmitting antenna is a necessary piece of equipment for the chamber excitation. But this is also an absorbing element of the stored energy that inevitably leads to the reduction of the chamber quality factor. Any other object contained in the chamber will have a similar impact. It is necessary to study it carefully, in order to predict the waves’ amplitude, for the analysis of the mode stirring efficiency. Before crossing this essential step in the understanding of the behavior of mode-stirred cavities, we turn now to the concept of the plane wave spectrum.
2.3.8. Plane wave spectrum
We will see the usefulness of the plane wave spectrum during mode stirring simulation. The spectrum concerns the projection of the electromagnetic fields in the space related to the wave numbers. Contrary to the concepts introduced in Chapter 1, the plane waves examined in this section are mathematical functions resulting from a space transformation. The properties of the Fourier integrals help us to carry out this transformation. As a preliminary illustration, let us come back to the standing wave maintained in the Fabry-Perot cavity, described by relation [2.83].
If we indefinitely extend the computation domain of this function, the plane wave spectrum consists of determining the Fourier transformation, present on the right of equation [2.87]:
[2.87] ![]()
The spectral function, designated by the E symbol, naturally associated with this 1D model, will thus only depend on the kz variable which is similar to a wave number. The z index below the symbol k recalls that the calculation of the Fourier transformation concerns the z space variable, i.e.:
[2.88] 
According to the mathematical concept of distributions, we know that the sinusoidal function [2.87] has, as a spectrum, two shifted Dirac functions expressed under the notations of equation [2.89]:
[2.89] ![]()
From the phenomenological point of view, the sinusoidal function written in [2.87] amounts to the interference of a forward plane wave, which propagates in the direction of the oz axis, and of a backward wave, whose description is strictly the opposite of that previously described. Following this description, the first term of the right member of equation [2.89] represents the spectrum of the backward wave and the second is the spectrum of the forward wave.
The calculation can evidently be extended without any difficulty to a cavity with a rectangular form. For example, examination of formula [2.50] set out in section 2.3.2 relates to the Ez electric field component attached to the TM333 mode, taking as an expression:
[2.90] 
We then go to the plane wave spectrum of this function, by applying the Fourier 3D transformation, whose general formulation is stated below [HIL 98]:
[2.91] 
The integration domain D will be extended to the infinite set of possible values of the three space variables x, y, z.
Applied to expression [2.90], the Fourier 3D transformation comes down to produce three simple integrals that we will write under the following conventions:
[2.92] 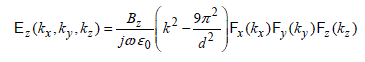
The Fx y z functions found in this relation specifies the spectra associated with each of the three space variables x, y or z:
[2.93a] ![]()
[2.93b] ![]()
[2.94] ![]()
Index 3 at the bottom of the wave numbers identifies the sequencing of the mode. For the TM333 considered here, the symmetry leads to: n = 3, m = 3 and p = 3, i.e.:
[2.95] ![]()
Projected in the space of the wave numbers, the particular values of the kx y z variable making the spectrum of the Ez component of TM333 different from zero, will be located on the eight summits of the parallelepiped in Figure 2.14.
Figure 2.14. Set of wave numbers that makes the E(kx, ky, kz) function non-zero
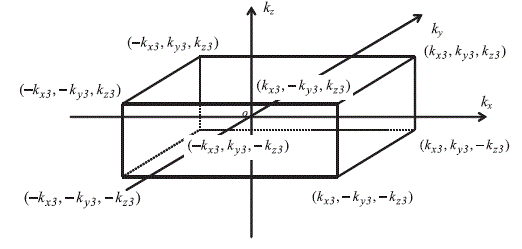
This representation immediately suggests adding the properties of a ![]() vector to the wave number. The components of this vector appear at each corner of the diagram in Figure 2.14, i.e.:
vector to the wave number. The components of this vector appear at each corner of the diagram in Figure 2.14, i.e.:
[2.96] ![]()
To describe the ![]() vector, we use three unit vectors
vector, we use three unit vectors ![]() , and
, and ![]() , which are common to both the spatial coordinates and the wave number spaces.
, which are common to both the spatial coordinates and the wave number spaces.
By using the same convention, the position of the observer will be expressed by the x, y, z coordinates, merged with the projections of the ![]() vector developed below:
vector developed below:
[2.97] ![]()
With the use of the vectors, the formulation of Fourier integral [2.91] can be radically simplified in order to only put in exponent the scalar product of ![]() and
and ![]() :
:
[2.98] 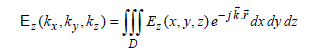
In the spirit of these new notations, the ![]() vector determines the propagation direction of the plane wave associated with it. According to the examination of the diagram in Figure 2.14, we can deduce that each corner of the diagram is a
vector determines the propagation direction of the plane wave associated with it. According to the examination of the diagram in Figure 2.14, we can deduce that each corner of the diagram is a ![]() vector, whose direction will depend on the sign exchange of the three components of the vector. Eight vectors thus result from it. They are supported by lines that have a common intersection point at the origin of the natural oxyz coordinate system.
vector, whose direction will depend on the sign exchange of the three components of the vector. Eight vectors thus result from it. They are supported by lines that have a common intersection point at the origin of the natural oxyz coordinate system.
We can associate with this mathematical representation the analogy with the interference of eight plane waves, carried by these lines, whose virtual generative sources would endlessly be rejected. This amounts to saying that the standing wave produced by the TM333 mode results from the interference of these eight virtual waves.
We will see that the reduction of the resulting field at this interference mechanism facilitates the simulation of some physical phenomena observed in a reverberation chamber.
2.3.9. Influence of the energy losses on the plane wave spectrum
It was shown in section 2.2.4 of this chapter that a 1D cavity excited on a mode was similar to an infinite number of resonators, made up of an inductance, a capacitance and a conductance, all connected in parallel. Such a simplified point of view suggests that the excited mode has a transfer function similar to a circuit with a very narrow bandwidth. Consequently, we may allow for the resonator attached to the mode of index n, the bandwidth Δfn., This bandwidth range depends on the quality factor Qn of the circuit and on the frequency f n of the considered mode n, i.e.:
[2.99] 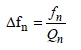
The resonator construction can be extended to a rectangular cavity, which behaves however differently from the 1D cavity. If we refer to the graph in Figure 2.11 and to the simplified expression [2.63] describing the modal density, we can say that an oversized cavity excited on a modal frequency includes a significant number of modes. These modes are inserted in the Δfn frequency band deduced from expression [2.99]. The analogy with the electric circuit involves that the contribution to the energy losses leads to the excitation of the resonators neighboring element n. Of course, if the excitation frequency f0 is rigorously tuned on fn, this mode has a predominant intensity when facing adjacent modes.
Converted in the writing conventions used for the 3D cavity, relation [2.99] takes the expression:
[2.100] 
We find again in this formula the average quality factor ![]() defined in [2.71]. The cavity excited on the fmnp frequency attached to the mode m, n, p, will thus produce other modes entering in the Δfmnp band. The level in the contribution of the adjacent modes will thus depend on their location with regards to the excitation frequency, but also on the coupling condition given by the transmitting antenna. Under such operating conditions, the field distribution in the 3D cavity will be the result of the interference of many standing sinusoidal waves, whose periods are not necessarily in harmonic ratios. This means that if the amplitude of the m, n, p, mode is predominant, the field pattern in the cavity will be organized by the composition of the modal cells, whose periods come from formulas [2.46] to [2.55] of the purely rectangular cavity. The periods are not in harmonic ratio and thus the resulting field will move away from the rigorously periodical model, shown in Figure 2.10; this means that some cells will be hotter than others. Moreover, if we move the transmitting antenna by maintaining an unchanged source frequency, it sometimes occurs that the antenna is located in such a way that the field of the m, n, p mode locally vanishes. In this case, the coupling of the energy on this mode will be reduced to the advantage of the adjacent modes. This phenomenon will be accompanied by a modification of the field distribution in the cavity, whose specific evaluation starts to avoid deterministic predictions. Thus, we have just described the embryonic stage of mode stirring [HOE 01].
defined in [2.71]. The cavity excited on the fmnp frequency attached to the mode m, n, p, will thus produce other modes entering in the Δfmnp band. The level in the contribution of the adjacent modes will thus depend on their location with regards to the excitation frequency, but also on the coupling condition given by the transmitting antenna. Under such operating conditions, the field distribution in the 3D cavity will be the result of the interference of many standing sinusoidal waves, whose periods are not necessarily in harmonic ratios. This means that if the amplitude of the m, n, p, mode is predominant, the field pattern in the cavity will be organized by the composition of the modal cells, whose periods come from formulas [2.46] to [2.55] of the purely rectangular cavity. The periods are not in harmonic ratio and thus the resulting field will move away from the rigorously periodical model, shown in Figure 2.10; this means that some cells will be hotter than others. Moreover, if we move the transmitting antenna by maintaining an unchanged source frequency, it sometimes occurs that the antenna is located in such a way that the field of the m, n, p mode locally vanishes. In this case, the coupling of the energy on this mode will be reduced to the advantage of the adjacent modes. This phenomenon will be accompanied by a modification of the field distribution in the cavity, whose specific evaluation starts to avoid deterministic predictions. Thus, we have just described the embryonic stage of mode stirring [HOE 01].
Before crossing this decisive step of the functioning of the MSRC, let us come back to the plane wave spectrum and more specifically to the graph in Figure 2.14. If we now take into account the population of the modes excited in the Δfmnp band, the impact in the space of the wave numbers will result in the addition of N0 sets of eight plane waves, whose incidence angles will depend on the projections of the ![]() vector, associated with the N0 modes entering Δfmnp. We will allocate to each of these waves, an amplitude coming from the spectrum evaluated from the Fourier transformation applied to the resulting field distribution in the cavity. This transformation thus assumes that the distribution will be known beforehand. We will see in the next section that adding hypotheses borrowed from the probability theory helps us to simulate the field distribution, without exactly knowing the amplitude allocated to the plane wave spectrum.
vector, associated with the N0 modes entering Δfmnp. We will allocate to each of these waves, an amplitude coming from the spectrum evaluated from the Fourier transformation applied to the resulting field distribution in the cavity. This transformation thus assumes that the distribution will be known beforehand. We will see in the next section that adding hypotheses borrowed from the probability theory helps us to simulate the field distribution, without exactly knowing the amplitude allocated to the plane wave spectrum.
2.4. The 3D cavity operating in stirred modes
2.4.1. Role given to mode stirring
There was shown in the previous section a 3D cavity empty of all objects, but excited on the first eigenmode produces standing wave with a sinusoidal distribution of the electromagnetic field. When we increase the frequency to reach the oversized behavior, the contribution of the energy losses, involves the excitation of mode packets. This results from two phenomena: the growth of their population and the bandwidth imposed by the average quality factor of the chamber. Furthermore, we know that the electromagnetic field is located in periodically spaced out modal cells.
Under such conditions, effects of the interference mechanisms produced by the mode packets lead the distribution of the field magnitude in various cells to no longer become rigorously periodic. This seems to move the field distribution away from the perfect sinusoidal model found in a non-lossy cavity. If we make a short frequency excursion, the field dislocation will be accentuated. The same observation can be made after insertion of a metal object in the chamber or with a modification, as small as it is, of one of the dimensions. Identical phenomena are also noticed when we move the position of the transmitting antenna. Mode stirring consists of intervening in several ways on these parameters, in order to accentuate the field dislocation, so that the field pattern avoids any deterministic description. Under these conditions, the field amplitude in the cavity or the power collected on a receiving antenna installed in the chamber seems to obey to continuous random variables, to which we try to attach known probability distributions.
It will thus be possible to associate the field amplitude or the power captured in one point of the chamber with an average amplitude matched with a standard deviation, or in some cases a maximum amplitude. The installation of a mode stirred reverberation chamber, able to carry out reproducible tests, thus consists of determining a frequency range and a space within the room where the properties of these random variables remain stationary. This amounts to saying that their random properties appear independent of the geometrical parameters of the chamber, as well as of the contribution of the electronic equipment under test.
Four methods of mode stirring are currently used.
Mechanical stirring consists of installing in the chamber a device fitted with metal blades rotating by a motor external to the shielded enclosure. As a function of the stirred volume, the field distribution in the chamber will be more or less disturbed. As soon as the frequency is sufficient to admit that the wavelength becomes comparable or smaller than the dimensions of the metal blades, the field data captured in the chamber will almost certainly adopt the properties of a random variable.
Electronic mode stirring, also called frequency agitation, acts on the frequency of the source, connected on the transmitting antenna installed in the chamber. If f0 designates this frequency, the process consists of selecting packets of N other frequencies, located close to f0. Under the condition of the oversized cavity, we can show that the N data of the electric field thus collected behave as random variables.
It is important to specify that electronic and mechanical stirring can be judiciously combined, in order to increase the population of random variables collected during a test.
To conclude this section, let us note that some systems use alternatives to mechanical stirring.
Stirring by dimensional modulation of the chamber consists of triggering mode agitation by a small variation of the chamber dimensions. The dimensional excursion will be carried out thanks to walls made up of a wire mesh distorted by actuators controlled by the measurement protocol.
Stirring by commutation or mobility of transmitting antennas plays on the variability of the modal excitation level. The performances of the process depend on the relative position of the antenna compared to the extremes or to the zeros of field carried by the standing wave generated in the cavity.
The next section, devoted to the general description of mode stirring, will be more specifically focused on the mechanical stirring. This stirring nowadays seems to be the most frequently used in the test centers equipped with MSRC. The other mode stirring devices will be detailed in section 4.3 of Chapter 4.
2.4.2. Mechanical mode stirring
To illustrate the impact of mode stirring, let us imagine a metal blade stirrer installed under the ceiling of the chamber, initially presented in Figure 2.7. Figure 2.15 below gives a cutaway parallel to the system of the oxz axis and going through the median plane of coordinate y = b/2.
Figure 2.15. Localization of the mechanical mode stirrer
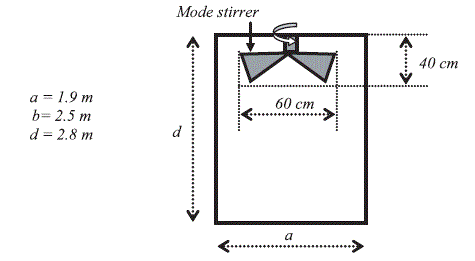
The a, b and d dimensions of the chamber are listed to the left of the figure. We will assume that the rotation of the stirrer covers a cylindrical volume with a diameter of 60 cm and height of 40 cm. This volume will later be referred to as the stirred volume.
In a first stage of the reasoning, we practice the analogy between the mode stirrer and the insertion of the obstacle at the point of coordinate zk of the coaxial cavity shown in Figure 2.5. Thinking again of this representation encourages us to simplify the problem even more by merging the obstacle with the localized capacitance, designated with the symbol Ck. We can easily show that the system described by equations [2.38] to [2.40] leads to the resolution of the transcendent equation below:
[2.101] ![]()
If the presence of the obstacle does not excessively disturb the eigenmodes of the empty cavity, the solutions of equation [2.101] will be designated by the kn’ coefficient made up of the algebraic sum of the initial kn wave number and of the unknown Δk term, to which the following model corresponds:
[2.102] 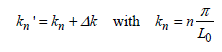
This fitting enables us to rewrite equation [2.101] in a form that is more tractable for the resolution and the physical interpretation, i.e.:
[2.103] ![]()
Angular frequencies and wave numbers entering this equation are linked to the propagation speed c of the TEM wave by [2.104]:
[2.104] ![]()
Assuming a little disturbance of this obstacle, the frequency shift of the eigenmode will be weak, then Δω and Δk remain absolute quantities much lower than ωn and kn, i.e.:
[2.105] ![]()
We can thus use the first terms of the series expansion of the sine function contained in equation [2.103] which takes the simplified form [2.106], where the computation of Δω and Δk becomes easy.
[2.106] 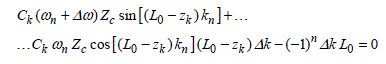
The insertion of the obstacle comparable to the Ck capacitance thus generates a deviation of the modal frequencies. Their excursion will depend on the n order of the mode and the zk coordinate. The example of the coaxial cavity indeed shows that the action on zk generates a basic mode stirring.
The analogy with the 1D cavity can be extended to the mode stirrer installed in the rectangular chamber in Figure 2.15. Indeed, the presence of the object made up of metal blades dramatically disturbs the electric field distribution. Under this geometric configuration, the solutions of the waves equation developed in section 2.3.2 for the empty cavity, must be revised, in order to exactly determine the km n p eigenmodes. Only the use of numerical calculation methods or experimentation can lead to the evaluation of the frequency deviation generated by the presence of the metal obstacle. The position of the mode stirrer will thus play a decisive role in the control of the mode shifting. If we examine first electric field distribution found on the first eigenmode, the illustration in Figure 2.8 shows that the mode stirrer located under the chamber ceiling will be in an electric field zone of low amplitude [ORJ 05].
The analogy with the 1D cavity and more especially the examination of equation [2.106] indicates that the argument contained in the sine and cosine functions will be a multiple of π, when zk coincides with a zero voltage. We immediately find that Δω will be zero. This confirms the intuitive reasoning.
We can thus conclude that an optimal mode excursion can only be carried out by installing the stirrer where the field given by the first eigenmode takes the maximum amplitude, i.e. at the center of the chamber. Such an arrangement has, however, the major drawback of occupying the working space!
We will see later on that for other reasons, the first eigenmode l is practically unusable. It is thus necessary to turn to modes of higher indices, such as the TM333 configuration in Figure 2.10. We realize that in such a case, the stirrer occupies the entire volume of the modal cell located at the summit of the chamber. The metal blades rotation thus has the effect of deeply modifying the local field distribution. The continuity conditions imposed on the boundaries of the modal cell make the field dislocation contaminate all the other cells. The very important disturbance of the field distribution is accompanied by a very significant shift of the eigenfrequency of the cavity.
Indeed, going back to the 1D model indicates that such a scenario introduces into the coaxial line in Figure 2.5 an obstacle whose longitudinal dimension is close to half a wavelength. Such a large scale alteration of the local geometry of the cavity will thus produce a very important deviation of the natural oscillations frequency, as well as a deep alteration of the longitudinal distribution of the currents and voltages.
Knowing that a 3D cavity leads to the theoretical modal distribution shown in Figure 2.11, the positions of these N modes will be modified by the rotation of the metal blades and materialized by distinct frequency deviations.
Moreover, we know that the energy losses produced in the walls of the chamber introduce modal interferences. These interferences contribute to the mixing of the standing waves. The composition of the waves is far from a perfect sinusoidal law.
These factors, added to the presence of the stirrer and to the many deviations of the eigenmodes frequencies, generate a field distribution avoiding rigorous deterministic predictions. The more the chamber becomes oversized compared to the wavelength, the more we increase the deviation of the modal frequencies.
2.4.3. Experimental proof of the modal excursion
Some results of experiments practiced on a reverberation chamber highlight the physical reality of the eigenmodes excursion, generated by the stirrer rotation.
The chamber corresponds to the geometrical parameters and to the mode stirrer shown in Figure 2.15. The transmission antenna is made up of a wire, located at about 15 cm from two metal walls adjoining the chamber. The reception antenna of identical constitution is located close to the walls opposite to the previous ones.
The advantage given by the concept of the transmission line mainly comes from the ability of such type of antennas to be matched on a very wide range of frequencies. Figure 2.16 brings some details on the arrangement of the antennas.
Knowing that the fundamental mode of the chamber is located at 80 MHz, measurements have been taken to cover the first eigenmodes located between 70 MHz and 130 MHz. The measurements have then been extended on two frequency bands of 20 MHz, respectively centered on 310 MHz and 910 MHz. This choice put the experiment in conditions of under and oversizing of the chamber.
Figure 2.16. Installation of the lines operating as transmitting and reception antennas

The layout in Figure 2.17 practiced at 70 MHz and 130 MHz show the variation of the power collected on the receiving antenna when we maintain the power invariant at the transmitting antenna. The vertical dotted lines give the location of the modes. These modes are calculated by formula [2.56] established on the assumption of the empty rectangular cavity.
We realize that the first maximum of the experimental curve exactly coincides with the empty chamber first eigenmode, located at 80.4 MHz.
However, as soon as we move away from the first eigenmode, we observe a more or less important gap with the modal frequencies predicted by the formula [2.56]. These conflicts bring concrete proof of the mode shifting generated by the electromagnetic coupling inside the room. This phenomenon is produced by the metal objects contained in the chamber, notably the presence of the mode stirrer. Indeed, each maximum indicates a resonance frequency that corresponds to its own excursion. We will notice that the amplitude of the maximums is different as a function of their position versus the frequency. This phenomenon is related to the level of modal excitation. A simplified explanation for this excitation level has been made in section 2.3.5.
Figure 2.17. Comparison of mode positions between 70 MHz and 130 MHz

In the second experiment practiced between 300 MHz and 320 MHz, the layout (continuous line in Figure 2.18) gives the power collected on the receiving antenna when we keep the mode stirrer motionless. The comparison of this curve with the position of the empty cavity modes shows that it is practically impossible to indentify the resonances stimulated during the experiment. The combination of three physical phenomena contributes to this behavior. With the increase of the frequency, we witness a growth of the mode density; the energy losses only widen the narrow frequency band and their coverings make them indistinguishable. To these primary mechanisms, we need to add the growing impact of the mode stirrer, whose size is getting close to the size of the modal cells.
These phenomena are even more amplified in Figure 2.19, devoted to the experiment carried out in oversized condition. The curve at the bottom of the graph has been recorded with the motionless mode stirrer. In order to amplify the disturbance generated by the modal excursions, we add on the first layout the maximum powers noted during a revolution of the mode stirrer. The obtained curve now has almost no connection with the previous curve. This experiment thus brings the proof of the random variations of the power received on the antenna. Let us point out that at a fixed frequency, the power received during a revolution of the mode stirrer generates a behavior just as unpredictable.
Figure 2.18. Comparison of mode positions between 300 MHz and 320 MHz
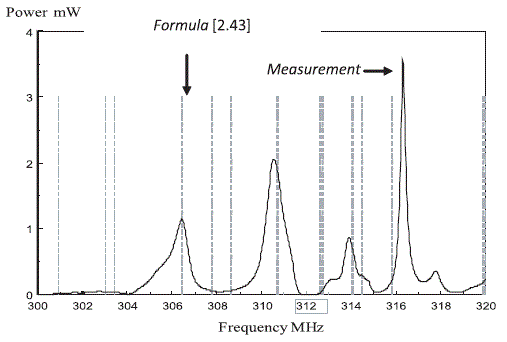
Figure 2.19. Comparison of the fixed and mobile stirrer layout positions

With the impossibility of describing these curves with the simple combination of analytical functions, we prefer to compare the power collected on the receiving antenna to a random variable. Knowing that the induced power comes from the standing waves, the concept of random variable can be extended to the electric and magnetic field variables. It is certain that at this complexity level, the analysis of the mode distribution is still the object of research studies [COZ 09].
2.5. Discussion
2.5.1. On the geometry of reverberation chambers
If the use of rectangular form chambers seems more rational with the prospect of easier insertion into the buildings, other geometrical structures are also possible.
Let us imagine a chamber with a circular ground floor, used in a similar way to the rectangular shaped room. The calculation would then highlight eigenmodes attached to indices organized in triplets of integers. The distribution of the eigenmodes versus frequency would then evidently be dependent on the analytical nature of the functions constituting every mode. In addition to the sine functions encountered for the parallelepiped we would find, for the cylindrical cavity, Bessel functions of the first kind. Their contribution should indeed have an impact on the mode distribution.
Considering the contrast of the dimensions, the impact will manifest itself with the appearance of mode packets. Let us consider the case of a skyscraper transformed in the reverberation chamber with a rectangular ground floor. The 1D model discussed in the first section of this chapter is indeed transposable to this case. Indeed, we are in the presence of a waveguide with short-circuited ends. With this analogy, as soon as we have gone through the cut-off frequency of the first guided mode, the cavity will behave strictly in the same way as the coaxial cavity by producing resonance frequencies periodically spaced out from the c/2L0 quantity, where c represents the celerity and L0 the height of the skyscraper. As soon as the cut of the second mode is made, a new resonance spectrum will appear and so on. Finally, the resonance distribution will be controlled by a series of periodical processes regulated by the emergence of the modes of the waveguide. A skyscraper with a cylindrical ground floor would not deeply change this behavior.
In the configuration of any other cavity made up of non-parallel walls breaking, as much as possible, the initial symmetry of the parallelepiped, the empty cavity would have resonances whose amplitude distribution would be far from the sine functions attached to the parallelepiped. It is plausible that such a geometry would anticipate the random behavior of the field distribution activated by mode stirring.
2.5.2. On the use of the RLC resonators
The comparison of a reverberation chamber to a network of RLC oscillators described in section 2.2.4 must take into account several conditions. To carry out this analogy, the Gn conductance brought back on each resonator must be low enough in order to preserve the assessment of the power losses in the cavity. The very subjective evaluation of this criterion can only be correctly established with the help of a preliminary estimate of the quality factor of the cavity excited on the resonance of n order. Moreover, it is necessary to know that the errors introduced by this simplified point of view are increased as soon as the modal interferences are involved. This is currently the case for cavities that are oversized compared to the wavelength.
The use of RLC resonators is particularly helpful to simulate the cavity in transient state. Knowing that this particular functioning results from the composition of successive reflections of the waves on the chamber walls, we should check if the approximate response of the resonators corresponds to the envelope of the effective transient response. With this purpose, we can find an advantage in investigating the first reflection episodes. The use of a model borrowed from the electric images theory can give interesting results. We know that the progress of the energy in the cavity is coordinated by the increase of clusters of images generating interferences. We can easily evaluate their resulting amplitude in preparation for such a confrontation [BAR 02].
2.5.3. On the contribution of the modal interferences
We know that for a cavity operating close to the first eigenmode the selection of a mode produces the analogy with the transfer function of a resonant circuit. If we modify the characteristics of the cavity by rotation of the mode stirrer, the tuning frequency of the mode involved will be altered in a proportion that only a theoretical simulation can predict with accuracy. Under these conditions, the field distribution carried out in the cavity can be expressed by a series constituted of terms composed of orthogonal functions. Except for cavities of simple geometrical forms (such as parallelepipeds or cylinders), the analytical description of the functions is almost impossible. If it is a parallelepiped containing a mode stirrer, we prefer to keep the sine and cosine functions coming from the calculation carried out with the empty cavity. Under this hypothesis and in the presence of a mode excited in the neighborhood of the first resonance frequency, the amplitude of the coefficients allocated to the functions will give a clearly marked maximum on the terms, whose indices are getting the closest to the excited mode resonance. Except for the tuning, the coefficients no longer respect this selection rule. Let us take a look at the functioning of a cavity that is oversized compared to the wavelength. The field description established on the sine functions always remains valid. The tuning of the cavity becomes highly plausible whatever the excitation frequency. Thus the amplitude allocated to the coefficients contained in the series has maximums for the indices giving eigenfrequencies close to the excitation frequency. The dispersion law of the coefficients is then controlled by modal interferences generated in the Δf0 bandwidth of the mainly excited mode.
Indeed, we have mentioned above that a mode excited on the f0 frequency amounts to a resonant circuit of Δf0 bandwidth. In this short frequency gap, much lower than f0, many other modes insert themselves, this phenomenon becomes more amplified as the cavity becomes oversized compared to the wavelength. The excitation level of the modes is evidently functions of the configuration of the transmitting antenna. Transported in the representation adopting the sine functions, the modal interferences will be similar to a group of sinusoidal standing waves, whose own periods are not in harmonic ratio. The amplitude allocated to the sine functions can only be determined after having knowledge of the field distribution thus excited. Thus, the theoretical simulation of the field remains possible at the cost of a very high requirement in numerical computation. It is mainly this difficulty that encourages us to choose random field distribution model. We will notice that the hypothesis does not contradict the composition of the interferences, whose resulting effect tends to behave as a random variable. Knowing that the mode stirrer rotation deeply renews the interferences, we can select NB positions of the stirrer restoring NB independent combinations of interferences.
From this qualitative description, it is practically admitted that the field distribution in an electromagnetic cavity, which is oversized compared to the wavelength, gets close to a stochastic process. The amplitude of voltages or of power collected on sensors or antennas installed in the chamber will thus be for these reasons comparable to a random variable.
2.6. Bibliography
[BAR 02] Baranowski S., Kone L., Démoulin B., “An optical approach to determine the statistical features of the field distribution in modes stirred reverberation chambers”, Ultrawideband Short Pulse 5, p. 555-560, Academic Press, New York, September 2002.
[BLA 85] Van Bladen J., Electromagnetic Fields, Springer Verlag, London, 1985.
[COL 61] Collin R.E., Field Theory of Guided Waves, McGraw-Hill, New York, 1961.
[COZ 09] Cozza A., “Statistics of the performance of time reversal in a Lossy reverberating medium”, Physical Review, E80, 056604, November 2009.
[DEM 03] Démoulin B., Enseignement Elémentaire sur la Propagation des Ondes, volume 1, course handout, Bachelor ESEA, Lille 1 University, September 2003.
[ELF 10] El Fellous K., Contribution à l’élaboration d’une méthode d’analyse reposant sur une approche “équivalent circuit” pour l’étude de la pénétration d’ondes électromagnétiques dans une cavité, Thesis, Limoges University, 2010.
[GRI 69] Grivet P., Physique des lignes de haute fréquence et d’ultra haute fréquence, volume 1, Masson, Paris, 1969.
[HAR 60] Harrington R.F., Time Harmonic Electromagnetic Fields, McGraw-Hill, New York, 1960. [HIL 98] Hill D.A., “Plane wave integral representation of fields in reverberation chambers”, IEEE Transactions on Electromagnetic Compatibility, vol. 40, no. 3, p. 209-217, August 1998.
[HOE 01] Hoeppe F., Analyse du comportement électromagnétique des chambres réverbérantes à brassage de modes par l’utilisation de simulation numériques, Thesis, Lille University, 2001.
[LAN 67] Landau L., Lifchitz E., Physique Statistique, Editions MIR, Moscow, 1967.
[LEM 09] Leman S., Démoulin B., Maurice O., Cauterman M., Hoffmann, P., “Use of the circuit approach to solve large EMC problems”, Comptes rendus de l’Académie des Sciences, vol. 10, booklet 1, p. 70-82, January-February 2009.
[LIU 83] Liu B.H., Chang D.C., Ma M.T., Eigenmodes and the composite quality factor of a reverberation chamber, NBS Technical notes 1066, August 1983.
[ORJ 05] Orjubin G., Modélisation modale d’une chambre réverbérante par la méthode des éléments finis: application à l’analyse paramétrique des tests statistiques, Thesis, Marne-la-Vallée University, 2005.
[RAG 48] RAGAN G.L., Microwave Transmission Circuits, McGraw-Hill, New York, 1948.
[ROU 65] ROUAULT M., Electricite, Fascicule II, Masson, Paris, 1965.
[STR 69] STRATTON .LA., Theorie de I 'electromagnetisme, Dunod, Paris, 1969.
