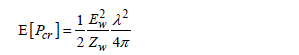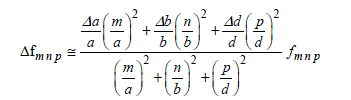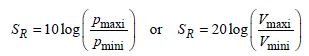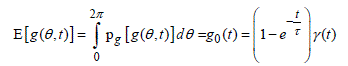Chapter 4
Impact of the Physical and Technological Parameters of a Reverberation Chamber
4.1. Introduction
This fourth chapter is mainly devoted to the characterization of the reverberation chambers. In order to test the ability of a chamber to produce an ideal random field, we will use the statistical concepts introduced in the previous chapter. The analysis will also be extended to the measurements of the quality factor.
Section 4.2 is devoted to the design parameters of a chamber. It takes a closer look at the impact of the factors that may influence several functional parameters, such as the position of the lowest usable frequency of the chamber or its composite quality factor. An important part of this section will be devoted to the correlation among the electromagnetic field data. Intuitively, we realize that two very close field samples do not form two rigorously independent variables. It will then be shown that the spatial correlation function of the field samples collected in an ideal reverberation chamber, takes the analytical form of a sine cardinal function. We manage to find from this result the correlation distance, closely related to the wavelength.
Section 4.3 discusses the main mode stirring techniques. Thus, we will examine the techniques of mechanical stirring, of frequency agitation and of changing position of the transmitting (or receiving) antenna.
Section 4.4 is subdivided into four sections. It first concerns the characterization of the efficiency of the mode stirring. Three criteria will be considered: the modal dislocation, the stirring ratio and the layout of the correlation function of the stirrer. The characterization of the chamber will be continued by the measurement of the stationarity of the stochastic field in the chamber. This part of section 4.4 is mainly devoted to the theoretical justification of the calibration procedure of the statistical uncertainty of the field amplitude. This calibration procedure is recommended by the international standards, which will be covered with amount of details in Chapter 5.
The methods for measuring the chamber’s quality factor are discussed in section 4.4.3. They concern three processes, whose physical principles will be very briefly described. The method of mode selection provides the analogy between the chamber and an RLC resonator, whose resonance frequency and bandwidth will be measured. The power balance method will be preferably applied when the room may be considered to be oversized. It consists of deducing the quality factor from the balance which is carried out between the injected power of a transmitting antenna and the collected power of a receiving antenna. The third method is based on the measurement of the rise time duration of the electromagnetic energy in the chamber to reach the steady state behavior. Knowing that this parameter is generally much higher than the average time slot between successive reflected waves from the chamber walls, we manage to find the quality factor from the theory of the resonant circuits.
The conclusion of section 4.4 tackles the question of the determination of a lowest usable frequency of the chamber. We know that the determination of this parameter is quite questionable since the lowest frequency marks the extremely fuzzy boundary located between the first eigenmode and the much higher frequencies giving the oversized condition. Therefore, the proposed method will remain an empirical characterization based on the calculation of the stirred volume and on measurements. They are both taken from the statistical properties of the data collected during a rotation of the mode stirrer.
4.2. Main parameters for reverberation chamber design
4.2.1. List of the main building parameters
The choice of a chamber, its installation or its construction is carried out as a function of geometrical or physical parameters. Their determination will be facilitated by consulting the theory of the electromagnetic cavities briefly presented in Chapter 2.
Generally, reverberation chambers will be made up of rectangular enclosures. This arrangement is very often enforced by the structure of the hosting buildings. However, it is quite possible to configure the chambers, whose walls are not necessarily parallel. In other cases, the chamber can be made up of an assembly of parallelepipeds with more or less contrast between volumes. To preserve the continuity with the previous chapters, the following text will only concern the rectangular shaped chambers.
The dimension parameters, i.e. length, width and height, will play a major role since they determine the frequency of the first eigenmode of the chamber and consequently the lowest usable frequency (LUF), which is also designated under the term, starting frequency. Whatever the terminology, we will adopt the fs symbol to designate this frequency. The technological criteria are added to the dimension parameters. The first criteria are mainly linked to the physical constitution of the walls, the access doors and the communication routes of the chamber with the outside environment. These technological factors mainly have an impact on the value of the quality factor. The mode stirring process is directly related to the performances of the tests carried out in the reverberation chamber. Its use aims at approaching the ideal statistical properties of the field distribution in the room.
Mechanical mode stirring requires the geometrical definition of a stirrer, made up of metal blades, whose design can have an important impact on the properties of the chamber. The physical principle of this method was tackled in Chapter 2. The mean used in order to move the stirrer is added to these technological criteria, depending on whether the rotation is carried out step by step or continuously. Other stirring modes can be used, independently or jointly with mechanical stirring. This is how we can practice the electronic stirring, also called “frequency agitation” or stirring by switching or moving the transmitting antennas. The characteristics of the mode stirrer, added to the geometrical characteristics of the chamber, as well as to the stirring process, will have an effect on the position of the lowest usable frequency of the chamber and on the random behavior of the data collected during an experiment or a test.
The following sections will be devoted to a more precise description of the impact of these parameters.
4.2.2. Impact of the geometrical and physical parameters of the chamber
Let us consider a chamber of rectangular shape with a, b and d dimensions. Linked to relationship [2.56] recalled below, the resonance frequencies or the eigenmodes of the empty chamber take the expression:
[4.1] 
In this formula, c is the celerity, i.e. the speed of light in vacuum, which is generally approximated by the numerical value of 3 108 m/s.
According to the developments made in section 2.3.3, the first eigenmode of the chamber leads to the choice of the m, n and p indices allocating to fm n p the lowest frequency able to make the cavity resonate. The sequencing of the m, n, p indices found in the first eigenmode will thus depend on the sides dimensions a, b and d. Equation [4.2] gives the calculation rule of the first eigenmode for the configuration shown on the left of the expression:
[4.2]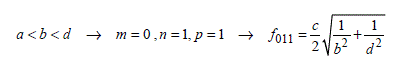 
However, the ideal random field distribution only appears under the condition of oversizing of the chamber compared to the wavelength. Thus, the lowest usable frequency fs will necessarily be much higher than the first eigenmode frequency. The ratio linking fs to the fundamental mode will mainly be dependent on the form and on the dimensions of the mode stirrer. Other factors also influence the lowest frequency, especially the presence of voluminous metallic evices. Generally, the experiment shows that fs is about five to six times higher than the first eigenmode, i.e. for the established example:
We can thus conclude that the lowest frequency of the chamber is lower when the volume of the chamber is large. To have a general idea of the orders of magnitude, a chamber of a volume of 15 m3 gives a lowest frequency close to 500 MHz and a chamber of 60 m3 leads to a frequency close to 200 MHz.
As shown in Figure 2.11, established in section 2.3.5, contrasts of side dimensions influence the mode distribution. Excessive ratio between a, b and d have the effect of producing groups of modes. A room that is too close to a cube shape involves a reduced mode density. In the preliminary stage of the construction of the chamber, a diagram similar to Figure 2.11 brings criteria, which are sufficient for the optimization of the choice of the dimensional features.
The building technology of the walls plays an important role. In general, we use wooden panels covered with plane metal sheets in galvanized steel. The panels are assembled with the help of metal gaskets, which are kept in contact with the two conductive faces, thanks to the pressure of a row of bolts. The access door of the chamber, as well as the various apertures communicating with the outside, strongly influences the properties. We pointed out in section 2.3.9 that the modal interferences strongly influenced the distribution of the ideal random field in the room. We know that these mechanisms mainly depend on the composite quality factor of the chamber. A high coefficient reduces the interferences and consequently plays against the random distribution of the field. Conversely, a low quality factor increases the direct coupling of the transmission or receiving antenna on the device under test. Looking for a compromise guided by the order of magnitude of the quality factor is thus essential to cover the expected properties of these chambers. Let us specify that it is almost impossible to establish a direct link between the electromagnetic leakages of a chamber and its performances in terms of the quality factor.
Indeed, the latter is above all dependent on various thermal energy losses, which occur in the chamber and its contents. For an empty chamber, the energy losses come from the surface resistance of the walls and from the dissipations produced on the contact resistances, which are caused by the gaskets. Specifically, the contact resistance at the perimeter of the access door, made as low and uniform as possible, also has a major contribution to the energy balance of the room.
We must add to these internal factors of the room itself, the energy losses due to the inductions on the energy supply cables. Such cables must be imperatively enclosed in a highly conducting tunnel, in order to avoid any direct electromagnetic coupling with the surrounding field.
If the impact of the quality factor affects the random field distribution and consecutively the efficiency of the mode stirring, this parameter influences dramatically the standing waves amplitude in the room and consequently the level of the field generated for susceptibility tests. As highlighted by the developments made in section 2.3.6 and leading to formula [2.76], the amplitude of the standing waves generated in the reverberation cavity evolves proportionally to the square root of the product of the power losses in the chamber and its quality factor. Moreover, this amplitude is also affected in an inversely proportional way to the square root of the excitation angular frequency ω0 and of the effective volume of the chamber. By effective volume, we mean the volume of the empty chamber from which we remove the volume of the devices.
Before concluding this section, we must point out that some chambers use the technology of copper welded walls. This method enables us to significantly reduce the thermal losses in the contact between the wall panels. The technology of the copper walls gives quality factors that are often higher than the steel walls. Users have however observed that a very high quality factor plays against the mode stirring efficiency. In order to reduce this high Q factor, some absorbing pieces, such as those coating the walls of anechoic chamber, may be inserted in the reverberation room. Therefore, a trade-off is found between the mode stirring efficiency and the ability of the room to produce high field strength amplitude.
4.2.3. Factors influencing the quality factor of a chamber
The definition of the quality factor of a cavity expressed in [2.66] but restricted to only one selected mode can be extended to an oversized cavity where an ideal random field distribution exists. In this case the electric energy WE and the power losses Pd appearing in equation [2.66] behave like random variables and must be replaced by their moment, i.e.:
[4.4]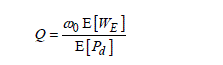 
However, the calculation of the moment of the variable WE can be avoided by forming the product of the electric energy density DWE with the volume of the chamber:
[4.5] 
The electric energy density comes from integral [2.65], from which we easily take the expression below:
[4.6] 
The Ew variable then represents the mean rms amplitude of the plane waves whose interferences form the ideal random field distribution. Readers interested in knowing more about the demonstration leading to the construction of the interferences of the plane waves can refer to section 3.3 of Chapter 3.
Knowing that a plane wave with an amplitude Ew carries a power density Dp rigorously similar to the product of Ew and the magnetic component Hw, the use of the plane wave impedance Zw and relationship [4.6] establishes the sought after link, i.e.:
[4.7]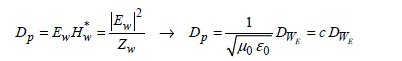 
The power density carried by the plane wave is thus the product of the celerity by the electric energy density stored in the chamber. This formula thus establishes the link between the interference of the plane waves and the theory of the cavities.
The average power losses in the denominator of equation [4.4] will result from the calculation of the moment found into equation [4.8].
[4.8] 
Indeed, this equation may by expressed in terms of the sum of several physical contributions successively involving: the power losses in the walls of the chamber Pd1, the power losses in the receiving antenna Pd2 and the power losses in the device under test Pd3.
This expression suggests allocating to the chamber, a composite Qg quality factor connected to the Q1, Q2 and Q3 coefficients associated with the three previous kinds of losses mentioned. We reach formula [4.9] [HIL 94a]:
[4.9] 
It thus remains to establish the analytical expression of these quality factors. Their contributions will be dependent on the ω0 angular frequency of the source, which is applied on a transmitting antenna.
4.2.3.1. The Q1 quality factor associated with the losses in the walls
Under the previous writing conventions, Q1 takes the expression:
We will adopt the formula of the mean quality factor stated in relationship [2.71] of section 2.3.6. This expression comes from the calculation of the mean value, whose computation method is exposed in Appendix 2:
[4.11] 
There are in this relation the volume V and the surface S of the cavity walls, as well as the electric conductivity σ and the relative magnetic permeability μr of the walls. Let us note that a better approximation of Q1 can be brought by formula [4.12], where there is an additional term containing a, b and d dimensions:
[4.12] 
It is not uncommon that the predictions established by relations [4.11] and [4.12] yield values five or ten times higher than the measured quality factors. The reason for these discordances is mainly imputed to the losses in the gaskets of the wall assembly, whose contribution is obviously omitted in these formulas. The use of an equivalent electric conductivity gathering the losses in walls and gaskets can solve the problem from the theoretical point of view.
4.2.3.2. The Q2 quality factor attached to the receiving antenna
The demonstration made in section 3.5.2 reached the expression of the average power collected by a receiving antenna, which is subjected to an ideal random field distribution. The formula is given below:
Let us recall that this formula is aimed at a matched antenna, with an antenna efficiency of η=1. If we enter the power density established in the room as presented in equation [4.7] and we determine the moment of equation [4.8], such an idealized antenna involves that the power collected by the antenna and the power at the output of the receiver are rigorously similar.
After coming back to the quality factor defined in [4.4] and to relationship [4.5] expressing E[WE], we reach the analytical form of Q2, i.e.:
Knowing that the ω0 excitation angular frequency and the λ0 wavelength are linked to the celerity c by [4.16]:
[4.16]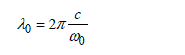 
The quality factor Q2 attached to the receiving antenna, perfectly matched and without losses, will be expressed according to relationship [4.17]. It appears as a function of only two parameters, the volume V of the chamber and the wavelength λ0:
[4.17] 
In the case of a mismatched antenna, the quality factor will be divided by the m mismatch factor.
If the antenna efficiency η is lower than one, this parameter should not be inserted into the calculation, since the thermal losses in the antenna are normally included in E[Pd2].
We can thus carry out the correction of the matching shown below:
4.2.3.3. The Q3 quality factor attached with the devices under test
Taking into account the various types of devices tested in a reverberation chamber, we cannot follow a unique path for the computation of Q3. However, the practice encourages us to distinguish two classes of physical phenomena, depending on whether the device is completely devoid of electromagnetic shield or if it is at least partially protected by a metal enclosure.
Without a highly shielded enclosure, the thermal losses given by the Pd3 variable found in equation [4.8] mainly include the contribution of the currents induced on any metal pieces of the device and more especially on the printed circuits boards (PCBs), which are major components of the usual electronic equipment. To shortly illustrate the induction phenomena on a PCB, let us consider only one trace of the circuit. This is similar with a transmission line formed by a single wire parallel to a ground plane of infinite size. Figure 4.1 shows the PCB trace with suitable geometrical parameters.
Figure 4.1. Illustration of the I(z) current induced on a PCB trace
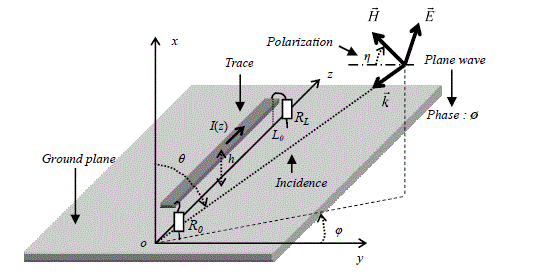
Let a plane wave with any incidence angle Ω impinge on the PCB trace. Its features are given in the spherical coordinate system by the θ and φ variables and by a polarization angle η and a phase angle α. Such a plane wave has the effect of inducing the current I(z) on the trace, as a function of the longitudinal variable z. If we assume the trace is located above the ground plane at a distance h much lower than the wavelength, the calculation of I(z) can be made using the transmission line theory. The power losses Ptk in the line will thus be the sum of the losses in the load resistances R0 and RL and of the thermal losses Pth in the high conductivity material of the trace and the ground plane respectively, i.e.:
If we are able to neglect the term Pth with respect to the power losses in the loads, the determination of overall losses only requires the calculation of the moments of the square of I(0) and I(L0) currents in the loads. Coming back to section 3.3.2 shows that the calculation can be practiced thanks to the simulation of an ideal random field by the trial of N plane waves all having the same Ew amplitude. The Ω, η and α variables are generated by Monte Carlo trials and the estimate of the < Pd3 > power losses takes the compact expression:
In this context, the size N of the sample of plane waves is determined by the uncertainty threshold expected in the statistical tests. At this point, the use of the law of the large numbers formulated in section 3.3.3 can be successfully experimented.
The estimate of the electric energy stored in the chamber is carried out by the direct transposition of relationships [4.5] and [4.6], i.e.:
[4.21] 
In equation [4.21], Ew represents the complex variable attached to the waves of the set N.
The Q3 coefficient will thus come from the estimate, which is determined by equation [4.22]:
[4.22]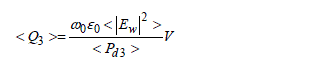 
When the device is protected by a highly shielded enclosure, the resulting power reaching the circuits inside the shield enclosure is similar, and even in some cases much lower than the thermal losses spread over the external surface of the shield which is directly exposed to the electromagnetic field. The determination of Q3 then comes within specific calculations or measurements.
Recent studies show that this calculation can be carried out without using random trials, but by means of an analytical formulation taking into account the natural correlation properties of the field [JUN 10].
4.2.3.4. Behavior of the composite quality factor versus the excitation frequency
The behavior of the composite quality factor of the chamber versus the frequency will play an important role in the ability of the chamber to produce large amplitude fields. In a lesser extent, the parameter intervenes in the efficiency of the mode stirring and during the emission measurements within the room.
To simplify the analysis, only the contributions of the Q1 coefficient relative to the walls and those of Q2, which is attached to the receiving antenna, will be considered. Relationships [4.11] and [4.17] established above will be transformed by making the excitation angular frequency ω0 directly appear, i.e.:
[4.23] 
[4.24] 
Using equation [4.9], the composite quality factor Qg of the chamber without devices will thus be written:
[4.25] 
Before introducing expressions [4.23] and [4.24] in [4.25], we simplify the writing thanks to the A1 and A2 coefficients defined below:
The composite quality factor of the chamber without devices other than the receiving antenna thus appropriates the general expression [4.28], which is dependent on the angular frequency variable ω0 of the signal supplied by the RF generator connected to the transmitting antenna.
[4.28] 
In practice, the layout of expression [4.28] shown in a graph drawn in logarithmic scales follows the behavior illustrated in Figure 4.2.
There is on the graph, the lowest usable angular frequency of the chamber designated by ωs, as well as the angular frequency ωt marking the area from which the thermal losses in the walls become predominant in comparison with the losses in the ideal matched receiving antenna. This specific angular frequency depends on the A1 and A2 coefficients, which are themselves dependent on the physical parameters stated above. For instance, rather than a conducting wire, an optical fiber that connects a field probe to a receiver, tends to reduce the losses, thus lowering ωt.
We observe the opposite behavior after the insertion in the chamber of pieces of absorbing materials:
Figure 4.2. Typical behavior of the quality factor in a reverberation chamber versus the angular frequency
As an example, let us consider a chamber of dimensions 1.9 m x 2.5 m x 2.8 m, whose fs is around 500 MHz. We know that the walls are made up of a steel with an electric conductivity close to 106 S/m and a relative magnetic permeability considered to be close to one within this frequency range. With the help of relationships [4.24] and [4.25], we find the numerical values of Q1 and Q2, which are calculated at 500 MHz and 2 GHz:
[4.30] 
[4.31] 
These values prove that close to the lowest frequency of 500 MHz, the composite quality factor mainly comes from the losses in the receiving antenna. On the contrary, for frequencies above 2 GHz, it is shown that the composite quality factor Qg is mainly due to losses in the walls. For these physical parameters, the specific frequency ωt is close to 700 MHz.
4.2.3.5. Role given to the transmitting antenna
Let us come back for a little while to Figure 3.5 in Chapter 3. It shows the power balance carried out for a transmitting antenna. According to this diagram established for the antenna transmitting in free space, the radiated power is Ptr. When this antenna is installed in a reverberation cavity, the electromagnetic interaction with the field reflected on the walls of the cavity causes a coupling. The latter manifests itself by a power entering the antenna. This phenomenon modifies the reflection coefficient defined in the BB’ plane. In others words, this means that the power effectively injected into the chamber is no longer Ptr, but a power Ptr’ lower than the previous one. The ability of the chamber to produce a field is thus reduced. Intuitive reasoning indicates that this coupling reaches the maximum, when the f0 excitation frequency is tuned on an eigenmode of the cavity. Consequently, any attempt to predict the field amplitude in the chamber must be done from the contribution of Ptr’. Generally, the reflection coefficient due to the transmitting antenna can be evaluated with the help of a network analyzer or a directional coupler. In that case, the power balance in the chamber is carried out on the only evaluation of Ptr’. This straightaway rules out the participation of the quality factor of the transmitting antenna. Indeed, for a chamber made up with perfectly conducting walls, the Ptr’ power vanishes if we assumed the antenna ideally matched and its efficiency to be one.
Without direct measurement of the reflection coefficient of the transmitting antenna, alone the injected power Pi enables us to determine the amplitude of the field in the room. In this case, it is imperative to determine the quality factor of the transmitting antenna. About this point, the analogy with the 1D model will facilitate the understanding.
Indeed, the behavior of a mismatched transmitting antenna is similar to the current generator, which is connected on the 1D cavity in Figure 2.3. Without any inner admittance, the generator does not provide thermal power. It thus results that the tuning on the eigenmodes causes a resonance characterized by an infinite amplitude voltage. The inner conductance of the generator thus has the effect of damping the cavity and of bounding the amplitude of the voltage to a high value, but not infinite. Under these conditions, the analogy of the cavity with a RLC resonator, enables us to merge the behavior of the cavity with the frequency response of a resonant circuit. The details found in section 2.2.4 remind us about some elements of the circuit theory, which is applied to this case.
Let us transpose the previous reasoning for a 3D cavity, which is made up of perfectly conducting walls and is empty of any device, except for the transmitting antenna. During resonance, the only phenomenon able to damp the cavity will be the losses of the power by back scattering of the waves in the transmitting antenna. Then, if we install, in this ideal cavity, a non-lossy field probe and if we measure with a network analyzer the S21 scattering parameter between the antenna and the probe, exploration of the frequencies close to the expected resonance of the cavity will set a maximum amplitude; this finite amplitude is directly due to the incoming reflected waves into the transmitting antenna. The response measured close to the tuning frequency of a selected mode, will thus be similar to the behavior of a resonant circuit.
The measurement processes of the quality factor of a reverberation chamber will be detailed further in section 4.3.
4.2.4. Space correlation of an ideal random electromagnetic field distribution
A reverberation chamber configured for producing ideally random standing waves must thus meet the criteria of the stochastic processes which are recommended in the previous chapter. The chamber cannot be perfectly oversized with respect to the wavelength. Therefore, we must expect that the field samples that are very close together in the space take partially correlated amplitudes. In other words, in order to collect statistically independent data, samples must be collected at a distance from each other higher than a minimum distance defined from the correlation feature of the field distribution. A development directly borrowed from the works published by D.A. Hill enables us to easily link this parameter to the wavelength [HIL 95, HIL 02].
Let us consider two observers located at the P1 and P2 points, themselves at distances r1 and r2 from the origin of the oxyz coordinate system in Figure 4.3. Let us designate by 
and 
, the complex electric field vectors at the points P1 and P2. Since it is more convenient to configure the calculation in a spherical oθφr coordinate system and in order to simplify the notations, the use of the 
and 
vectors has been preferred over the three θ, φ and r variables.
The computation is based on the assumption that the ideal random field comes from the interference of N plane waves, with random trials under the conditions specified in section 3.3.2. First of all, the analytical formulation of the problem rely on the definition of the correlation coefficient, which is given on the basis of the geometrical graph in Figure 4.3.
According to the elements stated in Appendix 1, the correlation coefficient is calculated by the ratio given in formula [4.32]. There is at the numerator the expected value of the scalar product of the field vectors. At the denominator the square root of the product of the moments of each square amplitude of the vectors is found. The star on 
corresponds to the complex conjugate value:
[4.32] 
Figure 4.3. Coordinate system for the calculation of the correlation coefficient
Taking a look at equation [3.128], established in section 3.5.2, shows that the moments are merging with the square amplitude allocated to the plane waves, i.e.:
The calculation of the numerator of [4.32] will be carried out with the use of the spectral function 
which is defined by equation [3.125]. The following part of the calculation reaches the sequence of two integrals:
[4.34] 
We will not reproduce here the full development; readers will find further details in the references.
Equation [4.34] comes down to only one integral which is formulated as follows:
After calling on the variables of the spherical coordinate system, this integral becomes:
This equation may be solved immediately and leads to the analytical form of the correlation coefficient, which is represented by a sine cardinal function including the product of the k wave number and of the absolute value of the difference of the 
and 
position vectors:
[4.37] 
The demonstration proves that in the resulting field of ideal random plane wave interferences, the collected random variables are not necessarily independent. When the norm of the term 
is called Δr, equation [4.37] takes the simplified form [4.38]:
[4.38]
The position of the first zero of this function determines the extension of the main pattern of the cardinal sine and consecutively the criterion that we propose to use in order to determine the Δrc correlation distance, i.e.:
[4.39] 
Knowing that the k wave number is given by the ratio of 2π over the wavelength, from [4.39] we easily find that the correlation distance takes the remarkable value λ/2:
We will see in the next section that the correlation distance plays a major influence when acquiring a data sample through a stirring method. However before tackling this matter, we need to point out that the correlation does not only concern the field amplitude, but also the polarization. Close to the walls of the chamber or to any other metal device, the tangential component of the electric field is almost zero, as well as the normal component of the magnetic field. This is the case for the electric field vector 
illustrated in Figure 4.4. The ox and oy axes of the oxyz coordinate system are merged on the highly conducting plane of the wall. The use of unit vectors attached to this graph enable us to express the complex vector under the form of a function of the three x, y and z variables.
On the surface of the wall, the electric field vector thus takes the amplitude:
Because of the boundary condition involved by the very high electric conductivity of the metal walls, the tangential projections of the electric field close to the wall vanish and consequently move away from the expected behavior of the random variables. In this area, the tangential components will thus be subjected to an amplitude correlation, whose space extension will depend on the wavelength. If the excitation frequency of the field is tuned on an eigenmode or close to a group of modes, the maximum amplitude of the standing waves thus constituted will take place at a distance from the wall of about λ0/4, where λ0 is necessarily given by the frequency emission f0 in the chamber. We can thus conclude in accordance with the description in Figure 4.4, that in the space going from z = 0 to z = λ0/4, the behavior of the Ex(x,y,z) or (and) Ey(x,y,z) functions will be determined by almost a sine wave function.
However, for distances overlapping λ0/4, these functions behave in a random fashion as we move away from the wall. In other words, this property means that a reverberation chamber only gives ideal random fields distribution if we do the measurements inside a dummy rectangular shaped volume latter so called working volume, whose outlines are at least a distance of λ0/4 from the highly conducting walls of the room. For a chamber with 1.9 m x 2.5 m x 2.8 m dimensions with a lowest usable frequency of 500 MHz, i.e. a wavelength of 60 cm, this working volume will be made up of a parallelepiped with 1.6 m x 2.2 m x 2.5 m dimensions.
Figure 4.4. Context of the electric field projection close to a wall
4.3. The usual techniques of mode stirring
4.3.1. Mechanical mode stirring
The physical properties of the mechanical mode stirring introduced in section 2.4 of Chapter 2, showed that the rotation of a stirrer with metal paddles mainly influences two parameters of the chamber. Indeed, during the rotation of the stirrer, the modal frequencies are shifted and their extent will depend on the dimensions and on the geometry of the size of the paddles. A field dislocation is added to this first phenomenon, which is particularly significant as the stirred field volume gets close to or largely overlaps the volume of the modal cells. The concept of modal cells is briefly described in section 2.3.4 of Chapter 2.
Section 3.3.1, calling on the analysis in the wave number domain, introduced the construction of the plane waves model. The effect of the mode stirrer is therefore seen as similar to the production of the interferences of a large number of plane waves, whose incidence, polarization and phase angles are randomly distributed. To get close to the analogy of the field in the chamber with this model, it seems obvious to break off, in the strongest possible way, the symmetry of the rectangular room. The mode stirrer can thus contribute to establishing these features.
To tell the truth, there are no specific recommendations for the construction of mode stirrers and there exists many types of them with various geometrical shapes and dimensions. Nevertheless, we can find some criteria which are deduced from experience and research of the phenomena mentioned above.
The stirrer will be preferably installed away from the symmetry axes of the rectangular room. Figure 4.5 shows the off-center location of a mode stirrer, whose rotation axis is vertically positioned between the ground floor and the top wall of the chamber. In order to further increase the asymmetry, the a0 and b0 coordinates of the rotation axis of the mode stirrer will be chosen in an irrational ratio of the a and b dimensions of the walls. The paddles shape will be as different as possible, in order to also increase the asymmetry during the rotation. However, the preservation of the mechanical equilibrium will require blades of a similar mass.
Figure 4.5. Typical asymmetric arrangement of a mode stirrer
To reconcile this condition with the sought after asymmetry, the blades will be constituted of two-sided conducting planes so called dihedrals. The choice of their fold angles will impact the electromagnetic coupling and consecutively the effect of the stirrer. Figure 4.6 shows such a realization. The θ1 and θ2 fold angles can be adjusted during the installation of the stirrer, in order to produce the expected asymmetry.
The mode stirrer is moved with the help of a motor with variable speed, which is generally positioned above the top wall of the chamber. The motor can be operated to produce continuous or stepped angular deviations so called latter mode stirring and mode tuning procedures. The stirrer positioning system requires the establishment of a reliable and accurate angular detector. The use of the mode stirring or mode tuning procedures will depend on the focused application.
Figure 4.6. Blades made up of dihedrals with adjustable θ1 and θ2 fold angles
4.3.1.1. The mode stirring procedure
Under the mode stirring procedure, the stirrer is moved by a uniform rotation speed. The collection of data is carried out at periodic time intervals. The period is fixed by the characteristics of the tested equipment and of the receiver performances. For example, voltage measurements of very low amplitude are carried out with a spectrum analyzer which is tuned on a very short resolution bandwidth of few tens of Hz. These measurements will thus require very slow rotation speed of the stirrer, which is imposed by the long time response of the narrow band filter of the receiver. In other cases, the stirring procedure reduces the consuming time of the measurements. Nevertheless, we have to admit that the mode stirring procedure does not enable us to reach rigorously the steady state of energy stored in the room. This drawback plays against the testing reproducibility.
4.3.1.2. The mode tuning procedure
In the mode tuning procedure the rotation of the stirrer is stopped at periodic angular positions. On each dwell position, the resulting data of the test are collected. The mode tuning procedure is especially devoted to the immunity tests and the emission measurements involving either a narrow or a large frequency range. The duration of the dwell time is fixed by, the steady state of the energy in the room and the time required detecting a fault of the electronic equipments submitted to the immunity test.
4.3.1.3. Measurement of the efficiency of a mode stirrer
The processes used in order to test the efficiency of a mode stirrer will mainly be discussed during the next section, which is devoted to the characterization of the chambers. Alongside the standard procedures, the method of the mean statistical distance is generally a sufficient criterion to evaluate the behavior of the mode stirrer, as a function of the frequency. This method requires the use of a transmitting antenna with a large frequency band. On a rotation of the mode stirrer, we collect N data of power on the receiver connected to the antenna. During the test, the power injected on the transmitting antenna can be maintained as invariant. This condition is not however essential. For each explored frequency and for each sample of N data, we determine the absolute value of the distance Δi associated to the difference between the theoretical cdf F2(xi) and the experimental histogram SN(xi), i.e.:
[4.43] 
Let us recall that the construction of the theoretical cdf is described in section 3.4.2. The test consists of estimating the arithmetic mean Δ, which is then compared to a reference value:
[4.44]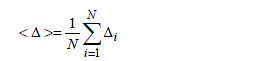 
Looking at possible arrangements of a mode stirrer, this method, which is more simple than the KS test, provides some interesting data to assess expected improvements. Furthermore, the determination of the mean distance Δ is an easier way to evaluate the lowest usable frequency of the chamber.
4.3.1.4. Mixed mode stirring
Mixed mode stirring consists of increasing the size of the samples of the stochastic data in moving a second mode stirrer. Indeed, we will see during the process of characterization of the chambers that a mode stirrer can be designed by an angular correlation coefficient, whose estimation leads to the number of independent data which are collected during a rotation. Knowing that this criterion is dramatically reduced as soon as we get close to the lowest usable frequency of the chamber, we sometimes have to practice a combined stirring, in accordance with the description below.
The angular positions of the main mode stirrer are determined by the collection of independent consecutive data. It is assumed that between two of them, the physical properties of the chamber have been sufficiently altered, in order to redistribute the field in a purely random fashion. Under this condition, the installation of a second mode stirrer brings an additional degree of freedom which allows the insertion of other independent data forming a new stochastic sample of size N’.
According to this fact, the N data collected by the main mode stirrer will be mixed with the N’ data collected during the rotation of a second stirrer. The size of the statistical sample thus goes to NN’.
We will find again, during the field calibration procedure described in section 5.2 of Chapter 5, that the practice of mixed mode stirring is a way to improve the efficiency of the reverberation chamber in order to reduce the natural uncertainty of the field amplitude distribution.
Let us point out that mechanical stirring can be combined with the frequency agitation or stirring by switching or random displacement of the transmitting antennas described in the following sections.
4.3.2. Frequency agitation of the modes or electronic stirring
In a narrow Δfa band located on a fa central frequency, experience shows that mechanical mode stirring is not uniformly efficient. The data gathered in Table 4.1 comes from a test, where mechanical mode stirring and frequency agitation are mixed.
Table 4.1. Positions of the <Δ>average distance within a short frequency range
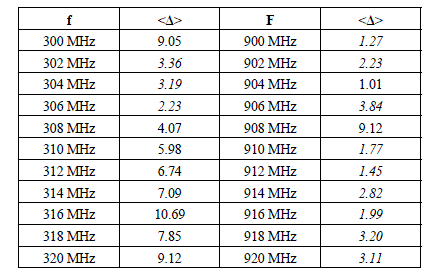
The chamber used during these experiments has the lowest usable frequency, fs = 500 MHz. The measurements have been performed at 11 frequencies uniformly distributed on two ranges Δfa of 20 MHz, themselves located on two central frequencies fa at 310 MHz and 910 MHz, located on both sides of fs. This choice will enable us to produce the standing waves in two different frequency ranges where the efficiency of the mode stirring is deeply impacted. In Table 4.1, facing each frequency there is the <Δ> mean statistical distance expressed in % and relating to the definitions coming from expressions [4.43] and [4.44] of the previous section. A confrontation to the KS test has shown that a mean distance <Δ> of about 3% or below this threshold corresponds to the conditions required by a field approaching the ideal random field distribution.
Consequently, the numbers in italics select for each batch the frequencies where we observe an efficient mechanical mode stirring. As expected, for the emission at 310 MHz located below fs, we collect only 27% of the batch of the 11 frequencies in accordance with the criterion of efficient stirring. Conversely, we find that the emission produced at 910 MHz takes the success rate up to 82%. Let us note that, although located one octave above fs, the frequency agitation carried out around 910 MHz does not fully give an efficient stirring. We can thus conclude that without a mode stirrer, an excursion of the Δfa frequency more or less extended around a central fa frequency is an alternative way to mechanical mode stirring. The physical reason of this behavior is based on the random renewing of the field distribution, which is correlated to the energy distribution of the modes randomly excited in the narrow frequency response around fa. Thanks to relationship [2.100] introduced in section 2.3.9, we know that the Δfm n p bandwidth is associated with any mode tuned on the fm n p frequency, taking the expression:
[4.45] 
The quality factor Q1 in the denominator of this expression is related to the thermal losses in the walls of the room such as is recounted in formulas [4.11] and [4.12].
If we assume the emission frequency f0 is sufficiently high to reach the oversized behavior of the chamber and if we take into account the coupling with the antennas and the presence of the device under test, relationship [4.45] becomes:
In this new expression, Δfg represents the bandwidth related by Qg the composite quality factor of the chamber.
In section 4.2.4, we have shown that the random field distribution in the room is characterized by a Δrc correlation distance, which leads to the specific value λ0/2. Translated in the frequency domain, the space correlation is similar to a minimum frequency distance Δfmini giving the collection of statistically independent data. With regards to frequency agitation, this feature means that two neighboring frequencies within the Δfa range must at least be distant from Δfmini.
The criterion enabling us to specify the minimum frequency distance can be found by comparing Δfmini to the Δfg bandwidth, which is occupied by the modes located close to the f0 emission frequency. To assess these parameters, let us consider the numerical example discussed in equations [4.30] and [4.31]. We calculated for the reference chamber operated at the frequencies of 500 MHz and 2 GHz, two values of the composite quality factor located at 9,000 and 50,000. We can thus deduce from the previous development that the frequency correlations merged with Δfg will be 55 kHz and 40 kHz:
Knowing that the experimental data shown in Table 4.1 is aimed at a chamber with characteristics similar to the current example, the increment of 2 MHz is thus largely justified in order to come away from the correlation distance.
4.3.2.1. Stirring by frequency hopping
The tests by frequency hopping mainly concern the immunity tests carried out in accordance with the frequency agitation procedure and independently from the rotation of a mode stirrer. We carry out the selection of N central frequencies fa; each of them attached to a Δfa range including N’ emission frequencies. For the reasons mentioned above, Δfa must be much lower than fa. In the presence of a device under test with a narrow Δfr frequency response around a resonance frequency fr, the excursion range Δfa of the emission frequencies will thus be below Δfr. Without this precaution, the measurement would be affected by bias errors.
4.3.2.2. Continuous frequency agitation
In order to reduce the execution time of some tests, it can be interesting to practice the continuous frequency agitation. This well known method consists of mixing the emission of the f0 frequency with a broadband noise signal. The block diagram in Figure 4.7 illustrates the signal generation used for this procedure [HIL 94b, LAM 96].
Figure 4.7. Block diagram of a RF generator configured for the continuous frequency agitation
If the noise is characterized by the random function b(t), the signal processing theory shows that the spectrum of b(t) may be characterized by Sbb( f ) which is the Fourier transform of the correlation function cbb(τ) of b(t). Then, we can show that the spectrum Sss( f ) of the random function s(t) at the output of the mixer circuit will be expressed in accordance with expression [4.49]:
[4.49] 
If we assume a noise spectrum with a uniform amplitude bounded by the Fb frequency, the latter will necessarily be lower than f0. Figure 4.8 brings the graphical transposition of relationship [4.49] restricted here to the only positive frequencies.
The excursion of the Δfa frequency band will thus be determined by 2Fb. This process involving a fast frequency agitation, the immunity test of electronic equipment which generally requires long response times, seems to be unsuitable.
Nevertheless, this method can be applied to the measurements of the effectiveness of the shield, with the condition that the response of the devices lies within a not excessively too small frequency range such as resonances found in shielded enclosures. The continuous frequency agitation is particularly well suited for the devices with a uniform frequency response.
Figure 4.8. Spectral figures of the noise and of the signal configured for the use of continuous frequency agitation
4.3.2.3. Combination of frequency agitation with the mechanical stirring
As proven by the results shown in Table 4.1, stirring by frequency hopping can easily be combined with mechanical mode stirring, in order to increase the size of the statistical samples.
4.3.3. Stirring by switching the transmitting antennas
Mode stirring by antenna switching requires the installation of N transmitting antennas in the reverberation chamber. Generally, these antennas have similar characteristics, especially in terms of field pattern, but they are polarized and located with a random fashion in the room. To carry out the immunity tests, the antennas will be successively switched to a RF generator located outside the chamber [MON 08].
Compared to mechanical stirring and to frequency agitation, the only degree of freedom of the switching antennas method will be determined by the excitation level of the modes. Indeed, coming back to the 1D model presented in section 2.3.7, shows that a random displacement of the dipole inside the Fabry-Perot cavity modifies the coupling on whether the dipole will be located close to zero or close to a peak magnitude of the standing wave. We know that in an empty cavity, the wave displays rigorously a periodical pattern, which means that even a random distribution of the antennas will produce a field governed by a non random distribution.
Conversely, if the cavity obeys the oversized behavior, the losses produce modal interferences, whose mechanisms will be increased by wave scattering from devices located in the room. Switching the transmitting antennas thus has the effect of renewing the wave in an almost random way. The process is then similar to a mode stirring, whose efficiency is more significant using many randomly positioned antennas.
In a way similar to the switching of the transmitting antennas, we can carry out the displacement of only one antenna in several random locations of the chamber. This method requires a longer execution duration than the previous one. However, it offers simpler implementation. Moreover during the displacement, the coaxial cable linking the antenna to the RF generator located outside the chamber behaves like a scattering device improving the efficiency of the stirring.
We generally combine the stirring by switches or by displacement of the transmitting antenna with the mechanical stirring, in order to increase the size of the statistical samples. The process is then similar to a mixed mode stirring.
4.3.4. Mode stirring by dimensional modulation of the chamber
Mode stirring by dimensional modulation of the chamber consists of producing an excursion of the eigenmodes, by carrying out a short displacement of the metal walls of the chamber [LEF 00]. The process finds its physical explanation in expression [4.1] recalled below:
[4.50] 
This formula calculates the m, n, p natural mode of an empty rectangular cavity.
The process subjects the a, b and d dimensions of the chamber to displacements Δa, Δb and Δd, whose amplitude range remains much lower than the original dimensions:
[4.51] 
While respecting these conditions, the resonant frequency of the fm n p chamber will be modified in order to take the f’m n p value shown below:
In the case of the small variations recounted in [4.51], the use of the first term in the series expansion of equation [4.50], leads to the following approximation of Δfm n p, i.e.:
Examination of this equation shows that by giving random amplitude variations to the Δa, Δb and Δd parameters, the resonant frequency of the chamber will also undergo random fluctuations around the emission frequency f0, resulting in a random behavior of the field amplitude. The process is thus quite similar to mode stirring.
The practical implementation of mode stirring by dimensional modulation has been successfully carried out by F. Leferink, by means of a rectangular chamber of walls made up of metal textiles distorted by six actuators, in accordance with the diagram in Figure 4.9.
Figure 4.9. Illustration of the actuators producing a dimensional modulation of the room
The locations of the actuators are marked by numerical data, which are monitored by software. This function is similar to the angular positioning of a mechanical mode stirrer.
Stirring by dimensional modulation can be freely applied to the immunity tests as well as to the emission and shielding effectiveness measurements.
To increase the size of the samples of the statistical data, it can be combined with the frequency agitation.
4.4. The characterization of reverberation chambers
4.4.1. Aims of the characterization of reverberation chambers
The characterization of the chamber aims at a purpose other than the calibration process tackled in Chapter 5. The characterization proposes theoretical tools or experiments enabling us to evaluate the compliance of the chamber with the expected physical features. The calibration concerns the measurement procedures recommended by international standards to check the ability of a chamber for carrying out measurements or reproducible tests [LAD 99].
Among the parameters studied in the characterization, we will find successively, the determination of the efficiency of the mode stirring, the research of criteria showing the stochastic stationary nature of the field, the measurement of the quality factor and the location of the lowest usable frequency of the chamber.
The characterization of the efficiency of the mode stirring and the determination of the lowest usable frequency fs are somewhat linked. Indeed, the random distribution of the field in the room which is generated by mode stirring closely depends on the position of the frequency emission f0 with regard to fs. The analysis will be restricted to the mechanical mode stirring that remains the most used in the testing centers.
The stochastic stationary criterion of the random field distribution is expressed in terms of standard deviation compared to the mean amplitude or to the maximum amplitude of the field data, which are collected during a rotation of the mode stirrer. As previously mentioned and for the same reasons, we will limit ourselves to mechanical stirring.
We know that the value of the composite quality factor of a chamber expresses the ability of the cavity to produce a high electromagnetic field amplitude under a low RF emission power. Furthermore the value of the quality factor provides the modal bandwidth, whose contribution is to be related to the efficiency of the mode stirring by frequency agitation. On the other hand, it was shown that the quality factor is also involved during the emission tests. Considering the major role played by this parameter, section 4.4.3 will be entirely devoted its measurement methods.
4.4.2. Characterization of the efficiency of mode stirring
4.4.2.1. Measurement of the modal dislocation
This test consists of assessing the ability of the mode stirrer to produce the conditions of an ideal random electromagnetic field as described in the previous chapter. Indeed, the rotation of the mode stirrer amounts to reconfiguring the geometrical properties of the chamber. There results from it a modal dislocation leading to the establishment of a distribution field of random amplitude. Generally, this test requires measurements, whose procedure is explained below. We need to point out that numerical computations performed with the contribution of full wave software offers alternative way to determine improvement in the shape and geometrical parameters of the mode stirrers [ELH 09, FIA 09, LAL 06].
The experiment requires a transmitting antenna, which is connected to a RF generator of frequency f0, which is above the lowest usable fs of the chamber.
We assume fs to be unknown but located about five or six times above the first eigenmode of the chamber. Moreover, in order to increase the probability of success of the test, we will use a transmission frequency f0 two or four times higher than fs.
When the random data collected in the experiment come from a receiving antenna, it will be the power measured on the receiver. If the measurements are performed with an electric field probe, these data consist of the voltage measured on the probe.
Reducing the direct electromagnetic coupling between the transmitting antenna and the receiving antenna (or the probe) as much as possible, we collect and record N data of power or of voltage during a rotation of the mode stirrer. They will be uniformly distributed on the full angular coverage of 360°. In the context of this experiment, the number of data does not really matter. We will select at least a sample size of N=100 in order to have a sufficient set of data for the construction of the cdf histogram.
The measurement of the modal dislocation must give the proof that the rotation of the mode stirrer distributes these data with the biggest random fashion. The theoretical cdf used as reference will be related to the condition involved by the ideal random field distribution and the type of data. If it is the power on the receiving antenna, the cdf comes from the integral of the pdf given by the exponential distribution. For the voltage collected on a field probe, we use the Rayleigh distribution. Depending on whether we measure the power or the field, the layout of the theoretical cdf will require the estimate of the mean amplitude or of the variance of the recorded data.
Once these cdf curves are thus displayed the next step will consist of using the Kolmogorov—Smirnov test, which is described in section 3.4.4 of Chapter 3.
Generally, we set the significance level or risk threshold of the test at 5%. If the test is accepted, we repeat it by carrying out frequency hopping around f0 by getting close to the criteria mentioned in section 4.3.2. If the test is rejected and to check that this behavior is indeed stationary, we repeat the measurements at emission frequencies sufficiently far away from f0. As a function of the requirement of the measurement, we can get close to the agreement theory/experiment by enlarging the risk threshold to 10%.
4.4.2.2. Measurement of the stirring ratio
The stirring ratio is related to the amplitude excursion of the power and voltage collected on antenna or probe as a function of the angular position of the mode stirrer.
The stirring ratio, designated by SR, characterizes the ratio of the maximum amplitude and of the minimum amplitude of the previous data collected during a rotation of 360°. Generally, SR is expressed on a scale in dB. Depending on whether the data comes from the p power or from the V voltage, we adopt the following formulae of SR:
A stirring ratio that is too low has the sign of a significant contribution of the direct electromagnetic coupling due to the RF emission generated in the room. Normally, it is admitted that efficient mode stirring gives a SR coefficient higher than or near to 20 dB. Let us specify that the measurement of the stirring ratio made on the field probes rarely exceeds 20 dB because of the non-linear behavior of these electronic devices.
In Table 4.2 the measurements of SR are gathered, which are recorded in a chamber whose fs is located at 500 MHz. Batches of 11 emission frequencies contained in a band of 20 MHz, which is centered on 310 MHz and 910 MHz, give the value of SR expressed in dB.
Table 4.2. Behavior of the stirring ratio on both sides of fs, which is located at 500 MHz
The data in italics correspond to SR values which are near to or higher than 20 dB, i.e. the conditions assumed to give an efficient mode stirring. For the frequency of 310 MHz located under the lowest usable frequency of the chamber, this test gives a 54% success rate. At 910 MHz, i.e. an octave above fs, this rate goes up to 90%. We will notice the strong correlation with the measurements of the mean deviation < Δ >, which are reproduced in Table 4.1.
4.4.2.3. Estimate of the correlation angle of the mode stirrer
In section 4.2.4, calculations based on the use of the plane wave spectra have shown that interferences of randomly distributed plane waves generate a correlation distance of half a wavelength. In other words, this means that a moving observer in the room will perceive a strong correlation of the field amplitude during small displacements compared to λ0/2. Consequently, two samples of data collected within an interval of λ0/10 are not statistically independent. If the random distribution of the field is assumed to be stationary, this property will be extended at any location in the chamber. The respect of the correlation distance of λ0/2 is thus essential condition for the collection of data in the view of the computation of mean values or of variances.
Intuitively, the field correlation detected for a moving observer can be extended to a motionless observer carrying out the measurement of the field in the chamber during the rotation of the mode stirrer. Thus, a sample made of consecutive data collected after an angular deviation θ that is too small could be excessively correlated to constitute a reliable statistical sample. There is thus a parameter Δθc, so-called correlation angle, of the stirrer above which the data get close to the criterion of statistical independence.
The determination of Δθc is carried out in evaluating the correlation function of the mode stirrer. We adapt to this particular problem the definition of the correlation coefficient, which is introduced by expression [4.32]. Knowing that we aim here at the measurement of the absolute electric field amplitude and of the power which is collected by a receiving antenna, we will use centered variables designated by the symbols xi and yi. If p represents the power on a receiving antenna, xi and yi are expressed as:
Under these specific notations, the function p(θi) corresponds to the power data measured at the angular position θi of the mode stirrer, whereas < p > forms the estimate of the mean amplitude of p. For NS stirrer positions uniformly distributed with a rotation angle Δθ, <p> takes the expression:
The determination of the correlation coefficient is thus given in the expression [4.57] where we find the estimate of the variances of the x and y data practiced according to the computation found in relationship [3.109] set out in section 3.4.3:
[4.57] 
The correlation data are generally displayed in a graphical layout close to the illustration of Figure 4.10.
There is on the horizontal axis the angular deviation of the mode stirrer. Knowing that the correlation has a period of 360°, only half of the data restored by the calculation will be kept. This reason explains the reduction of the k index to the [0 NS/2] interval. The latter is mentioned in expression [4.57]. The values of ρ carried by the vertical axis will be normalized to one for the null angular deviation, i.e. for k = 0.
There is a criterion recognized by the international standards for the determination of the correlation angle Δθc. This criterion is reached when ρ goes below the numerical value 0.37. The choice of this threshold number has probably been guided by the shape of the curve which is very close to an exponential decay. Let us recall that the correlation function of a random signal collected at the output of a first order low-pass filter, which is stimulated by a white noise leads to an exponential function.
Figure 4.10. Typical shape of the curve of the correlation coefficient of a mode stirrer
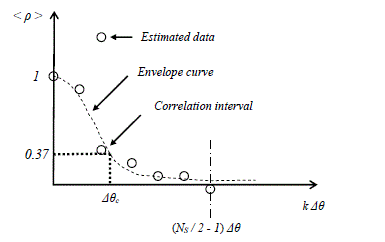
The correlation angle Δθc of the mode stirrer is lower as the chamber evolves towards an oversized behavior compared to the wavelength of the generated field. We will see in section 8.3 of Chapter 8 that recent research studies help us to more precisely refine the correlation and statistical independence criteria of the data collected during a rotation of the mode stirrer.
4.4.3. Test of the stationary random electromagnetic field distribution
The boundaries of the working volume are described in section 4.2.4 and located at a minimum distance from the walls of a quarter of the wavelength. In this volume, the condition of the stationary random field means that the data of the electric or the magnetic field collected in this space must meet the criterion of the largest random behavior.
In accordance with equation [3.28] formulated in section 3.2.5, the chosen criterion indicates that the random variables attached to the absolute amplitudes of the electric field must satisfy the Rayleigh distribution, for which the pdf is pR(er). We will recall here its expression for the normalized field variable er:
[4.58] 
In this formula found in section 3.2.1, the σv parameter represents the standard deviation attached to the real and imaginary components of the complex variable Ex,y,z.
The stationary random field is thus to be linked to the behavior of |Ex, y,z| within the working volume.
This section will be continued with the basic theory for the calibration of stationary random field as suggested by the international standards.
4.4.3.1. Estimator of the mean amplitude of the field
We assume that independent random data are collected on a field probe successively located Nc positions. The distance step between them is chosen to be larger than the correlation distance of λ0/2. This enables us to carry out an estimate of the mean amplitude. This estimation, under the < er > notation, results from the use of formula [3.105] introduced in section 3.4.3:
We can thus extend to this calculation of the mean what was discussed in section 3.3.2 about the uncertainty margin produced in the simulation of an ideal random field distribution. Indeed, according to the central limit theorem it was shown that the pdf attached to the normalized random variable zr follows the normal distribution. We recall that zr represents the deviation between the estimate of the mean < er > and the moment of er,
[4.60] 
We point out that the standard deviation of the estimated variable < er > appears in this relation. This parameter can easily be related to the standard deviation of er by means of equation [3.73] involving the law of large numbers, i.e. with the current notations:
[4.61] 
In experiments it is often more convenient to deal with the true physical variables rather than the normalized field variables. The problem then consists of converting pdf expression [4.60] by the insertion of the Eη variable. The latter this time links the deviation between the mean estimate and the moment of the absolute field amplitude, i.e.:
[4.62] 
By carrying out a few algebraic transformations involving the definition of the random variable er and its variance recalled in equations [4.58], and [3.72], the combination of [4.61] and [4.62] leads to a formula of zr containing only Eη, Nc and σν:
After insertion of this variable into equation [4.60], we obtain the pn(Eη) pdf, directly dependent on Eη, i.e.:
[4.64] 
This expression shows that by increasing the size Nc of the sample of random data, the standard deviation σE of the Eη variable is reduced and as a result there is a lower uncertainty of the estimate of the field mean amplitude. The layout of function [4.64] enables us to determine this parameter; this assumes however that the σv standard deviation attached to the complex electric field variable Ex,y,z is preliminary known.
4.4.3.2. Estimate of the σν standard deviation
Knowing that σν is involved in the definition of the normalized variable er recalled in equation [4.58], computation of the moment of this equation and insertion of the numerical data found in [3.69] leads to the value of σν.
[4.65] 
Since the mean field amplitude cannot only be known by estimate, we take 
from expression [4.65], i.e.:
[4.66] 
Let us point out that the estimation of σv is carried out by equation [4.66] and is affected by a bias error. This means that, strictly speaking, must be evaluated by making the correction formulated in section 3.4.3. This last procedure is however only possible when the field probes collect the complex amplitude of Ex,y,. However, in practice, the more usual field probes give only the absolute amplitude of Ex,y,z.
4.4.3.3. Measurement of the uncertainty attached to the mean field amplitude
The detailed description of the field calibration made in Chapter 5 foresees the use of the crossing of the data collections in accordance with the method described below.
A first step consists of carrying out the mean estimate on NB field data collected during a full rotation of the mode stirrer, with the probe located on the boundaries of the rectangular working volume. So that these data are independent (at least uncorrelated), the data collection will be carried out at angle steps at least higher than the correlation angle Δθc defined in Figure 4.10. The estimate of the mean amplitude is then repeated for the three x, y, z polarizations of the field probe, as well as on Nc locations of the probe, in order to record 3Nc estimates of the mean with the dedicated notation 
where the bottom k index is related to one of the 3Nc samples:
The amplitude calibration is carried out on the mean over the all set of the 3Nc primary means 
i.e. formulated with the current notations:
[4.68] 
The uncertainty of the average amplitude of the field will be deduced from the estimate of the standard deviations of the 
data. The result will be compared to a reference value found in the calibration standard. We can notice that the estimator of the standard deviation will comply with the correction of the variance estimate, which is given by equation [3.109] in section 3.4.3.
4.4.3.4. Nth order statistic
Immunity tests of electronic equipment in a reverberation chamber requires the knowledge of the maximum amplitude rather that the mean amplitude of the field distribution. Consequently the calibration procedure will focused on the estimation of the maximum values of the data recorded during a full rotation of the stirrer. This also requires the determination of the uncertainty of the maximum amplitude collected at various locations of the working volume boundaries. This maximum amplitude uncertainty is evaluated through the concept of the Nth order statistic according to the computation of the pdf detailed below [ORJ 07].
Let us consider a vector X of N independent random variables x all attached to the same probability distribution. Let us call pA (x) the pdf and FA(x) the cdf related to x. The index A corresponds to the type of probability distribution. In case this index is 2, it is aimed at the exponential distribution and the index R is aimed at Rayleigh’s distribution:
We can show that the pdf of the maximum and minimum amplitudes of the x variables, the X vector takes analytical expressions [4.70] and [4.71]. In these formulas a specific bracket notation is adopted to distinguish the pdf related to the maximum or minimum values found in the X vector.
[4.70] 
[4.71] 
Readers eager to know more about the detailed developments leading to these formulas should refer to the book by A. Papoulis [PAP 91].
In this context, the evaluation of the maximum amplitude of the variables of the X vector can be represented by the calculation of the moment, i.e.:
[4.72] 
The mean amplitude of the maximum provided by this equation will be related to an uncertainty that depends on the variance of xmaxi, i.e.:
[4.73] 
However, in the frame of reverberation chambers applications, an analytical solution for the integrals found in equations [4.72] and [4.73] is only available for the exponential pdf. This context straightaway implies the use of the power variable p.
4.4.3.5. Estimate of the maximum field amplitude
For a given location and polarization of the field probe which is installed at the boundaries of the working volume, the estimate of the maximum field amplitude consists of checking the maximum from among NS independent data. These data are released during a rotation of the mode stirrer. It is thus a question of knowing the uncertainty with which this maximum amplitude can be evaluated. The calculations of mean value and variance, which are expressed in equations [4.72] and [4.73], then manage to target this uncertainty.
We know that the absolute amplitude of an ideal random electric field distribution expressed in terms of absolute values |Ex,y,z| follows Rayleigh’s distribution. However, the insertion of the Rayleigh pdf into the previously detailed equations excludes the analytical solution of the integrals. Only the exponential distribution attached to the power is more attractive to solve these integrals. A calculation, whose development is not currently interesting, shows that the pdf attached to the minimum amplitude can restore an exponential function. For the maximum amplitude of the power, the computation is more sophisticated. However, Johnson has shown that the determination of pmaxi and its variance still led to the analytical forms of the integrals. We take from them the following expressions [LAD 99]:
[4.75] 
We easily extract from these two equations the relative uncertainty ε of pmaxi by forming the ratio of the standard deviation [4.75] and of pmaxi:
By using relationship [3.14] expressing the link between the power and the field square amplitude, it appears that the square root of ε gives an indication of the relative uncertainty of the maximum amplitude of the electric field, hence:
We have cautiously adopted the δ symbol, because the numerator of this expression is not strictly similar to the standard deviation of the maximum field amplitude.
As was previously practiced for the random stationary test of the mean field amplitude, the maximum amplitudes will be collected on three polarizations of the probe and on Nc locations on the boundaries of the working volume. The calibration of the maximum amplitude required in the immunity test of electronic equipment will then be found from the estimate of the mean amplitude of these 3Nc maximum field data.
[4.78] 
According to the result given by the central limit theorem, the uncertainty involved by the estimate of this mean will be governed by the normal probability distribution. Consequently, the estimate of the standard deviation of the arithmetic mean in equation [4.78] provide the uncertainty of the mean amplitude of the maximum field component and can be compared to a reference value recommended by the international standard on the reverberation chambers.
4.4.3.6. Discussion on the ratio of the maximum and mean amplitudes
The process has been previously described to evaluate the link between the mean amplitude of the maximums, as is recounted in equation [4.72]. It comes down to purely statistical properties. An alternative and more deterministic point of view consists of examining the maximum amplitudes with respect to mean amplitudes of the standing waves in the chamber.
Let us briefly come back to the field amplitude found in an empty rectangular shaped chamber. We know that when it is excited on an eigenmode, this chamber produces a standing wave, whose field amplitude versus the coordinates x, y, z follows sine functions. Equations [2.46] to [2.55] in section 2.3.2 of Chapter 2 meet this criterion quite well. If we examine the absolute amplitude of a field projection, we find, as a function of one of the three x, y, z variables, a description made up of a series of sine waves patterns. If we consider that Em represents the maximum amplitude of one field projection, the link with the mean amplitude is immediately related by the well-known equation
[4.79] 
Under the conditions of oversized behavior of the chamber generating a random field distribution, we can imagine that the variations of the field amplitude with respect to x, y, z are similar to a sine wave function. The period of this function is set by the emission frequency while the peak amplitude of the sine patterns evolve in a random fashion. This configuration amounts to saying that the amplitude of the maximums are known with an uncertainty which is similar to the σν standard deviation defined in section 3.2.2. Thus, the most significant excursion of the amplitude EM of the maximum will be represented by the sum of Em and σν, i.e.:
Knowing that the mean amplitude of the ideal random field distribution is related to σν by expression [3.32] established in section 3.2.5 and after combination with [4.79], we reach the value of the EM/Emoy ratio formulated below:
We find the factor 2.37, which converted on dB scale gives 7.5 dB. This numerical value seems quite consistent with the experiment, where the ratios observed between maximum and mean amplitude of the data collected during a full rotation of the stirrer are between 7 and 8 dB. We may notice that this evaluation assumes that the random field distribution and the random behavior of the data renewed by moving the stirrer obey the ergodism principle.
4.4.4. Measurements of the quality factor
Some methods are separately or jointly usable for the measure of the quality factor of a reverberation chamber. The method of modal selection will first be examined. This method is not interesting for a chamber operating above the lowest usable frequency fs, but it helps us nevertheless to easily identify the various losses mechanisms in a chamber.
In practice, the measurement of the power balance, which is observed between a transmitting antenna and a receiving antenna, is by far the most frequently used and is really useful for many applications of the reverberation chamber. This process offers the advantage of supplying curves of the quality factor as a function of the frequency.
To conclude this section, we will propose the measurement of the damping time of the reverberation chamber. Its main interest is to directly access the signature describing the establishment of the energy in the chamber.
4.4.4.1. Method of modal selection
The principle assumes the prior localization of the resonance modes. Such is the case of the layout in Figure 2.16 of section 2.4.3. We find in this figure the variation of the power collected on a receiving antenna when the frequency range of emission is close the first eigenmode of the room. With a network analyzer, we measure the S21 parameter versus the frequency. It turns out that this frequency response behaves like a resonant circuit. Figure 4.11 shows its typical signature, as well as the fm n p position of the mode involved.
Assuming the modal response is analogous with the resonant circuits introduced in section 2.2.4 enables us to deduce from the curve of Figure 4.11, the value of the composite quality factor Qg. The value of Qg will be given by forming the ratio between the fm n p modal frequency and the modal bandwidth Δfm n p. Let us recall that the bandwidth is then determined by the 3 dB fall of the S21 parameter:
Figure 4.11. Profile of the frequency response of the S21 parameter attached to a selected mode in view of Qg measurement
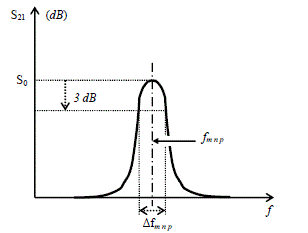
We recall that the composite quality factor Qg involves all losses in the chamber. The use of a field probe, made up of a small antenna with poor antenna efficiency, suits this type of experiment. A trace on a printed circuit placed above a ground plane, may achieve a suitable probe. Since these experiments retrieve variations of amplitudes within a narrow frequency band Δfm n p, knowledge of the transfer function of this small antenna is not necessary. However this method includes the additional losses due to the backscattered power to the transmitting antenna.
4.4.4.2. Power balance method
The power balance method concerns the chambers that are oversized compared to the wavelength. For this reason, the data coming from the measurements will be processed by estimates of data means which are calculated on a rotation of the mode stirrer [SIA 01].
Let us come back to expression [3.135] established in section 3.5.3 and linking the power emission < Ptr > to the < Pcr > power collected on a receiving antenna. If < Ptr > comes from a RF source of frequency f0 connected to a transmitting antenna, the composite quality factor Qg in the denominator of this formula can easily be retrieved from measurements, by forming the ratio < Pcr > over < Ptr >.
[4.83]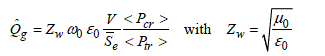 
The volume of the chamber V appears in this equation as well as the impedance of the plane wave Zw and the effective area 
of the receiving antenna. The latter corresponds to the definition of the effective area given in formula [3.132]. Since the use of a weakly lossy field probe does not disturb the power balance in the room, we conclude that the measured composite factor Qg will be almost similar to the quality factor Q1 accounting for wall losses only.
Let us note that, in order to improve the accuracy of the measurements, it is recommended to use the estimate < Ptr > of the power emission rather that the direct measurement of Ptr. Let us not forget that the power emission in the room is expressed in terms of the difference between the power Pt sent to the transmitting antenna and the reflected power from the cavity itself. The later depends on the mode excitation of the cavity mainly governed by the angular position of the stirrer. Another cause of inaccurate data is related to the determination of the antenna efficiency ηe linking Pt and Ptr as given by equation [4.84] but under the assumption of the free space emission. This parameter is generally available in antenna data books. However, measurements of antenna efficiency with a perfect precision are difficult to achieve. This parameter will therefore be concerned by an unknown uncertainty margin.
[4.84] 
The precision of the power measurement may be improved after compensation of the attenuations Ae and Ar. These attenuation coefficients represent the insertions losses of the cables between antennas and instruments. The ratio of the powers appearing in expression [4.83] may thus be corrected. Thus, it will be rearranged according to the notations found in equation [4.85] expressed in dB and in which the attenuations are assessed as positive values:
[4.85] 
In the block diagram illustrated in Figure 4.12 involving a RF generator and a spectrum analyzer, the use of a directional coupler is suitable, in order to collect the reflected power Pρ entering the RF generator.
Knowing that the coupler introduces the attenuation Ac and that the junction cable between the coupler and the antenna produces the attenuation Ae, the power balance deduced from these various equipments is related to the injected power Pi from the RF generator by the following relationship:
Figure 4.12. Insertion of a directional coupler in the emission equipment
4.4.4.3. The damping time-constant method
This method uses the mechanism of the establishment of the energy in the chamber related by relationship [2.64] introduced in section 2.3.6. The use of this formula shows that the 
sine wave amplitude of the electric field vector found in the chamber under the f0 frequency, which is rigorously tuned on the fm n p mode, can easily be transposed in form [4.87]:
[4.87] 
This presentation of the problem assumes that the emission is clearly distinguished from the neighboring modes. We find in this expression the damping constant τ of the chamber, as well as the step function γ(t) specifying that at times lower than zero, the field is strictly null. The function g0(t) governs the maximum (or minimum) amplitudes of the sine wave 
versus the time variable. Therefore g0(t) characterizes the energy expansion in the room and as such will be further analyzed.
The measurement of the expansion response of the room thus immediately gives access to the time constant τ, that we know how to connect to the quality factor of the m, n, p mode by adopting relationship [2.72] recalled below:
[4.88] 
The block diagram in Figure 4.13 summarizes the measuring bench enabling us to display the expansion curve on the oscilloscope.
Figure 4.13. Description of the measuring bench of the damping constant of the chamber
In order to perform periodic repetition of the sine wave emission, the transmitting antenna will be supplied by a RF generator with square modulation whose duration τd will be much higher than the presumed damping constant τ of the room. The period T0 of the square will be much higher than τd.
To obtain the g0(t) expansion response of the room, the voltage collected on the receiving antenna will be rectified by means of a crystal detector. This signal is recorded on a digital oscilloscope, in order to extract the value of τ. We determine then τ from the slope of the curve at t=0, or we solve equation [4.89]:
[4.89] 
Assuming that the receiving antenna obeys a linear behavior, the V0 voltage parameter appearing in [4.89] is rigorously proportional to the 
amplitude of the electric field vector 
As expected, the antennas and other devices contained in the chamber will take part in the various losses that contribute to the time constant τ. Therefore it is directly linked to the composite quality factor, i.e.:
Contrary to the measurements carried out by the power balance method, the quality factor deduced from τ involves the additional damping due to the transmitting antenna.
When the cavity goes into oversized behavior, i.e. supplied with an emission frequency f0 clearly higher than the LUF fs, modal interferences occur within the modal bandwidth Δfg.. This modal bandwidth is directly related to the composite Qg quality factor. These interferences cause modifications of the shape of the transient response g0(t). Experiments show that the shape of g0(t) depends of the angular position θ position of the mode stirrer. This reason leads to equation [4.87] under another notation where vθ(t) represents the voltage collected on the receiving antenna for any angular position θ of the mode stirrer. The amplitude V0 determines then the physical unit (volt) of the formula. g(θ,t) is now an unknown function of the two θ and t variables. This highlights the random behavior of the response shape:
Knowledge of the pg[g(θ,t)] probability density function should lead to the calculation of the moment of g(θ,t), whose result naturally tends to the initial g0(t) function, formulated in [3.86], i.e.:
In practice, this function can only be approximated by the estimate produced on NS angular positions of the mode stirrer, which is releasing independent data, i.e.:
Figure 4.14 shows two configurations of the g(θi,t) response. They are displayed on the oscilloscope according to two independent angular positions θ1 and θ2 of the mode stirrer.
The < g0(t) > estimated mean response is given by the dotted line., It is from this curve that we deduce the value of τ. The distortions observed on the solid lines which are the transient random responses of the room characterize the effects of the modal interferences within the short Δfg bandwidth involved by the composite Qg quality factor.
Figure 4.14. Illustrations related to the various rectified time response of the room submitted to a RF emission
Finally, thanks to relationship [4.88], we reach the estimate of Qg:
The voltage of a few hundred mV needed for crossing the threshold voltage of the crystal detector require us to set up in the chamber a field of several hundred V/m. Let us specify that the RF response of the room can also be detected with the help of a spectrum analyzer.
It is useful to recall that equation [4.87] has been established on the hypothesis of the reduction of the cavity to an assembly of resonant RLC circuits described in section 2.2.4. Strictly speaking, the RF response of the room is mainly composed of many reflected waves on the highly conducting walls of the chamber. Generally, the period T of each reflection cycle will be much lower than the damping time τ of the room. This condition is then quite sufficient to justify the validity of the previous developments.
4.4.5. Localization of the lowest usable frequency of the chamber
Nowadays, there are no recommendations or specific standards devoted to the determination of the lowest usable frequency of the chamber fs. Usually, we consider fs to be five to six times the first eigenmode frequency of the empty room. This situation is certainly explained by the fact that the ideal random field distribution does not appear abruptly once we reach a frequency threshold. This random distribution is rather progressively acquired as soon as the frequency moves away from the first eigenmode of the room.
The data in Table 4.1 of section 4.3.2 which is devoted to mode stirring by frequency hopping restores this property very well. First, we observe the results (the power on a receiving antenna) that correspond to the emission at a frequency below the lowest presumed frequency fs.. Calculated gauge parameters do not systematically come out of the arbitrary threshold. Let us recall that this arbitrary threshold was adopted in order to specify the condition of an ideal random field distribution. To summarize these interesting results, the chamber tested on 11 frequencies centered on 310 MHz gives three tests entering within the threshold gap. Knowing that the presumed fs is about 500 MHz, the experiment proves to be conclusive in showing that fs is confined within an extremely fuzzy range of frequencies. Pursuing the test one octave above fs, i.e. with emission centered on 910 MHz, it appears that two frequencies of the batch still come out of the threshold gap.
From this statement, it seems that the localization of fs based on accurate criteria can be carried out by statistical tests, where the traditional mode stirring and the frequency agitation would be combined. The choice of this process however assumes the prior definition of several criteria, among which we find the selected statistic tool.
Taking into account the prior developments and the desired accuracy, we can aim at the < Δ > mean distance defined in expression [4.44] of section 4.3.1 or at the KS test, which is described in section 3.4.4 of Chapter 3. The first test must be related to a threshold gap and the second with a significance level so-called risk factor, whose characteristics are outside the current standard framework. Let us not forget that the current standards are mainly focused toward the random stationary of the field distribution which requires a consuming time procedure.
The combination of the two other physical parameters will play a decisive part. This is the choice of the central frequencies fa, the sample size of frequencies and the Δfa frequency range adopted to practice the mode agitation.
The choice of fa can only be properly evaluated with the help of the knowledge of the presumed fs. If we except the empirical rule with the factor 5 or 6 brought back to the frequency of the first eigenmode, other choices are also possible. We have pointed out in section 2.4.2 that fs approximately forms the frontier, which leads the stirred volume to be as possible similar as the volume of a modal cell. The configuration reproduced in Figure 4.15 illustrates the main geometrical parameters useful for this confrontation. The stirred volume will be made up of a cylinder with a diameter D and a height h. If we refer to the description in Figure 4.5, h is merged with the height of the chamber.
Figure 4.15. Adjustment of the modal cell on the stirred volume
It remains to determine the ms, ns, ps order of the modal cell made up of the rectangular shaped sub-volume of dimensions D x D x d, in which we can insert the stirred volume. The s index, at the bottom of the m, n, p symbols, means that we aim for the frequency fs. The computation follows the indications of section 2.3.4. If we allocate to the chamber, the a, b and d dimensions respectively projected on the ox, oy and oz axes in Figure 4.15, the order of the modal cell attached to fs must satisfy three equations, stated as follows:
[4.95] 
The symbol ≅ means that ms, ns and ps determine the integers that are the closest to the real values given by equation [4.95].
The evaluation of the lowest usable frequency fs of the chamber is then related by formula [4.1] brought back to the eigenmode frequency with order ms, ns, ps, i.e.:
[4.96] 
For the suggested example, ratios [4.95] are determined for a chamber with dimensions 1.9 m x 2.5 m x 2.8 m and for a stirred volume with a diameter D of 30 cm and a height h of 2.8 m. The calculation leads to the following numerical values [4.97]:
[4.97] 
The presumed lowest frequency fs deduced from [4.96] thus takes the value:
i.e. a frequency close to 700 MHz.
This apparently pessimistic fs finds its explanation in the small diameter of the stirred volume. This also proves that the determination of fs by this approximate method only aims at a rough estimation of the frequency range, where the tests to find fs as described above must be carried out.
The tests combining mechanical stirring and frequency agitation require us to fix the threshold value marking the success rate of the < Δ > parameters or the exit rate of the risk, specified in the KS test. We think that a rate of 50% respects the location of the frontier set by fs quite well.
As an example, Table 4.3 gathers the results of an experiment designed to test a mode stirring improvement device.
Table 4.3. Experimental data illustrating a reduction of fs
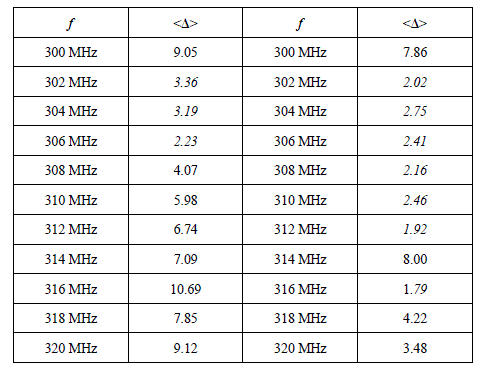
On the left side of the table the values of the < Δ > average distance are expressed in % and recounted for the chamber without stirring improvement. The central emission frequency is located at 310 MHz, i.e. below the presumed lowest frequency of 500 MHz. Frequency agitation concerns a size of 11 samples, which are uniformly distributed in a range of 20 MHz. The data in italics give the values of the mean distance located (under) or close to the threshold gap of 3% which is adopted as the reference value.
On the right side of the table, we find the same data, which are determined after improvement of the mode stirring. The success rate of the test then goes up from 27% to 73%. We can thus conclude that the lowest frequency fs decreased and that it is currently around 300 MHz. Let us specify that the mode stirring improvement device includes two long wires. They are positioned close to the walls of the chambers and we modify their terminations, in order to change the electromagnetic coupling throughout the transmission lines thus constituted. This device is similar to the combination of two mode stirrings mentioned in section 4.3.1.
4.5. Discussion
4.5.1. Regarding the law of large numbers
The use of the statistics is subjected to the principle of the law of large numbers or similarly to the repetition of the trials. In order to reduce the duration of the calibration of a chamber, the standards recommend the collection of samples of data, whose sizes are voluntarily restricted. Such is the case for the selection of the frequencies, for the number of angular positions of the mode stirrer and for the space exploration of the field probe.
This selection is in a direct relationship with the estimate of the mean amplitude taken from equation [4.68] which is established in section 4.4.3. The standards specify that the calibration process is carried out on Nc locations of the probe. These locations are successively moved at the eight corners of the rectangular shaped working volume. Knowing that the probe selects each of the three polarizations of the electric field, we reach a sample size of 24 random data.
According to the stochastic behavior, the sample is clearly undersized, in order to make the rigorously estimated means. However, the reduced size of the random data sample does not compromise the validity of the calibration procedure. Its aim is restricted to the computation of means amplitudes and standard deviation. The latter is compared to an arbitrary threshold gap fixed by the international standard on reverberation chambers. This threshold based on standard deviation includes the concept of uncertainty margin and consecutively the requirement of reproducibility.
The goal is thus quite opposite to the statistical tests adopted in section 3.4.4 of Chapter 3, in order to prove the capability of reverberation chamber to produce the ideal random field distribution. In this context, it is essential that the sample size is large enough as expected by the law of large numbers. A brief recollection of the theoretical simulation produced in Figure 3.4 in Chapter 3 brings a good illustration of the law of large numbers.
4.5.2. On the impact of the volume of the large devices under test
To more accurately and in an empirical manner analyze the physical impact of large devices installed in a reverberation chamber, let us come back to the chamber configured under the geometry in Figure 2.7 of Chapter 2. The rectangular chamber takes the dimensions a = 1.9 m, b = 2.5 m and d = 2.8 m. The a and b sides are the ground floor and d the height. Let us imagine the device made up of a vertical wire of dimension L0 = 2.5 m, put in contact with the conducting ground floor. According to formula [2.56], the first eigenmode frequency of the empty room has been previously evaluated at 80 MHz. The device thus forms an electric monopole, whose short-circuited end meets the criteria described in section 7.3.1 of Chapter 7. The electromagnetic coupling involved by the RF emission within the chamber, will be characterized by the combination of two coupling phenomena.
We first witness a small shift of the first eigenmode of the chamber whose frequency remains close to 80 MHz. Only a numerical calculation by full wave software or a measurement enables us to know precisely this weak frequency shift. However, this small change of the first eigenmode is combined with the monopole’s resonances. Those can be predicted assuming the wire is in free space and connected to an infinite sized ground plane. Later in the book and more especially in section 7.3.1 of Chapter 7, we will see that the first resonance of the monopole occurs, when the dimension L0 of the wire is rigorously similar to the quarter of the wavelength λ. Presently, we find this condition for a frequency of 30 MHz which is about three times lower than the first eigenmode of the empty chamber!
We assume now that the dimension of the device grows in order to reach a rectangular shaped volume with a ground surface of a = 0.9 m x b = 1.5 m and height h = 2.5 m. This metal box then occupies a volume close to 3 m3, i.e. a quarter of the volume of the chamber. As long as the 50 cm gap between the sides of the box and the walls of the chamber remain lower than the wavelength, we find that the room thus filled behaves like a vertical coaxial transmission line short-circuited at the bottom side and opened at the top side.
Using calculations found in section 2.2.2 of Chapter 2, we easily show that the resonance of the device occurs for all the frequencies, so that the L0 dimension is tuned on an odd multiple of a quarter of the wavelength. This simplified approach of the problem leads to the erroneous conclusion that the increasing volume of the device under test enables us to lower the first resonance of the chamber to 30 MHz. This is indeed not the case since the first eigenmode of the filled room is determined by the true volume which remains restricted to 10 m3 against 13 m3 for the empty chamber. The use of a full wave solver to determine the eigenmode frequencies of the filled room is a possible solution to this question.
An increase in the device volume corresponds to a decrease in the composite Q factor of the chamber. Indeed, a decrease in the stored electromagnetic energy is combined with the reduction of the net chamber volume. Furthermore, a larger device impacts the losses which can also contribute to reduce the composite Q factor. The fall of the quality factor of the reverberation chamber reduces the capability of the room to produce high electromagnetic field amplitude and may consecutively influence the stirring performances. Testing large device volumes requires a specific calibration of the chamber.
4.6. Bibliography
[ELH 09] EL HAFFAR M., REINEIX A., GUIFFAUT C., ADARDOUR A., “Reverberation chamber modeling using the FDTD method”, Advanced in Computational Tools for Engineering Applications, Proceedings, p. 151–156, July 2009.
[FIA 09] FIACHETTI C., MICHELSEN B., “Electromagnetic random field models for analysis of coupling inside mode tuned chamber”, Electronic Letters 27, vol. 39, no. 24, November 2009.
[HIL 94a] HILL D.A., MA M.T., ONDREJKA A.R., RIDDLE R.F., CRAWFORD M.L., JOHNK R.T., “Aperture excitation of electrically large Lossy cavity”, IEEE Transactions on Electromagnetic Compatibility, vol. 36, no. 3, p. 169–178, August 1994.
[HIL 94b] HILL D.A., “Electronic modes stirring for reverberation chambers”, IEEE Transactions on Electromagnetic Compatibility, vol. 36, no. 4, p. 294–299, November 1994.
[HIL 95] HILL D.A., “Spatial correlation function for fields in a reverberation chamber”, IEEE Transactions on Electromagnetic Compatibility, vol. 37, no. 1, p. 138, February 1995.
[HIL 02] HILL D.A., LADBURY J.M., “Spatial correlation functions of fields and energy density in a reverberation chamber”, IEEE Transactions on Electromagnetic Compatibility, vol. 44, no. 1, p. 95–101, February 2002.
[JUN 10] JUNQUA I., PARMANTIER J.-P., DEGAUQUE P., “Coupling on cables in an electrically large cavity: a closed-form solution”, IEEE Transactions on Electromagnetic Compatibility, vol. 54, no. 4, pp 1034 – 1040, November 2010
[LAD 99] LADBURY J.M., KOEPKE G., CAMELL D., Evaluation of the NASA Langley Research Center mode-stirred chamber facility, NIST Technical note 1508, January 1999.
[LAL 06] LALLECHERE S., GIRARD S., VERNET R., BONNET P., PALADIAN F., “FDTD / FVTD methods and hybrid schemes applied to reverberation chambers studies”, Proceedings of the First European Conference on Antenna and Propagation, p. 1–6, November 2006.
[LAN 96] LAMBLAIN N., Etude du brassage électronique de modes en chambre réverbérante appliqué aux mesures d’immunité, Thesis, University of Lille, 1996.
[LEF 00] LEFERINK F., BOUDENOT J.C., VAN ETTEN W., “Experimental results obtained in the vibrating intrinsic reverberation chamber”, IEEE International Symposium on Electromagnetic Compatibility, Proceedings, vol. 2, p. 639–644, August 2000.
[MON 08] MONTEVERDE C., KOEPKE G.H., HOLLOWAY C.L., LADBURY J.M., HILL D.A., PRIMIANI V.M., RUSSO P., “Source stirring technique for reverberation chambers: experimental investigation”, EMC Europe 2008, International Symposium on Electromagnetic Compatibility, Proceedings, p. 1–6, September 2008.
[ORJ 07] ORJUBIN G., “Maximum field inside a reverberation chamber modeled by the generalized extreme value distribution”, IEEE Transactions on Electromagnetic Compatibility, vol. 49, no. 1, p. 104–113, February 2007.
[PAP 91] PAPOULIS A., Probability, Random Variables, and Stochastic Process, McGraw-Hill, New York, 1991.
[SIA 01] SI AHMED C., Contribution à l’étude du coefficient de qualité d’une chambre réverbérante à brassage de modes, Thesis, University of Lille, 2001.