Chapter 8
Mode Stirring Reverberation Chamber: A Research Tool
8.1. Introduction
The previous chapters of this book have been devoted to the introduction of the physical phenomena controlling the behavior of reverberation chambers in Chapter 1 through to Chapter 4 and to the implementation of reverberation chambers for radiated immunity tests in Chapter 5 or radiated emissivity tests in Chapter 6 in electromagnetic compatibility, as well as of shielding effectiveness tests in Chapter 7.
The studies developed by many experts throughout the world in the last 20 year shave gathered without a doubt a solid knowledge base today. This results in a henceforth intensive use of reverberation chambers for electromagnetic compatibility tests, throughout the world. Nevertheless, there are still to this day many lines of research on this subject. The discussions concluding the previous chapters present us with some open questions. The physical interpretation of the phenomena involved and the associated theoretical models are still largely discussed. On a very different level, the scope of reverberation chambers also tends to extend itself to different types of electromagnetic compatibility measurements or to other electromagnetic characterizations. The study of reverberation chambers is the object of increasing interest from a growing community of researchers and engineers of various fields. It is thus without a doubt that new reverberation chamber results and approaches will appear in the near future.
The description of the current research studies that deal with reverberation chambers largely exceeds the objectives of this book. We will however take a more particular look at the observation of the non-ideally random field distribution, as it is observed in practice. The ideal random field is indeed the primary assumption of this book and it seems quite important to compare it to the results of the experiment, so that we manage to detect a possible departure from the ideal statistical behavior, and above all to evaluate the impact on the statistical uncertainty margins.
Continuing on from the previous reasoning, we will come back to the question of stirring effectiveness, which is transposed in the observation of the correlation of the random data collected during an experiment. The capture of non-correlated data is not necessarily synonymous with their statistical independence. It is well established from statistical theory that a sample of uncorrelated data, according to the definition of a correlation function, may be composed of dependent data in some way. This chapter will cover this matter in greater depth. This chapter will then conclude with the subject of measuring the fraction of the coherent wave, resulting from a direct excessive coupling with the transmission antenna or from an insufficiently efficient stirring.
These illustrations evidently represent only a small part of the research studies currently carried out on the subject of reverberation chambers. Indeed, some points barely touched upon in this book have been and still are the subject of careful studies. Such is the case for the calculation of the field distribution in a chamber addressed by time domain simulation in 3D, for instance with the help of the finite differences method. Some of these calculation techniques have also been recounted in some works written in the past decade [HOE 01, PET 02] and are still an important research matter [PRI 09]. Finite element techniques in steady state have also been investigated [BUN 02]. Control of the calculation of the field distribution in a chamber can significantly help designers and practitioners to understand the impact of the most fundamental parameters. We need to point out on this subject that determination of the dimensions and of the geometrical form of a mode stirrer can come within the field of a simulation process, where hybrid calculations are involved. Convincing results have been recently obtained on this question [LAL 06].Improvements of the numerical simulation can also lead to a comparison of the calculated and measured field distributions.
Evidently, these calculations can only be suitably developed after the introduction of the main parameters controlling the functioning of the chamber, such as the composite quality factor of the propagation modes. An alternative approach to the exact calculation consists of solving Maxwell’s equations with the introduction of random behavior parameters. The stochastic collocation method (which is a spectral method aiming at minimizing the number of simulations required by the conventional Monte Carlo process) has been used quite successfully by allocating the role of the virtual random variable to the conductivity of the walls. The probability density function of this virtual variable is then linked to the random variable under investigation, which is attached to the evolution of the electric field in the chamber [DIO 08]. This same process can be used in order to evaluate the radiation of an electrically conducting wire placed in a reverberation chamber. The Green functions accounting for the radiation of the wire are then connected to the evolution of the electric field [DIO 07]. Other approaches aim at building the plane wave spectrum, which is allocated to a field distribution calculated beforehand by a numerical method [NAF 09]. Here we can measure the impact of these studies and their powerful connection with the assumptions formulated on the generation of an ideal random field, as depicted in the previous chapters of this book.
To conclude this introduction, let us briefly come back to the aspects developed in this chapter. In the current state of theoretical studies carried out on the question of the operation of reverberation chambers, the model of the random plane wave spectrum satisfactorily explains the observed behavior in a well oversized cavity,despite the simplicity of the initial assumptions. The random plane wave spectrum relies on the hypothesis of the successive generation of a high number of modes provided by the action of the mode stirring. If the geometrical shape of the cavity is assumed to be a sphere, polarization and angle of incidence of incoming plane waves are therefore uniformly spread. As justified by some recently fulfilled studies,this representation described in Hill’s model has its own limits [FIA 05].
On the other hand, some departure with regard to the ideal random field distribution can also be revealed using experimental procedures and statistical analysis tools, always better adapted to the context of the reverberation chambers[ARN 02, LEM 07, ORJ 06]. Consequently, this imposes new approaches, enabling us to examine the behavior of reverberation chambers in the frequency ranges,where they are supposed to move away from the model of the ideal random field.
The question of the number of independent realizations collected during the stirring process is also discussed in section 8.3. Indeed, collection of the complete sample must be in principle made up of individual data that are all independent from each other. In practice, we detect a possible dependence with the help of a linear correlation operator. If we estimate this linear correlation close to zero, it is not sufficient to demonstrate the independence of the measurement data. In fact, other correlation forms are possible. On the contrary, the observation of linear correlation authorizes us to state that the sample is not a set of fully independent data. An analysis of the efficiency of this stirring process may therefore be carried out. In particular, this analysis provides an interesting observation to evaluate the consequences on the statistical uncertainty budget of the measurement.
In addition, as we have already pointed out in this book, the use of reverberation chambers is no longer limited to the EMC applications. We could not conclude this book without illustrating some recent studies on the application of the reverberation chambers. We will focus on their ability to measure antenna characteristics in specific situations. In particular, we examine the simulation of a controlled electric field distribution, other than a Rayleigh distribution, in order to evaluate the performance of combined multiple antennas.
This chapter is only an introduction to several research studies showing on the one hand that the questions relative to the theoretical or behavioral analysis of the reverberation chambers are not all solved and on the other hand that the domain of the investigations and applications does not stop increasing.
8.2. A non-ideal random electromagnetic field
The assumption of the ideal random field amounts to considering that the angle of arrival and the polarization of the incident field at the observation point are uniformly distributed. This is only possible when a sufficient number of resonant modes are excitable during the rotation of the mode stirrer.
In an equivalent way, in the assumption of small wavelengths compared to the dimension of the cavity, the almost optical hypothesis enables us to give an account of a propagation model, in the form of plane waves with multiple routes in the chamber. These routes are strongly altered by the rotation of the stirrer. A perfectly balanced distribution of incidence angle and polarization, in the meaning presented above, is only strictly possible if the cavity has symmetry properties. This is the case for a cavity of spherical form.
In practice however, most of the chosen Faraday cages are rectangular shaped.This geometry can lead to the non-uniformity of the angular distribution of the plane wave spectrum, which is created in particular if the parallelepiped cavity is very asymmetric. On the other end, in the frequency spectrum close to the lowest functioning frequency, the mode density is not so high as to require an ideal behavior. In this context, the number of degrees of freedom allowed by the stirrer is limited. Therefore, these factors may invalidate the assumption of uniform probability of the angles of arrival and/or of the polarization of the incident fields.
On an experimental level, it is possible to highlight the departure from the ideal behavior, even when it is weak, in comparison to the Rayleigh process, which is attached to the electric field modulus, by using a specific analysis of the statistics of the data recorded during a mode stirring process. This analysis can be carried out with the help of a statistical goodness-of-fit test, relying on the well-established statistical theories, as introduced in Chapter 3 of this book.
8.2.1. An estimate of the statistics of a rectangular component of an electric field in an effective reverberation chamber
8.2.1.1. Estimate of the Rayleigh distribution parameter
We saw in Chapter 3 that in the context of the production of an ideal random field distribution, on any field projection, measured with the help of an electric field probe, a rectangular component follows a Rayleigh distribution. We recall here its probability density function:
[8.1] 
The expression used here conforms to the Rayleigh process given for a normalized variable of type u = ER / σv (expression [3.28] of Chapter 3), where σv is the standard deviation of the normal distribution. The latter underlies the behavior of the complex real and imaginary components of the random field.
We recall that the mean and standard deviation of this random variable are respectively given by:
[8.1a] 
[8.1b] 
The Rayleigh distribution function is a random process, more frequently described by the statisticians in a form adapted to its analysis, via the introduction of variable change θ = 2σ2 . The corresponding probability density function is easily deduced from [8.1], in the form:
[8.2] 
Hence:
[8.3] ![]()
[8.4] 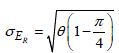
The Rayleigh distribution written in this form thus depends on the single parameter θ, whose value need to be estimated beforehand. This estimate is done with the help of a series of measurements, each corresponding to an individual realization of the random variable. This estimator which we note ![]() is also a random variable. Consequently, the quality of this estimate depends on appropriate choice for the estimate function, whose objective must be to minimize the probability of the estimate error. Generally the maximum likelihood method [PAP 02] is used to determine this function. Its application to the normal distribution is illustrated in Chapter 3. This estimate function closely depends on the underlying probability density distribution of the random variable. In this case it is the Rayleigh distribution. The maximum likelihood is expressed as the maximization of the likelihood function, as it is presented in section 3.4.3 of Chapter 3. From a sample of the random X variable composed of N individual measurements (x1,x2,…,xN), we seek the best possible estimate
is also a random variable. Consequently, the quality of this estimate depends on appropriate choice for the estimate function, whose objective must be to minimize the probability of the estimate error. Generally the maximum likelihood method [PAP 02] is used to determine this function. Its application to the normal distribution is illustrated in Chapter 3. This estimate function closely depends on the underlying probability density distribution of the random variable. In this case it is the Rayleigh distribution. The maximum likelihood is expressed as the maximization of the likelihood function, as it is presented in section 3.4.3 of Chapter 3. From a sample of the random X variable composed of N individual measurements (x1,x2,…,xN), we seek the best possible estimate ![]() . In other words, we try to find
. In other words, we try to find ![]() such that its probability density function is the highest possible around the reference (true)parameter θ. This amounts to maximizing the PN probability density function,which corresponds to the accumulation of N trials of the random variable given by:
such that its probability density function is the highest possible around the reference (true)parameter θ. This amounts to maximizing the PN probability density function,which corresponds to the accumulation of N trials of the random variable given by:
[8.5] 
Similarly to the approach presented in Chapter 3 for the normal distribution, we look for the solution in the form of vanishing the derivative of the natural logarithm of the probability density PN. We thus show that the estimator with the maximum likelihood for the Rayleigh distribution is governed by:
[8.6] 
We thus easily deduce the following result for the sought after estimator:
[8.7] 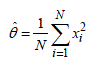
The ![]() estimator with the maximum likelihood for a Rayleigh distribution thus represents the mean square of N realizations of the analyzed random variable.
estimator with the maximum likelihood for a Rayleigh distribution thus represents the mean square of N realizations of the analyzed random variable.
8.2.1.2. The goodness of-fit test for a Rayleigh distribution with an a priori unknown parameter
We saw in Chapter 3 and more particularly in section 3.4.4 that we frequently used the Kolmogorov-Smirnov test, in order to evaluate the distribution of a collection of data resulting from a random process with continuous values. The analysis of the data resulting from the mode stirring in reverberation chambers is very often carried out with the help of this test. The result of this statistical adjustment test is generally compared to the Massey table (see Chapter 3 and [MAS 51]). As also highlighted in section 3.4.4, the selection of the critical values of the Massey table is only appropriate if we consider that the parameter of the distribution to be tested is known before hand and does not need to be estimated.
This is evidently not the case for samples of measurements in reverberation chambers, for which we need to previously estimate the parameter(s) of the supposed underlying distribution of the random variable. We have seen above in particular how to estimate the θ parameter of the Rayleigh distribution for a rectangular component of the electric field.
Statisticians have provided sets of critical values or other test methods enabling us to check the fit of various statistical distributions, specifically in the case where this preliminary estimate of the parameters is necessary.
In the case of the Kolmogorov-Smirnov test, Lilliefors [LIL 67] and Stephens[STE 74] have developed new tables according to a process similar to the one used by Massey, for an exponential distribution and also valid for a Rayleigh distribution.The process of establishing these tables can for example be based on the simulation of a large number of samples of N values of the considered probability distribution function. For each one of these samples, the estimate of the most likely value of the parameter(s) is carried out. The large number of samples leads to the convergence(Monte-Carlo method) on the distribution of the deviations D, between the theoretical distribution function and the empirical distribution function. The chosen confidence interval then gives the critical value.
Thus, the table developed according to this process by Stephens for the test of an exponential distribution or a Rayleigh distribution, is very useful for the analysis of the measurements of power and electric field components which are carried out in reverberation chambers. We seek to precisely evaluate if the power is of exponential type and if an electric field projection follows a Rayleigh distribution.
We give in Table 8.1 the Stephens table, whose values are compared to the Massey table, for different values of N.
We recall that the statistical gauge of the Kolmogorov-Smirnov test is given by:
[8.8] ![]()
where SN (x) is the empirical distribution function of the (x1,x2,…,xN) elementary s measurements, and Fth(x) is the theoretical cumulative distribution function to be tested. The critical distance Δc indicated in Table 8.1, are the values that the statistics Δm must not overcome for a given significance level α. The assumption of adjustment to the distribution is considered as accepted, for Δm<Δc(α) with an significance level that corresponds to α%. In the opposite case, the distribution is considered to be rejected. Let us recall that α would correspond to the probability of overcoming the critical value, assuming the random variable strictly complies with the tested distribution function.
Table 8.1. Massey and Stephens critical distance values for different values of N
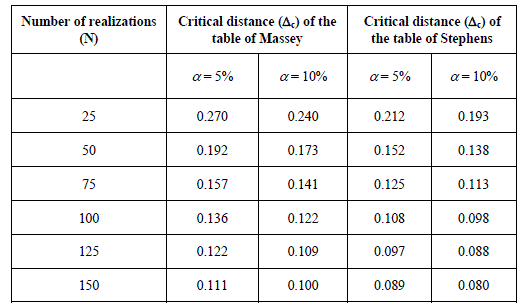
Observation of Table 8.1 leads to two conclusions. On the one hand, the critical values given by Stephens are lower than the critical values of Massey, whatever the size of the considered sample. Concretely, this means that the Kolmogorov-Smirnovtest is, according to the Stephens criterion, stricter than the test according to the Massey criterion. This is not surprising considering the bias system atically introduced by the initial assumption by Massey, related to the preservation of the distribution parameter from one sample to another. On the other hand, the difference between these critical values may seem to be weak.
Consequently, this means that the Massey table, although wrongly used,indicates if the Rayleigh assumption (or the exponential one) is a reasonable assumption. Let us note that the result of the test does not mean at all that the process follows the tested distribution with certainty, but that it is acceptable.However, the Stephens table is a stricter test, likely to move away from the Rayleigh assumption (or the exponential one) more easily, if the collection of the data to be tested drifts even slightly from the expected distribution.
To be more exhaustive, the Stephens critical values applied to the Kolmogorov-Smirnov test for any number N are given for several significance levels within Table8.2, where the critical value V is given in the form of an analytical function of the N number of realizations and the statistical gauge Δm, which is always calculated according to expression [8.8]:
[8.9] 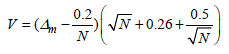
Table 8.2. Stephens critical values for any sample size N for the goodness-of-fit-test of an exponential distribution also applicable to a Rayleigh distribution

In the following, we will introduce a comparison of these two tests (Massey and Stephens) on the same series of measurements in reverberation chambers.
8.2.1.3. Example of the Kolmogorov-Smirnov test according to the Massey and Stephens criteria from measurements carried out in a reverberation chamber
The measurements presented here are carried out in a reverberation chamber,whose approximate dimensions are 8.7 m in length, 3.7 m in width and 2.9 m in height. The experiment is carried out with the help of a log-periodical-type transmission antenna, which is directed towards the stirrer of the chamber, in the frequency band of 200 MHz to 1,100 MHz. The field probe used is a tri-axial probe,enabling us to simultaneously measure the three orthogonal projections of the field.Its dimension is much lower than the lowest working wavelength.
In order to evaluate the rejection rate of the Kolmogorov-Smirnov test, we cannot reach a conclusion with the help of only one sample of N realizations.According to the choice of the significance level, we must indeed have at our disposal a significant number of these samples. This is naturally a difficulty,because, on the one hand, we need to multiply the measurements in reverberation chambers, and on the other hand, we need to ensure the non-correlation of the measurement conditions. The study of the correlation is an important preliminary checking stage. We will admit in the following that all the necessary precaution shave been taken in order to ensure the absence of correlation of the collected observations. This is indeed a difficult matter that we will come back to in section8.3 of this chapter. The experiment relies here on a set of measurements in various arbitrary positions of the probe, which are sufficiently spaced from one another in order to minimize spatial correlation of fields. Moreover the large mechanical stirrer is rotated in several positions with a rotating step angle big enough to reconfigure the standing wave pattern in the chamber. Preliminary tests confirm that the set of data thus collected exhibit a weak linear correlation. In total, we have at our disposal a minimum of 18 samples of size N = 150 up to the frequency of 400 MHz, and 30samples above 400 MHz. This limitation of the number of samples in the low frequency range of measurements is explained by having at our disposal a more limited number of stirrer positions, leading to a correlation of the measurements,which are estimated as negligible. The goodness-of-fit test of the Rayleigh distribution is carried out on all the 18 or 30 collected samples, for which the statistical margin Δm is evaluated. The rejection rate corresponds to those samples for which a statistical margin exceeds the Massey or Stephens limit values and gives quite a good idea of the acceptability degree of the distribution. It remains to naturally fix the level of significance α, enabling us to select the corresponding limit values. We set, in a conventional but arbitrary way, α= 0.05.
Figure 8.1 gives the rejection rates associated with the Kolmogorov-Smirnovtest, according to Massey and Stephens. For every frequency of this test (200 to1,100 MHz per step of 100 MHz), the two values are compared with the help of two histograms. These histograms highlight the strictness difference of the two tests. At200 MHz, the two tests massively reject the Rayleigh distribution. The electromagnetic cavity seems to be insufficiently oversized. Beyond 700 MHz, the two tests seem to greatly accept the assumption of the Rayleigh distribution. There is between 200 and 700 MHz a transition zone, for which it seems that the test according to Stephens rejects the assumption of Rayleigh distribution, whereas the test according to Massey is far more positive. It is important here to indicate that a conventional standardized test, such as those presented in Chapter 5 of this book,gives a lower usable frequency of about 250 MHz for this chamber. Stephens’ test clearly indicates that despite the fact that the conditions are met so that the chamber may possibly satisfy the requirements of statistical uniformity level; the process does not quite faithfully follow a Rayleigh process which is only reached in reality in a very significant oversizing regime.
To confirm this assumption, we then need to seek an underlying distribution,which could be a better candidate than the Rayleigh distribution for the data experimentally observed. Ideally, such a hypothetical distribution would have a less stringent condition in order to fit with the data set. A possible solution is to seek a multi-parametric solution. The family of the Wei bull distributions owns this characteristic, as well as the advantage of integrating the Rayleigh distribution(this means the χ distribution with two degrees of freedom) and the exponential distribution (this means the χ2 distribution with two degrees of freedom).
Figure 8.1. Histograms of the rejection rates in % for the Kolmogorov-Smirnov test of a Rayleigh distribution for an electric field projection. The two columns per frequency correspond to the calculation of the rejection rate according to the application of the Massey criterion (black hatched) or of the Stephens criterion (gray border)

8.2.2. Resorting to a replacement distribution: the Wei bull distribution
8.2.2.1. The Wei bull distribution with two parameters
Resorting to a Wei bull distribution with two parameters [JOH 94, WEI 51] is considered here in order to describe the behavior of the reverberation chambers in the regime of a non-ideal random field. The probability density function of this distribution is given by:
[8.10] ![]()
In this equation, a and b are real parameters. The a parameter is called the scale parameter, and b is the shape parameter.
By identifying the Rayleigh distribution given in the form of [8.2] with probability density function [8.10], we easily show that the Wei bull distribution is similar to the Rayleigh distribution, for the following values of a and b:
[8.11] ![]()
If the measurements have been normalized beforehand, that is to say brought back to their mean value, we can show that a = π /4 .
8.2.2.2. Estimate of the parameters of the Wei bull distribution
In order to compare our set of measurements to the Wei bull distribution, we also need to optimally estimate the parameters of this distribution. For this, we also resort to the method of the maximum likelihood. The PN,Wei bull probability function for N trials of a Wei bull random variable is written in the form:
[8.12] 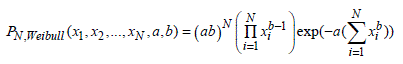
By taking the logarithm of expression [8.12] and by calculating the partial derivatives with respect to both a and b parameters, and then by seeking the values of a and b, for which these partial derivatives are cancelled, we then obtain the following system of equations:
[8.13] 
The pair of estimated parameters (a,b) is thus the solution of this system of equations, which are formed from the (x1, x2,…, xN ) sample of measured values. From this estimate of the parameters of the Wei bull distribution, we classically carryout a statistical goodness-of-fit test.
8.2.2.3. Goodness-of-fit test of the Wei bull distribution and associated critical values
The test of a Wei bull distribution can also be carried out with the help of the Kolmogorov-Smirnov method.
However, critical values of Table 8.2 are not valid in the specific framework of the Wei bull distribution. The critical values of the Wei bull distribution have been otherwise determined [EVA 89] and we directly transpose the result in Table 8.3.
Table 8.3. Critical distance for the Kolmogorov-Smirnov test of a Wei bull distribution with two parameters

8.2.2.4. The Wei bull distribution applied to measurement data in reverberation chambers
We have noticed above that the behavior of the measured data (in this case an electric field projection along any axis in reverberation chamber) did not perfectly answer the assumption of a Rayleigh distribution on the entire frequency band under investigation. The objective of the analysis proposed in this section is to evaluate if the Wei bull distribution would be suitable for the description of this behavior.
This is thus the same set of data as in section 8.2.1.3, which will be subjected to this new statistical goodness-of-fit test.
The result corresponding to this analysis is represented in Figure 8.2. We show the rejection rate of the Wei bull distribution by comparing it to the rejection rate previously calculated for the Rayleigh distribution.
Two tendencies are clearly emerging when consulting histograms. Beyond700 MHz, the rejection rates are comparable for the two distributions. This result corresponds with one’s expectation. Indeed, the Rayleigh distribution is a Weibull distribution of parameters a = 1/θ and b = 2. The Wei bull test only confirms the result of the preliminary test about the Rayleigh distribution. The values of the a andb parameters, estimated with the help of relation [8.13], give us information about the shape of the probability density of the distribution and notably about its deviation with regard to a Rayleigh distribution.
Figure 8.2. Histograms of the rejection rates in % of a)the Kolmogorov-Smirnov test according to Stephens criterion for a Rayleigh distribution (gray hatched); b) the Kolmogorov-Smirnov test of a Wei bull distribution (black hatched). Data are measured amplitudes of an electric field projection

The second observed tendency corresponds to a very clear discrimination of the result of the two tests, for frequencies lower than 700 MHz. Indeed, we notice that while the Rayleigh distribution is massively rejected, the Wei bull distribution is on the contrary widely accepted. We can thus conclude that the Wei bull distribution more suitably describes (than the Rayleigh distribution) the behavior of this reverberation chamber, when we analyze the measurement results in terms of the rectangular component of the electric field measured with the help of a field probe.This does not mean that any other distribution can be an even better candidate.Failing to determine a better prospect, the aforementioned at least fits the measured data better than the Rayleigh distribution.
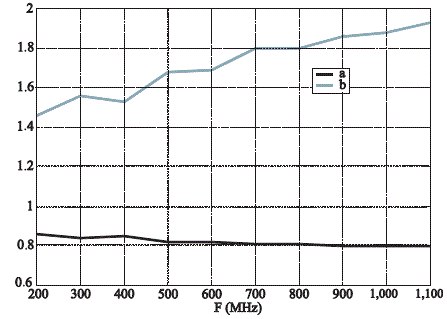
The a and b parameters of the Wei bull distribution are estimated for each frequency multiple of 100 MHz, for which the measurements have been carried out.The corresponding layout appears in Figure 8.3. We notice that by progressively increasing the frequency, we get closer to the Rayleigh distribution. This tends to show that the chamber is progressively idealized with the rise in frequency, as predicted by the theoretical analysis of the reverberation chambers presented in Chapter 4 of this book. We are referring here to the limited mode density found in a not much oversized chamber in its lowest frequency band of operation. This probably, as consequence, moves us a little away from the model of the perfectly uniform plane wave spectrum. This represents however an assumption to be confirmed, either on a theoretical basis or on a modeling method.
Figure 8.3. Estimate of the a and b parameters of the Wei bull distribution, corresponding to the measurements of an electric field projection in reverberation chamber
In practice, more precisely recognizing the random behavior of a reverberation chamber can enable us to better control the uncertainty of measurements carried out during the estimate of any physical parameter in a reverberation chamber. This estimate represents either a moment of the underlying distribution or a function of moments of this distribution. The standards of electromagnetic compatibility in radiated immunity (see Chapter 5 of this book) relies for example on the calibration of the electric field measured with the help of a probe.
There is however another important criterion in terms of the analysis of the stochastic behavior of a reverberation chamber: the non-correlation of the important collected observations, which form the analysis sample suitable for the study of the goodness-of-fit tests. However, in practice, this matter deserves our attention,because deciding or not on the correlation of a series of measurements is in realitydifficult.
8.3. Studying the correlation of a set of measurements
Up until now, we have deliberately set ourselves in the case where the measurements could be considered to be non-correlated in the meaning of the correlation operator used in section 8.3.2 below. This correlation measurement is infact the most frequently used by the standard documents. It is indeed planned that the stirring process used is previously the subject of a check of the absence of correlation. We take a more particular look at this (seemingly) simple evaluation process, but as illustrated below, it leads to an impact on the quality of the measurements carried out.
8.3.1. Outline of the link between correlation and statistical uncertainty
The question of statistical tests is useful to check which theoretical distribution best fits the data. Nevertheless, whatever the underlying distribution concerned, the possible correlation between the different observations concretely manifests itself as an increase in the measurement uncertainty. Any electromagnetic test indeed in reverberation chamber requires a collection of data, through a stirring process, and these are possibly, at least partially, correlated. Precisely evaluating its impact must go through an evolved statistical analysis, whose outlines will be given here. To understand the nature of the relation between correlation and measurement uncertainty, let us observe two different situations.
First, let us assume that we collect N non-correlated and independent measurements. If we seek to estimate the moment of this series, this estimate is a random variable, which asymptomatically strives (i.e. N is high enough to apply the law of large numbers) for a normal distribution centered around the true mean value noted Norm (μ,σ/![]() ), where μ and σ respectively represent the true mean value and the rigorous standard deviation of the underlying probability distribution [PAP 02]. The result is that the committed uncertainty is directly linked to the 1/
), where μ and σ respectively represent the true mean value and the rigorous standard deviation of the underlying probability distribution [PAP 02]. The result is that the committed uncertainty is directly linked to the 1/![]() factor, if the resulting measurement observation is the mean estimate of themeasurements.
factor, if the resulting measurement observation is the mean estimate of themeasurements.
Secondly, we admit that our stirring process is very much imperfect and that it leads us to collect measurements that are pairwise correlated. In other words, the recorded sequence (x1,x2,…,xN) is such that the correlation between the ith element is total with the i+1 element and non-existent with the i+2 element,whatever the value of i. In an extreme situation, the initial sequence could become very close to the double collection of N/2 data. In that case, the first moment strives for a normal distribution centered on the true mean noted Norm(μ, σ /![]() . This estimate naturally includes a more significant uncertainty.
. This estimate naturally includes a more significant uncertainty.
In reality, these extreme situations are not found in practice and the correlation between successive observations is partial, for example in the meaning of the neighboring positions of the mode stirrer. We thus need to determine if this correlation is sufficiently low so that we reasonably consider that the series (x1,x2,…,xN) of measurements really gives N non-correlated data. We need to specify here that the non-existence of a correlation is a necessary, but insufficient,condition to prove independence between sample data. We will thus only be able to postulate that the measurement independence is then a possible assumption in a case of non-correlation.
8.3.2. Measurement of the correlation
The correlation is in reality a statistic carried out from the study of two series of observations X (x1,x2,…,xN) and Y(y1,y2,…,yN). The most frequently used operator relies on the detection of a linear correlation. Although there are many possible formulations of such an operator, the Pearson statistic is used for the measurement of the linear correlation, given by:
[8.14] 
In this expression, the denominator is in reality a normalization coefficient. Let bbe a real and constant parameter. Thus, if the (x1,x2,…,xN) and( y 1, y2,…,yN) series co-vary in an identical way (yi = xi+b) or in an opposite way (yi = -xi + b), then the coefficient will be respectively equal to 1 or -1. It will take an intermediate value for any other situation. This statistics enables us in fact to detect the existence of a relationship between the parameters of the Y series and the X series, in the form of the linear function:
[8.15] ![]()
The a parameter indicates the direction of a regression line which we determine from all of the covariances of the pairs (xi , yi). Without any tendency, no regression line can adapt itself to this set of points which in this case is randomly spread in thex-y plane. For two samples of infinite size not linearly correlated, the correlation coefficient is null. This is the result of the absence of linear correlation, but does not presume of any other form of non-linear correlation.
The literature points out other correlation statistics, which are adapted to various forms of non-linear correlation. However, in the context of application to the reverberation chambers, the linear correlation operator has proven to be an efficient correlation detector for a series of observations corresponding to consecutive positions of a mechanical stirrer or to step by step modifications of the RF source frequency in the chamber. Nevertheless, caution is advised concerning the ability of such simple statistics to detect more complex correlation forms. From an estimate of the correlation coefficient, it remains nevertheless to detect a decision criterion likely to confirm the assumption of non-correlation of the collected measurements.
8.3.3. Study of the linear correlation during experimental estimates
In order to detect possible correlations within a single series of measurement X(x1,x2,…,xN), we can replace Y in expression [8.14] by the same series of values,which are translated or permuted at the p order, where p is a natural integer to form the sample (xp, xp+1,…,xN-p,…). The translation corresponds to an acquisition carried out during the time or during a movement in the space. We then study the porder auto correlation of the sample X.
The first order auto correlation coefficient is calculated from the virtual Y sample, so that:
[8.16] ![]()
The second version of expression of Y on the right side of [8.16] can be meaningful when it is for example a uniform rotation step of a mode stirrer on a complete rotation. In that case, the angular incrementation of the stirrer is indeed identical between the xN and x1 measurements on one side, and between the x1 andx2 measurements, on the other side.
We will note later p(X,X+1) the first order auto correlation coefficient, which is obtained by a shift or rotation of one row of the series of measurements. However,the p(X,X+1) correlation coefficient thus determined, must enable us, possibly from only one sample, to diagnose the absence or the presence of the correlation. At this stage, two difficulties occur. On the one hand, the first order correlation coefficient is evidently a random variable, from which we can only hope at best for an estimate, whose precision will be limited by the sample size N. On the other hand, we also need to set a reasonable critical threshold of p(X,X+1), below which we can reasonably formulate the assumption of the absence of correlation.
In the context of the existing standards [IEC 02, RTC 07] on the reverberation chambers, the chosen convention consists of fixing, whatever the value of N, the critical threshold below which we admit the linear non-correlation at:
[8.17] ![]()
This value corresponds to the approximate value of the result of the exponential function of -1. This threshold is very frequently used. We cannot however particularly justify this choice in the analysis of the correlation of the measurement sin reverberation chambers.
In reality, we should not pay too much attention to it. Section 8.3.4 highlights this, studying the statistical behavior of the estimate of p(X, X+1) from an experimental measurement.
8.3.4. Statistical distribution of the coefficient of linear correlation
Indeed, let us assume that a sample of size N subjected to our correlation analysis is not correlated. In this case, we can expect that the evaluation of p(X, X+1) is such that this value would be close to 0. If we have at our disposal an infinite sample of uncorrelated data, then the expected value given by expression [8.14] will indeed be null. It is particularly useful to know the properties of the p(X, X+1) estimate as a function of the number N and of the true value of the correlation of the collected sample.
Let us assume that the moment of the auto correlation function of the random process observed is such that E(ρ(X,X+1)) = ρ. If we had at our disposal an infinite sample of correlated realizations, this function would tend to this value. Letr be the estimate of the first order auto correlation function, carried out from a sample of limited size N. We can show that the ψN(r) probability density function of the correlation coefficient of a process, for which the expected value of the correlation is such that E(ρ(X, X+1)) = ρ for a sample of size N, is put into the form [KRA 05]:
[8.18] 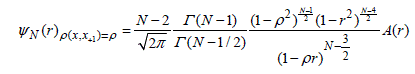
with ![]()
An almost perfect estimate would give an almost certain probability of findingr = ρ. In practice evidently, a particular estimate of r may be more or less distant from the true value p, according to pdf [8.18]. In reality, the larger is the sample size N, the higher is the probability that the estimate will be closer to the true value. It results that the 0.37 set threshold must be interpreted differently according to the sample size under investigation [KRA 05, LUN 00].
To convince ourselves, we draw in Figure 8.5, the curves of probability density function [8.18], with N = 30 and N = 300, for a series of measurements entirely non-correlated (p= 0). It is easy to calculate from these curves the probability of obtaining specific ranges of values for r. Thus, we take a look at the ![]() probability; which corresponds to the probability of estimating an absolute value of r greater than ρt, although the sample is not correlated at all. This probability is given by:
probability; which corresponds to the probability of estimating an absolute value of r greater than ρt, although the sample is not correlated at all. This probability is given by:
[8.19] 
A quick observation of the two probability density curves in Figure 8.5 very clearly shows that this probability for ρt =0.37 is extremely low for N = 300. Indeed,the area under the curve sections corresponding to values of autocorrelation coefficient lower than -0.37 and higher than 0.37 is very small. In reality, for N = 300, the probability to extract a correlation coefficient of about 0.37 from a series of null correlation measurements is minimal. This means a contrario that if the calculation of the first order auto correlation function yields a higher absolute value than 0.37, it is then almost certain that the measured series is at least partially correlated.
For N = 30, this probability of obtaining a correlation estimate higher than 0.37is much more significant. Indeed, this probability is about of 5%. The correlation estimate on a sample of small size, although made up of non-correlated implementations, is indeed less reliable. In this specific context, the threshold of0.37 specifically corresponds to the 5% significance level of making an interpretation error. This significance level is commonly adopted as a trade-off between strictness of evaluation and possible misinterpretation of results for very small values of significance level, Therefore, the 0.37 limit may sound reasonable for N=30.
The example carried out for two sizes of samples shows very simply that testing the 0.37 threshold does not have any general meaning and that it cannot in reality lead to an evaluation of a specific correlation level. It is thus interesting to seek an alternative for this estimate.
Figure 8.4. Probability density function of the auto correlation function estimate for a sample whose true correlation value is null. This probability density is given for two sample sizes representing a series of N = 30 or N = 300 realizations of the considered random variable

8.3.5. Approximation of a normal distribution for the estimate of the first order correlation function
Observation of the curves in Figure 8.4 lets us think that function [8.18] could be approximated by a simple function. In reality, we can show that for values of plower than about 0.5, the pdf of the auto correlation function is comparable to a normal distribution of type Norm(ρ,σρ), with σρ, the standard deviation of this normal distribution and ρ, its expected value. We can show that:
[8.20a] ![]()
with:

or else in its analytical form:
[8.20b] 
This approximation, even valid for correlation values lower than 0.5, turns out to be useful in the context of the analysis of measurements in a reverberation chamber,which most of the time have correlation values smaller than this threshold. Beyond this threshold, the approximation of the normal distribution is less reasonable. This approximation is useful for trying to determine the correlation coefficient of a series of measurement with a reasonable estimate uncertainty.
In the following, we will assume that correlation coefficient is always positive,without loss of generality of the result. We estimate ![]() according to expression [8.14] from N measurements, which are collected during the rotation of the stirrer.The angular position of the stirrer is thus the subject of the analysis of the probability distribution of the field in the chamber, or in other words it is the probability space under investigation. We set as a target the determination of the probable interval [pinf, pup] of the estimate of the correlation coefficient.
according to expression [8.14] from N measurements, which are collected during the rotation of the stirrer.The angular position of the stirrer is thus the subject of the analysis of the probability distribution of the field in the chamber, or in other words it is the probability space under investigation. We set as a target the determination of the probable interval [pinf, pup] of the estimate of the correlation coefficient.
First, we take a look at the determination of pinf, as representing the lower bound of the correlation coefficient. Let pinf be the expected value or the true value of the auto correlation function. According to assumption [8.20a], we can write that the estimate of pinf follows a normal distribution, noted Norm(pinf,σpinf), whose mean value is pinf and standard deviation is σping . Thereupon, we can seek pinf ,so that the two following conditions are respected:
[8.21a] ![]()
[8.21b] ![]()
Relation [8.21a] expresses the estimate of the correlation function when its expected value is indeed pinf. Expression [8.21b] conveys the research for a probability threshold Prob(pinf < rN) beyond which it is quite unlikely to estimate rN, knowing that the expected value is pinf . This threshold corresponds to the term q%, which represents a quantile of the normal distribution [8.21a], otherwise perfectly determined. By choosing the quantile to be situated at 2.5%, we find:
[8.22a] ![]()
pinf is, in this case, the estimate of the lower bound of the correlation coefficient, which is determined from the![]() empirical observation carried out from a sample of size N, with a probability of 97.5%.
empirical observation carried out from a sample of size N, with a probability of 97.5%.
To find the upper bound, the reasoning is perfectly similar and the symmetry of the normal distribution enables us to reach the following conclusion:
[8.22b] ![]()
We can thus deduce that the [pinf,psup] confidence interval at 95% for the true value of the correlation coefficient is given by:
[8.23] ![]()
By replacing the standard deviations with their expressions given in [8.20a], we obtain:
[8.24] 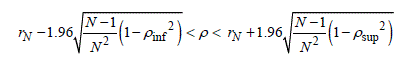
Assuming N is high enough, the sought after [pinf, psup] interval tends to decrease, and two new approximations can be made:
[8.25a] ![]()
[8.25b] ![]()
We thus obtain a final approximate expression of the uncertainty of estimation of the auto correlation function, mainly as a function of the sample size N whose moment of the first order correlation function is p:
[8.26] 
Although valid for correlation values p lower than 0.5, this confidence interval gives a higher uncertainty margin for strong correlation values. It may therefore also be applied in such cases.
Table 8.4 gives a few examples of the confidence interval for a few values of the pair (p,N) as calculated from [8.26].
Table 8.1. A few values of the confidence interval for the estimation of correlation coefficient p calculated from [8.26] for several known values of p and of the sample size N

It is thus quite possible in principle to reduce the confidence interval by increasing the size of the sample. However, if we study the rotation of a mode stirrer, this increase automatically leads to an increasing correlation between measurements. Reducing the confidence interval can require several successive evaluations of the correlation estimate, in different positions of the field probe for example.
We empirically show that this method enables us indeed to converge on confidence intervals which are determined by N = MP, where M is the number of stirrer positions, and P is the number of field probe positions. From a theoretical point of view, we then introduce a modification of the object of study, i.e. of the probability space, since randomness comes at the same time from the stirrer position and from the receiving position. However, because of the limited number of P positions, this is the correlation feature of the measurements carried out during the stirrer rotation which is estimated. This uncertainty estimate of the correlation function has been established under the assumption of the law of large numbers of realizations.
8.3.6. Residual correlation and impact on the reproducibility of the measurement sin reverberation chambers
We illustrate here with a measurement result the method proposed in the previous section. The reverberation chamber used for these measurements is identical to that of section 8.2. The frequency range under investigation is located between 600 MHz and 1,300 MHz. The stirrer, made up of several metal blades in rotation on a vertical axis located at one end of the chamber, is operated by a step-by-step motor. The complete rotation is carried out by a step of 1.2° and leads to the acquisition of an ordered series of 300 electric field measurements in one arbitrary location of the field probe in the working volume. The elementary rotation angle here is voluntarily small.
To obtain a relatively restricted uncertainty, five measurements of the same type are carried out in five different and arbitrary positions of the field probe. This is thus a succession of 5 x 300 measurements (N = 1,500), which will enable us to refine the correlation estimate. The estimate results of the auto correlation coefficient usually calculated according to [8.14] appear in Figure 8.5.
Observation of the correlation curve as a function of the frequency clearly shows that beyond 1,200 MHz, the 300 positions of the stirrer have a linear correlation which tends to become low. This curve has a mainly monotonous shape. The moving by 1.2° of the mode stirrer tends to alter – with increasing strength – the field distribution, while the frequency increases. The relatively strong correlation recorded at 600 MHz, indicates that the chosen rotation step is insufficient. At this frequency, the stirrer does not enable us to carry out the implementation of such a large number of independent observations.
Figure 8.5. Empirical determination of the auto correlation coefficient out of 1,500 measurements collected during a complete rotation of the stirrer and for several working frequencies symbolized by gray dots

This correlation implies a decrease in the number of independent realizations. In other words, the sample is far to be entirely random. When the correlation is null,the maximum possible number of independent implementations reaches 300. The maximum term is important here, since nothing authorizes us to say that all these measurements are independent. Independence involves non-correlation, but the reciprocal of this proposition is wrong. However, when the correlation is non-null,this results in the systematic decrease in the number of independent measurements. This decrease is more significant when this correlation is high.
It is possible to quantify this diminution by resorting to the calculation of the effective sample size. This is a question of seeking an equivalent sample of data Z(z1, z2,…, zNeq ) , of size Neq, whose statistical properties will be identical to the original sample X (x1, x2,…, xN ) . This theoretical sample follows the underlying distribution previously identified with the help of a goodness-of-fit test, according to the method presented in section 8.2 of this chapter. The estimate of the mean of this theoretical sample must follow the same behavior, which can be expressed in the form of the equality of the standard deviation to the mean ratio of the collected sample X with the standard deviation to the mean ratio of the theoretical sample Z:
[8.27] 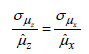
In this equation, μz and μx respectively designate the moment of the samples Z and X. ![]() respectively are the standard deviation of the estimate of this mean, linked to the central limit theorem. Thus, for the theoretical sample of Neqsize, we find quite naturally for the term located on the left of the equality [8.27]:
respectively are the standard deviation of the estimate of this mean, linked to the central limit theorem. Thus, for the theoretical sample of Neqsize, we find quite naturally for the term located on the left of the equality [8.27]:
[8.28] 
The term located on the right of this equality is much more difficult to determine.We will not give the development of this calculation here, focusing only at introducing the main steps of the reasoning. The complete details of this demonstration are notably given in [LEM 08a, LEM 08b]. To evaluate the behavior of ![]() , it is necessary to resort to an auto regressive model, which enables us to more precisely link the xi realization to the previous realizations. In the case of mechanical stirring in a reverberation chamber, those realizations correspond to the consecutive angular positions of the stirrer. The order of the auto regressive model is equal to the number of the previous correlated realizations of the model. An auto regressive model of the first order is sufficient to describe the behavior of a correlated series, for which the first order auto correlation coefficient is lower or of about 0.5. We can then show that the equality on the right side of equation [8.27] is given by:
, it is necessary to resort to an auto regressive model, which enables us to more precisely link the xi realization to the previous realizations. In the case of mechanical stirring in a reverberation chamber, those realizations correspond to the consecutive angular positions of the stirrer. The order of the auto regressive model is equal to the number of the previous correlated realizations of the model. An auto regressive model of the first order is sufficient to describe the behavior of a correlated series, for which the first order auto correlation coefficient is lower or of about 0.5. We can then show that the equality on the right side of equation [8.27] is given by:
[8.29] 
By replacing [8.27] with expressions [8.28] and [8.29], we reach the expression of Neq, as a function of N and of the estimate of the auto correlation function[LEM 08b]:
[8.30] 
In this expression the ![]() estimates have been replaced with the corresponding expected values of the underlying probability density function.
estimates have been replaced with the corresponding expected values of the underlying probability density function.
However, the corresponding parameters for the initially measured series X(x1, x2,…, xN ) must be estimated from this sample. We can admit that these estimates are close to the theoretical parameters, notably if N is sufficiently high.With this assumption, an approximated evaluation of [8.30] is established and it has a very simple form:
[8.31] 
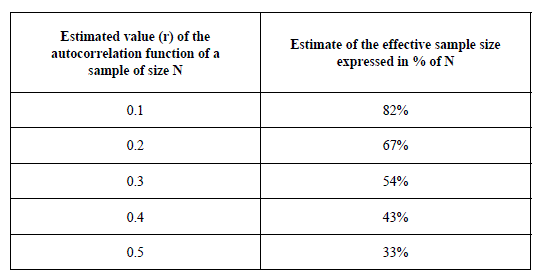
From this approximated formula, it is possible to estimate the impact of a linear correlation, even a residual one, on a series of measurement. Table 8.5 indicates the actual size in percentage of the initial sample size, for a few estimate values of the correlation according to expression [8.31].
This table very clearly shows the limitation of the effective sample size induced by the correlation within the collected sample. Thus, an estimate of the first order correlation function of about 0.3 approximately induces a reduction of half of the sample thus collected. As already mentioned in this book, measurements in reverberation chambers relies on mean value statistics whose uncertainty is inversely proportional to the square root of the number of independent realizations. This number of independent realizations cannot be higher than the effective sample size,such as determined according to [8.31]. Let us note that this result has been illustrated through experiments [LEM 08b].
Table 8.5. Estimate of the effective size of the sample in proportion to its initial size N expressed as a function of the estimated value of its first order auto correlation function
8.4. Quantization of the scattered and coherent fields in a reverberation chamber
In the following, we take a look at another imperfection of reverberation chambers and at its characterization: the non-stirred component of the electromagnetic field captured by a receiving probe or antenna. On the contrary, this non-stirred component can be voluntarily reinforced in order to create the Rice statistics, which are used very frequently in the context of modeling a propagationchannel.
8.4.1. Coherent residual field in a reverberation chamber and the Rice statistics
We have mentioned in section 8.2 the use of high power statistical tests, in order to detect the even small departure from the assumption of an ideal random field.This non-ideal statistics can be linked to the slightly non-uniform distribution of the incidence angles and of the field polarization.
To these considerations is also added the fact that the model of the ideal random field proposed by Hill, neglects any direct coupling phenomenon between the transmission antenna and the receiving antenna. In other words, this amounts to considering that the coupling between the antennas does not include any coherent component, i.e. whose amplitude and phase is predictable and do not vary while stirring the chamber. The mode stirrer used is then perfectly efficient, since its rotation makes the set of the waves collected by the receiving antenna appear as incoherently combined.
In reality, the experiment shows that there is, at the reception level, a fraction of coherent energy which is unaltered by the mode stirrer rotation. Thus, in order to optimize the efficiency of the mode stirring, it is interesting to seek configurations enabling us to reduce this fraction of coherent energy as much as possible. The standards recommend choosing antenna positions minimizing the direct coupling between antennas, without specifying however the methods enabling us to control the efficiency of the procedure.
For this, let us designate by S(f,θ) the complex amplitude of the sine wave generated in the chamber in steady state as a function of the frequency variable f and of the position variable θ of the mode stirrer. This function can be represented in the following form:
[8.32] ![]()
This is an expression in which Sc(f) represents the coherent fraction of the wave and Sd(f,θ) represents the scattered component which results from the mechanical stirring. In reality, the previous functions can have the complex forms expressed as follows:
[8.33] ![]()
[8.34] ![]()
where sc(f) and ϕc are the amplitude and phase of the coherent signal, both independent from the action of the stirrer. sdr(f,θ) and sdi(f,θ) represent the real and imaginary component of the scattered wave.
Let us specify that as a function of the angular variable θ, the real and imaginary part of the scattered wave captured by the receiver, which for example collect an electric field component, follow a normal distribution centered according to the hypothesis of an ideal random field. Consequently, in the absence of a coherent signal, the absolute amplitude of S(f,θ) = Sd(f,θ) would follow a Rayleigh process.
However, the presence of the coherent wave has the consequence of modifying the moment of the initial normal distribution of each of the real and imaginary components of S(f,θ).
Finally, the total S(f) = X(f) + jY(f) signal is the additive combination of two non-centered normal distribution, such as:
[8.35] 
where σd is the standard deviation of the scattered wave, generated in the chamber.
We can show that the random variable defined by ![]() follows a Rice distribution of (Sc(f),σd(f)) parameters. The f (z) probability density function of
the Rice distribution of (v,σ) parameters is recalled below:
follows a Rice distribution of (Sc(f),σd(f)) parameters. The f (z) probability density function of
the Rice distribution of (v,σ) parameters is recalled below:
[8.36] 
The I0 function represents the modified Bessel function of the first type and of 0order, which is given by the following integral form:
[8.37] 
Very often, notably in the context of the channel characterization or of the definition of a propagation channel model, we refer to the Rice K factor, recounting the existing ratio of the coherent and scattered power at the level of the receiver. The power carried by the coherent wave is given by:
[8.38] 
whereas the power carried by the scattered wave is given by:
[8.39] ![]()
We deduce from it the K factor in logarithmic scale:
[8.40] 
8.4.2. Goodness-of-fit test of a Rice distribution in a reverberation chamber
In order to quantify the K factor previously expressed, it is necessary to have a tour disposal a method of testing the hypothesis that a Rice distribution may fit a sample of the random variable |S(f)| = ![]() .
.
As we a priori should have at our disposal measurements of complex amplitudes, it is suitable to use a vector network analyzer to perform the measurement of the complex transfer function between two ports, one of them being connected to a transmitting antenna and the other one to a receiving antenna. The studied signal will thus be the S21 transfer function, whose behavior is comparable to the S(f,θ) signal of expression [8.32]. As the rectangular projection of the electric field, the S21 parameter is homogeneous to a square root of power and also follows a Rayleigh distribution in the absence of reception of a coherent wave.
The test for a Rice distribution will be indirectly done by carrying out a goodness-of-fit test for the normal distribution, and for both the real component and for the imaginary component of the S21 parameter.
The estimates of the first and second moments of a Norm(μr,σr) distribution(having the maximum likelihood) for the real component of the transfer function![]() are:
are:
[8.41] 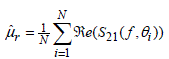
[8.42] 
Similarly, we estimate the parameters of the normal distribution Norm(μi,σi)for the parameters of the imaginary component of the transfer function ![]() .
.
The goodness-of-fit test for the normal distributions is carried out for the two empirical distributions ![]() and
and ![]() . In the case of acceptance of the assumption, the modulus of the transmission parameter follows a Rice distribution,whose estimators will be given by:
. In the case of acceptance of the assumption, the modulus of the transmission parameter follows a Rice distribution,whose estimators will be given by:
[8.43] 
From there, we then directly estimate the K factor according to expression [8.40].
8.4.3. Example of evaluation of a Rice channel in a reverberation chamber
The test of a Rice distribution is carried out on a series of measurements in a reverberation chamber for a quite particular configuration of transmitting and receiving horn antennas. This situation is drawn in a diagram in Figure 8.6.
Figure 8.6. Measurement configuration of the S21 parameter between two horn antennas in the line of sight for a Rice channel test. The distance is adjusted at 1 m and then at 3 m
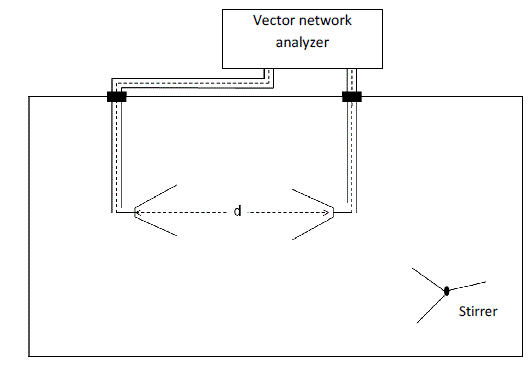
This configuration is not conventional in a reverberation chamber. Most of the time, we seek to avoid it, because it evidently favors the direct coupling between antennas. Moreover, horn antennas are rather directive antennas and an important fraction of the power may reach the receiving antenna, without the propagation environment offered by the reverberation chamber being involved. This recommendation to avoid direct coupling is constantly recommended in the standardization documents for EMC tests in reverberation chambers. It does not guarantee however the in existence of a coherent (non-stirred) signal [COR 00].Beyond the illustrative vocation of this measurement configuration, it has in reality two complementary interests.
On the one hand, the evaluation of the K coefficient of a Rice channel in these conditions can enable us to evaluate if this configuration is really detrimental from the point of view of the production of an ideal random field. From this point of view,the distance d separating the two antennas is an interesting variable, because we naturally expect that the fraction of coherent power received by the reception antenna decreases with the increase of this distance.
On the other hand, the implementation of a Rice channel is interesting in the context of emulating a realistic propagation channel for the test of multi-antenna communication systems [DEL 08, HOL 06, LIE 04, VAL 08]. This is a new prospect for reverberation chambers to which we will briefly return in the conclusion of this chapter.
The measurement is carried out in the following conditions. The working frequency is located between 3.45 GHz and 3.55 GHz, and the measurement is carried out for 1,001 frequencies per step of 100 kHz on the whole bandwidth. For each working frequency, we record the S21 parameter in amplitude and in phase, for30 different stirrer positions. It is then possible to evaluate a K(f) coefficient associated with each of these 1,001 frequencies, from a sample of 30 values of complex S21 parameters.
The method used to determine K(f) follows the method quoted in the previous section 8.4.2. The sample of 30 values of S21 is broken down into two samples gathering the real and imaginary components of S21. The goodness-of-fit test for the normal distribution is then carried out for these two samples, whose parameters would have been estimated previously according to [8.41] and [8.42]. These expressions are given for the real component.
In reality, all the tests show that the assumption of a normal law is perfectly acceptable, whatever the frequency in the considered bandwidth. This validates the postulate of a Rice distribution, whose parameters are estimated according to [8.43]. We easily deduce the K(f) parameter according to [8.40]. Figure 8.7 features the results of the numerous estimated K(f) values versus frequency for two arbitrarily chosen distances of 1 and 3 m separating the horn antennas.
Indeed, we notice that the observed K coefficient is of a different order of magnitude between the two measurement distances. It is clearly lower for a separation distance of 3 m between the two antennas. If we should evaluate the decrease of the coherent power similar to the decrease of the transmission balance between two antennas in free space, according to the Friis formula [FRI 46], the aforementioned would be proportional to the ratio of the square distances, i.e. almost about 10 dB in logarithmic unit. This represents the order of magnitude of the differences observed on the K factor quite well, which, according to Figure 8.7, is located around 10 dB for a distance of 1 m and at 0 dB for a distance of 3 m.
Figure 8.7. Evaluation results of the K(f) factor from a series of 30 measurements of S21 parameters, corresponding to 30 mode stirrer positions. This evaluation is produced for distances between antennas of 1 m and 3 m

Fluctuations of the K factor are very significant. In reality, we find two types of fluctuations. The very fast oscillations with the change of frequency are of about5 dB. They convey in reality the very strong statistical uncertainty of the evaluation,concerning in practice only a very limited (30) sample of measurements. We also distinguish a slower fluctuation of a smaller amplitude, which is probably linked to the evolution of the composite quality factor of the set of propagation modes successively excited at the different frequencies. If the coherent energy comes from wave interference, may be due to specular reflections on chamber walls, the latter can also contribute to the fluctuation of the K factor as a function of the frequency.The higher the distance, the more likely it may contribute to these fluctuations.
Fluctuation of the statistics of K can be reduced in several ways. The size of the sample can naturally be increased via the increase of a large number of stirrer positions.
We can also consider that the variations of K are slow as a function of the frequency and we can formulate the assumption that K remains constant in a reasonably chosen frequency band width. The choice of an interval of 10 MHz is adapted here, as shown by Figure 8.8. It then leads to the production of a mean of100 estimates of K.
Figure 8.8. Evaluation results of the K(f) factor from a series of 30 measurements of S21 coefficients corresponding to the 30 positions of the mode stirrer. Estimate in sliding average of K(f) on a set of 100 consecutive frequencies

The mean estimate curves are carried out in moving average on 100 estimates carried out on consecutive frequencies. The observation of the mean estimate curves shows that the residual fluctuations are relatively low and that it can be reasonable to consider K as almost constant on the entire considered frequency band.
8.5. Discussion
We have mentioned in this chapter a few lines about recent studies of reverberation chambers. Some are about the fine understanding of its functioning or else on the statistical analysis of the observed measurement series, but many other lines of study could have been tackled in this book.
Electromagnetic reverberation chambers have been, for example, the subject of the first experiments of time reversal of electromagnetic signals [LER 06]. Some studies have also shown its possible use for different potential applications in the domain of radio-frequencies. These applications concern for example the measurements of antenna efficiency, of diversity gain in a Rayleigh channel, of sensibility analysis of receivers, etc.
Recently, a new line of research has appeared, in the form of precursory works,for which we plan to artificially recreate propagation channels, which are controlled and perfectly reproducible for the test of multi-antenna terminals. The first investigations on this question show that to the cost of some adaptations, it is quite easy to reproduce some characteristic parameters of propagation channels, which are used as a reference for the development of standardized communication systems.
However, many questions remain to be studied and new developments will probably see the light.
There are also other domains within which reverberation chambers still have some mysteries. The functioning in transient regime of these chambers is a crucial matter, notably for understanding the nature of the immunity test in reverberation chambers, especially in pulsed regime.
The quest for an almost deterministic model, or on the contrary, of the specific statistical nature of the reverberation chambers potentially enables us to detect or evidence some properties. They may help to either confirm some experimental results or suggest other applications of reverberation chambers. We can also imagine that a reliable model, whatever its nature, could help for the optimization of these chambers in the future.
Studies seeking to decrease the lowest operating frequency of the chambers without growth of their volume also seem interesting for the users and providers of such testing systems.
Finally, recent research studies (and the upcoming studies) have been carried out throughout the world by an increasing number of teams during the last decade. Th islets us imagine new potential contributions to knowledge and certainly a wider range of applications.
This introductory book on the complex subject of reverberation chambers was limited to the basic physical and statistical concepts, for obvious didactic reasons.
Nevertheless, as shown by this last chapter, in-depth analysis of the phenomena encountered in these chambers inevitably leads to the use of very sophisticated theoretical developments, that the reader can find in many theses, articles and scientific reports, which are produced at a national and international level. In the near future this context will stimulate the writing of other books, which will offer a more specialized look at the physics and the applications of these chambers, but it will also stimulate a likely opening towards new theoretical concepts.
8.6. Bibliography
[ARN 02] ARNAUT L., “Compound exponential distributions for under-moded reverberation chambers”, IEEE Transactions on Electromagnetic Compatibility, vol. 44, no. 3, p. 442-457, August 2002.
[BUN 02] Bunting C. “Statistical characterization and the simulation of reverberation chamber using finite element techniques”, IEEE Transactions on Electromagnetic Compatibility, vol. 44, no. 1, p. 214-221, January 2002.
[COR 00] CORONA P., FERRARA G., MIGLIACCIO M., “Reverberating chamber electromagnetic field in presence of an unstirred component”, IEEE Transactions on Electromagnetic Compatibility, vol. 42, no. 2, p. 111-115, May 2000.
[DEL 08] DELANGRE O., Car actérisation et modélisation du canal radio en chambreréverbérante, Thesis, Free University of Brussels and Sciences and Technical University of Lille, 2008.
[DIO 07] DIOUF F., PALADIAN F., FOGLI M., CHAUVIERE C., BONNET P., “Emission in reverberation chamber: numerical evaluation of the total power radiated by a wire with a stochastic collocation method”, 18th International Zurich Symposium on EMC, p. 99-102, Munich, September 2007.
[DIO 08] DIOUF F., Application de méthodes probabilistes à l’analyse des couplages encompatibilité électromagnétique et contribution à la sûreté de fonctionnement dessystèmes électroniques, Thesis, Clermont II University, 2008.
[EVA 89] EVANS J.W., JOHNSON R.A., GREEN D.W., Two-and-three-parameter Weibull goodness-of-fit tests, Forest Products Laboratory, Forest Service, United States Department of Agriculture, research paper FPL-RP-493, Nov. 1989 [FIA 05] Fiachetti C., Modèles du champ électromagnétique aléatoire pour le calcul ducouplage sur un équipement électronique en chambre réverbérante à brassage de modes etvalidation expérimentale, Thesis, Limoges University, November 2002.
[FRI 46] FRIIS H.T., “A note on a simple transmission formula”, Proceedings of the I.R.E.and Waves and Electrons, p. 254-256, May 1946.
[IEC 02] International Electrotechnical Commission, IEC 61000-4-3, Testing and Measurement Techniques – Radiated, Radio-Frequency, Electromagnetic Field Immunity Test, Edition 2.1, Electromagnetic Compatibility (EMC), part 4-3, 2002.
[JOH 94] JONHSON N.L., KOTZ S., BALAKRISHNAN N., Continuous Uni variate Distributions,2nd edition, John Wiley & Sons, Oxford, 1994.
[HOE 01] HOEPPE F., Analyse du comportement électromagnétique des chambresréverbérantes à brassage de modes par l’utilisation de simulations numériques, Thesis,Lille University, 2001.
[HOL 06] HOLLOWAY C.L., HILL D.A., LADBURY J.M., WILSON P.F., KOEPKE G., CODER J.,“On the use of reverberation chambers to simulate a Rician radio environment for the testing of wireless devices”, IEEE Transactions on Antennas and Propagation, vol. 54, no. 11, p. 3167-3177, November 2006.
[KRA 05] KRAUTHAUSER H.G., WINZERLING T., NITSCH J., EULIG N., ENDERS A., “Statistical interpretation of auto correlation coefficients for fields in mode-stirred chambers”, IEEE International Symposium on EMC, vol. 2, p. 550-555, Chicago, August 2005.
[LAL 06] LALLECHERE S., Modélisations numériques temporelles des chambres réverbérantesen compatibilité électromagnétique. Contribution au schémas volumes finis, Thesis,Clermont II University, December 2006.
[LEM 07] LEMOINE C., BESNIER P., DRISSI M., “Investigations of reverberation chamber measurements through high-power goodness-of-fit tests”, IEEE Transactions on Electromagnetic Compatibility, vol. 49, no. 4, p. 745-755, November 2007.
[LEM 08a] LEMOINE C., Contribution à l’analyse statistique des mesures en chambreréverbérante à brassage de modes. Applications à la détermination de l’efficacité debrassage et de l’incertitude de mesure dans un contexte CEM et radiofréquence, Thesis,INSA of Rennes, July 2008.
[LEM 08b] LEMOINE C., BESNIER P., DRISSI M., “Estimating the effective sample size to select independent measurements in a reverberation chamber”, IEEE Transactions on Electromagnetic Compatibility, vol. 50, no. 2, p. 227-236, May 2008.
[LER 06] LEROSEY G., DE ROSNY J., TOURIN A., FINK M., “Time reversal of wide band microwaves”, Applied Physics Letters, vol. 15, p. 154101, 2006.
[LIE 04] LIENARD M., DEGAUQUE P., “Simulation of dual array multipath channels using mode-stirred reverberation chambers”, Electronic Letters, vol. 40, no. 10, p. 578-580,May 2004.
[LIL 67] LIlLIEFORS H.W., “Kolmogorov-Smirnov test for normality with mean and variance unknown”, Journal of the American Statistical Association, vol. 62, p. 399-402, June 1967.
[LUN 00] LUNDEN O., BACKSTROM M., “Stirrer efficiency in FOA reverberation chambers.evaluation of correlation coefficients and Chi-squared tests”, IEEE International Symposium on EMC, vol. 1, p. 17-22, August 2000.
[MAS 51] MASSEY F.J., “The Kolmogorov-Smirnov test for goodness of fit”, Journal of the American Statistical Association, vol. 46, p. 68-78, 1951.
[ORJ 06] ORJUBIN G., RICHALOT E., MENGUE S., PICON O., “Statistical model of anundermoded reverberation chamber”, IEEE Transactions on Electromagnetic Compatibility, vol. 48, no. 1, p. 248-251, February 2006.
[PAP 02] PAPOULIS A., UnniKRISHNA PilLAI S., Probability, Random Variables and Stochastic Processes, 4th edition, McGraw-Hill, New York, 2002.
[PET 02] PETIT F., Modélisation et simulation d’une chambre réverbérante à brassage demodes à l’aide des différences finies dans le domaine temporel, Thesis, Marne-la-ValléeUniversity, 2002.
[PRI 09] PRIMIANI V., MOGLIE F., Pastore A., “Field penetration through a wire mesh screen excited by a reverberation chamber field: FDTD analysis and experiments”, IEEE Transactions on Electromagnetic Compatibility, vol. 51, no. 4, p. 883-891, November 2009.
[RTC 07] RTCA-DO-160, Radio Technical Commission for Aeronautics, Environmental Conditions and Test Procedures for Airborne Equipment, version F, 2007.
[STE 74] STEPHENS M.A., “EDF statistics for goodness of fit and some comparisons”,Journal of the American Statistical Association, vol. 69, no. 347, p. 730-737, September 1974.
[VAL 08] VALENZUELA-VALDES J.F., MARTINEZ-GONZALES A.M., SANCHEZ-HeRnANDEZ D.A., “Emulation of MIMO non-isotropic fading environments with reverberation chambers”, IEEE Antennas and Wireless Propagation Letters, vol. 7, p. 325-328, 2008.
[WEI 51] WEIBUlL W., “A statistical distribution function of wide applicability”, ASME Journal of Applied Mechanics, Transactions of the American Society of Mechanical Engineers, p. 293-297, September 1951.
