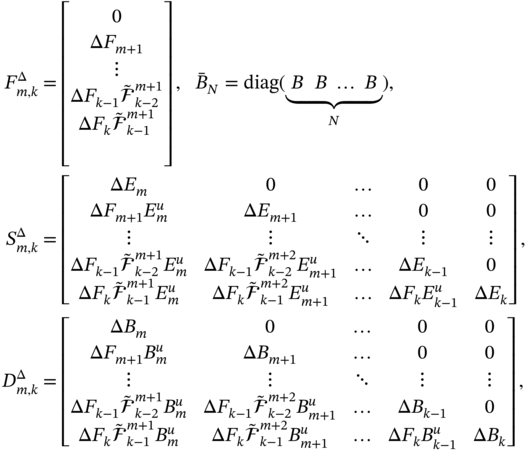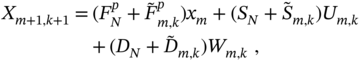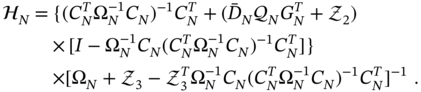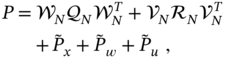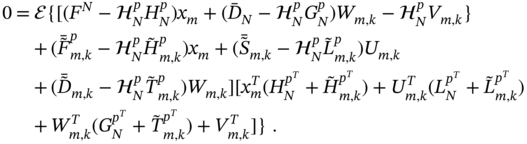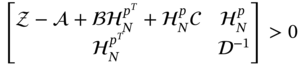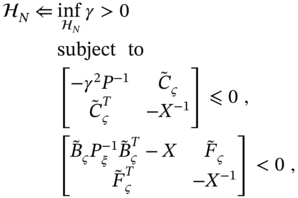9
Robust FIR State Estimation for Uncertain Systems
A statistical analysis, properly conducted, is a delicate dissection of uncertainties, a surgery of suppositions.
Michael J. Moroney [132], p. 3.
In physical systems, various uncertainties occur naturally and are usually impossible to deal with. An example is the sampling time that is commonly set constant but changes due to frequency drifts in low‐accuracy oscillators of timing clocks. To mitigate the effect of uncertainties, more process states can be involved that, however, can cause computational errors and latency. Therefore, robust estimators are required [79,161]. Most of works developing estimators for uncertain systems follow the approach proposed in [51], where the system and observation uncertainties are represented via a single strictly bounded unknown matrix and known real constant matrices. For uncertainties considered as multiplicative errors, the approach was developed in [56], and for uncertainties coupled with model matrices with scalar factors, some results were obtained in [180]. In early works on robust FIR filtering for uncertain systems [98,99], the problem was solved using recursive forms that is generally not the case. In the convolution‐based batch form, several solutions were originally found in [151,152] for some special cases.
Like in the case of disturbances, robust FIR estimators can be designed using different approaches by minimizing estimation errors for maximized uncertainties. Moreover, we will show that effects caused by uncertainties and disturbances can be accounted for as an unspecified impact. Accordingly, the idea behind the estimator robustness can be illustrated as shown in Fig. (9.1), which is supported by Fig. 8.3. Assume that an error factor 
exists from 
to 
and causes an unspecified impact 
(uncertainty, disturbance, etc.) to grow from point A to point C. Suppose that optimal tuning mitigates the effect by a factor 
and consider two extreme cases. By tuning an estimator to 
, we go from point A to point B. Then an increase in 
will cause an increase in tuning errors and in 
, and the estimation error can significantly grow. Now, we tune an estimator to 
and go from point C to D. Then a decrease in 
will cause an increase in tuning errors and a decrease in 
. Since both these effects compensate for each other, the estimate becomes robust.
In this chapter, we develop the theory of robust FIR state estimation for uncertain systems operating under disturbances with initial and measurement errors. In this regard, such estimators can be considered the most general, since they unify other robust FIR solutions in particular cases. However, further efforts need to be made to turn most of these estimators into practical algorithms.
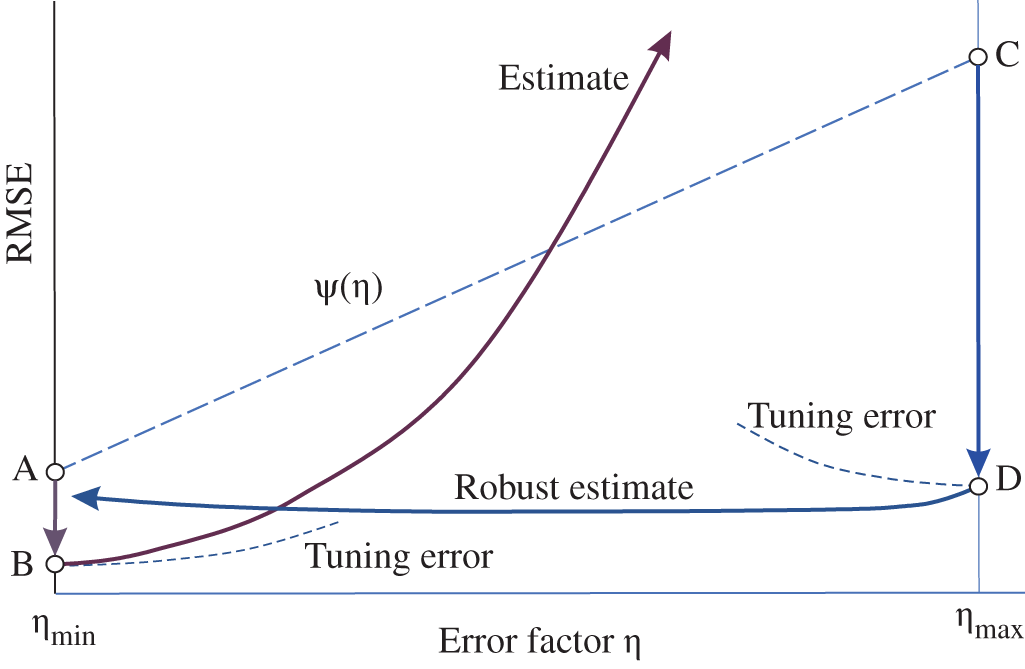
Figure 9.1 Errors caused by optimal tuning an estimator to 
and 
: tuning to 
makes the filter robust.
9.1 Extended Models for Uncertain Systems
Traditionally, we will develop robust FIR state estimators for uncertain systems using either a BE‐based model that is suitable for a posteriori FIR filtering or an FE‐based model that is suitable for FIR prediction and FIR predictive filtering. For clarity, we note once again that these solutions are generally inconvertible. Since the most elaborated methods, which guarantee robust performance, have been developed for uncertain LTI systems in the transform domain, we start with BE‐ and FE‐based state space models and their extensions on 
.
Backward Euler Method–Based Model
Consider an uncertain linear system and represent it in discrete‐time state‐space with the following equations,
where 
, 
, 
, 
, and 
. The time‐varying increments 
, 
, 
, 
, and 
represent bounded parameter uncertainties, 
is the disturbance, and 
is the measurement error. Hereinafter, we will use the superscript 
to denote uncertain matrices.
We assume that all errors in (9.1) and (9.2) are norm‐bounded, have zero mean, and can vary arbitrailry over time; so we cannot know their exact distributions and covariances. Note that the zero mean assumption matters, because otherwise a nonzero mean will cause regular bias errors and the model will not be considered correct.
To extend (9.1) and (9.2) to 
, we separate the regular and zero mean uncertain components and represent the model in standard form
where the zero mean uncertain vectors are given by
Then, similarly to (8.1), the model in (9.3) can be extended as
where matrices 
and 
are defined after (8.4) and the extended error vector 
and matrix 
are given by
We next extend the uncertain vector 
to 
as
where the uncertain block matrices are defined by
in which 
and 
hold for 
, and matrix 
of the uncertain product is specified with
By combining (9.7) with (9.9) and referring to the identity 
, where matrix 
is defined after (8.4), we rewrite model (9.7) as
where 
, 
, and 
. We now notice that, for systems without uncertainties, 
, 
, and 
bring (9.12) to the standard form (8.3).
The system current state 
can now be expressed in terms of the last row vector in (9.12) as
where 
, 
, and 
are the last row vectors in 
, 
, and 
, respectively.
We also extend the observation model (9.4) as
where matrices 
and 
are defined after (8.4), 
, and 
is the vector of uncertain observation errors, which has the following extension to 
,
for which the uncertain matrices are given by
, 
is specified after (9.10), and 
and 
are diagonal.
By combining (9.14) and (9.15), we finally represent the extended observation equation in the form
where the uncertain matrices are defined in terms of the matrices introduced previously as
It can now be shown that exact modeling with 
, 
, and 
makes (9.17) the standard model (8.4).
Thus, the BE‐based state‐space model in (9.1) and (9.2), extended to 
for organizing a posteriori FIR filtering of uncertain systems under bounded disturbances with initial and data errors, is given by (9.13) and (9.17).
Forward Euler Method–Based Model
Keeping the definitions of vectors and matrices introduced for (9.1) and (9.2), we now write the FE‐based state‐space model for uncertain systems as
By reorganizing the terms, we next represent this model in the standard form
where the uncertain vectors associated with the prediction are denoted by the superscript 
and are given by
Obviously, extensions of vectors (9.23) and (9.24) to 
can be provided similarly to the BE‐based model. Referring to (8.8), we first represent (9.23) on 
with respect to the prediction vector 
as
where 
, 
, and 
, 
, and 
are defined after (8.4). Similarly to (9.9), we also express the vector 
on 
as
where matrix 
is defined by
Combining (9.27) and (9.28), we finally obtain the extended state equation
where 
, 
, and 
, and notice that zero uncertainties make equation 9.30 equal to (8.8).
The predicted state 
can now be extracted from (9.30) to be
where 
is the last row vectors in 
and 
and 
are defined after (9.13).
Without any innovation, we extend the observation equation 9.24 to 
as
where 
, 
, and
Similarly, we extend the vector 
as
where 
,
and matrices 
and 
are defined previously.
Finally, substituting (9.28) and (9.34) into (9.32) and reorganizing the terms, we obtain the extended observation equation
where the uncertain matrices are given by
and all other definitions can be found earlier. The last thing to notice is that without uncertainties, (9.35) becomes the standard equation (8.9).
Now that we have provided extended models for uncertain systems, we can start developing FIR filters and FIR predictors.
9.2 The a posteriori H2 FIR Filtering
Various types of a posteriori 
FIR filters (optimal, optimal unbiased, ML, and suboptimal) can be obtained for uncertain systems represented by the BE‐based model. Traditionally, we start with the a posteriori FIR filtering estimate defined using (9.17) as
where the uncertain matrices 
, 
, and 
are given by (9.18)–(9.20).
Under the assumption that all error factors, including the uncertainties, have zero mean, the unbiasedness condition 
applied to (9.13) and (9.39) gives two unbiasedness constraints,
We now write the estimation error 
as
and generalize with
where the regular error residual matrices 
, 
, and 
are given by (8.15)–(8.17), 
is the regular bias caused by the input signal and removed in optimal and optimal unbiased filters by the constraint (9.41), and the uncertain error residual matrices are defined as
By introducing the disturbance‐induced errors
and the uncertainty‐induced errors
and then neglecting regular errors by embedding the constraint (9.41), we represent the estimation error as the sum of the sub errors as
where the components are given by (9.47) and (9.48).
In the transform domain, we now have the structure shown in Fig. 9.2, where we recognize two types of errors caused by 1) disturbance and errors and 2) uncertainties, and the corresponding transfer functions:
is the 
‐to‐
transfer function (initial errors).
is the 
‐to‐
transfer function (disturbance).
is the 
‐to‐
transfer function (measurement errors).
is the 
‐to‐
transfer function (initial uncertainty).
is the 
‐to‐
transfer function (system uncertainty).
is the 
‐to‐
transfer function (input uncertainty).
Figure 9.2 Errors in the 
‐OFIR state estimator caused by uncertainties, disturbances, and errors in the 
‐domain.
Using the definitions of the specific errors and the transfer functions presented earlier and in Fig. 9.2, different types of FIR filters can be obtained for uncertain systems operating under disturbances, initial errors, and data errors. Next we start with the a posteriori 
‐OFIR filter.
9.2.1 
‐OFIR Filter
To obtain the a posteriori 
‐OFIR filter for uncertain systems, we will need the following lemma.
To obtain the a posteriori 
‐OFIR filter using lemma 9.1, we first note that the initial state error 
goes to 
unchanged and the 
‐to‐
transfer function is thus an identity matrix, 
. Using lemma 9.1, we then write the squared norms for the disturbances and errors as
The squared Frobenius norms associated with uncertain errors can be specified similarly. For the 
‐to‐
transfer function, we write the squared norm 
as
where the uncertain error matrices are defined by
Likewise, for the 
‐to‐
transfer function we write the squared norm 
as
where the uncertain error matrices are given by
Finally, for the 
‐to‐
transfer function we obtain the squared norm 
as
using the uncertain error matrices
Using the previous definitions, we can now represent the trace of the estimation error matrix 
associated with the estimation error (9.48) as
and determine the gain 
for the a posteriori 
‐OFIR filter by solving the following minimization problem
where the norms for uncertain errors are given by (9.53), (9.58), and (9.63).
Since the 
filtering problem is convex, we equivalently consider instead of (9.68) the equality
for which the trace 
can be written as
where 
.
By applying the derivative (9.69) to (9.70), neglecting the correlation between different error sources, and setting 
that gives 
, we finally obtain the gain for the a posteriori 
‐OFIR filter applied to uncertain systems operating under disturbances, initial errors, and data errors,
As can be seen, zero uncertain terms make (9.71) the gain (8.34) obtained for systems operating under disturbances, initial errors, and data errors. This means that the gain (9.71) is most general for LTI systems.
For the gain 
obtained by (9.71), we write the a posteriori 
‐OFIR filtering estimate as
and specify the estimation error matrix as
where the uncertain error matrices are defined by
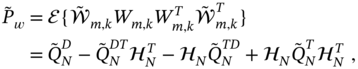
Any uncertainty in system modeling leads to an increase in estimation errors, which is obvious. In this regard, using the 
‐OFIR filter with a gain (9.71) gives a chance to minimize errors under the uncertainties. However, a good filter performance is not easy to reach. Efforts should be made to determine boundaries for all uncertainties and other error matrices (9.74)–(9.76). Otherwise, mistuning can cause the filter to generate large errors and lose the advantages of robust filtering.
Equivalence with OFIR Filter
Not only for theoretical reasons, but rather for practical utility, we will now show that the gain (9.71) of the a posteriori 
‐OFIR filter obtained for uncertain systems is equivalent to the OFIR filter gain valid in white Gaussian environments. Indeed, for white Gaussian noise the FIR filter optimality is guaranteed by the orthogonality condition 
that, if we use (9.17) and (9.43), can be rewritten as
Assuming all error sources are independent and uncorrelated zero mean white Gaussian processes and providing the averaging, we can easily transform (9.77) to (9.71). This provides further evidence that, according to Parseval's theorem, minimizing the error spectral energy in the transform domain is equivalent to minimizing the MSE in the time domain.
9.2.2 Bias‐Constrained 
‐OFIR Filter
A known drawback of optimal filters is that optimal performance cannot be guaranteed without setting correct initial values. This is especially critical for the 
‐OFIR and OFIR filters, which require initial values for each horizon 
. To remove the requirement of the initial state in the 
‐OFIR filter, its gain must be subject to unbiasedness constraints, and then the remaining errors can be analyzed as shown in Fig. 9.3.
Figure 9.3 Errors in the 
‐OUFIR state estimator caused by uncertainties, disturbances, and data errors in the 
‐domain.
Referring to the previous, we can now design the 
‐OUFIR filter for uncertain systems, minimizing the trace of the error matrix (9.73) subject to the constraint (9.40). As in the case of the OUFIR filter, the gain obtained in such a way is freed from the regular errors, and its error matrix depends only on uncertainties, disturbances, and data errors, as shown in Fig. 9.3. Next we give the corresponding derivation.
First, we use (9.74)–(9.76) and represent the error matrix (9.73) as
where the newly introduced uncertain matrices have the form
The Lagrangian cost function associated with (9.78) becomes
and we determine the gain 
by solving the minimization problem
The solution to (9.83) is available by solving two equations
and we notice that (9.85) is equivalent to the unbiasedness constraint (9.40).
The first equation 9.84 gives
Multiplying both sides of (9.86) from the left‐hand side by a nonzero 
and referring to the constraint (9.85), we obtain
and retrieve the Lagrange multiplier
Reconsidering (9.84), substituting (9.85) and (9.87), and performing some transformations, we obtain the gain for the 
‐OUFIR filter in the form
Note that for zero uncertain matrices 
and 
, the gain (9.88) becomes the gain (8.42) of the 
‐OUFIR filter, which is valid for systems affected by disturbances. The obvious advantage of (9.88) is that it does not require initial values and thus is more suitable to operate on 
.
Summarizing, we note that for 
determined by (9.88), the 
‐OUFIR filtering estimate 
and error matrix 
are obtained as, respectively,
where the error matrices 
, 
, and 
associated with system uncertainties are given by (9.74)–(9.76). It is worth noting that the uncertain component 
cannot be removed by embedding unbiasedness, since it represents zero mean uncertainty in the initial state. The same can be said about the uncertain matrix 
, which is caused by the zero mean input uncertainty.
9.3 H2 FIR Prediction
When an uncertain system operates under disturbances, initial errors, and measurement errors, then state feedback control can be organized using a 
‐OFIR predictor, which gives robust estimates if the error matrices are properly maximized. The prediction can be organized in two ways. The one‐step ahead predicted estimate can be obtained through the system matrix as 
or 
. Note that there is a well‐founded conclusion, drawn in [119] and corroborated in [171], that such an unbiased prediction can provide more accuracy than optimal prediction. Another way is to derive an optimal predictor that we will consider next.
Using the FE‐based model, we define the one‐step FIR prediction as
where the uncertain matrices 
, 
, and 
are given by (9.36)–(9.38).
The unbiasedness condition 
applied to (9.31) and (9.91) yields two unbiasedness constraints,
and the estimation error 
becomes
By embedding (9.93), we next generalize 
in the form
where the regular error residual matrices 
, 
, and 
are given by (8.60)–(8.62) and the uncertain error residual matrices can be taken from (9.94) as
Following Fig. 9.1, we now introduce the disturbance‐induced errors
and the uncertainty‐induced errors
and represent the estimation error as
It should now be noted that with the help of (9.101) we can develop different kinds of FIR predictors for uncertain systems operating under disturbances in the presence of initial and data errors.
9.3.1 Optimal 
FIR Predictor
Using lemma 9.1, it is a matter of similar transformations to show that the trace of the error matrix of the 
‐OFIR predictor is given by
where the squared weighted sub‐norms for the properly chosen weight 
are defined by
The first three squared norms in (9.102) are given by
The squared norm 
can be found using (9.100) and (9.96) to be
where the uncertain error matrices are defined by
The squared norm 
can be transformed to
by introducing the uncertain error matrices
Likewise, the squared norm 
can be represented with
using the uncertain error matrices
Based upon (9.102) and using the previously determined squared sub‐norms, we determine the gain for the 
‐OFIR predictor by solving the following minimization problem
where the uncertain norms are given by (9.107), (9.112), and (9.117). To find 
, we further substitute (9.122) equivalently with
and transform the trace 
to
where 
.
By applying the derivative (9.123) to (9.124), we obtain the gain for the 
‐OFIR predictor as
and notice that, by neglecting the uncertain terms, this gain becomes the gain (8.70) derived for systems operating under disturbances.
Finally, we end up with the batch 
‐OFIR prediction
where gain 
is given by (9.125), and write the error matrix as
where the uncertain error matrices are defined by
The batch form (9.126) gives an optimal prediction of the state of an uncertain system operating under disturbances, initial errors, and measurement errors. Because this algorithm operates with full block error matrices, it can provide better accuracy than the best available recursive Kalman‐like scheme relying on diagonal block error matrices. Next, we will show that the gain (9.125) of the 
‐OFIR predictor (9.126) generalizes the gain of the OFIR predictor for white Gaussian processes.
Equivalence with OFIR Predictor
By Parseval's theorem, the minimization of the error spectral energy in the transform domain is equivalent to the minimization of the MSE in the time domain. When all uncertainties, disturbances, and errors are white Gaussian and uncorrelated, then the orthogonality condition 
applied to (9.32) and (9.101) guarantees the FIR predictor optimality. Accordingly, we have
Providing averaging in (9.131) for mutually independent and uncorrelated error sources, we transform (9.131) into (9.124) and note that the 
‐OFIR predictor has the same structure as the OFIR predictor. The obvious difference between these solutions resides in the fact that the 
‐OFIR predictor does not impose restrictions on the error matrices, while the OFIR predictor requires them to be white Gaussian, that is, diagonal. Then it follows that the 
‐OFIR predictor is a more general estimator for LTI systems.
9.3.2 Bias‐Constrained 
‐OUFIR Predictor
Referring to the inherent disadvantage of optimal state estimation of uncertain systems, which is an initial state requirement, we note that the 
‐OFIR predictor may not be sufficiently accurate, especially for short 
, if the initial state is not set correctly. In 
‐OUFIR prediction, this issue is circumvented by embedding the unbiasedness constraint, and now we will extend this approach to the 
‐OUFIR predictor.
Considering the error matrix (9.127) of the 
‐OFIR predictor, we first remove the term containing 
using the unbiasedness constraint (9.92). Then we rewrite (9.127) as
where the matrices 
, 
, and 
are defined as
in terms of the uncertain matrices specified for the 
‐OFIR predictor.
We now write the Lagrangian cost function for (9.132),
and determine the gain 
by solving the minimization problem
The solution to (9.137) can be found by solving two equations
where the second equation 9.139 is equal to the constraint (9.92).
From the first equation 9.138 we find
We then multiply both sides of (9.140) from the left‐hand side with a nonzero 
and, using the constraint (9.92), obtain
From (9.141), we extract the Lagrange multiplier
Looking at (9.138) again, substituting (9.142), and providing some transformations, we finally obtain the gain for the 
‐OUFIR predictor as
As in the previous cases of state estimation of uncertain systems, we take notice that the zero uncertain matrices 
and 
make the gain (9.143) equal to the gain (8.70) of the 
‐OUFIR predictor, developed under disturbances and measurement errors. We also notice that the gain (9.143) does not require initial values and thus is more suitable for finite horizons.
Finally, the 
‐OUFIR prediction 
can be computed using (9.126), and the error matrix 
can be written by neglecting 
as, respectively,
where the uncertain error matrices 
, 
, and 
are defined by (9.128)–(9.130) and the gain 
is given by (9.143).
To summarize, it is worth noting that, as in the 
‐OUFIR filter case, efforts should be made to specify the uncertain matrices for (9.143). If these matrices are properly maximized, then prediction over 
can be robust and sufficiently accurate. Otherwise, errors can grow and become unacceptably large.
9.4 Suboptimal 
FIR Structures Using LMI
Design of hybrid state estimators with improved robustness requires suboptimal 
FIR algorithms using LMI. Since hybrid FIR structures are typically designed based on different types of 
estimators, the 
algorithm should have a similar structure using LMI. In what follows, we will consider such suboptimal FIR algorithms.
9.4.1 Suboptimal 
FIR Filter
To obtain the numerical gain 
for a suboptimal 
FIR filter using LMI, we refer to (9.73) and introduce an additional positive definite matrix 
such that
Substituting the error residual matrices taken from (8.15)–(8.17) and (9.74)–(9.76), we rewrite the inequality (9.146) as
and represent it with
where the introduced auxiliary matrices are given by
Using the Schur complement, we finally represent the inequality (9.147) with the following LMI
The gain 
for the suboptimal 
FIR filter can now be computed numerically by solving the following minimization problem
As in other similar cases, the best candidate for starting solving (9.153) is the UFIR filter gain 
. Provided that 
is found numerically, the suboptimal 
FIR filtering estimate can be computed as
and the error matrix 
can be computed by (9.73).
9.4.2 Bias‐Constrained Suboptimal 
FIR Filter
In a like manner, the gain for the bias‐constrained suboptimal 
FIR filter appears in LMI form, if we refer to (9.90) and introduce an auxiliary positive definite matrix 
such that
where the error residual matrices are given by (8.16), (8.17), and (9.74)–(9.76). Then we rewrite (9.155) as
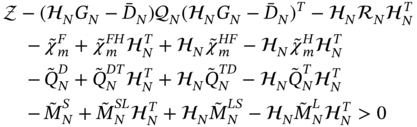
and transform to
using the following auxiliary matrices,
Using the Schur complement, we represent (9.156) in the LMI form as
and determine the gain for the bias‐constrained suboptimal 
FIR filter by solving numerically the following minimization problem
Traditionally, we start the minimization with 
. Provided that 
is numerically available from (9.162), the suboptimal 
FIR filtering estimate is computed by
and the error matrix 
is computed using (9.90). Note that the gain 
obtained by solving (9.162) is more robust due to the rejection of the initial state requirement.
9.4.3 Suboptimal 
FIR Predictor
To find the suboptimal gain for the 
FIR predictor using LMI, we introduce an auxiliary positive definite matrix 
to satisfy the inequality
We then use (8.60)–(8.62) and (9.128)–(9.130) and transform (9.164) to
where the uncertain matrices are the same as for the 
FIR predictor. We next represent this inequality as
where the introduced auxiliary matrices are the following
Using the Schur complement, we represent (9.165) in the LMI form
that allows finding numerically the gain for the 
FIR predictor by solving the following minimization problem
using 
as an initial try. The suboptimal 
FIR prediction can finally be computed by
and the error matrix 
by (9.127).
9.4.4 Bias‐Constrained Suboptimal 
FIR Predictor
As before, to remove the requirement of the initial state, the gain for the bias‐constrained suboptimal 
FIR predictor can be computed using LMI. To do this, we traditionally look at (9.145) and introduce a positive definite matrix 
such that
We then use the error residual matrices (8.61), (8.62), and (9.128)–(9.130) and transform (9.173) to
which we further generalize as
using the auxiliary matrices
Using the Schur complement, (9.174) can now be substituted by the LMI
and the gain for the bias‐constrained suboptimal 
FIR predictor can be numerically found by solving the minimization problem
if we start with 
. Finally, the bias‐constrained suboptimal 
prediction can be obtained as
and the error matrix 
can be computed using (9.145).
9.5 
FIR State Estimation for Uncertain Systems
To obtain various robust 
FIR state estimators for uncertain systems, we will start with the estimation errors of the FIR filter (9.49) and the FIR predictor (9.101) and will follow the lines previously developed to estimate the state under disturbances. Namely, using the induced norm 
defined by (8.90), we will find the gain for the 
FIR estimator corresponding to uncertain systems by numerically solving the familiar suboptimal problem
where the scalar factor 
, which indicates the part of the maximized uncertainty energy that goes to the output, should preferably be small. In what follows, we will develop an 
filter and an 
predictor for uncertain systems operating under disturbances, initial errors, and measurement errors.
9.5.1 The a posteriori
FIR Filter
Consider an uncertain system operating under a bounded zero mean disturbance 
and measurement error 
. Put 
and represent this system with the BE‐based state‐space model (9.1)–(9.2) as
where 
, 
, 
, and 
. Note that the uncertain increments 
, 
, 
, and 
represent time‐varying bounded parameters specified after (9.2).
We rewrite model (9.183) and (9.184) in the form of (9.3) and (9.4) as
where the zero mean uncertain error vectors 
and 
are defined by
to play the role of zero mean errors in the model in (9.185) and (9.186).
Following (9.13) and (9.17), we next extend the model in (9.185) and (9.186) to 
as
where 
and 
are the last row vectors in the uncertain matrices 
and 
, respectively. Note that the matrix 
is given by (9.8), 
and 
by (9.10), 
by (9.18) using (9.16), and 
by (9.20) using (9.16).
The 
FIR filter can now be derived for uncertain systems if we write the estimation error (9.43) for 
as
where the error residual matrices are given by (8.15)–(8.17), (9.44), and (9.46),
and the vectors 
and 
can be written using lemma 8.1 as
where the sparse matrices 
and 
are defined by (8.19).
Using (9.197), (9.198), and the augmented vectors 
, where 
, and 
, we write the uncertainty‐to‐error state space model in the standard form
where the sparse matrices 
and 
are given by (8.109) as
and all terms containing gain 
are collected in the matrix 
,
which is a very important algorithmic property of this model. Indeed, there is only one matrix 
, whose components are functions of 
, which makes the model in (9.199) and (9.200) computationally efficient.
Using (9.199) and (9.200), we can now apply the BRL lemma 8.2 and develop an a posteriori 
FIR filter using LMI for uncertain systems operating under disturbances and measurement errors. Traditionally, we will look at the solutions taking notice of the necessity to have a numerical gain 
such that 
satisfying (9.182) reaches a minimum for maximized uncertainties. The following options are available:
- Apply lemma 8.2 to (9.199) and (9.200) and observe that
, 
, and 
. For some symmetric matrix 
, find the gain 
, which is a variable of the matrix 
(9.202), by minimizing 
to satisfy the following LMI
- Consider (8.101), assign
, and solve for 
the following LMI problem by minimizing 
,
(9.204)
- Solve for
the following DARE by minimizing 
,
The robust a posteriori 
FIR filtering estimate and the error matrix can now be suboptimally computed for maximized zero mean uncertainties, disturbances, data errors, and initial errors by, respectively,
using the gain 
, obtained by one of the previous algorithmic options, and the error residual matrices in (9.192)–(9.196). It is worth noting that, although all of the previous algorithmic options are feasible, the LMI form (9.203) is the most elaborate.
9.5.2 
FIR Predictor
Robust prediction based on the 
FIR approach can be organized for uncertain systems in the same way as for systems operating under disturbances and measurement errors. To find a suboptimal gain for the 
FIR predictor, we traditionally use the FE‐based model in (9.21) and (9.22) with 
,
and represent it by reorganizing the terms as
where the uncertain error vectors are given by
We extend the model in (9.210) and (9.211) to 
as
where the matrix 
is the last row vector in matrix 
defined using (9.8) and (9.29), 
is specified after (9.13), 
by (9.36), and 
by (9.38). We next take the regular error residual matrices 
, 
, and 
from (8.60)–(8.62) and rewrite the estimation error (9.95) as
where the remaining uncertain error residual matrices are given by
Using lemma 8.1, we also represent 
and 
as (8.105) and (8.106),
where matrices 
and 
are defined by (8.19).
Now, we assign vectors 
, where 
, and 
, follow the lines developed after (9.184), and obtain the uncertainty‐to‐error state‐space model
in which the sparse matrices 
and 
are given after (8.108) and matrices 
and 
are defined by (8.133) as
where the matrix 
is given by
This model does not reveal any new features, and we simply note that, as in 
FIR filtering, the error residual matrices are collected here in the modified observation matrix 
(9.226), which is thus completely responsible for the performance of the 
FIR predictor.
We can now apply the BRL lemma 8.3 to (9.222) and (9.223) and develop a suboptimal 
FIR predictor by satisfying the performance criterion (9.182). By avoiding repeating the details of the steps above, we simply list the three main options here:
- Apply lemma 8.3 to (9.224) and (9.225) and note that
and 
. For some symmetric matrix 
, solve for 
the LMI problem
starting with 
. - Refer to (8.136) and solve the following LMI problem
(9.228)starting with the same initial
as in (9.227). - Solve the DARE
subject to
.
The 
FIR predictor can finally be summarized with the following estimate and error matrix, respectively,
where all the error residual matrices are functions of the gain 
, which must be computed numerically by solving the LMI problem using one of three options (9.227)–(9.229).
9.6 Hybrid 
FIR Structures
In an effort to achieve the highest robustness in estimating uncertain systems, the design of hybrid structures that combine the properties of different estimators is considered a top priority. As we will show, such structures can be created taking into account disturbances, initial errors, and data errors.
The a posteriori
FIR Filter
A hybrid LMI‐based algorithm to numerically compute the suboptimal gain 
for the a posteriori 
FIR filter can be developed by solving the following minimization problem subject to constraints (9.152) and (9.203),
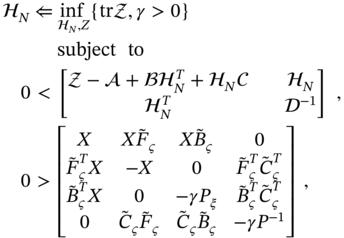
for which all matrices can be taken from the definitions given for (9.152) and (9.203). Initialization must be started with some symmetric matrix 
and 
. Since both constraints serve to minimize 
, such a hybrid FIR structure is considered more robust than either of the 
and 
FIR filters.
Suboptimal 
FIR Predictor
Similarly to the 
filter, a hybrid LMI‐based algorithm for numerically computing the suboptimal gain 
for the 
FIR predictor can be developed by solving the following minimization problem subject to constraints (9.170) and (9.227),
for which all matrices can be taken from the definitions given for (9.170) and (9.227). Initialization of the minimization procedure must be started using some symmetric matrix 
and 
. Like the hybrid 
FIR filter, the hybrid 
FIR predictor is also considered more robust than the 
FIR predictor and the 
FIR predictor.
9.7 Generalized 
FIR Structures for Uncertain Systems
In Chapter, we developed the robust generalized 
approach for FIR state estimators operating under disturbances. Originally formulated in [213] and discussed in detail in [188], the approach suggests minimizing the peak error for the maximized disturbance energy in the energy‐to‐peak or 
‐to‐
algorithms using LMI. We also showed that using the energy‐to‐peak lemma the gain for the corresponding FIR state estimator can be obtained by solving the following optimization problem
Now it is worth noting that if we consider 
in a broader sense, then the problem (9.234) can be extended to uncertain systems operating under disturbances, initial errors, and measurement errors. Following the same reasoning as for systems affected by disturbances, next we will use the FE‐ and BE‐based state space models modified for uncertain systems and develop robust algorithms using LMI to numerically compute the gains for 
‐to‐
FIR filter and predictor.
9.7.1 The a posteriori
‐to‐
FIR Filter
Unlike the standard 
approach, the robust generalized 
approach does not require the matrix 
to be necessarily zero. Therefore, we modify the BE‐based state‐space model (8.143) and (8.144) for the system 
and write
where the uncertain matrices 
, 
, 
, and 
are defined after (9.1) and (9.2). We assume that the disturbance 
and the data error 
are norm‐bounded, 
and 
, reorganize the terms, and represent the model in (9.235) and (9.236) in the standard LTI form
where the newly introduced zero mean uncertain errors are given by
We next extend the model in (9.237) and (9.238) to 
as
where the matrices 
and 
are the last row vectors in the uncertain matrices 
and 
, respectively. Matrix 
is given by (9.8), 
and 
by (9.10), 
by (9.18) using (9.16), and 
by (9.20) using (9.16).
The estimation error (9.43) can now be rewritten for 
as
where the error residual matrices are given by (8.15)–(8.17), (9.44), and (9.46),
and the vectors 
and 
can be represented using lemma 8.1 by (9.197) and (9.198), respectively.
Using (9.243), (9.197), (9.198), and the augmented vectors 
, where 
, and 
, we obtain the uncertainty‐to‐error state‐space model in the standard form
where the constant sparse matrices 
and 
are given by (9.201) and the 
‐varying matrix 
is defined by (9.202) as
Using the model (9.244) and (9.245) and the energy‐to‐peak lemma 8.4, we can finally design of a numerical algorithm using LMI for computing the suboptimal gain for the a posteriori 
‐to‐
FIR filter for uncertain systems operating under disturbances, initial errors, and measurement errors. Taking into account 
in (9.245), the algorithm becomes as follows.
Solve for 
the following minimization problem,
by initializing the minimization with 
. Provided that 
is numerically available, the a posteriori 
‐to‐
FIR filtering estimate and the error matrix can be computed by, respectively,
where the error residual matrices are introduced after (9.243). What should not be left behind is that the algorithm (9.247) can also be included in hybrid structures to improve robustness.
9.7.2 
‐to‐
FIR Predictor
Similar to the filtering counterpart, we can develop the 
‐to‐
FIR predictor for uncertain systems. To make it possible to avoid the details, we start with the FE‐based state‐space model (9.21) and (9.22) and rewrite it as
where 
is a bounded disturbance, 
. By reorganizing the terms, we represent (9.250) and (9.251) as
where the uncertain zero mean vectors are defined by
Using the same from as before, we extend the model (9.252) and (9.253) to 
as
where 
is the last row vectors in the uncertain matrix 
and 
is defined after (9.13). The uncertain matrices 
and 
are given by (9.36) and (9.38), respectively.
We now write the prediction error as
for which the regular and uncertain error residual matrices 
, 
, 
, 
, and 
are listed here
and the matrices 
and 
are given by (9.197) and (9.198),
where the sparse matrices 
and 
are defined by (8.19).
Combining the augmented vectors 
, where 
, and 
, we come up with the uncertainty‐to‐error state model
where the matrices 
and 
are given by (8.109).
Referring to (9.259)–(9.263), we next represent the prediction error (8.158) in the compact form
where the matrix 
is defined by
By combining 
taken from (9.265) and 
taken from (9.264), we finally obtain the estimation error as
At this point, we replace in (9.264) the time index 
with 
, accept 
that is not very critical, and arrive at the disturbance‐to‐error state‐space model in the desired form of (8.117) and (8.118),
where the sparse matrices 
and 
are given by (8.109) and the matrices 
and 
are defined by
Now, the 
‐to‐
FIR predictor can be developed for uncertain systems operating under disturbances, initial errors, and measurement errors if we apply lemma 8.4 to the model in (9.268) and (9.269). This results in the following numerical procedure to numerically compute the suboptimal gain 
.
For some positive define matrix 
, solve the minimization problem
where matrices 
and 
are specified by (9.270). Initialize the minimization with 
. Provided that 
is available from (9.271), the 
‐to‐
FIR prediction appears as 
with the error matrix
where the error residual matrices defined by (9.259)–(9.263) are functions of 
computed numerically by solving the minimization problem (9.271). Finally note that this algorithm can also be included in robust hybrid FIR predictive algorithms.
9.8 Robust 
FIR Structures for Uncertain Systems
When system uncertainty is caused by sudden, unpredictable and abrupt changes [37,112], then the 
and 
approaches may not be as efficient as the robust 
state estimation that provides peak‐to‐peak or 
‐to‐
filtering and prediction. Using the approach developed in Chapter for systems operating under disturbances, next we will develop more general 
‐to‐
FIR state estimators for uncertain systems operating under disturbances, initial errors, and measurement errors.
We will view the robust peak‐to‐peak FIR state estimation problem as minimization of the 
norm (8.178) of the induced 
represented by the ratio of the squared norms of the peak uncertainty 
and the peak error 
. Accordingly, we will determine the gain 
for this estimator by satisfying the cost function (8.180) represented as
where 
is a constant scalar and the minimum value of 
guarantees the gain suboptimality.
9.8.1 The a posteriori
‐to‐
FIR Filter
To develop an 
FIR filter for uncertain systems, we start with the familiar uncertainty‐to‐error state space model (9.244) and (9.245),
where the sparse matrices 
and 
are defined by (9.201), the matrix 
is given by (9.246) as
and all other definitions can be adopted from (9.238).
We next apply lemma 8.5 to (9.244) and (9.245), note that 
, and arrive at the following algorithm to compute a suboptimal gain 
for the robust 
‐to‐
a posteriori FIR filter.
Solve the minimization problem,
where the matrix 
is given by (9.274) and the sparse matrices 
and 
are defined by (9.201). The initialization should be started with 
. For the gain 
obtained by solving (9.275), the a posteriori 
‐to‐
FIR filtering estimate is computed by (9.248) and the error matrix by (9.249).
9.8.2 
‐to‐
FIR Predictor
Similarly, we develop the 
‐to‐
FIR predictor using the uncertainty‐to‐error state‐space model (9.268) and (9.269),
where the sparse matrices 
and 
are given by (9.201) and the matrices 
and 
are defined by (9.270) using the matrix 
defined by (9.266). The lemma 8.6 applied to the previous state‐space model finally gives the algorithm to numerically compute the suboptimal gain 
for the robust 
‐to‐
FIR predictor.
Solve the minimization problem,
starting the minimization with 
. Provided that 
is available from (9.276), the 
‐to‐
FIR prediction is computed by 
and the error matrix by (9.272).
We finally notice that all robust FIR algorithms developed in this chapter for uncertain systems can be modified to be bias‐constrained (suboptimally unbiased) if we remove the terms with 
and subject the LMI‐based algorithms to the unbiasedness constraint. That can be done similarly to the bias‐constrained suboptimal 
FIR state estimator. Moreover, all algorithms can be extended to general state‐space models with control inputs. It is also worth noting that all of the FIR predictors discussed in this chapter become the RH FIR filters needed for state feedback control by changing the time variable from 
to 
.
9.9 Summary
In this chapter, we have presented various types of robust FIR state estimators, which minimize estimation errors for maximized system uncertainties and other errors. Uncertainties in systems can occur naturally and artificially due to external and internal reasons, which sometimes lead to unpredictable changes in matrices. Since uncertainties cannot be described in terms of distributions and covariances, robust state estimators are required. To cope with such effects, robust methods assume that the undefined matrix increments have zero mean and are norm‐bounded. Because a robust FIR state estimation of uncertain systems must be performed in practice in the presence of possible disturbances, initial errors, and measurement errors, this approach is considered the most general. Its obvious advantage is that algorithms can be easily simplified for specific errors.
An efficient way to obtain robust FIR estimates is to reorganize the state‐space model by moving all components with undefined matrices into errors. This makes it possible to use the state‐space models previously created for disturbances, and the results obtained in Chapter can be largely extended to uncertain systems.
The errors in such estimators are multivariate, since their variables are not only undefined matrix components, but also disturbances, initial errors, data errors, and uncertain increments in the control signal matrix. In view of that, each error residual matrix acquires an additional increment, which depends on specific uncertain components. Accordingly, the error matrix of the FIR estimator is generally combined by six submatrices associated with disturbances, errors, and uncertainties.
As other FIR structures, FIR state estimators for uncertain systems can be developed to be bias‐constrained. This property is achieved by neglecting the terms with initial errors and embedding the unbiasedness constraint using the Lagrange method. Since the derivation procedure is the same for all FIR structures, we postponed the development of bias‐constrained FIR estimators for uncertain systems to “Problems”. Another useful observation can be made if we recall that the robust approach for uncertain systems has been developed in the transform domain. This means that by replacing 
with 
, all of the FIR predictors obtained in this chapter can easily be converted into the RH FIR predictive filters needed for state feedback control.
We finally notice that the algorithms presented in this chapter cover most of the robust FIR solutions available. However, higher robustness is achieved by introducing additional tuning factors, and efforts should be made to properly maximize uncertainties and other errors. Otherwise, the estimator performance can degrade dramatically.
9.10 Problems
- An uncertain system is represented by the discrete‐time state‐space model in (9.1) and (9.2),
where the uncertain matrices are modeled as
, 
, 
, 
, and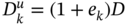 
. The known matrices 
, 
, 
, 
, and 
are constant, and the uncertain parameters 
, 
, 
, 
, and 
have zero mean and are norm‐bounded. Extend this model to 
and modify the 
FIR filtering algorithms. - Consider the following discrete‐time state‐space model with multiplicative noise components [56],
where
is a bounded disturbance and 
, 
, and 
are standard scalar white noise sequences with zero mean and the properties:
where
, 
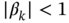, and 
and 
is the Kronecker delta. Convert this model to a more general model in (9.1) and (9.2) and modify the suboptimal FIR predictor. - An uncertain LTV system is represented by the following discrete‐time state‐space model [98]
where
is a bounded disturbance and 
, 
, 
, and 
are known time‐varying matrices such thatand
and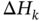 
are time‐varying parameter uncertainties obeying the following structurewhere
is an unknown real time‐varying matrix satisfying 
and 
and 
are known real constant matrices with appropriate dimensions. Note that this model is widely used in the design of robust recursive estimators for uncertain systems. Consider this model as a special case of the general model in (9.1) and (9.2) and show that the conditions (9.277) and (9.278) can be too strict in applications. Find a way to avoid these conditions. - The estimation error of an FIR filter is given by (9.43) as
where the residual error matrices
, 
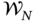, and 
are given by (8.15)–(8.17) and the uncertain residual matrices specified by (9.44)–(9.46). Taking notice that the a posteriori 
FIR filter is obtained in this chapter for 
, rederive this filter for 
. - Consider the
FIR filter (9.206), the gain 
for which is computed numerically using the algorithm in (9.203)–(9.205). Modify this algorithm for the estimate to be bias‐constrained and make corrections in the error matrix (9.207). - Solve the problem described in item 5 for the
FIR predictor and modify accordingly the inequalities (9.227)–(9.229) and the error matrix (9.231). - A Markov jump LTV uncertain system is represented with the following discrete‐rime state‐space model [228]
(9.279)
(9.280)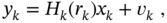
where
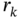is a discrete Markov chain taking values from a finite space 
with the transition probability 
for any 
. Matrices 
, 
, and 
are 
‐varying and the random sequences are white Gaussian, 
and 
. Transform this model to the general form (9.21) and (9.22), extend to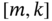 
, and develop an 
FIR predictor. - Consider the problem described in item 7 and derive the
, 
‐to‐
, and 
‐to‐
FIR predictors. - Given an uncertain system represented with the state‐space model
and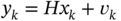 
, where the matrices are specified as
and
is an uncertain nonconstant time step. Suppose that 
has zero mean and is bounded. Derive the 
‐OFIR and 
‐OUFIR filters. - A harmonic model is given in discrete‐time state‐space with the following equations
and 
, where matrices are specified as
is a constant angle, 
is an undefined bounded scalar, 
, and 
and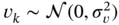 
are scalar white Gaussian sequences. Derive the 
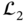‐to‐
and 
‐to‐
FIR predictors for this model. - An uncertain system is represented with the following discrete‐rime state‐space model
where
, 
, and 
and 
are undefined and uncorrelated norm‐bounded increments. Noise sequences 
, 
, and 
are white Gaussian. Convert this model to the general form (9.21) and (9.22), extend to 
, and develop an 
FIR predictor.
