Systematically solving rational equations

You can solve rational equations, such as , without as much hassle if you simply get rid of all the denominators. To do so, you work with an old friend, the least common denominator. The least common denominator (LCD) is also known as the least common multiple — the smallest number that two or more other numbers all divide into evenly (such as 2, 3, and 4 all dividing the LCD 12 evenly). Head to Chapter 18 for a quick trick on finding an LCD.

To solve this example equation with the LCD, you find a common denominator, write each fraction with that common denominator, and then multiply each side of the equation by that same denominator to get a nice quadratic equation (see Chapter 3 for a full discussion of quadratic equations).

Quadratic equations can have two solutions, so they present more opportunities for extraneous solutions. Be on the lookout!

1. Find a common denominator.

   The first step in solving the rational equation is to find the least common denominator (LCD) for all the terms in the equation.

   For example, the common denominator of all three fractions in the equation consists of the product of all the factors in the three denominators, .

   Each of the denominators has to be able to divide into the common denominator evenly. In other words, the LCD is a multiple of each of the original denominators. To solve this equation, is the common denominator, because it’s a multiple of 4 — you multiply by to get it; it’s a multiple of  — you multiply by 20 to get it; and it’s a multiple of 5 — you multiply by  to get it. All three denominators divide this product evenly.

2. Write each fraction with the common denominator.

   Multiply each of the terms in the original equation by some value so that, after the multiplication, each resulting term has the same denominator — the LCD you’re so fond of:

   

   The “some value” I speak of is equal to one, because each of the fractions multiplying the terms is the same in the numerator and denominator. But you carefully select the fractions that serve as multipliers — the numerators and denominators must consist of all the factors necessary to complete the LCD.

   You can just divide the LCD by the current denominator to determine what more you need to create the common denominator in that term.

   Now, multiplying each fraction and simplifying,

   

3. Multiply each side of the equation by that same denominator.

   Multiply each term in the equation by the least common denominator to reduce each term and get rid of the denominators:

   

   Now simplify what’s left.

   

   One pitfall of multiplying both sides of an equation by a variable is that you may have to multiply both sides by zero, which may introduce an extraneous solution. Be sure to check your answer in the original equation when you’re finished to make sure your answer doesn’t make one or more of the denominators equal to zero.

4. Solve the new equation.

   By completing the previous steps for this example problem, you produce a quadratic equation (if you don’t know what to do with those, turn to Chapter 3).

   To solve the new quadratic equation, you can either factor or use the quadratic formula. This equation factors into .

   After factoring, you set each factor equal to zero and solve for x. When , , and when , .

5. Check your answers to avoid extraneous solutions.

   You now have to check to be sure that both your solutions work in the original equation. As I discuss in the introduction to this section, one or both may be extraneous solutions.

   The most common indication that you have an extraneous solution is that you end up with a zero in the denominator after replacing all the variables with that answer. Occasionally, you get a “nonsense” equation such as when checking — and that tells you that the solution is extraneous — but those are very special cases. You should always check your answers after solving equations. Make sure that the value(s) you find create true statements.

   

   When replacing the x in the original equation with the two solutions, they both work.

   Rational equations don’t always work out so well, though. Take the equation , for example. If you work through Steps 1 through 4, you get a new equation:

   

   The solutions for this equation are and .

   When you try in the original equation, it works out:

   

   which becomes or .

   However, when you substitute into the original equation, you get

   

   which becomes .

   Stop right there! You can’t have a zero in the denominator. The solution works just fine in the quadratic equation, but it isn’t a solution of the rational equation; is extraneous.

Solving rational equations with proportions

A proportion is an equation in which one fraction is set equal to another.

For example, the equation is a proportion. Proportions have several very nice features that make them desirable to work with when you’re solving rational equations because you can eliminate the fractions or change them so that they feature better denominators. Also, they factor in four different ways.

When you have the proportion , the following are also true:

• ad and bc, the cross-products, are equal, giving you .
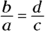• , the reciprocals, are equal (you can flip the proportion).

Reducing every which way but loose

Another wonderful feature of proportions is that you can reduce the fractions in a proportion by finding common factors in four different directions: top, bottom, left, and right. The ability to reduce a proportion comes in handy when you have large numbers in the equation.

Here are the rules for reducing proportions across the top (numerators), bottom (denominators), left, and right and an example for each:

Numerators	Denominators	Left	Right

The reduced forms of the proportions make cross-multiplication much easier and more manageable. Take the following proportion, for example. You first reduce across the numerators, and then you reduce the left fractions.

reduces or which reduces again which is then written .

Now cross multiply and solve the quadratic equation.

When , ; and when , . Both solutions check out.

Squaring both sides of a radical equation

If you have an equation in the form , you square both sides of the equation to get rid of the radical. The only problem arises when you end up with an extraneous root.

Consider the non-equation . You know that the equation isn’t correct, but what happens when you square both sides of this statement? You get , or . Now you have an equation. Squaring both sides can mask or hide an incorrect statement.

Much like the process of getting rid of fractions in equations, the method of squaring both sides is the easiest way to deal with radicals in equations. You just accept that you always have to watch for extraneous roots when solving equations by squaring.

For example, to solve the equation , follow these steps:

1. Change the equation so that the radical term is by itself on the left.

   In this case, you add 6 to each side of the equation.

   

2. Square both sides of the equation.

   becomes .

   A very common error when squaring problems is to square the binomial on the right incorrectly. Don’t forget the middle term — you can’t just square the two terms alone .

3. Simplify the result and solve the resulting equation.

   In this example, you have a quadratic equation (see Chapter 3). Set it equal to zero and solve it:

   

   When , . When , .

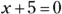4. Check to see whether your solutions fit with the original equation.

   Plug your answers in the original equation, 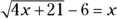. When ,

   

   It works. Checking , you get

   

   This solution works, too.

Both solutions working out is more the exception rather than the rule when you’re dealing with radicals. Most of the time, one solution or the other works, but not both. And, unfortunately, sometimes you go through all the calculations and find that neither solution works in the original equation. You get an answer, of course (that there is no answer), but it isn’t very fulfilling.

Calming two radicals

Some equations that contain radicals call for more than one application of squaring both sides. For example, you have to square both sides more than once when you can’t isolate a radical term by itself on one side of the equation. And you usually need to square both sides more than once when you have three terms in the equation — two of them with radicals.

For example, say you have to work with the equation . Here’s how you solve the problem:

1. Move the radicals so that only one appears on each side.
   
2. Square both sides of the equation.
   

   After simplifying the results of the first two steps, you have the following:

   

3. Move all the nonradical terms to the left and simplify.

   This gives you

   or

4. Make the job of squaring the binomial on the left easier by dividing each term by two — the common factor of all the terms on both sides.

   You end up with , which becomes .

5. Square both sides again, simplify, set the quadratic equal to zero, and solve for x.

   This process gives you the following:

   

   When , ; and when , .

6. Don’t forget to check each solution in the original equation:
   

   The solution works. The other solution, , doesn’t work in the equation. The number 34 is an extraneous solution.

Flipping negative exponents out of the picture

In general, negative exponents are easier to work with if they disappear. Yes, as wonderful as negative exponents are in the world of mathematics, solving equations that contain them is just easier if you change the format to positive exponents and fractions and then deal with solving the fractional equations (see the previous section).

For example, the equation has a fairly straightforward solution. You write the variable x in the denominator of a fraction and then solve for x. A nice way to solve for x is to write the 4 as a fraction, creating a proportion, and then cross-multiply (check out the aptly named “Using cross-products to solve a rational equation” section earlier in the chapter for the lowdown):

is written , which becomes or .

The process can get a bit dicey when you have more than one term with a negative exponent or when the negative exponent applies to more than one term. For instance, in the problem , you have to rewrite the equation, changing the terms with negative exponents into rational or fractional terms.

You then find the common denominator for the three fractions, which is the product of the three different denominators, . Next, you rewrite each fraction as an equivalent fraction with that common denominator, multiply through to get rid of all the denominators (whew!), and solve the resulting equation. Didn’t think you’d ever prefer to switch to fractions, did you?

When , ; and when , .

You can’t simplify by distributing the exponent or multiplying it out in any way. You have to rewrite the term as a fraction to get rid of the negative exponent.

Factoring out negatives to solve equations

Negative exponents don’t have to have the same power within a particular equation. In fact, it may be more common to have a mixture of powers in an equation. Here are two useful methods for solving equations with negative exponents:

• Factoring out a greatest common factor (GCF)
• Solving the equation as if it’s a quadratic (quadratic-like; see Chapter 3)

Solving quadratic-like trinomials

Trinomials are expressions with three terms, and if the terms are raised to the second degree, the expression is quadratic. You can simplify quadratic trinomials by factoring them into two binomial factors. (See Chapter 3 for details on factoring trinomials.)

Often, you can factor trinomials with negative powers into two binomials if they have the following pattern: . The exponents on the variables have to have a special arrangement, where one of the exponents is twice the other. For instance, the trinomial fits this description. Make this into an equation, and you can solve it by factoring and setting the two factors equal to zero:

When , and when .

You produce two solutions, and both work when substituted into the original equation. You haven’t changed the format of the equation, but you still have to be sure that you aren’t putting a zero in the denominator for an answer.

You need to be careful when solving an equation containing negative exponents that involves taking an even root (square root, fourth root, and so on). The following problem starts out behaving very nicely, factoring into two binomials:

The first factor offers no big surprise. You get two solutions after changing the negative exponent and solving the equation by using the square root rule (see Chapter 3 for more on this rule):

The other factor doesn’t have a real solution because you can’t find a square root of a negative number (in Chapter 3, you find more information on what happens when you try to take the square root of a negative number; in Chapter 14, you find out how to deal with imaginary numbers — those square roots of the negatives):

Look at all the possibilities — and ways to trip up with solutions. Watch out for zeros in the denominator, because those numbers don’t exist, and be wary of imaginary numbers — they exist somewhere, in some mathematician’s imagination. Factoring into binomials is a nifty way for solving equations with negative exponents; just be sure to proceed cautiously.

Combining terms with fractional exponents

Fortunately, the rules of exponents stay the same when the exponents are fractional:

• You can add or subtract terms with the same base and exponent: .
• You can multiply terms with the same base by adding their exponents: .
• You can divide terms with the same base by subtracting their exponents: .
• You can raise a fractional power to a power by multiplying the two powers: .

Fractional exponents may not look that much better than the radicals they represent, but can you imagine trying to simplify without changing the format? You can always refer to the second entry in the previous list to see how fractional powers make doing the multiplication possible.

Factoring fractional exponents

You can easily factor expressions that contain variables with fractional exponents if you know the rule for dividing numbers with the same base (see the previous section): Subtract their exponents. Of course, you have the challenge of finding common denominators when you subtract fractions. Other than that, it’s smooth sailing.

To factor the expression , for example, you note that the smaller of the two exponents is the fraction . Factor out x raised to that lower power, changing to a common denominator where necessary:

A good way to check your factoring work is to mentally distribute the first term through the terms in the parentheses to be sure that the product is what you started with.

Solving equations by working with fractional exponents

Fractional exponents represent radicals and powers, so when you can isolate a term with a fractional exponent, you can raise each side to an appropriate power to get rid of the exponent and eventually solve the equation. When you can’t isolate the fractional exponent, you must resort to other methods for solving equations, such as factoring.

Raising each side to a power

When you can isolate a term that has a fractional exponent attached to it, go for it. The goal is to make the exponent equal to 1 so you can solve the equation for x. You accomplish your goal by raising each side of the equation to a power that’s equal to the reciprocal of the fractional exponent.

For example, you solve the equation by raising each side of the equation to the power, because multiplying a number and its reciprocal always gives you a product of one:

giving you .

You finish the problem by evaluating the radical (see the section “Ridding Yourself of a Radical”):

The evaluation is easier if you take the fourth root first and then raise the answer to the third power. You can do this because powers and roots are on the same level in the order of operations (refer to Chapter 1 for more on this topic), so you can calculate them in either order — whatever is most convenient.

Factoring out variables with fractional exponents

You don’t always have the luxury of being able to raise each side of an equation to a power to get rid of the fractional exponents. Your next best plan of attack involves factoring out the variable with the smaller exponent and setting the two factors equal to zero.

To solve , for example, you first factor out an x with an exponent of :

Now you can set the two factors equal to zero and solve for x. When ; and when .

Factoring into the product of two binomials

Often, you can factor trinomials with fractional exponents into the product of two binomials. After the factoring, you set the two binomials equal to zero to determine if you can find any solutions.

To solve , for example, you first factor the trinomial into two binomials. The exponent of the first variable is twice that of the second, which should indicate to you that the trinomial has factoring potential. After you factor (see Chapter 3), you set the expression equal to zero and solve for x:

When ; and when . Check your answers in the original equation (see the fifth step in the section “Systematically solving rational equations” earlier in this chapter); you find that both and work.

Putting fractional and negative exponents together

This chapter wouldn’t be complete without an explanation of how you can combine fractional and negative exponents into one big equation. Creating this mega problem isn’t something you do just to see how exciting an equation can be. The following is an example of a situation that occurs in calculus problems. The derivative (a calculus process) has already been performed, and now you have to solve the equation. The hardest part of calculus is often the algebra, so I feel I should address this topic before you get to calculus.

The two terms in the equation have the common factor of . Notice that both terms have a power of x, a power of , and a power of in them. (You have to choose the lower of the powers on a factor and use that on the greatest common factor.)

Dividing each term by the greatest common factor (see the section “Factoring out a negative GCF” for more), the equation becomes

Now you simplify the terms inside the brackets:

You can set each of the four factors (the three in the greatest common factor and the fourth in the brackets) equal to zero to find any solutions for the equation (see Chapter 3):

When , . When . When . And, finally, when . The solutions you find are , , and . You see repeated roots, but I name each of them only once here. The trinomial that remains in the factorization, , doesn’t have any real solution when set equal to 0.